三轴电磁-压电混合驱动快速刀具伺服的轨迹跟踪控制
朱志远, 朱紫辉, 周晓勤, 朱利民, 朱志伟*
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.吉林大学 机械与航空航天工程学院,吉林 长春 130025;3.上海交通大学 机械与动力工程学院,上海 200240)
1 引 言
基于快速刀具伺服(Fast Tool Servo, FTS)的单点金刚石车削方法被广泛用于复杂光学曲面的超精密加工[1-3]。当前,FTS主要采用压电[2,4]、洛伦兹力[5]和电磁法应力[3,6]等进行驱动。其中,电磁法应力驱动由于具有较大行程和较高力密度等优点,近年来应用于数十至数百微米的中等行程FTS的驱动源[6]。
为实现法应力电磁驱动FTS刀具运动轨迹的超精密跟踪,CHEN等[3]基于理想Bode图频率整形,设计了分数阶控制系统。LU等[7]针对所研制的超快FTS,在主控制器基础上迭加了自适应前馈抵消控制器,以实现对拟周期性轨迹的超高精度跟踪。为抑制外部切削力的扰动,WU等[8]和房丰洲等[9]设计了自抗扰控制器(ADRC)用于电磁法应力驱动FTS的轨迹跟踪,通过扩张状态观测器(Extended State Observer, ESO)对系统未建模特性、非线性和未知扰动进行观测并补偿。夏薇等[10]采用扰动观测器(Disturbance Observer, DOB)对系统未建模和非线性部分进行观测补偿。然而,ESO和DOB有限的观测估计能力限制了轨迹跟踪性能的进一步提升。为补偿电磁驱动磁滞损耗引起的迟滞非线性,ZHANG等[11]构建了基于Duhem模型的系统迟滞模型,并对法应力电磁驱动纳米定位平台进行了前馈补偿以提高系统的控制精度。
相较于单轴FTS,三轴FTS可同步驱动金刚石刀具沿XYZ三轴进行超精密运动,更高的运动自由度赋予了三轴FTS更高的加工柔性,可实现复杂曲面的自适应加工需求[13-14]。当前三轴FTS仍以压电并联驱动为主,CHEN等[2]和ZHU等[12]采用三轴压电正交布置,分别设计获得了理论上运动解耦的三轴FTS,并将各轴视为相互独立的单输入单输出(Single-input-single-output,SISO)系统,采用PID控制器实现三轴轨迹跟踪控制。LI等[13]将三轴FTS视为SISO系统,采用Prandtl-Ishlinskii逆模型三轴压电进行开环补偿,并利用PID控制器对Z轴运动进行闭环控制。作者团队在前期研发了混合法应力电磁驱动和压电驱动的串并混联三轴FTS,其中法应力电磁驱动构成平面XY并联运动,而压电驱动串联搭载于平面运动上实现Z轴运动[14]。基于该构型原理,作者团队进一步优化结构参数制作了第二代样机,尽管三轴间具有理论解耦性,但加工装配等原因会引起轴间耦合,同时动力学耦合带来的高阶谐振等因素不可避免地会降低各轴的控制精度。
针对所研制的三轴电磁-压电混合驱动、串并联混合构型FTS的高精度轨迹跟踪控制问题,本文以陷波滤波器消除系统的高阶谐振来改善系统动力学性能,基于轴间耦合模型构建前馈解耦补偿,将三轴驱动转化为弱耦合SISO系统。最终,以PID为主控制器,并结合基于动态迟滞模型的前馈补偿实现三轴FTS对复杂空间轨迹的高精度跟踪。
2 三轴电磁-压电混合驱动FTS
2.1 三轴FTS驱动系统
三轴电磁-压电混合驱动FTS的结构剖视示意如图1(a)所示,主要包括二维XY平面并联法应力电磁驱动模块和串联搭载在平面驱动上的Z向压电驱动模块。平面驱动由四组完全对称的法应力单向驱动单元构成,其基本结构和驱动原理如图1(b)所示。其中,永磁铁在动子两侧的气隙内产生反向、恒定的偏置磁场,励磁线圈则在气隙内产生同向、可调的驱动磁场,偏置磁场和驱动磁场的叠加使得动子两侧产生大小不等的磁吸力,从而实现对动子的驱动。偏置磁场的引入使得驱动单元从理论上获得了线性相关于励磁电流和动子位置的驱动力。如图1(a)所示,通过对四组驱动单元进行正交对称布置,并采用类双平行柔性导向机构,实现了平面XY并联驱动的理论解耦。
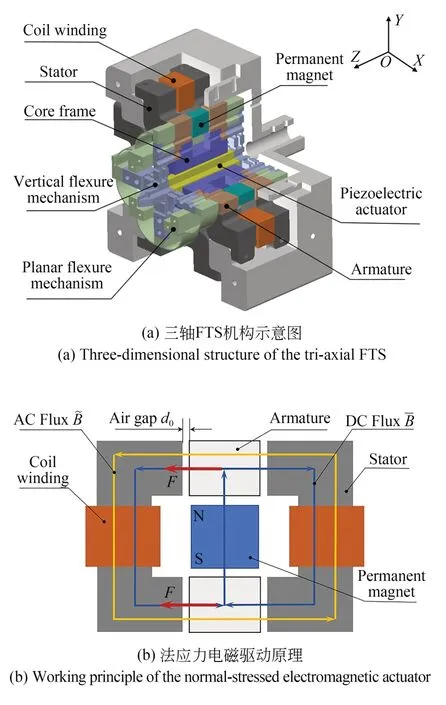
图1 三轴FTS结构与原理Fig.1 Schematic and principle of tri-axial FTS
这里基于直圆柔性铰链设计了交叉对称双平行柔性铰链机构,用于压电叠堆的Z向运动导向,并将该Z向驱动模块整体串联搭载在平面电磁驱动模块上,从而构建了三轴串并混联、电磁-压电混合驱动FTS。为弱化Z向压电驱动惯性力对平面运动的扰动,压电驱动采用相对XY平面对称的双向驱动方法。所设计的三轴FTS详细的结构描述和工作原理可参见文献[14],合理选择结构参数,FTS的XY轴向行程约为50 μm,Z轴行程约为15 μm。
2.2 FTS动力学测试
为测试系统动力学特性并辨识系统动力学模型,所搭建的测试系统照片如图2所示,相应仪器的型号与主要技术指标如表1所示。为测试三轴运动,采用三组Microsense公司生产的超精密电容位移传感器正交布置,并尽可能靠近刀尖位置以获得刀具实际运动,电容传感器的带宽和量程分别为20 kHz和500 μm。采用PCIe-6363型高性能数据采集卡在所配置的Desktop Real-time实时控制模式下,对测得的位移信号进行采集,并实时计算控制量输出信号以实现对FTS运动的控制,在测试过程中设置的采样频率为20 kHz。采集卡实时输出的平面XY运动控制量经过两个SMA5005-1型线性伺服功率放大器放大后驱动励磁线圈,而Z向运动控制量则经过E-617.001型功率放大器驱动压电叠堆。

表1 FTS动力学测试实验仪器及其性能指标Tab.1 Instrumentations and their performance for dynamics testing of FTS
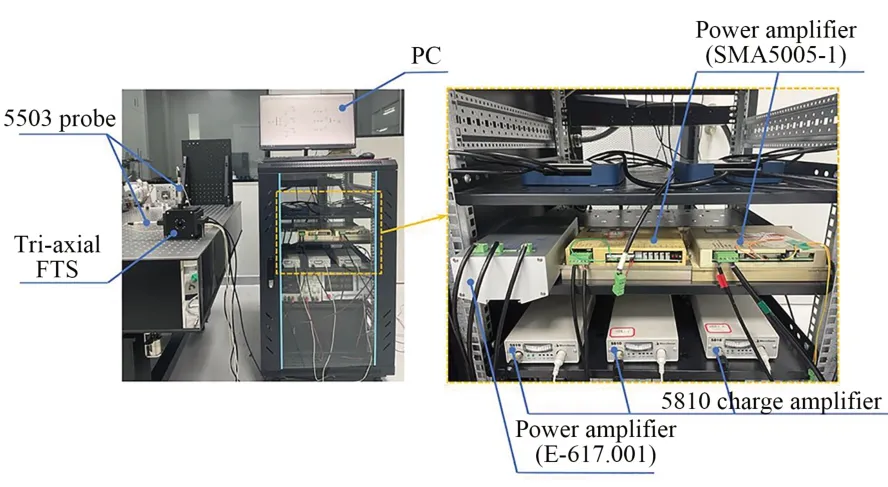
图2 FTS动力学测试系统实物图Fig.2 Photograph of experiment setup for FTS dynamic testing
为了测试三轴FTS的动力学特性,对每个运动轴分别进行扫频激励。平面XY轴扫频电压幅值设为0.25 V,频率从0.1 Hz线性变化至1.5 kHz;Z轴的扫频电压幅值和偏置电压均设为1 V,频率从0.1 Hz线性变化至6 kHz。对输入命令信号和输出位移信号进行快速傅里叶变换,并通过比较输入输出的幅值比和相位差,获得三轴的频率响应函数,如图3所示。由图3可知,X轴运动存在两个频率为490 Hz和690 Hz的谐振峰;Y轴运动只有1个谐振峰,所对应的谐振频率为564 Hz;Z轴运动有3个谐振峰,对应的谐振频率分别为1 331,1 501,2 872 Hz。
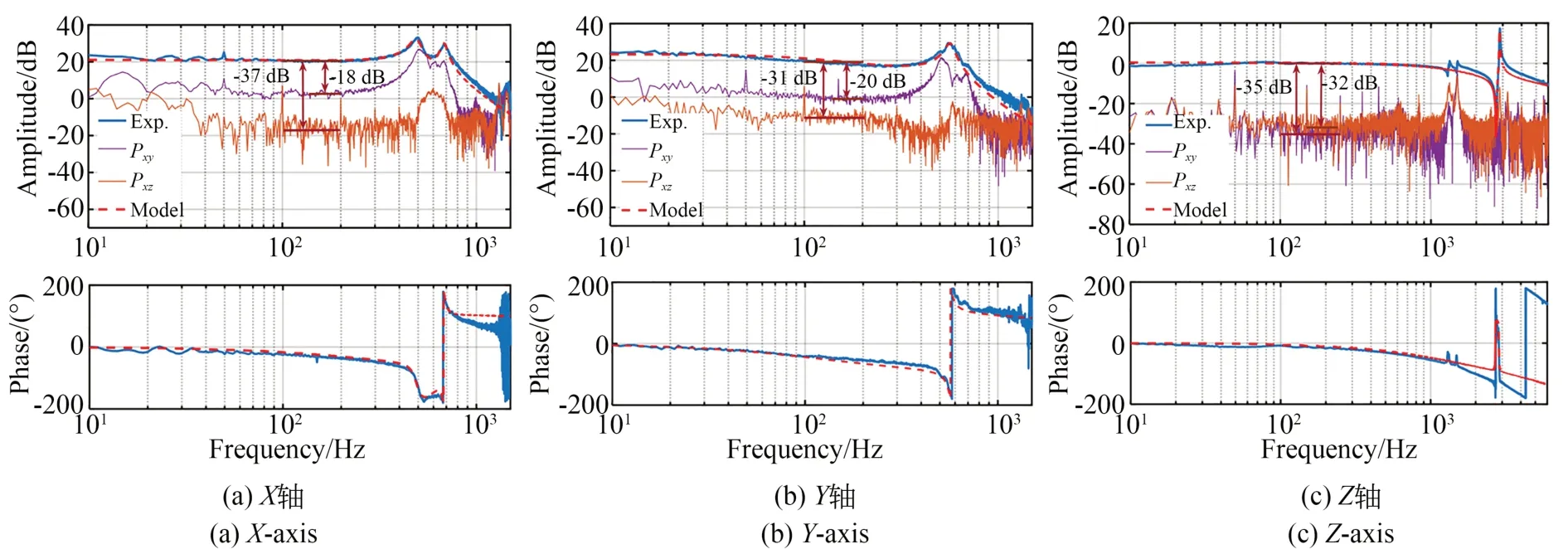
图3 三轴FTS的开环频率响应函数Fig.3 Open-loop frequency response functions of tri-axial FTS
从耦合频率响应函数可知:X轴对Y和Z轴的动态耦合Pxy,Pxz的幅值分别比主运动响应Pxx小18 dB和37 dB;Y轴对X和Z轴的动态耦合Pyx,Pyz的幅值分别比主运动响应Pyy小20 dB和31 dB;Z轴对平面XY轴的动态耦合Pzx,Pzy的幅值分别比主运动响应Pzz小35 dB和32 dB。由此可知,尽管三轴FTS具有理论运动解耦性,但是加工、装配误差等仍会引入轴间耦合运动。其中,XY平面并联运动间的轴间耦合较大,而串联于XY平面运动上的Z轴运动对平面耦合较小,对FTS整体的运动精度影响较小。
考虑各轴的谐振特征,辨识获得的各轴名义传递函数分别为:
由名义模型生成的频率响应函数也绘制在图3中,与实验测试结果具有很好的吻合度,这表明所辨识的系统模型能够较为准确地描述三轴FTS的动力学特性,可以用于设计控制系统。
3 高性能轨迹跟踪控制系统设计
由动力学测试结果可知,三轴FTS的XZ轴存在高频谐振,这会降低系统运动的稳定性,而XY轴间还存在着较大的运动耦合,这会降低平面运动精度。针对该问题,这里采用陷波滤波器对X轴和Z轴的高频谐振进行动力学补偿,并以前馈解耦补偿降低XY平面的运动轴间耦合,从而综合改善系统的动力学特性。
另一方面,电磁驱动固有的磁滞损耗和压电内摩擦导致的能量耗散等不可避免地会在三轴运动中引入迟滞非线性,从而恶化运动精度。针对该系统非线性,本文以动力学补偿后的线性模型级联静态Prandtl-Ishlinskii迟滞模型构建各轴动态非线性模型,并基于相邻时间步各参量近似相等的假设,构建无需直接求逆的迟滞前馈补偿模型,从而改善被控系统的运动特性。以经典的PID为主控制器,所构建的三轴FTS控制系统框图如图4所示,其中Hi-1(i=x,y,z)为动态迟滞逆模型,Nxy(s),Nyx(s)为设计的解耦器,Rk(t)(k=x,y,z)为系统的输入,j(t)(j=x,y,z)为系统的输出。

图4 三轴FTS轨迹跟踪控制系统框图Fig.4 Block diagram of trajectory tracking control system for triaxial FTS
3.1 陷波滤波器设计
由图3可以看出,X轴在690 Hz处存在二阶谐振峰,Z轴在1 331,1 501和2 872 Hz处存在谐振峰,这类谐振峰会使系统在轨迹跟踪时出现抖振现象,从而影响跟踪精度。本文采用陷波滤波器以消除谐振峰影响,并尽可能地减少相位延迟。对于i=x,z方向,陷波滤波器可表示为[15]:
式中:对于X轴,k=1;对于Z轴,k=3,ωi,n,k和ωi,d,k为滤波器的中心频率,ξi,n,k和ξi,d,k为等效阻尼比,gi为滤波器的增益,一般取gi=针对被控系统,滤波器的中心频率根据XZ轴频率响应函数中的谐振频率获得,而阻尼比则通过试错法获得,最终所设计的陷波滤波器参数如表2所示。
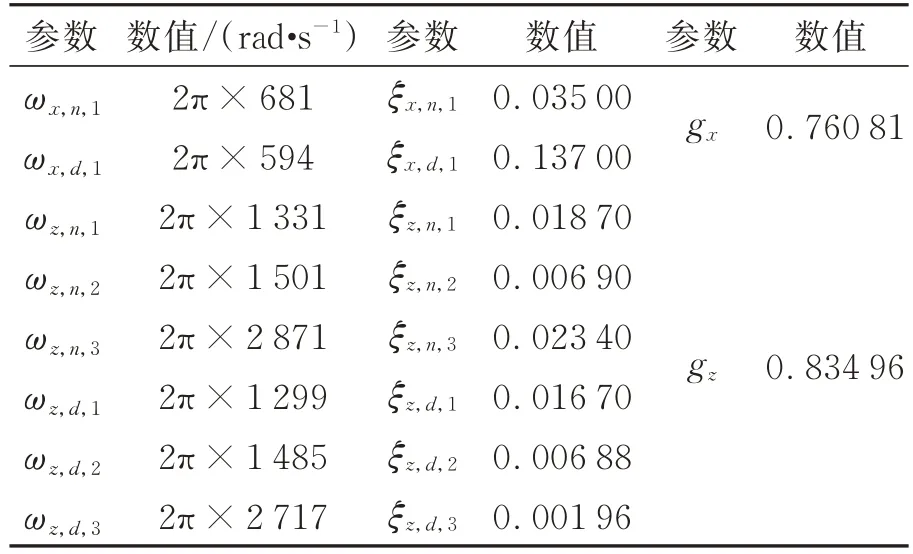
表2 陷波滤波器参数Tab.2 Parameters of notch filters
针对陷波修正后的系统,重新扫频测试获得的X轴和Z轴的频率响应函数分别如图5(a)和5(b)所示。陷波补偿后系统的高频谐振得到明显抑制,由于高频谐振引起的相位突变也得到了很好的补偿。采用三阶模型对陷波后的X轴和Z轴进行系统辨识,所获得的名义模型为:
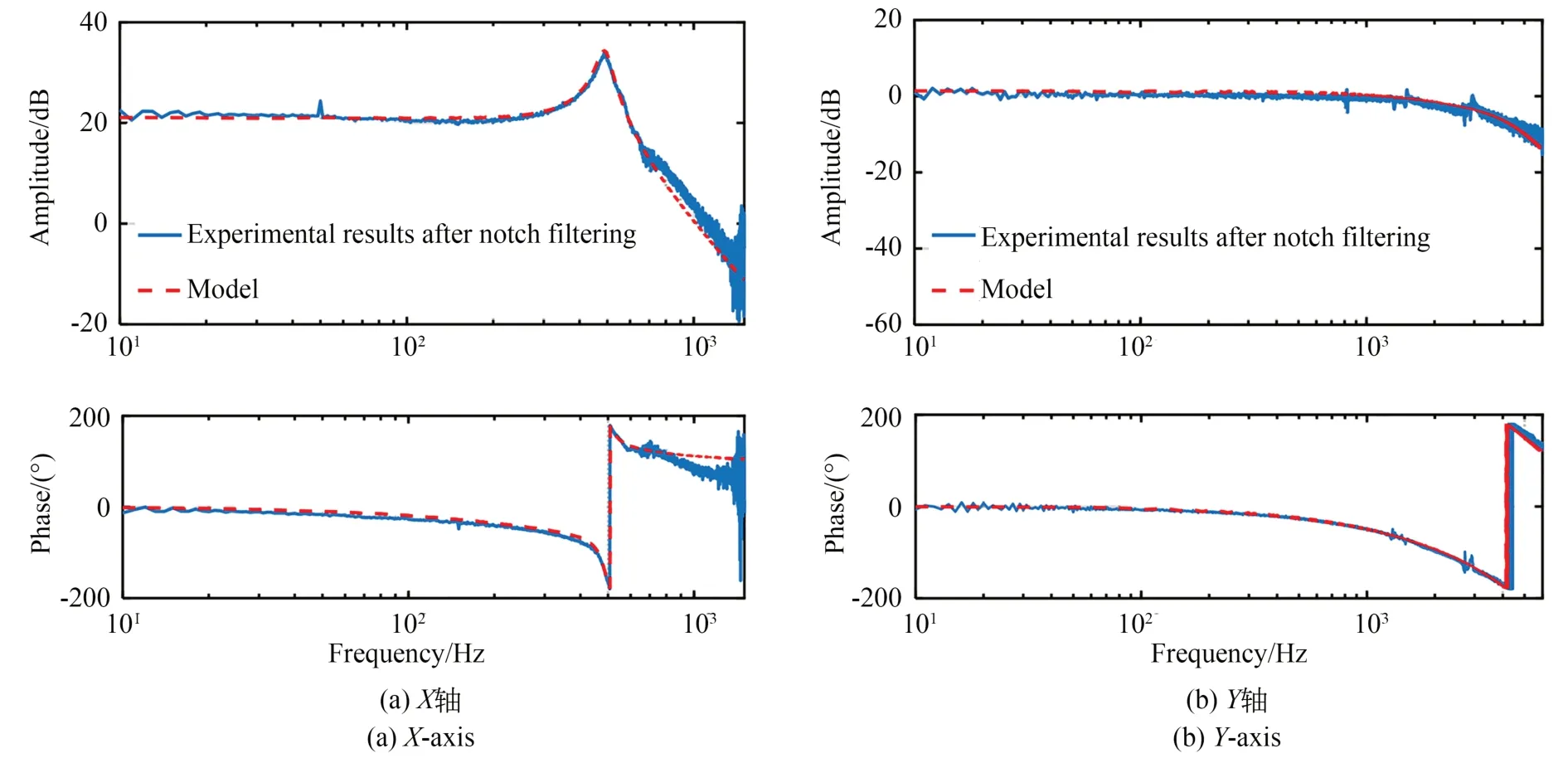
图5 系统陷波后的开环频率响应函数Fig.5 Open-loop frequency response function of triaxial FTS after notch filtering
图5给出了所辨识名义模型频率响应函数,能够很好地吻合实验测试结果,表明经过动力学改善后FTS各轴可近似描述为典型三阶系统。
3.2 前馈解耦补偿
前馈解耦补偿的基本原理是让某一轴向的输入对其他轴向输出的传递函数为零,从而实现轴间运动的解耦[16]。由2.2节三轴FTS动力学分析可知,平面XY向电磁驱动轴间耦合远大于Z向压电驱动引起的耦合。为简化控制系统,仅对平面强耦合运动进行解耦补偿,其前馈解耦补偿原理如图6所示,其中,ud,i(s)(i=x,y)为解耦系统输入,j(s)(j=x,y)为解耦系统输出。
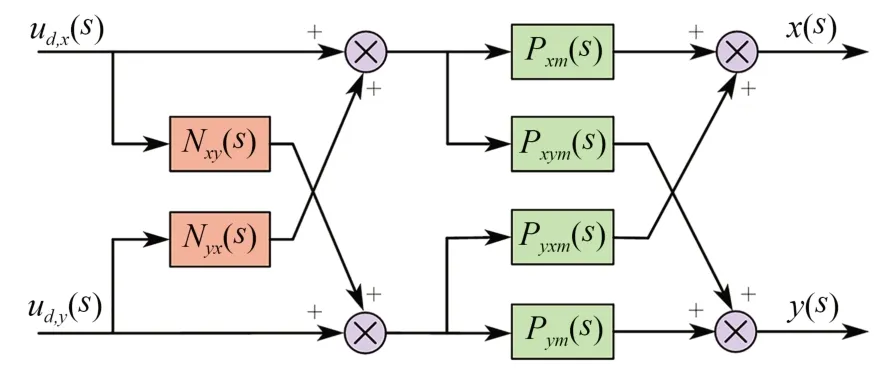
图6 平面运动前馈解耦补偿原理Fig.6 Principle for in-plane feed-forward decoupling
由图6可知,要实现平面运动的解耦,需要ud,x(s)对y(s)的传递函数和ud,y(s)对x(s)的传递函数均为零,即:
求解可得:
为获得Pxym(s)和Pyxm(s),对经陷波滤波补偿后的平面XY两轴进行扫频测试,所获得的轴间耦合频率响应函数如图7所示。考虑幅频响应特征,分别采用五阶和七阶传递函数进行耦合传递函数拟合,所辨识获得的两轴耦合传递函数Pxym(s)和Pyxm(s)为:
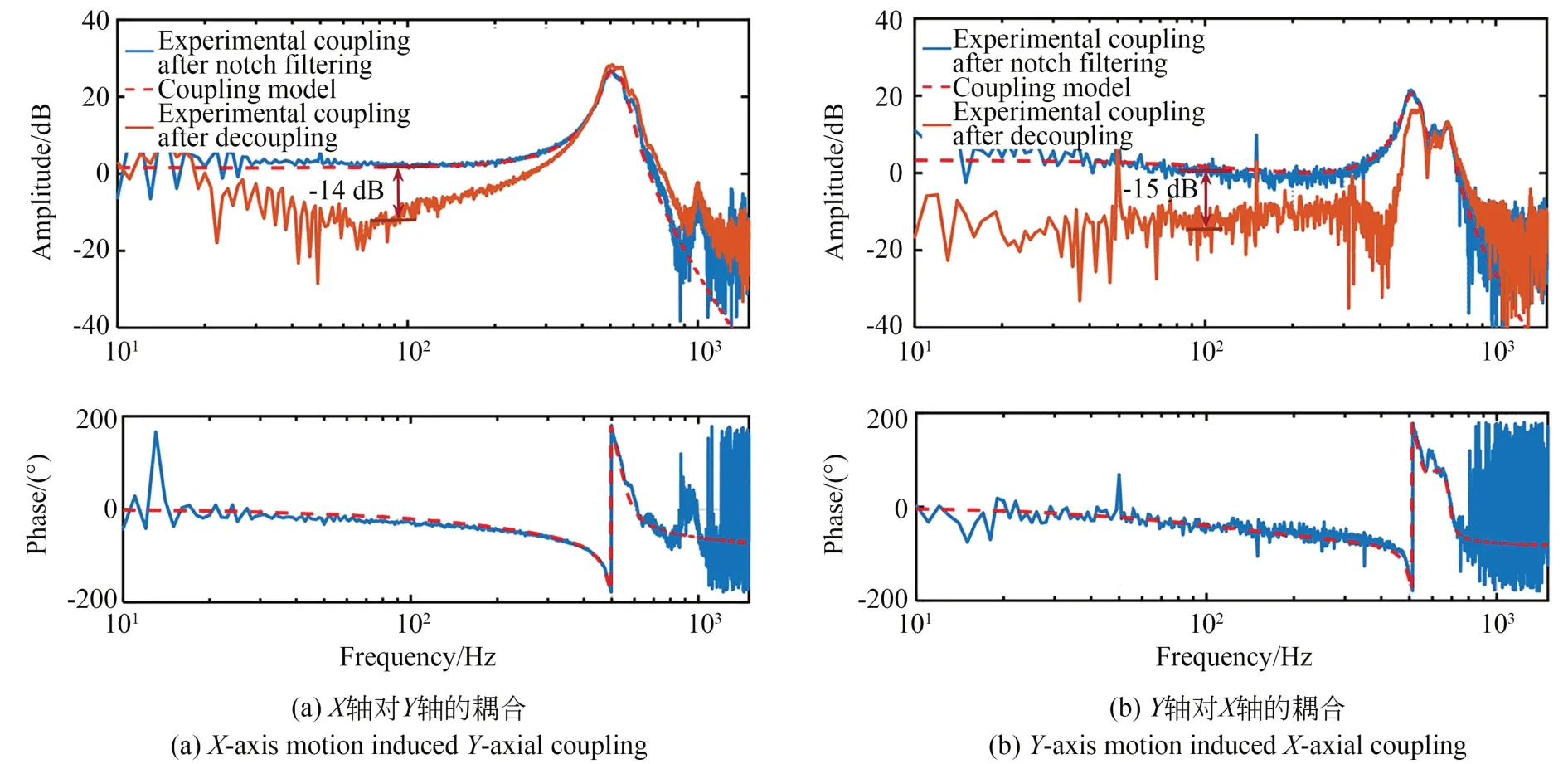
图7 陷波补偿后平面耦合频域响应函数Fig.7 Frequency response functions of in-plane couplings after notch filtering
由所辨识模型Pxym(s)和Pyxm(s)获得的频率响应特性如图7所示,均能很好地吻合实际测试结果。值得指出的是,根据辨识结果由式(8)求解获得的解耦补偿控制器阶数较高,这会增加求解的复杂度并降低求解的稳定性。为了简化计算,在此采用静态增益代替解耦补偿控制器传递函数,以实现平面XY轴间的耦合补偿,即:
对经过解耦补偿后的系统进行扫频测试,重新获得X轴和Y轴的轴间耦合频率响应函数,如图7所示。与补偿前相比,轴间耦合分别降低了约14 dB和15 dB,证明了所构建的前馈解耦补偿方法的有效性。与主运动相比,补偿后X轴对Y轴的耦合约为-32 dB,Y轴对X轴的耦合约为-35 dB,从而将三轴运动视为相互独立的三个单输入单输出系统。
3.3 动态迟滞补偿
为补偿法应力电磁驱动和压电驱动存在的动态迟滞非线性,这里提出采用陷波补偿和解耦补偿后的线性动力学模型级联PI迟滞模型以描述系统的迟滞非线性,并构建等效补偿策略以提高三轴控制精度。
3.3.1 动态迟滞模型构建
基于线性迟滞算子的PI模型可表示为[17]:
式中:hk(uk)为PI模型的输出位移,uk为输入电压,pri,k(uk)和μi,k分别为第i个迟滞算子和其对应的权重系数,Ts为采样周期,li,k和ri,k分别为第i个迟滞算子的左右阈值。为了兼顾迟滞模型精度和计算复杂度,取算子个数N=8。
为了提高模型精度,算子的阈值需根据输入的变化而变化,为简化计算,阈值取为[18]:
式中:cm,k为非对称阈值修正系数,‖uk‖∞为控制电压的最大值,对于平面XY轴,‖ux‖∞=‖uy‖∞=4,对于Z轴,‖uz‖∞=10。
对于PI模型与系统动力学模型级联构建的动态迟滞模型,其驱动电压uk(t)与输出位移zk(t)的关系为:
式中:*表示卷积运算,L-1{·}表示Laplace逆运算。
3.3.2 PI模型参数辨识
动态迟滞模型的辨识实际上就是求解迟滞算子权重μi,k和阈值修正系数cm,k,可转换为以下函数最小化问题:
式中zk,d(tj)为与uk对应的FTS实测位移。
选取频率成分为1,10,20,50和100 Hz的谐波叠加信号作为三个轴的驱动电压,各谐波分量的幅值随机选取,用于辨识动态迟滞模型。选取典型遗传算法求解式(15)中最小化问题,参数边界根据经验选择为[-2,2],优化后的参数结果如表3所示。同时,所辨识模型的输出结果和实际测得的XYZ三向运动如图8(a)、8(b)和8(c)所示,两者表现出较好的一致性。由图8可知,XY两轴的模型误差小于±0.6 μm,分别约为满幅行程的±1.95%和±2.05%,Z轴的模型误差小于±0.13 μm,约为满幅行程的±1.73%,由此表明所辨识的模型能够很好地描述三轴FTS的迟滞非线性特性。

表3 XYZ三轴的迟滞模型参数Tab.3 Parameters of hysteresis models for XYZ axes
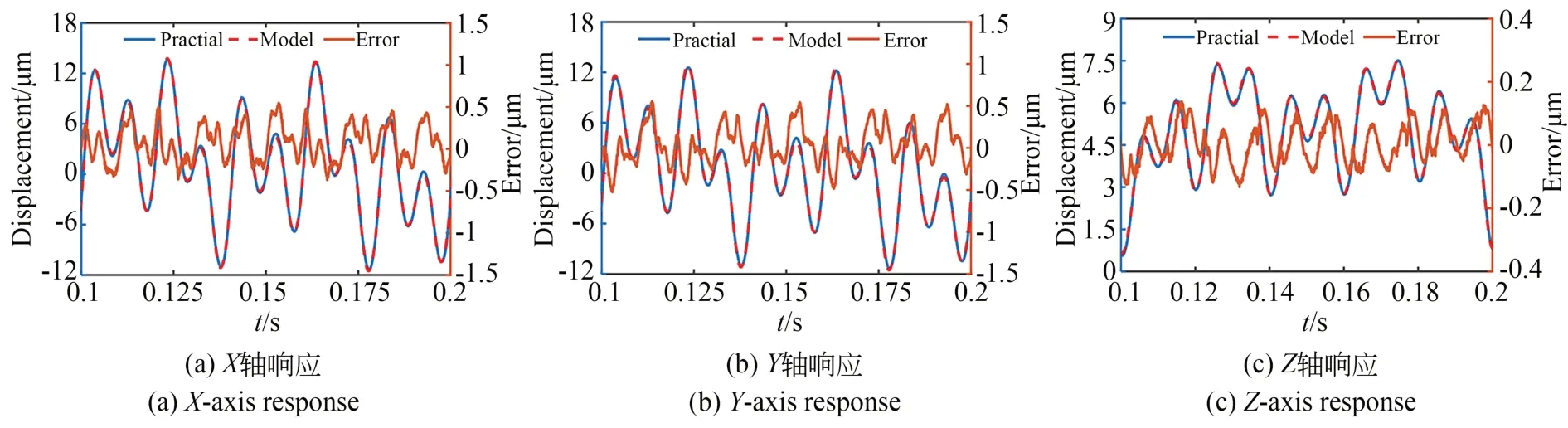
图8 动态迟滞模型的辨识结果Fig.8 Identification results of dynamic hysteresis model
为了验证所辨识模型的准确性,采用另一组频率成分不同的谐波叠加信号作为各轴驱动,XYZ三轴模型的预测结果和实际测试位移分别如图9(a)、9(b)和9(c)所示,X轴和Y轴的模型误差小于±0.8 μm,分别约为满幅行程的±2.14%和±2.17%,Z轴的模型误差小于±0.2 μm,约为满幅行程的±1.7%,进一步验证了所构建模型对不同驱动响应描述的准确性。
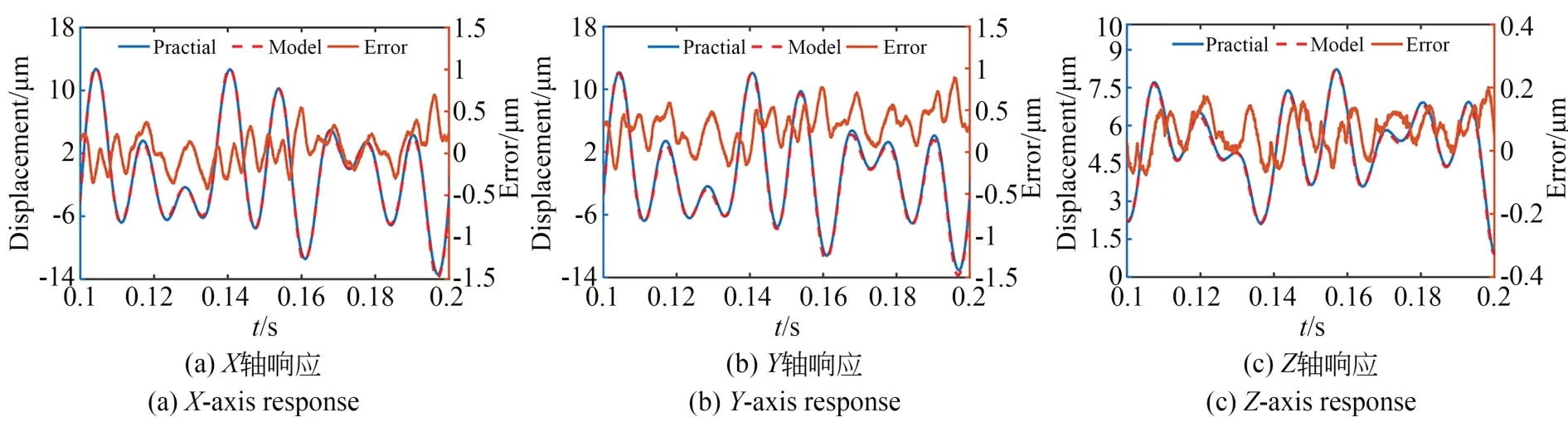
图9 动态迟滞模型验证结果Fig.9 Verification results of dynamic hysteresis model
值得指出的是,Z轴迟滞模型误差均小于平面电磁驱动的迟滞模型。这是由于与压电驱动相比,平面电磁驱动还存在铁磁材料响应非线性和漏磁非线性等多种复杂非线性因素,会影响建模精度。
3.3.3 迟滞前馈补偿
为避免求解非线性PI迟滞模型的逆,在此采用文献[19]中的近似方法求解等效迟滞逆补偿模型,如图10所示。假设对于任意k=x, y, z方向的期望轨迹Rk(t),在任意相邻两个采样时刻的迟滞模型输出和控制电压相等,即hk(uk(t))=hk(uk(t-Ts)),uk(t)=uk(t-Ts)。则式(16)可改写为[19-20]:

图10 动态迟滞等效逆补偿模型Fig.10 Equivalent inversion-based hysteresis compensation
3.4 PID控制
采用经典PID控制器作为FTS各轴运动的主控器,其传递函数可表示为:
式中:Kp,Ki,Kd和N分别为PID控制器的比例系数、积分系数、微分系数以及滤波器系数。
基于各轴动力学和轴间耦合补偿后的名义模型Pkm(s),k=x,y,z,以开环控制系统相位裕度不小于45°为约束,以截止频率尽可能大为目标优化获得各轴的PID控制器参数,如表4所示。
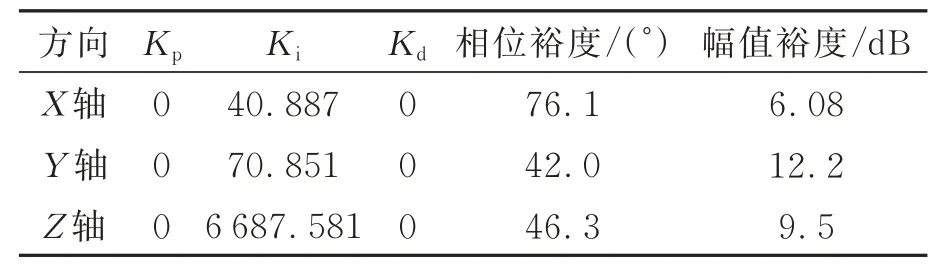
表4 XYZ三轴PID控制器参数Tab.4 PID parameters for XYZ axes
4 轨迹跟踪测试
4.1 基本跟踪性能测试
为验证轴间耦合补偿和迟滞非线性补偿的有效性,选取频率从10 Hz线性变化到100 Hz的谐波扫频信号作为期望轨迹。对于XY轴电磁驱动,期望轨迹的幅值为12 μm,而Z轴压电驱动的期望轨迹幅值和偏置均为3.5 μm。为进行验证比较,以PID迭加逆动力学前馈补偿达到的轨迹跟踪结果作为基准(PID+FF),分别以PID迭加动态迟滞补偿(PID+Hi-1)和PID迭加动态迟滞补偿和解耦补偿(PID+Hi-1+FD)的控制结果与之进行比较,以验证补偿策略的有效性。
采用三种控制策略的XYZ三轴轨迹跟踪结果分别如图11(a)、11(b)和11(c)所示,而三轴跟踪误差(实际位移与期望轨迹之间的差值)如图11(d)、11(e)和11(f)所示。由图 11可知,与单独的逆动力学前馈补偿相比,采用迟滞补偿后XYZ三轴的轨迹跟踪吻合度均有所提高,这也表现为该宽频范围内跟踪误差的降低。进一步迭加轴间耦合补偿后(PID+Hi-1+FD),平面XY轴的轨迹跟踪误差进一步降低。对于Z轴驱动,由于未进行耦合补偿,轨迹跟踪误差变化不明显,如图11(f)所示。
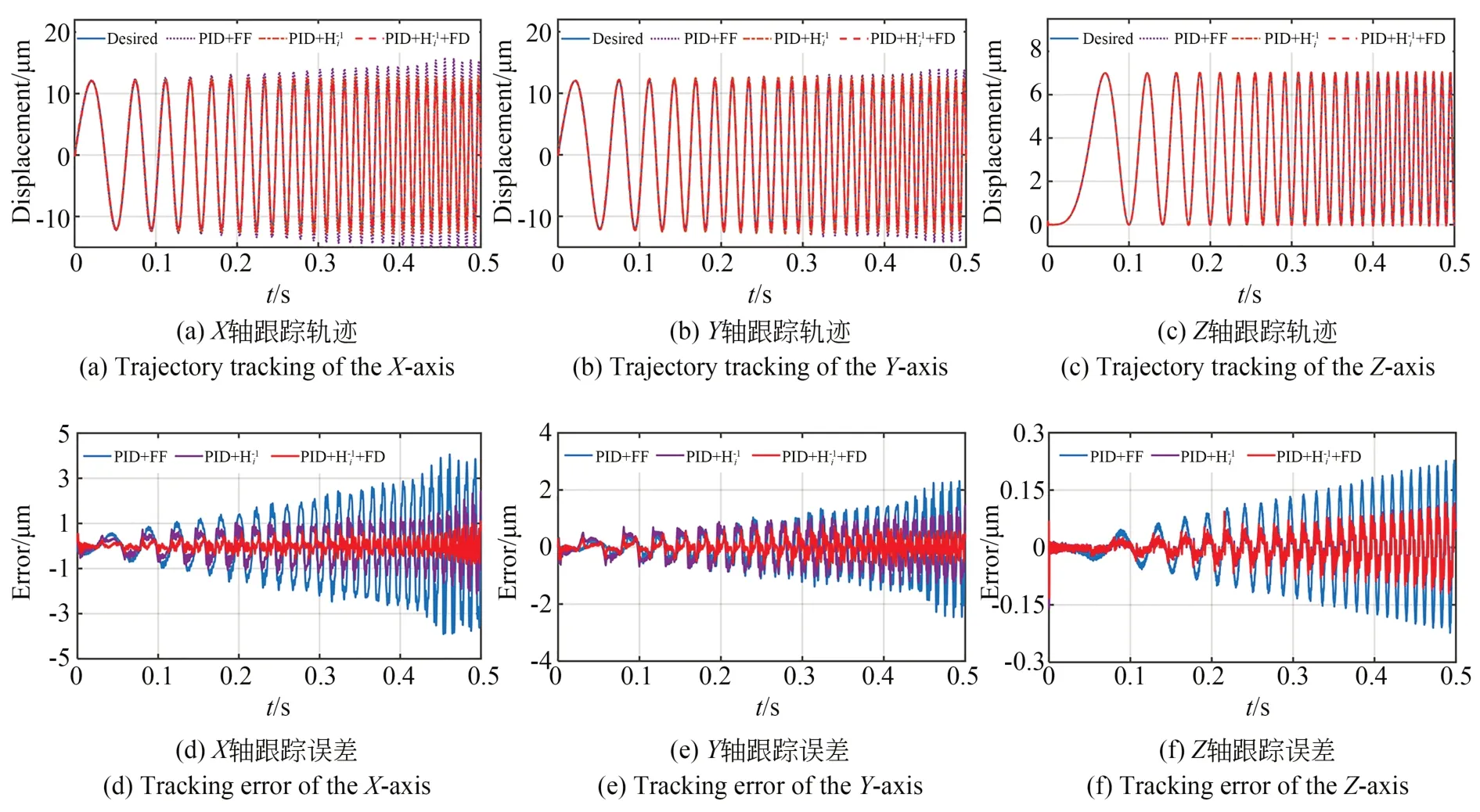
图11 复杂轨迹跟踪测试Fig.11 Complex trajectory tracking results
进一步,采用相对最大跟踪误差em和均方根误差erms量化表征轨迹跟踪误差,分别定义为:
式中:yd(t)为期望轨迹,ya(t)为实测轨迹,T为跟踪轨迹的周期。
误差统计结果如表5所示。由表5可知,X轴在进行动态迟滞补偿和解耦补偿后,最大轨迹跟踪误差em分别约为仅采用逆动力学补偿和仅采用迟滞补偿的26.7%和45.1%;Y轴在进行动态迟滞补偿和解耦补偿后,最大轨迹跟踪误差em分别约为仅采用逆动力学补偿和仅采用迟滞补偿的31.1%和53.2%;XY采用解耦补偿对Z轴轨迹跟踪的影响较小,采用迟滞补偿后最大跟踪误差约为逆动力学补偿系统误差的52.2%。对于均方根误差erms,各轴的轨迹跟踪误差变化规律与最大跟踪误差em近似一致,验证了所采用综合补偿策略的有效性。

表5 不同控制系统的跟踪误差Tab.5 Tracking errors of different control systems
4.2 空间轨迹跟踪
为了进一步验证所设计系统的三轴联动控制性能,对空间复杂螺旋球面轨迹进行了跟踪测试,螺旋球面轨迹的各轴运动为:
对该轨迹的空间跟踪结果和XYZ三轴跟踪误差分别如图12(a)和图12(b)所示,XYZ三轴的最大跟踪误差分别约为±0.63 μm,±0.60 μm和±0.012 μm,约为最大行程的±2.45%,±2.30%和±0.15%。结果表明,所设计的三轴控制系统能够同步跟踪空间复杂轨迹。
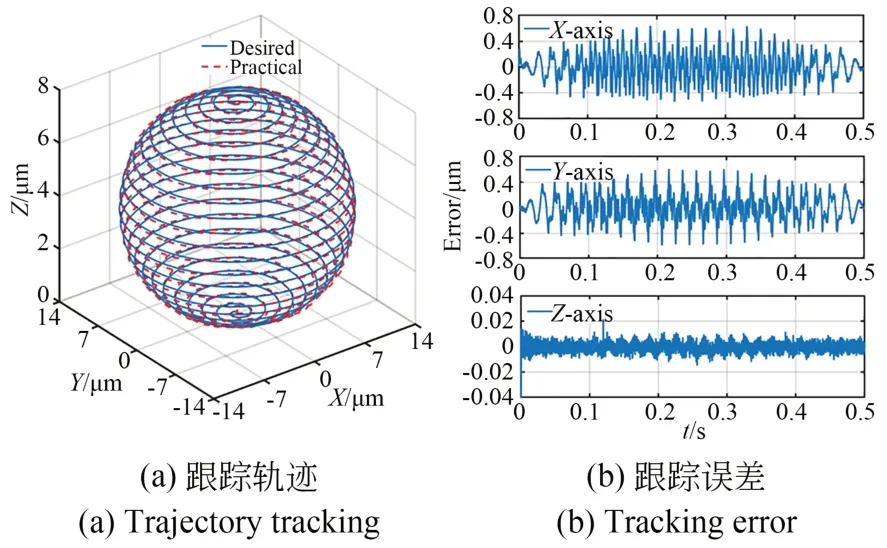
图12 空间轨迹跟踪Fig.12 Spatial trajectory tracking
5 结 论
本文针对三轴电磁-压电混合驱动FTS的高性能轨迹跟踪问题,采用陷波滤波器抑制系统的高频谐振,以基于耦合模型的前馈解耦补偿对XY平面并联运动间的强耦合进行补偿,使得补偿后的平面XY轴间运动耦合比补偿前分别降低了约14 dB和15 dB,最终X轴和Y轴获得了比主运动分别小约32 dB和35 dB的低耦合量。针对动力学谐振抑制和解耦改善后的三轴被控系统,采用动力学模型级联Prandtl-Ishlinskii模型对各轴动态迟滞进行描述,XY平面法应力电磁驱动和Z轴压电驱动的建模误差分别小于±2.20%和±1.8%。
以PID控制为主控制器,对性能改善后的各轴进行轨迹跟踪控制。基于动态迟滞逆模型构建了无需求逆的前馈补偿控制器,对系统非线性进行补偿控制,并对宽频谐波信号进行跟踪测试。对比实验结果表明,采用综合补偿策略获得各轴的最大跟踪误差约为仅采用逆动力学前馈补偿的25%至50%,最后对空间复杂轨迹进行了跟踪测试,获得的XYZ三轴跟踪误差分别约为最大行程的±2.45%,±2.30%和±0.15%,验证了所设计的控制系统的有效性。

