伞降航天器无损回收系统中地面网状回收平台控制研究

方文, 滕海山, 孙青林, 孙昊, 陈增强

(1.南开大学 人工智能学院, 天津 300350; 2.北京空间机电研究所, 北京 100094)

近年来,随着航天技术的不断提高,航天器的成本成为民用航天发展的绊脚石,如今航天器造价昂贵,而且均为一次性使用,高昂的价格使得很多公司对航天望而却步,因此,为了解决运载火箭的造价高昂的问题,使一次性的火箭变成重复性使用,提高航天器的回收效率,达到航天器无损回收的效果[1-4]。

针对航天器回收问题,文献[5-10]分析了国内外的航天器回收方法。常见的航天器的回收方法为控制航天器的运动轨迹,使航天器能够投放到某一个固定区域。虽然这种方法可以用网接住,降低航天器着陆时的冲击力,但是难以精准地将航天器投放到某一固定点。而马斯克团队在2020年8月19日采用海上无人船回收了部分火箭整流罩,没有考虑环境因素的影响[5],SpaceX使用的猎鹰9火箭整流罩回收船就是在一艘船上使用回收网来接住整流罩,但是接住的地点位于海面,所以一艘回收船就足已完成回收任务[6],我国的火箭发射平台大多是在内陆[7],所以需要4辆无人车拉着一张网构成一个地面网状回收平台对伞翼航天器进行回收,而SpaceX利用无人船上的网来回收整流罩成功的案例也证明了利用回收网进行伞翼航天器回收方案的可行性。地面网状回收平台根据不同的地理环境可以做出不同的反应,而且回收平台所拉起的网的面积理论上可以远远大于单一无人船所张开网的面积。在编队运动过程中,4辆无人车在陆地上的运动速度以及遇到障碍物进行避障的效率要远远高于无人船在海上的运动速度。

针对多车控制,使用PID算法对编队进行控制,使得机器人跟随领航者运动[11]。使用PI控制算法实现编队的控制,并且在编队控制的基础上提出了一种基于图和势场法的多车道护航编队自动驾驶方法[12]。PID算法的优点在于控制算法设计简单,适应性强,具有较强的鲁棒性,但不易调节到最优解。自抗扰控制(auto disturbance resistant control,ADRC)控制策略在传统的PID控制策略上做了一定的改进,具有参数易于调节,更强的鲁棒性等优点[13]。文献[14-17]提出了基于动物群体社会性行为机制的控制算法。同时文献[18-20]对编队一致性的问题进行了研究,使得在没有组织者和协调者的情况下,使各个智能体的状态达到一致。针对智能体避障过程,文献[21-22]分别使用人工势场法以及遗传算法进行避障控制。

通过对航天器回收方法的对比分析,本文提出了一种控制地面网状回收平台对伞降航天器进行无损回收的方法。将无人车编队问题与轨迹跟踪问题,无人车自主避障问题相结合,使用ADRC算法控制编队的形状以及无人车之间的距离保持一致,采取人工势场法完成无人车自主避障问题。

1 地面网状回收平台模型

对于领导者伞降航天器来说,其运动学模型只与自身的位姿信息有关,而作为地面网状回收平台的跟随者无人车的运动学模型则与领导者的位姿信息有关,通过与领导者之间的位置误差以及运动角度误差调整自身的位姿信息。

1.1 领航者运动模型

如图1所示,假定翼伞在某一时刻的位置为P=(vi,wi),vi和wi分别为翼伞的速度与角速度,且速度方向与水平方向之间的夹角为θi,则翼伞的位姿信息为Pi=(xi,yi,θi),而其运动信息为qi=(vi,wi)。相应的公式为:

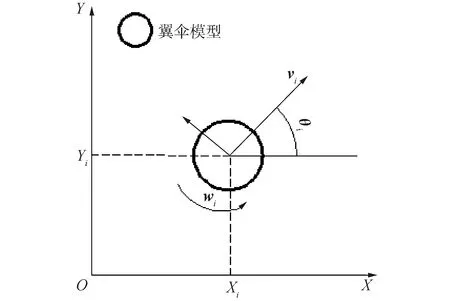
图1 领航者运动模型Fig.1 Navigator motion model

(1)

1.2 跟随者运动模型

无人车在本文中作为跟随者跟随领航者翼伞进行运动。图2为无人车-翼伞的编队模型,该模型由4个无人车(跟随者)以及1个翼伞(领航者)组成,箭头表示它们之间的通信拓扑。一组领导-跟随系统由图3所示。

图2 无人车-翼伞编队模型Fig.2 Unmanned vehicle-parafoil formation model

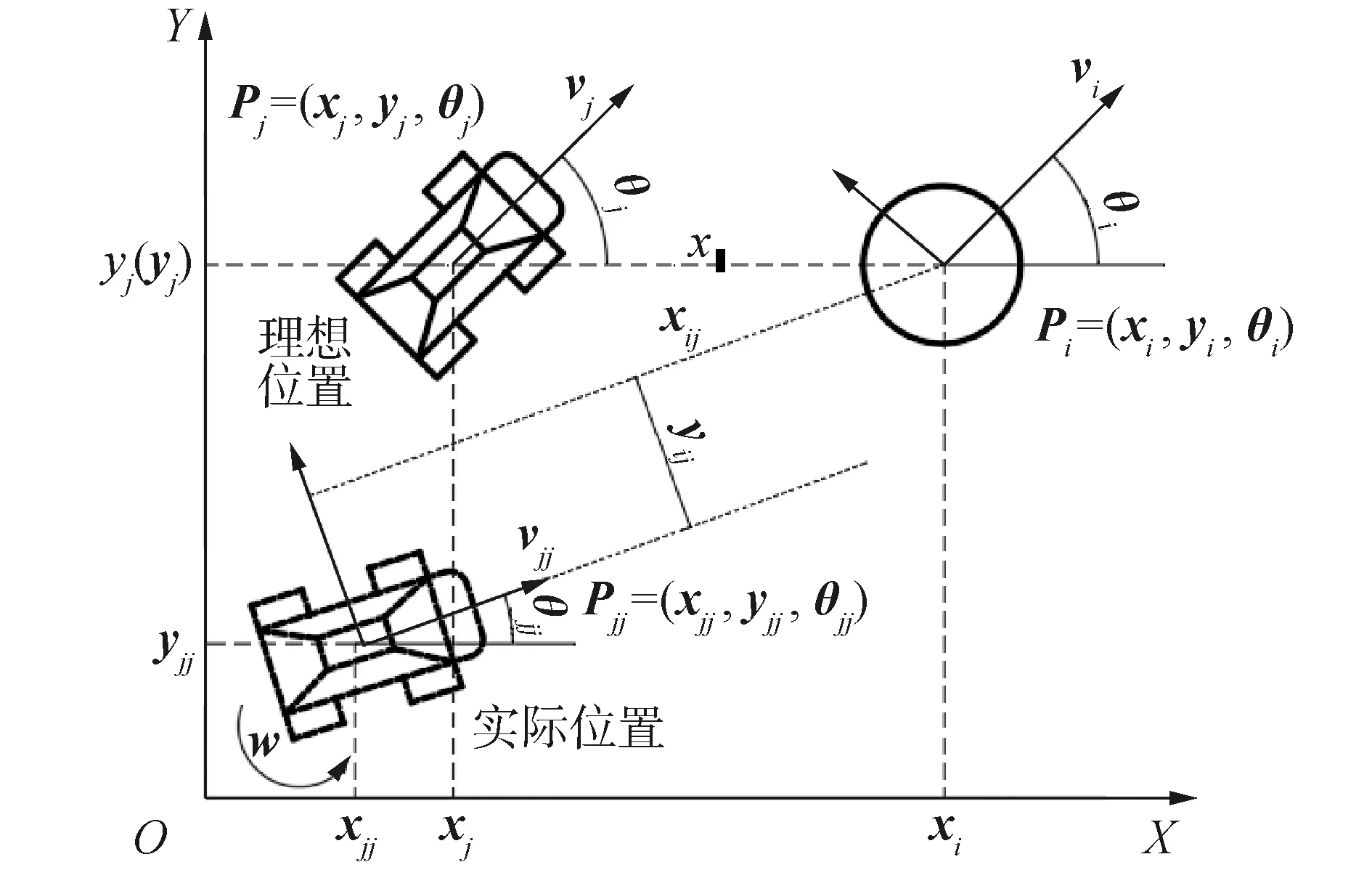
图3 领导-跟随系统运动模型Fig.3 Leader follower system motion model

图3中显示了无人车4与翼伞的运动模型,它们的预定位置信息可以分别用,Pj=(xj,yj,θj),Pi=(xi,yi,θi)表示,其中(xj,yj),(xi,yi)分别表示无人车j以及翼伞i在坐标系中的横坐标与纵坐标,θj与θi代表它们与水平方向的夹角。而Pjj=(xjj,yjj,θjj),Pi=(xi,yi,θi)分别代表无人车4和翼伞的实际位姿信息Pj=(xj,yj,θj)代表着无人车4的预定位姿信息。因此可以将无人车4与伞的实际位置误差q为:

(2)

而预定的位置误差可以设为:

(3)

式中qd分别表示无人车4与翼伞之间的预定位置误差。当无人车4与翼伞的位置误差未到达预定值时会根据算法促使它们达到预定值。而当它们达到预定值时无人车j的速度大小、方向以及角速度都会与翼伞相同,并且在没有遇到障碍物的情况下保持不变,以此来实现编队的稳定性。

1.3 回收网

回收网是地面网状回收平台的重要组成部分,承担起了回收伞翼航天器的功能,所以回收网的安装以及选择对整个回收过程至关重要。

市面上卖的回收网多采用维纶和尼龙等合成化纤作网绳,质量一般不超过15 kg,可承受800 N的冲击力。而本文系统的伞降航天器的质量大约为15 kg左右,在空中完成任务降落时,在着地之前翼伞已经对其进行减速,冲击力在回收网所能承受的范围内。当伞降航天器被回收网接住的瞬间,回收网必然会有一定的形变,智能车本身高0.3 m,在每个智能车上安装连接杆约0.5 m,可提高智能车的稳定性,做为回收网的支架,网与地面的最远距离0.8 m。通过调节回收网在连接杆上位置,改变回收网在小车的着力点和重心,确保不同质量的伞降航天器被接住时回收网所产生的形变不会接触到地面。此外试验场地一般为较为平坦的草地,高度起伏变化并不大,若是前后2车的高度起伏超过0.5 m对回收网的状态产生影响。

接住航天器后,上位机控制智能车编队由自动变为手动遥控运行,因此回收网接住伞翼航天器之后的情况不会对之前的结果产生影响,在伞降航天器落入回收网之前的算法也并不需要根据接住之后的状态进行改写,因此,回收网接住伞降航天器的状态并不会对本文研究结果产生较大的影响。

2 跟随领航者控制算法

对于领航者,给定固定的路线使其沿着这条路线到达目标点,而对于一个跟随者,则需要通过实时控制与领航者以及其他跟随者的位置误差控制速度及位置从而实现跟随领航者,达到与其他智能体形成编队的目的[23]。对于障碍物,需要利用人工势场法使跟随者进行避障,并且在避障过程结束之后能够快速恢复原来的阵型,从而做到地面网状回收平台在遇到障碍物能够自主避障,最终到达伞降航天器的正下方将伞降航天器接住,实现无损回收的目的。

2.1 通信拓扑

如图4所示,1、2、3、4分别为编队中的4个跟随者(无人车),5为领航者(即伞降航天器),箭头表示信息流方向,如Aij代表着信息从j流向i,Aij=1代表着j对i有信息交流,Aij=0则说明j对i没有信息交流。

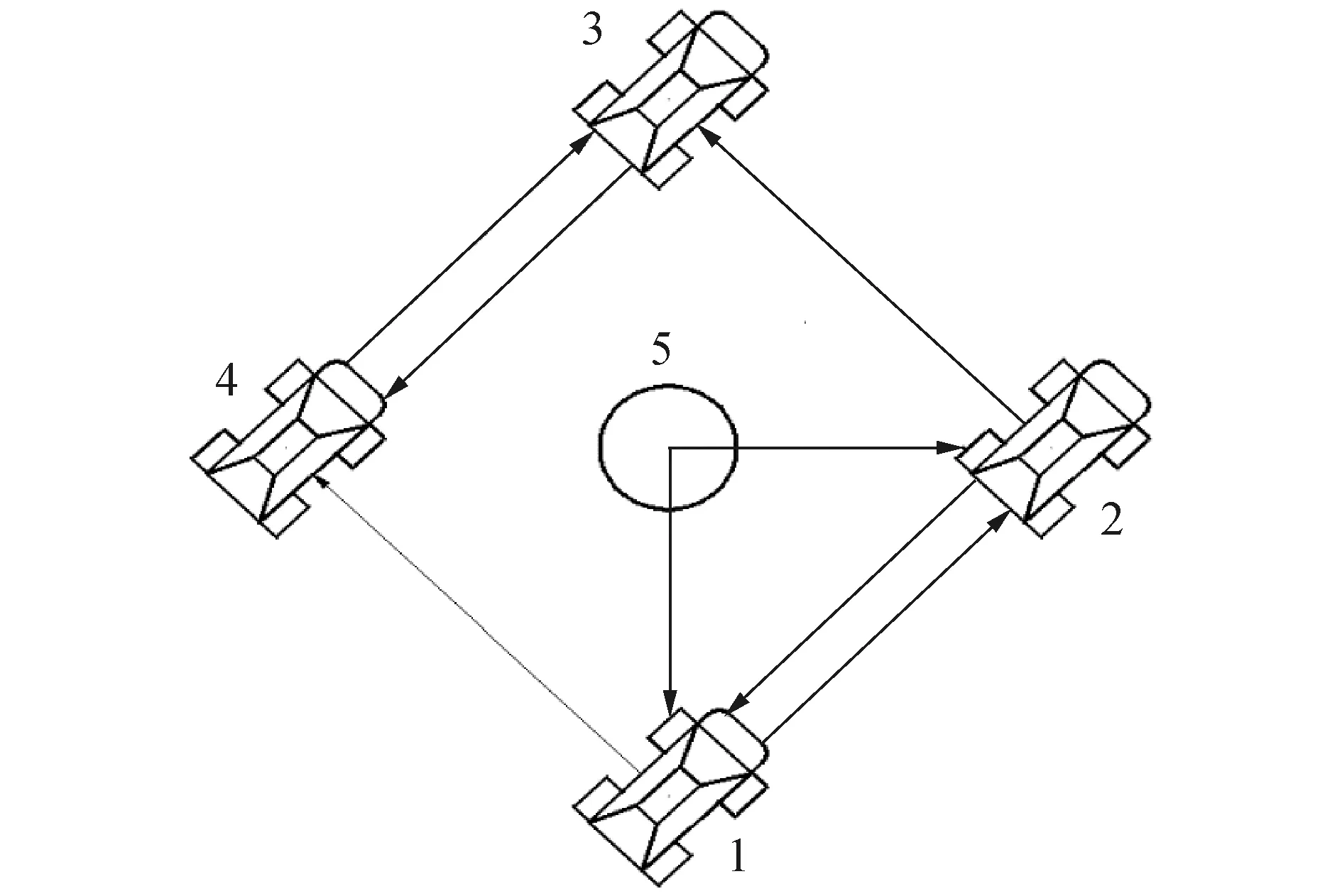
图4 通信拓扑图Fig.4 Communication topology

图4稳定的通信拓扑矩阵Aij为:

(4)

2.2 人工势场法

人工势场法作为路径规划算法中广泛应用的一种算法将物体的运动空间看成是一个虚拟的势场[24-26],障碍物和目标点会对一定范围内的物体产生斥力和引力从而达到使物体避障的效果[26-27]。如图5所示,单独考虑一个无人车受到的斥力,其中三角形为障碍物。

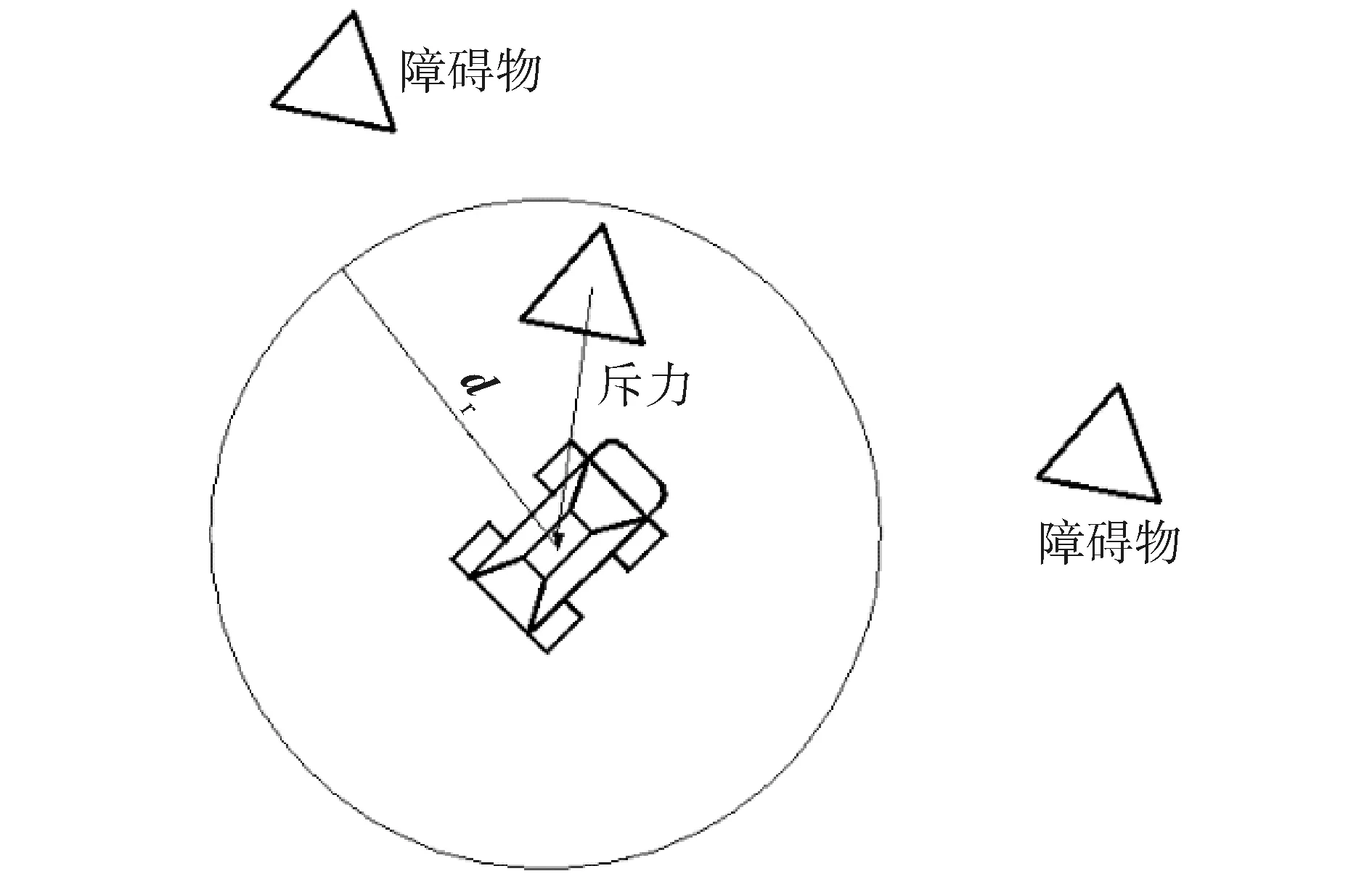
图5 人工势场Fig.5 Artificial potential field

在障碍物一定的圆形范围内,障碍物会对无人车产生一个朝向无人车的斥力,斥力场为:

(5)

式中:U为斥力大小;d为无人车与障碍物之间的离;dr为每个障碍物的影响半径。

为了防止无人车一直受到障碍物的斥力从而导致无法达到稳定状态,当无人车与障碍物之间的距离大于影响半径时障碍物对小车的斥力变为0。

2.3 自抗扰控制

传统的PID控制算法利用跟随者之间的相对距离误差来作为控制反馈,求出控制量u的值来对无人车进行控制。该方法基于误差进行控制,只要有位置误差,就会往无限逼近误差为零的方向调节。控制算法为:

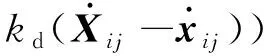
(6)

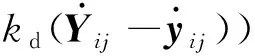
(7)

传统PID算法虽然设计简单,适应性强,需要调节的参数也不多,为调节参数的过程达到最优解,本文采用自抗扰控制算法对编队进行调节。自抗扰控制技术主要分为:非线性跟踪微分器(TD)、扩张状态观测器(ESO)及非线性反馈[28]。

在数字控制器中应用ADRC算法,需要对扩张状态观测器进行离散化。本文利用零阶保持器进行离散化,离散化后的二阶系统的a扩张状态离散空间表达式为:

(8)

Z(k)=[z1(k)z2(k)z3(k)]T

(9)

(10)

式中:z1(k)为观测的位置误差值;y(k)为实际输出值;e(k)为观测误差;z2(k)为观测位置误差导数值;z3(k)为观测到的系统总扰动。

根据输入信号和输入信号的微分与状态观测器观测到的系统输出和输出的导数的误差,进而进行控制和扰动补偿非线性反馈模块。

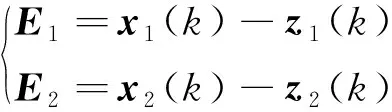
(11)

(12)

式中:x1(k)为预测位置误差输入;x2(k)为预测位置误差导数输入。它们分别与扩张状态观测器给出的状态变量估计z1(k),z2(k)相减,分别形成状态变量误差E1,E2。在式(11)中E1,E2与扩张状态观测器对未知作用力估计的补偿量z3(k)一起组成控制量u。

3 自适应算法仿真与结果分析

3.1 理想情况的仿真结果

为验证ADRC算法的可行性以及路径规划的效果,利用Matlab软件对理想情况进行仿真,在仿真过程中,将翼伞视为一个圆点,4辆无人车视为4个星号, 终点为三角形。分别对受传统PID算法和ADRC算法控制的编队在有障碍物的环境中形成编队,并进行避障。避障完成后重新组成编队验证ADRC算法的优越性。图6、7分别为PID与ADRC算法的编队路径,图8、9分别为2种算法的情况下跟随者与领航者之间的误差曲线。

图6 PID算法理想编队路径Fig.6 Ideal formation path of PID algorithms

图7 ADRC算法理想编队路径Fig.7 Ideal formation path of ADRC algorithms

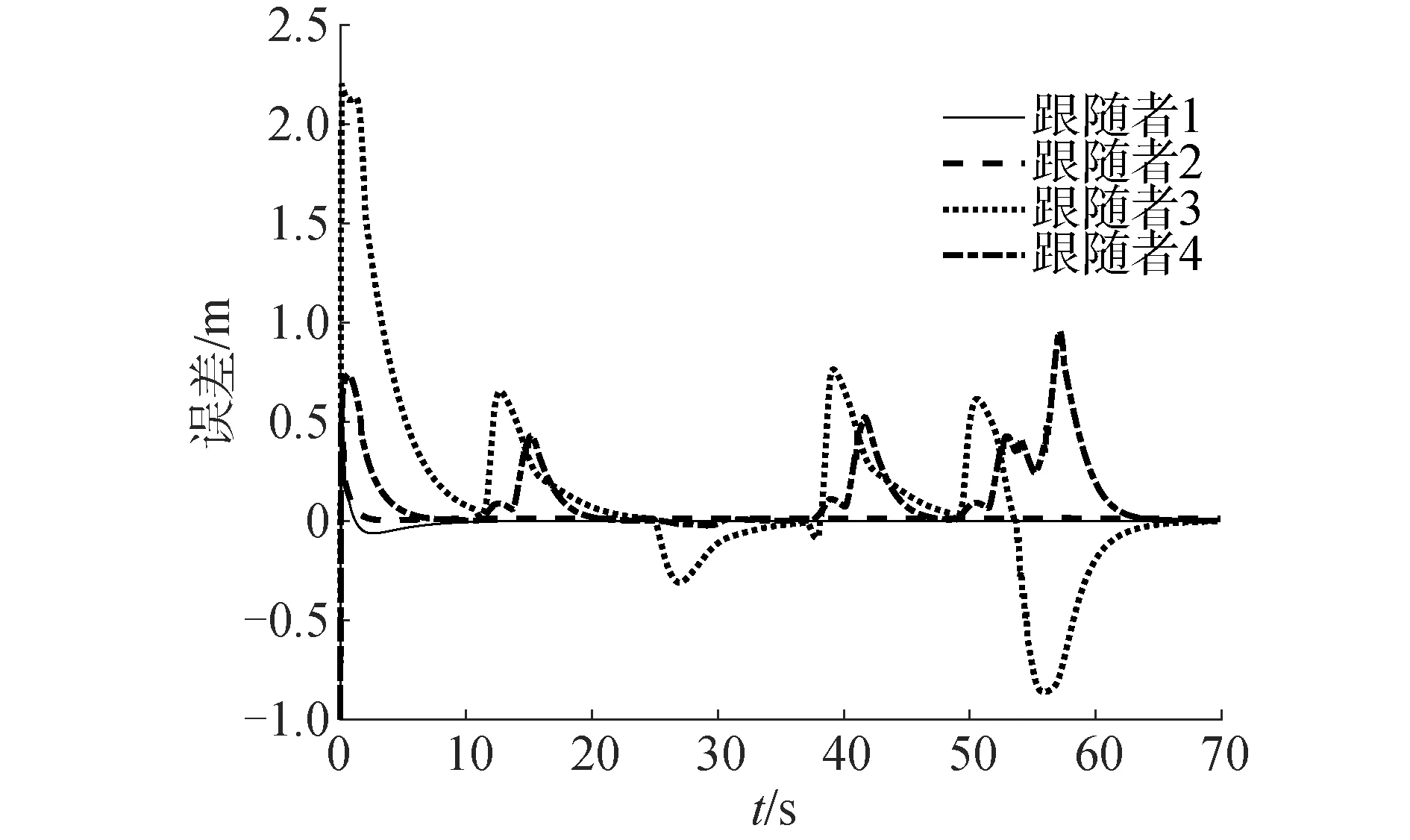
图8 PID算法理想误差曲线Fig.8 Ideal error curves of PID algorithms

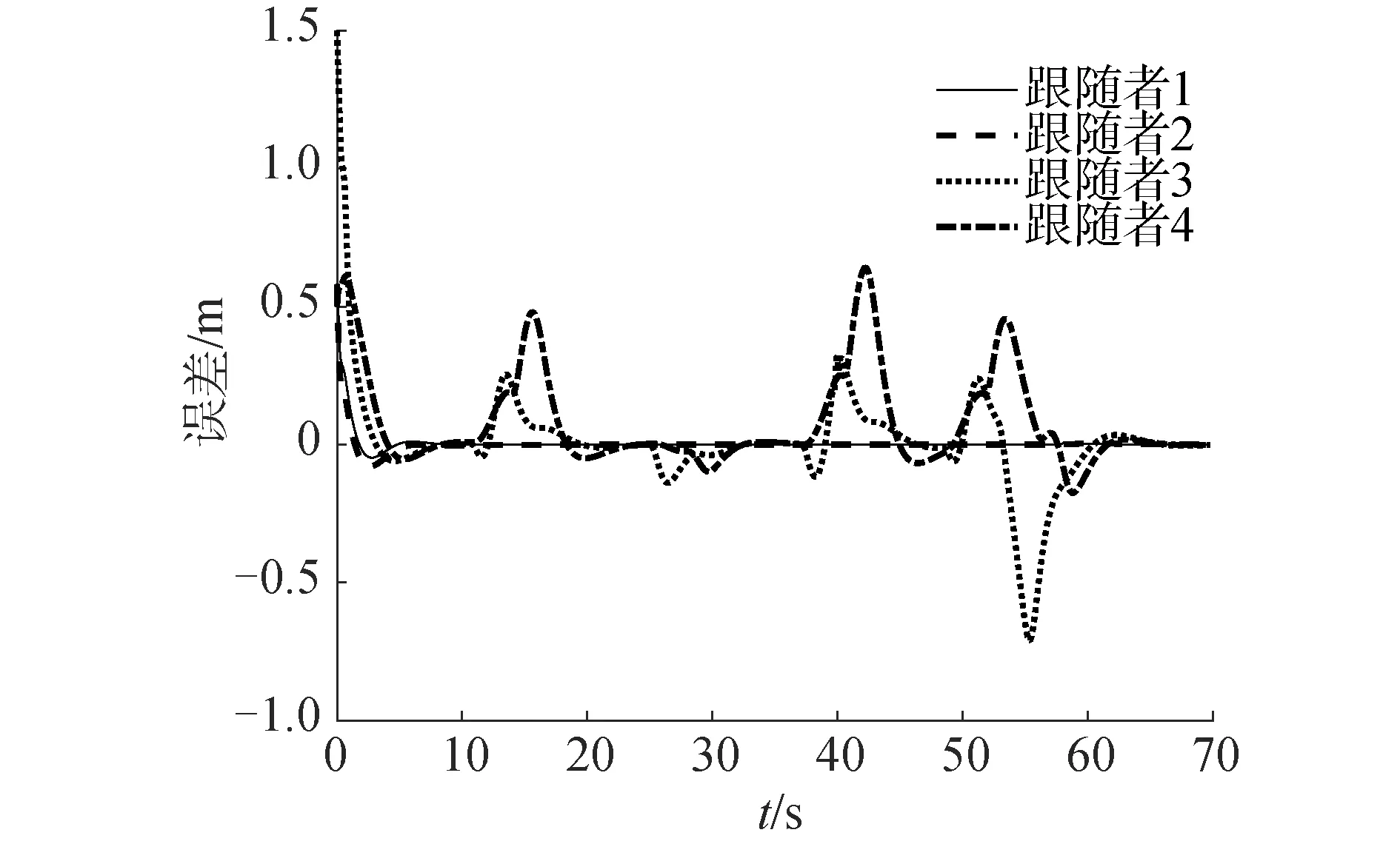
图9 ADRC算法理想误差曲线Fig.9 Ideal error curves of ADRC algorithms

由图6、7可知2种情况下虽然在一些路段上的路线不同,但编队和翼伞都可以按照一定的队列到达目标点。由图8、9可以看出ADRC方法地面网状回收平台形成编队以及遇到避障后重新编队的速度要比PID算法更快,在PID算法中还存在避障过程中领航者与跟随者之间位置误差震荡的情况,且其位置误差要大于同等状态下的ADRC算法。

3.2 实际情况的仿真结果

本文模拟伞降航天器匀速运动从而实现面面网状回收平台进行轨迹跟踪以及自主避障动作,需利用翼伞实际的轨迹数据检验程序的正确性和适用性,图10为翼伞实际的运动轨迹。

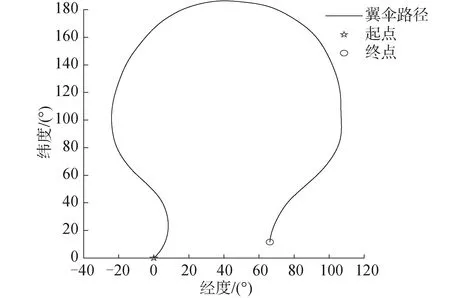
图10 翼伞实际轨迹Fig.10 Actual trajectory of parafoil

如图11、12分别为用PID和ADRC算法仿真出来的实际编队路径。地面网状回收平台按照预定的轨迹跟随着翼伞,在跟踪的过程中顺利的完成了自主避障过程,并且翼伞的位置一直处于4辆无人车中间,与理想情况相同,证实了程序的适用性。

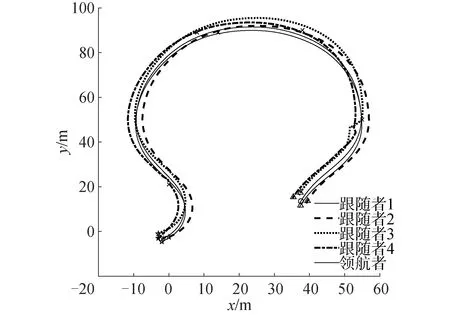
图11 PID算法实际编队路径Fig.11 Actual formation path of PID algorithms

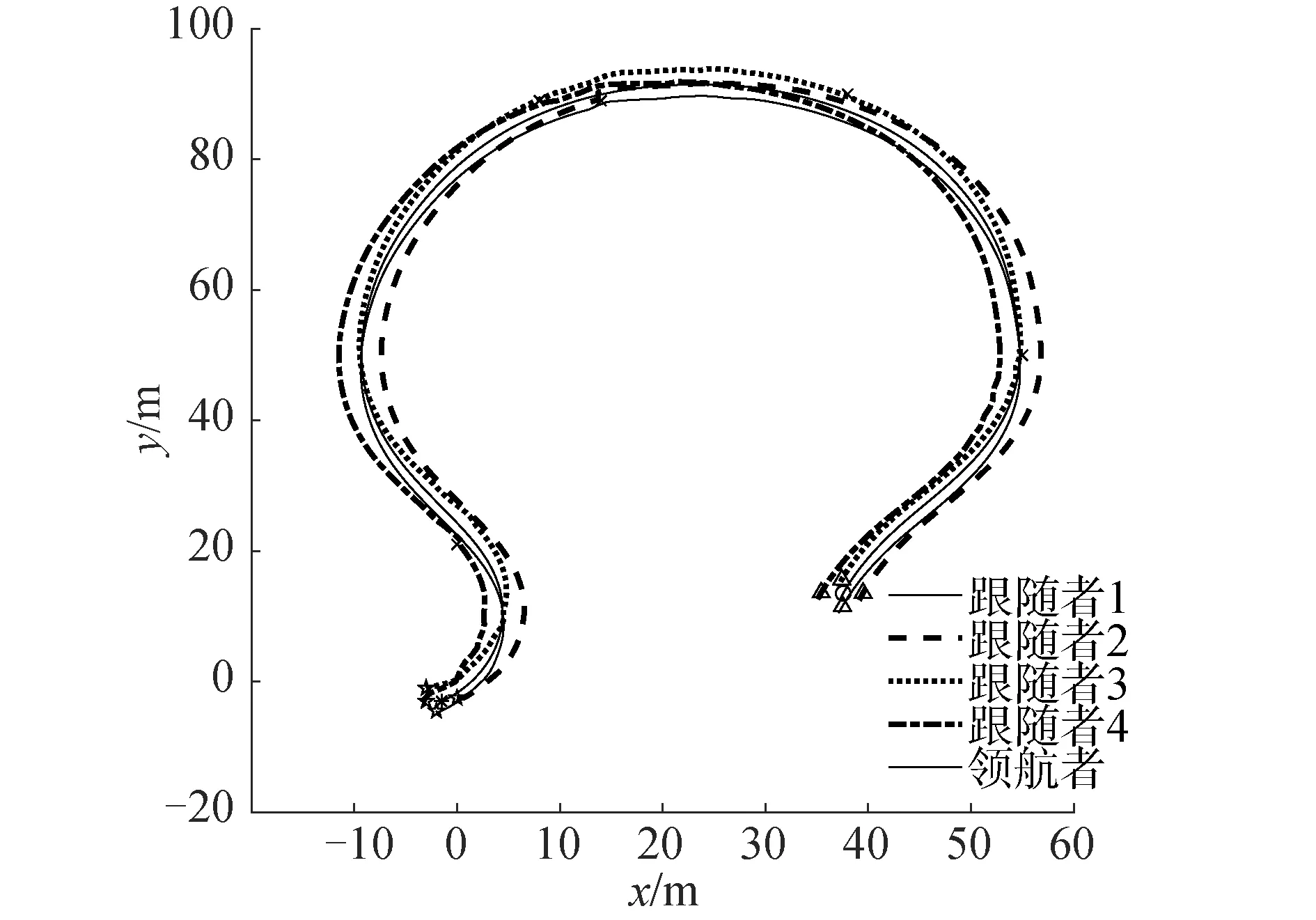
图12 ADRC算法实际编队Fig.12 Actual formation path of ADRC algorithms

如图13、14所示,ADRC情况下跟随者与领航者之间位置误差曲线要比PID情况下的曲线平稳的多,当遇到障碍物后PID算法实现的编队无法按照预定的要求形成稳定的编队,跟随者与领航者之间的误差很难达到0,而相对于ADRC算法来说,在遇到障碍物后无人车能够迅速的按照规定的要求形成稳定编队,并且其误差曲线也趋近于0。

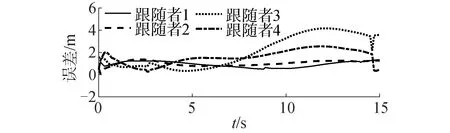
图13 PID算法实际误差曲线Fig.13 Actual error curves of PID algorithms

图14 ADRC算法实际误差曲线Fig.14 Actual error curves of ADRC algorithms

综上所述,与PID控制算法相比,ADRC控制算法具有较强的鲁棒性,能够有效改善由于无人车避障而导致编队整体稳定性遭到破坏的问题。

如表1所示,PID算法下领航者与跟随者之间的最大距离误差,平均误差以及误差的标准方差都要大于ADRC算法,综上所述,本文提出的伞降航天器无损回收系统中地面网状回收平台控制方法能够很好地解决航天器无损回收问题。

表1 领航者与跟随者距离误差Table 1 Distance error between pilot and follower

4 结论

1)本文通过利用由无人车形成的地面网状回收平台,成功实现了在陆地上对伞降航天器的无损回收。与原始的控制翼伞的飞行轨迹相比,此方法可以有效地解决翼伞无法精准降落从而需要很大的网回收伞降航天器的问题,并且能够减少航天器落地时的冲击力,达到了无损回收的效果。

2)与Space-X公司采用的海上无人船回收航天器的方法相比,本方法更加适应我国航天器降落地的地理情况,能够在陆地上对航天器进行回收。而利用单个无人船进行回收,不仅回收的范围受到回收网大小的限制,而且海面上的海浪大小、风力强度等不利因素对回收伞降航天器都有影响,再者单个无人船在海面上行驶的灵活性远远不如无人车在陆地上的灵活度。

3)本文使用ADRC控制算法来控制编队,与传统的PID算法相比,ADRC算法具有更好的抗扰动能力和更好的鲁棒性,能够更快速、稳定地达到预期效果,特别是在遇到扰动时。同时,本文还添加了无人车自主避障的程序,提高了编队对不同地形的适应能力,以及航天器无损回收过程中的容错率。

本文的实际应用价值在于为我国航天器的回收提供了一种更加有效的方案,具有广阔的市场前景和应用前景。未来,还可以进一步研究和优化无人车的自主避障能力、航天器的降落精度和网状回收平台的布置方案,以提高整个回收过程的效率和安全性。