基于ERA5海浪再分析数据的风浪涌浪分离方法
万勇, 沈培, 范陈清
(1.中国石油大学(华东) 海洋与空间信息学院,山东 青岛 266580; 2.自然资源部第一海洋研究所 海洋物理与遥感研究室,山东 青岛 266061)
近年来,随着中国经济的快速发展,我国海洋政策重心的不断调整,海洋工程建设及海洋能源的开发利用在持续进行中[1]。在海洋中作业主要受海浪影响,实际的海浪大部分是以不同成份的风浪与涌浪混合而成。其中,风浪是指由局地风直接引起的海浪;涌浪是指随着风速的陡然降低、风向的骤然改变传出风区的海浪。由于风浪和涌浪的成长、消衰、传播、破坏力机制都不同[2],根据复杂海浪状况中的海浪信息,深入研究风浪与涌浪的相关特性,详细描述当前海浪状态,有助于海洋科学的研究,避免海洋事故的发生,保证海上作业以及沿海民众生产生活的安全进行[3]。
迄今为止,风涌分离方法大致可分为波型方法、有向海浪谱方法和无向海浪谱方法[4]。其中,波型方法通过海浪的外表特征判别风浪与涌浪,由于该方法是通过海表面判断海浪状态,所以准确率较低;有向海浪谱是根据风与海洋表面相互作用产生能量生成海浪的原理,利用海浪方向谱和风速矢量信息来判断风浪与涌浪。因此,也被认为可以给出准确可靠的分离结果,通常被认定是风涌浪分离的标准方法。但需要考虑的信息量繁多,且在实践中不易获取,从而导致有向海浪谱风涌分离方法目前仍难以普及[5-12]。相比之下,无向风涌分离方法更适用于解决实际问题[13]。Earel[14]基于PM谱提出了分割频率和当地风速之间的经验性公式,根据分割频率分离风浪与涌浪。汪炳祥[15]利用波要素提出了一种在深水海浪与浅水海浪中识别涌浪的方法。Wang等[16]提出了风浪和涌浪的分割频率和波陡函数的峰值频率之间的关系式。Wang[17]基于PM谱修改了波陡函数的峰值频率跟分割频率之间的规律,提出了WH方法。Portilla[18]基于Sutherland提出的风浪成长所特有的超射现象,将海浪谱的各个峰值看作独立的波浪系统,实现风、涌浪的分离。李水清[19]对PM方法中分割频率的比例系数进行了调整,提高了风涌分离的准确性。Hwang[20]在波陡函数的方法基础上进行改进。Vincent[21]认为非线性相互作用机制与光谱中涌浪和海洋成分之间的能量转移有联系。
综上所述,无向海浪谱比有向海浪谱风涌分离方法更适用于实际应用[22-25]。无向海浪谱风涌分离中波龄方法是普遍应用的方法,但是由于波龄方法门限值的不确定性,存在准确性无法保证的缺陷。因此,有必要研究并建立风涌分离方法,解决目前无向海浪谱风涌分离精确度低的问题,为缺少风向信息的海域高效地分离海浪中风浪与涌浪、精确地描述海浪状态提供可靠的参考方法。
本文基于ERA5海浪再分析数据,利用有向海浪谱风涌分离方法得到了2018年印度洋海域风浪和涌浪作为本文建模数据集。分析了风浪与涌浪的平均波周期随风速的变化规律,利用最小二乘法定义了分离风浪与涌浪的新判别函数。基于2020年印度洋海域与南海海域的ERA5海浪再分析数据,对比分析波龄方法与TU方法的效果,验证了本文所提出的风涌分离方法的优势。
1 数据源
1.1 研究区域概述
本文的研究区域为中国南海海域(105°E~120°E,0°N~24°N)和印度洋海域(30°E~100°E,5°S~30°N),选择印度洋海域的数据进行方法的建模,选择印度洋和南海海域的数据验证平均波周期与网速,本文提出的风涌分离方法的可行性,探究各方法分离风、涌浪的效果是否受海域的影响[26-29]。如图1所示,波龄值的大小表示涌浪的强度,因此说明研究区域中不同经纬度的涌浪强度具有明显差异,即研究区域中包含了不同的海浪状态,选择的区域适合于开展本文的研究工作。
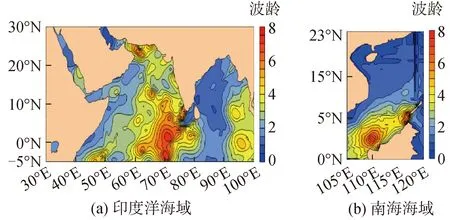
图1 2018年研究区域的涌浪强度分布Fig.1 Global distributions of swell index of the study area in 2018
1.2 ERA5数据
ERA5是ECMWF对全球气候的第五代大气再分析数据(the fifth generation ecmwf reanalyses,ERA5),几乎包含了描述风场和波浪场的所有参数,风场的数据包括海面10 m高度处的风速,波浪场的数据包括风浪、涌浪和混合浪的平均波周期等参数,能够提供比较精准的风浪、涌浪和混合浪的基础参数信息,为后续方法的建模与验证提供了数据源。考虑海浪场中波要素有着显着的季节性变化特征[29],本文首先提取了研究海域2018年一月、四月、七月以及十月的海浪数据,分析了不同月份以风浪为主和以涌浪为主的2组海浪数据中混合浪的平均波周期随风速变化的分布趋势,从而实现TU方法的建模。然后,选取2020年研究海域12个月份的ERA5海浪再分析数据,分析了不同月份波龄方法与TU方法判断风涌的正确率,并对TU方法的精度进行了验证。
2 TU方法的建模
本文根据能量因子的概念,处理了2018年印度洋海域ERA5海浪再分析数据,提取了以风浪为主和以涌浪为主2组海浪数据的平均波周期和风速作为本文研究的建模数据集。根据海浪是由高频风浪与低频涌浪组成原理,分析建模数据集中风浪数据与涌浪数据的分布规律。应用最小二乘法建立风涌分离方法。因本文根据平均波周期与风速的分布规律,建立了风涌分离方法。且一般情况下,用T表示平均波周期,U表示风速,本文将提出的风涌分离方法命名为TU方法。
2.1 数据集的建立
郭佩芳等[6]通过风浪谱和混合海浪谱的零阶矩,提出了混合浪能量成分因子的概念,并将其作为风、涌浪划分判据[7]。本文主要利用风浪、涌浪以及混合浪的有效波高信息和10 m风速,从海浪谱能量因子的角度出发,对研究海域的风、涌浪状况进行了初步的划分。其中零阶矩与特征参量有效波高H关系以及混合浪能量成分因子分别为:
M=H2/16
(1)

(2)
式中:M表示零阶矩;G表示能量因子;Mow、Mos和Mo分别为风浪、涌浪以及混合浪的零阶矩。
当G<2时,判断此时是以风浪为主。当G≥2时,判断此时的海浪是以涌浪为主。因此,本文从能量的角度,为建模数据集和验证数据集提供了准确值。
2.2 TU方法的建立
本文利用基于能量因子的风涌分离方法,将2018年印度洋海域的ERA5海浪再分析数据分成以风浪为主和以涌浪为主2组海浪数据作为建模数据集。因为风浪与涌浪是海洋表面2种主要的重力波,风浪是在风的作用下产生的,受风的影响比较大;而涌浪是在海面上遗留下来的浪,无法从原来的风场中获取能量,因此海浪状态与风信息有密不可分的联系[29]。考虑风速是较容易得到的信息,所以为达到利用较少的海浪特征参数实现风、涌浪分离的目的,选择从风速和平均波周期2个角度,对风浪和涌浪的分布关系进行分析。通过提取印度洋海域2018年一月份、四月份、七月份和十月份的风速和平均波周期,分析了风、涌浪数据的分布规律,如图2所示。
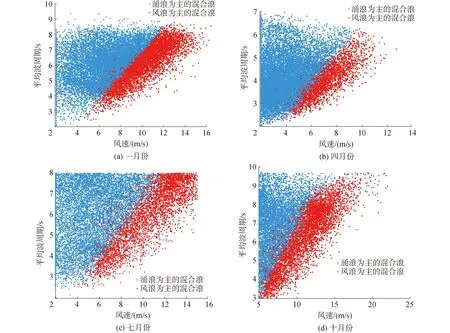
图2 2018年印度洋海域不同海浪状态下风速与平均波周期的关系Fig.2 Graphs of wind speed and mean wave period under different wave states in the Indian Ocean in 2018
可见当风速小于4 m/s时,大多数海浪数据以涌浪为主,随着风速的上升,以风浪为主的海浪数据逐渐变多,以涌浪为主的数据逐渐减少,风浪和涌浪数据的平均波周期具有明显的分布规律,海面风速和平均波周期在海平面上升到充分发展阶段呈单调关系。因此,可以通过拟合直线区分风浪和涌浪。
根据以上分析,为拟合得出海浪状态成熟度分界线,达到风、涌浪数据分离的目的,需先从建模数据集中提取风、涌浪2组数据的边界数据,得到充分发展阶段的海面风速和平均波周期数据,定义拟合函数类型为y=ax2+bx+c,其中自变量为U10,因变量为T,通过最小二乘法拟合确定TU方法中的待定系数,得到系数分别为-0.02、1.115和-2,即获得TU风涌分离公式:
(3)
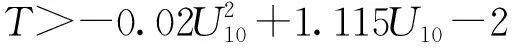

图3 2018年印度洋海域TU方法划分风、涌浪效果Fig.3 TU method divides wind sea and swell in the Indian Ocean in 2018
3 方法的验证与比较
本文从判断风、涌浪的正确率和稳定性2个角度对TU方法与波龄法的分离效果进行了对比与分析,通过不同海域、不同月份的对比。
3.1 波龄方法
波龄是风浪成长率的指标,当波龄达到门限值时,标志着风浪达到了充分发展的海浪状态,即此时的海浪从以风浪为主的海浪转变为以涌浪为主的海浪。波龄门限值β为:
(4)
一般波龄的门限设置在1.4~1.7[32]。为保证波龄方法判定涌浪的效果,将波龄设置为门限范围内的最低值,即β>1.4的情况下,认为此时海面的海浪以涌浪为主,否则以风浪为主。波龄方法使用平均波周期和风速2个参数识别风、涌浪状况,是目前应用较为广泛的无向海浪谱风涌分离方法。根据得到的建模数据集,可见风浪与涌浪数据有明显分布规律,但波龄方法划分风、涌浪数据时存在较多风浪误判成涌浪的现象,如图4所示。且波龄目前没有固定的门限值,导致识别风浪与涌浪的效果具有不确定性。针对以上问题,接下来将通过比较TU方法和波龄方法识别风浪与涌浪数据的正确率和稳定性,说明拟合提出TU方法的优越性。
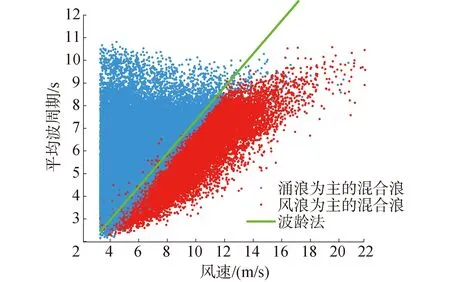
图4 2018年印度洋海域中波龄方法划分风、涌浪效果图Fig.4 Wave age method divides wind sea and swell in the Indian Ocean in 2018
3.2 TU方法的验证
根据基于能量因子的风涌分离方法介绍,利用ERA5海浪再分析数据,对2020年南海海域与印度洋海域进行风、涌浪分离,得到了风、涌浪的分离结果作为验证数据集。然后分别计算TU方法和波龄方法分离风、涌浪的正确率和方差为:
P=x1/x2
(5)
(6)
式中:P表示正确率;x1表示正确判别的涌浪样本数;x2表示验证数据集中涌浪样本数;D(p)表示涌浪方差;M表示正确率的平均数;n为12,即12个月。
根据计算得出正确率和方差,得到折线图,如图5所示,y1和y2分别表示波龄方法和TU方法判断风浪的正确率,y3和y4分别表示波龄方法和TU方法判断涌浪的正确率。
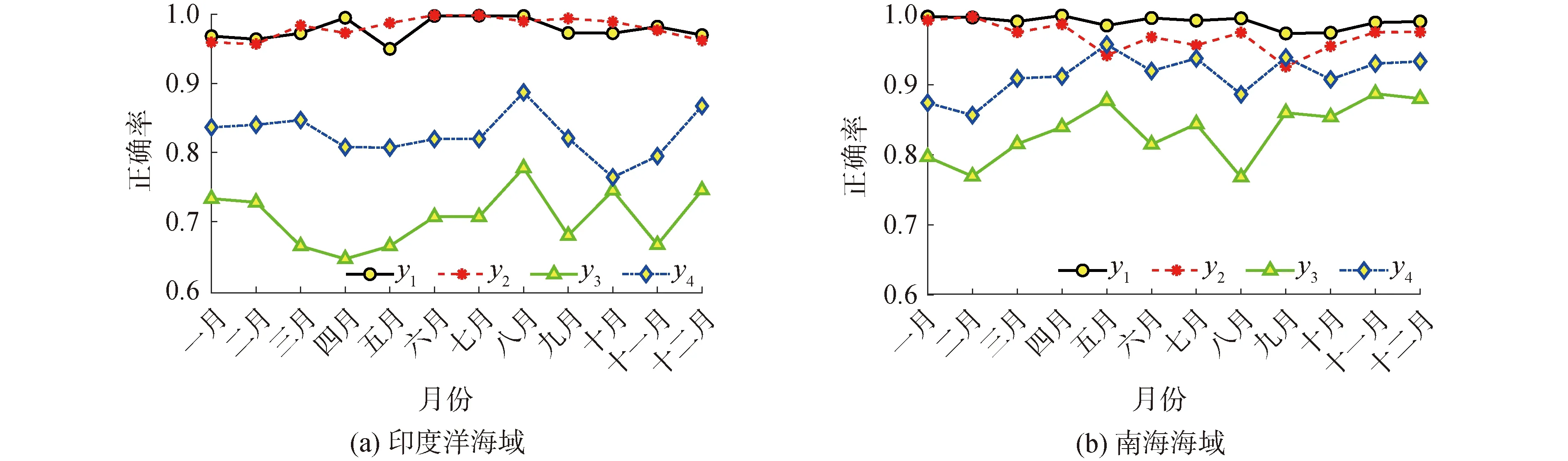
图5 2020年研究海域中波龄方法与TU方法判定风、涌浪数据的正确率Fig.5 The accuracy of wave age method and TU method divides wind and swell data in the sea area in 2020
可以看出尽管TU方法和波龄方法判断风浪的正确率相近,但是TU方法判断涌浪的正确率80%~90%左右,明显高于波龄方法。且印度洋海域y1、y2、y3和y4的方差分别为1.50、1.44、3.9和3.1,南海海域y1、y2、y3和y4的方差分别为8.9、5.4、12.2和5.48,方差越小说明该方法在各种情况下的精度表现更稳定,方法的适用性更好,因为TU方法的方差远小于波龄方法,所以适用性比波龄方法更好。根据以上对比分析,综合考虑2种方法识别涌浪的准确率和方差,可得出结论:TU方法判断涌浪的准确性和稳定性皆优于波龄方法,在分离风、涌浪方面可以取得更好的效果。
4 结论
1)本文提出的TU方法判断涌浪的准确性和稳定性皆优于波龄方法,可作为风涌分离的判据。
2)本文提出的风涌分离TU方法,在风浪和涌浪成分分离方面有一定的局限性,即只能判断海浪是风浪主导还是涌浪主导。
3)与先前的研究工作不同的是,本文利用了平均波周期与风速实现风流涌浪的分离,先前的波要素风涌分离方法以有效波高和风速分离风浪与涌浪较多。
4)本文只需风速与平均波周期2个海浪参数,即可实现风、涌浪的分离,为一些需要判断涌浪的研究提供了便捷的方法,如海浪建模,卫星算法的验证,海岸工程和船舶航线等,对高度计等无风向信息的海浪遥感探测复杂海域也具有重要的意义。

