牛腿式接缝分段预制拼装盖梁的受力性能

李长春, 卓卫东, 孙作轩, 肖泽荣, 陈冠华, 黄新艺

(1.福州大学 土木工程学院,福建 福州 350108; 2.福州市规划设计研究院集团有限公司,福建 福州 350108)

长期以来,我国桥梁建造采用以现场浇筑混凝土为主的施工方式,存在施工周期长、质量不稳定、环境污染大等弊端,特别是在城市环境里,较长的工期阻断交通,造成了极大的社会损耗成本,同时施工噪音及扬尘严重污染了城市环境。为了解决传统现浇施工方式存在的弊端,预制拼装技术越来越受到青睐[1-3]。然而,在装配式城市桥梁中,混凝土盖梁的预制装配化问题却一直难以得到解决,主因是整体预制混凝土盖梁往往呈现长悬臂、大体积、自重大等特点,严重受限于城市道路通行能力以及城市桥梁建设场地面积,难以运输与吊装。分段预制拼装预应力混凝土盖梁技术是解决整体现浇盖梁运输和吊装难题的一种有效方案,并已在众多工程项目中得到成功应用。从国内外的工程实践来看,分段预制拼装预应力混凝土(precast assembled concrete,PC)盖梁主要以横向分段为主,现场拼装只对接缝处进行处理,无需立模浇筑[4]。目前,对分段预制拼装PC盖梁接缝的认识主要来自于对分段预制拼装PC梁的接缝研究。文献[5-9]均通过一系列试验,研究了接缝类型对分段预制拼装混凝土梁受力性能的影响。采用胶接缝的分段预制PC梁的受力性能优于采用干接缝的分段预制PC梁,而且接近于整体现浇PC梁。利用胶接缝的分段预制拼装大悬臂PC盖梁在弹性阶段的力学性能与整体现浇PC盖梁基本相同,但接缝是分段预制拼装盖梁薄弱环节,导致极限荷载明显低于后者,且破坏时裂缝疏而宽[10-11]。因此,对胶接缝的准确模拟是有限元模型的关键点。采用不同模拟方法模拟胶接缝,均无法准确模拟胶接缝处混凝土开裂及胶体与混凝土界面因粘结强度不足发生张拉开裂现象[12-14]。对分块预制拼装PC盖梁,实践中常用的接缝构造主要有大键齿、小键齿、钢键式和牛腿式构造等[4],其中,牛腿式接缝构造具有较佳的施工性能。与实践应用相比,国内外对分段预制拼装PC盖梁的理论研究均已严重滞后。

为深入研究牛腿式接缝分段预制拼装PC盖梁的受力性能,本文在模型试验基础上,采用ABAQUS软件建立其非线性有限元模型,探讨胶接缝的合理模拟技术,并通过参数分析,探索接缝位置、预应力水平、预应力筋数量、胶体粘结失效面积和截面尺寸等因素对其受力性能的影响规律。

1 盖梁模型静力试验

1.1 试验概况

本文以福州市新店外环路西段道路工程主线高架桥采用的预制拼装PC盖梁为原型,原型结构采用实心多边形截面,横桥向宽25.2 m,纵桥向长2.2 m,中间段梁高1.9 m,悬臂长度达6.8 m。模型采用1∶5几何缩尺比例,长5 040 mm。根据截面面积及惯性矩不变的原则,将原型盖梁截面按相似关系简化为500 mm×390 mm的等效实心矩形截面,悬臂段也由变截面简化为等截面。原型盖梁与墩柱的线刚度之比为1.21,为正确模拟这一关系,调整墩柱高度为1 000 mm,墩柱截面尺寸为400 mm×320 mm。

本文分别按整体预制和分段预制方案共设计了2个大悬臂PC盖梁模型。其中,ZT0模型为整体预制盖梁模型;NT1模型为牛腿式接缝分段预制拼装盖梁模型,NT1模型采用现阶段主流的“横向分三段方案”[4],根据工程经验,接缝设置在距立柱外侧0.225 m 处。2个模型均采用原型材料制作,盖梁混凝土强度为C50,纵筋和箍筋均采用HRB400级钢筋;牛腿式构造内配置抗剪钢筋。图1为模型的构造尺寸及配筋示意图。

试验模型的盖梁部分为后张有粘结预应力构件,共布置3束通长的预应力钢束。其中N1束1束,由3根1×7-15.24-1860-GB/T 5224-2014的预应力钢绞线组成,位于截面的竖向对称轴上;N2束2束,各由2根与N1束同型号的预应力钢绞线组成,沿截面左右对称布置;所有预应力钢绞线均为曲线布置,无平弯,预应力筋布置如图2所示。

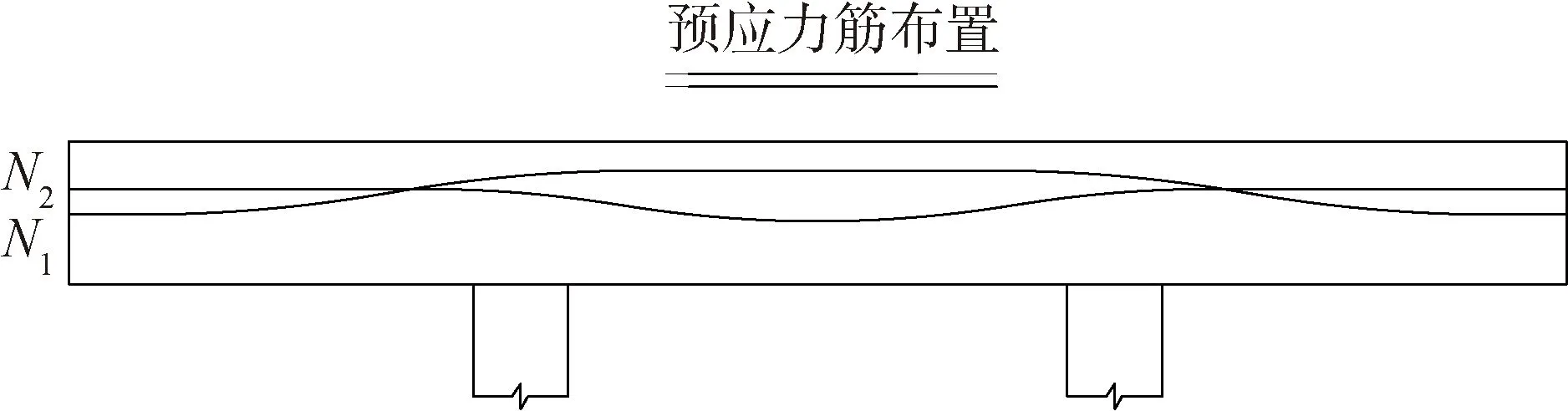
图2 预应力筋布置示意Fig.2 Layout of prestressed reinforcement

在原型结构中,上部结构恒、活载通过5个支座传递给盖梁。本文对模型加载方案进行简化,仅在两侧悬臂端部单点加载,该方案为一种最不利的加载方案,可充分探究NT1模型整体及接缝处的受力性能。图3为试验加载装置,包括2个2 000 kN千斤顶和1个5 000 kN的反力架系统。采用单调分级加载制度逐级施加静力荷载,直至盖梁模型破坏为止。

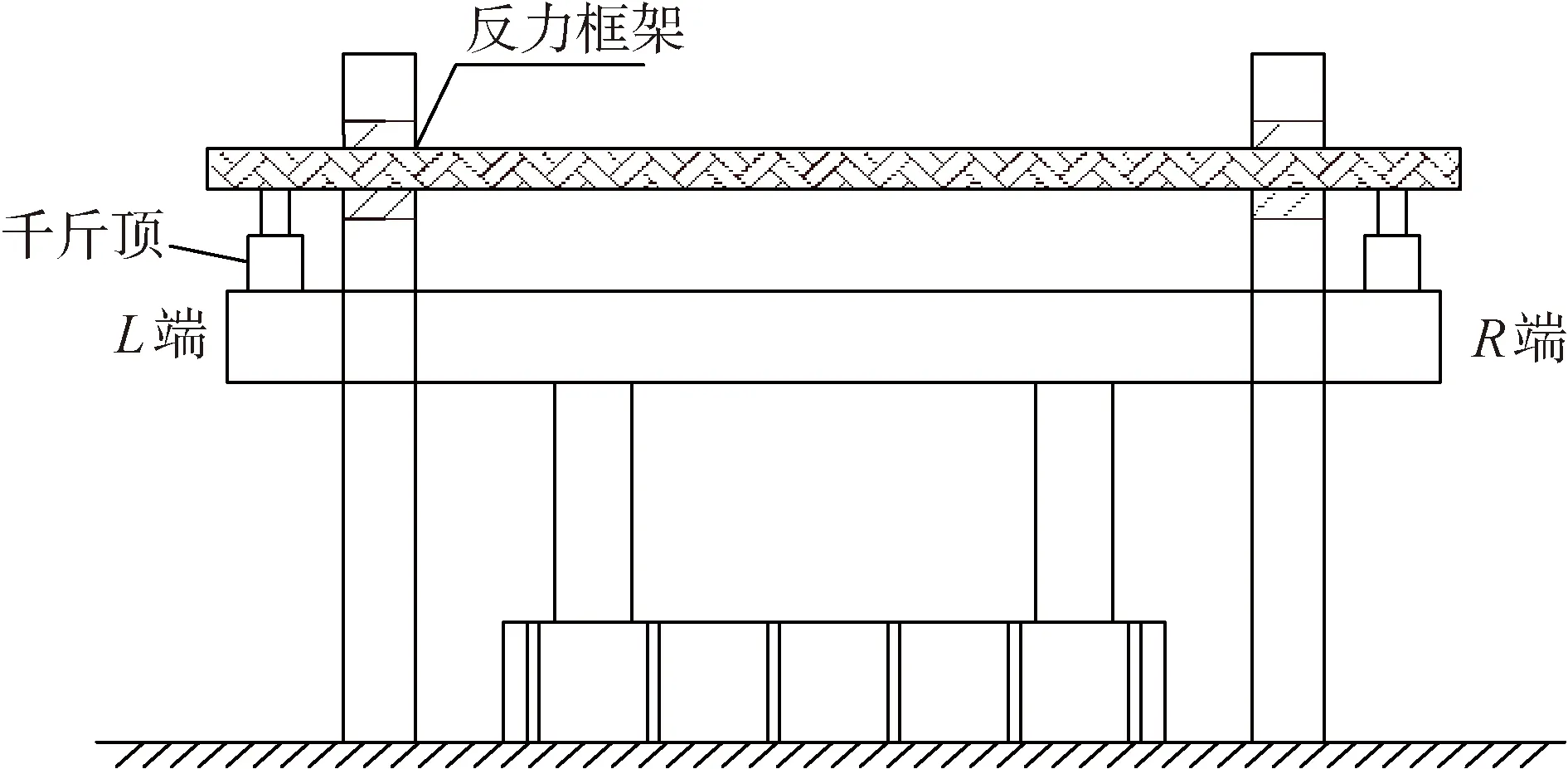
图3 试验加载装置示意Fig.3 Schematic diagram of test setup

试验量测内容包括试验荷载、梁体混凝土应变、挠度和裂缝等。利用标定后的50 t压力传感器测量试验荷载;沿梁纵向共布置11个竖向位移传感器,以测量梁体挠度;选取全梁多个典型截面测试混凝土应变,包括跨中截面及接缝截面,并沿盖梁长度方向在顶、底板布置一定数量的应变片,观测全梁混凝土应变变化情况。试验中,同步观察并记录各级荷载下裂缝发展情况。

1.2 试验结果

图4为2个盖梁模型实测的加载点荷载-挠度曲线,ZT0和NT1模型的荷载-挠度曲线均呈现出较为明显的弹性阶段、裂缝发展阶段和破坏阶段的3阶段特点:1)当荷载较小、梁体未开裂时,各模型均处于弹性阶段,挠度随荷载的增大近似呈比例增大,且初始刚度相同;2)超过开裂荷载后,各模型均进入裂缝发展阶段,曲线斜率随荷载增大不断减小,非线性特征明显。在裂缝发展的大部分阶段,2个模型的切线刚度都基本相同,在后期NT1模型的切线刚度才明显低于ZT0模型;3)进入破坏阶段后,曲线斜率接近于零,梁体挠度增长迅速,各模型最终因梁体受压区混凝土被压碎而破坏。与ZT0模型相比,NT1模型的极限承载力和极限变形能力分别减小了16%和25%,下降幅度明显。

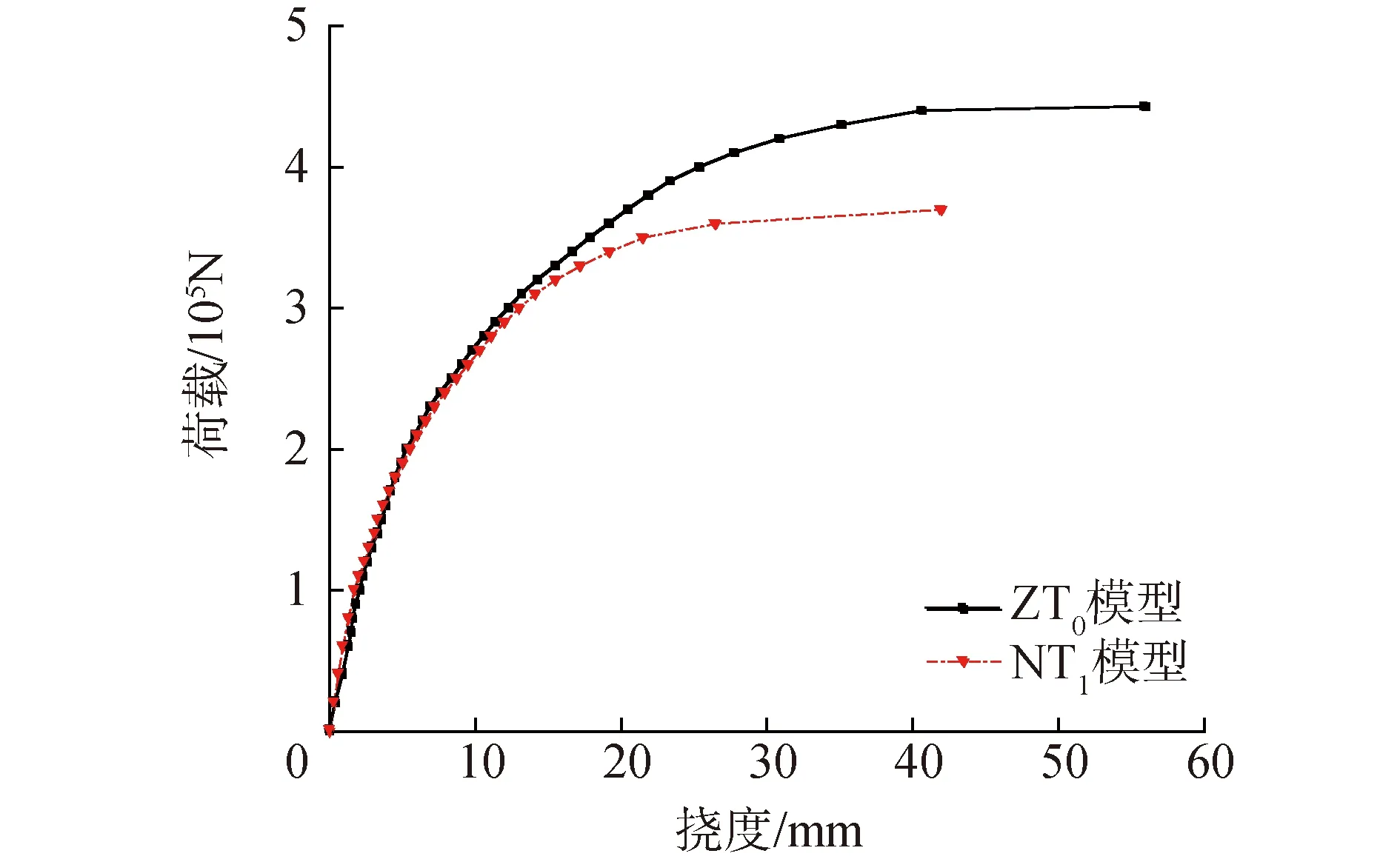
图4 试验模型荷载-挠度曲线比较Fig.4 Comparison of load-deflection curves of test models

图5所示为2个盖梁模型实测的最大裂缝宽度随荷载的变化曲线,各盖梁模型的裂缝宽度发展可概括为开裂初期-中期-后期3个发展阶段:在开裂初期,裂缝宽度发展较慢;在裂缝发展中期,其宽度发展明显加快;在裂缝后期,其裂缝宽度急剧增长。

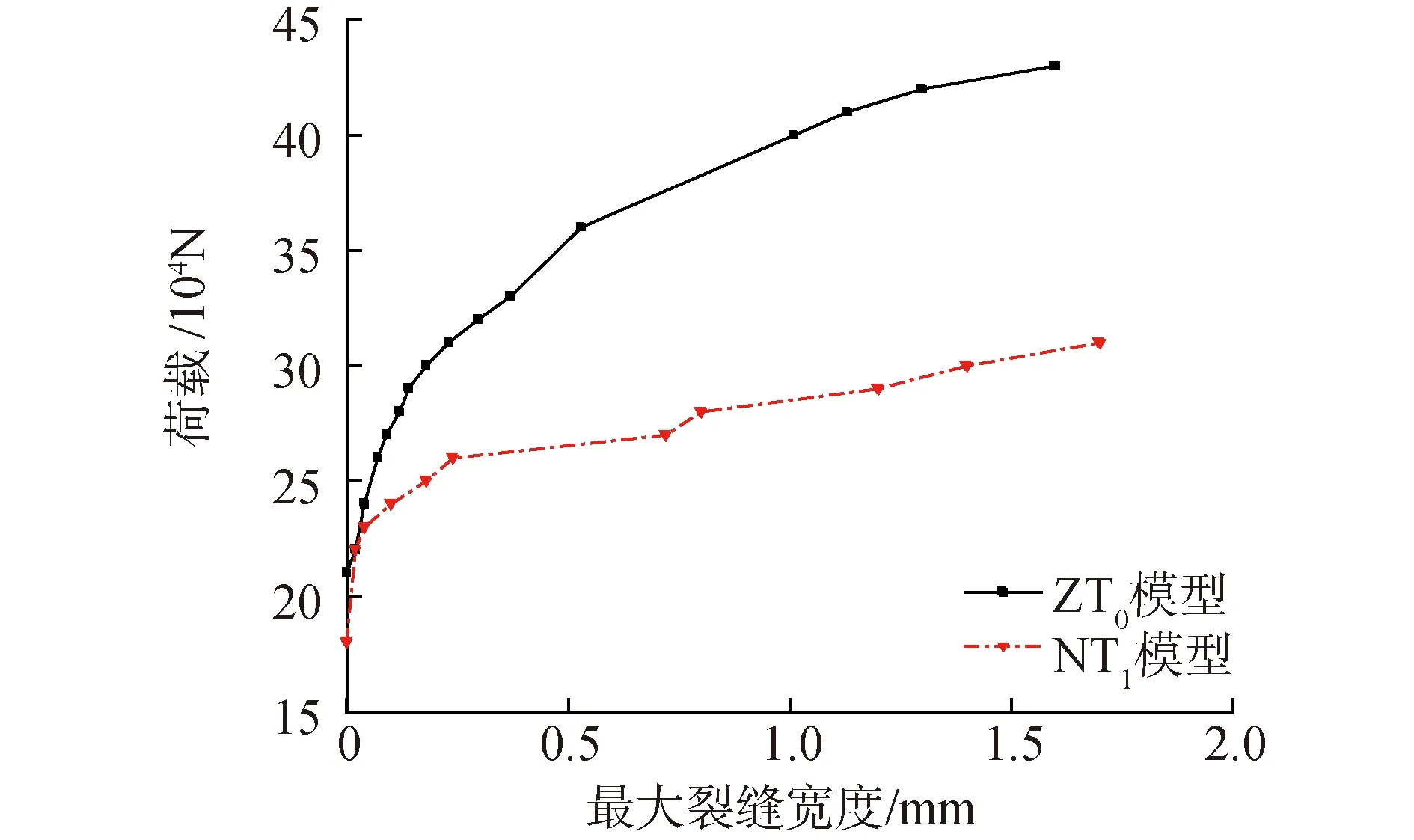
图5 试验模型荷载-最大裂缝宽度曲线比较Fig.5 Comparison of load-maximum crack width curves of test models

NT1模型与ZT0模型相比,两者开裂荷载相同,但前者裂缝宽度发展更快,且破坏时最大裂缝宽度已远远超出裂缝观测仪的2 mm量程范围,而后者破坏时最大裂缝宽度仅为1.6 mm。造成此现象的原因,源于NT1模型牛腿接缝两侧纵向普通钢筋不连续,使接缝界面成为整个盖梁结构的薄弱环节,在破坏阶段牛腿接缝附近的主裂缝宽度开展较大。

图6显示2个盖梁模型在达到极限承载力时的裂缝分布和破坏形态,可以看出,ZT0和NT1模型的裂缝分布形态基本相同,破坏时梁体裂缝分布稀疏,且裂缝宽度较大;从破坏形态看,2个模型都是在弯矩最大截面(悬臂根部)梁体底部混凝土被压碎而破坏,NT1模型牛腿接缝构造未发生剪切破坏。与ZT0模型相比,NT1模型的裂缝主要分布在胶接缝与悬臂根部之间,胶接缝到自由端之间没有出现裂缝;此外,破坏时接缝界面内侧的主裂缝宽度较大,受拉区混凝土完全分离,表明牛腿接缝界面是其薄弱环节。

图6 试验模型裂缝分布与破坏形态Fig.6 Crack distribution and failure mode of each model

2 有限元模型及验证

2.1 试验模型有限元模拟

采用ABAQUS软件,分别建立ZT0和NT1模型的精细化有限元模型。鉴于模型尺寸较大,为提高计算效率,根据结构的对称性,仅建立1/2结构有限元模型。图7为本文建立的NT1模型的有限元模型,其中,混凝土单元网格尺寸总体控制为50 mm,高度方向取为39 mm;对胶接缝附近区域进行局部网格加密,控制网格任意两边长之比小于3,采用结构化网格划分。钢筋及预应力筋网格长度取为100 mm,为混凝土网格的1～4倍。

图7 NT1模型的有限元模型Fig.7 Finite element model of NT1 model

建模中,普通混凝土单元采用8节点六面体线性减缩积分单元(C3D8R),本构模型选为塑性损伤模型,部分参数取值如表1所列。预应力筋及普通钢筋采用2节点桁架单元(T3D2),本构模型分别采用理想弹塑性模型和二折线模型;采用嵌入约束将预应力筋、普通钢筋骨架与混凝土实体进行连接。

表1 塑性损伤模型部分参数取值Table 1 Some parameter values of plastic damage model

对NT1模型,接缝构造的准确模拟是建立正确有限元模型的关键,通常采用实体单元、绑定约束、弹簧单元和接触单元等4种模拟方法。其中,绑定单元无法有效模拟胶接缝界面开裂现象,而实体单元存在局部网格划分密度过大的问题。此外,NT1模型胶接缝厚度仅为2～3 mm,相对于模型长度可忽略不计,也不宜采用实体单元模拟。因此,本文分别采用粘性接触单元和弹簧单元模拟胶接缝界面。通过模型试验发现,胶接缝界面会存在一定的环氧树脂粘结剂脱空现象,故采用粘性接触单元模拟胶接缝时,将损失起始应力取为2.5 MPa(对粘结强度最大值3 MPa进行折减);界面刚度K取值目前还缺乏理论依据和经验,本文经试算,将接触界面刚度K取值为2×104MPa/mm。

预应力荷载施加采用降温法[15],在初始分析步中设置初始温度为0 ℃,随后在下一个分析步中设置温度-477 ℃;为了便于计算收敛,加载方式采用位移加载[16]。边界条件取为柱底固结。

2.2 有限元模型验证

为验证有限元模型的正确性,首先将ZT0模型的计算结果与试验结果进行对比。图8给出有限元模型计算得到的荷载-挠度曲线与试验实测曲线对比,可以发现,两者曲线发展规律总体一致,极限荷载也几乎相同,均在440 kN左右。与试验实测曲线相比,有限元模型计算得到的曲线斜率总体较大,分析两者差异的原因,主要源于有限元模型假定柱底固结,而试验模型柱底无法实现理想固结边界条件。此外,有限元模型中忽略钢筋与混凝土间的粘结滑移,也使其刚度偏大。

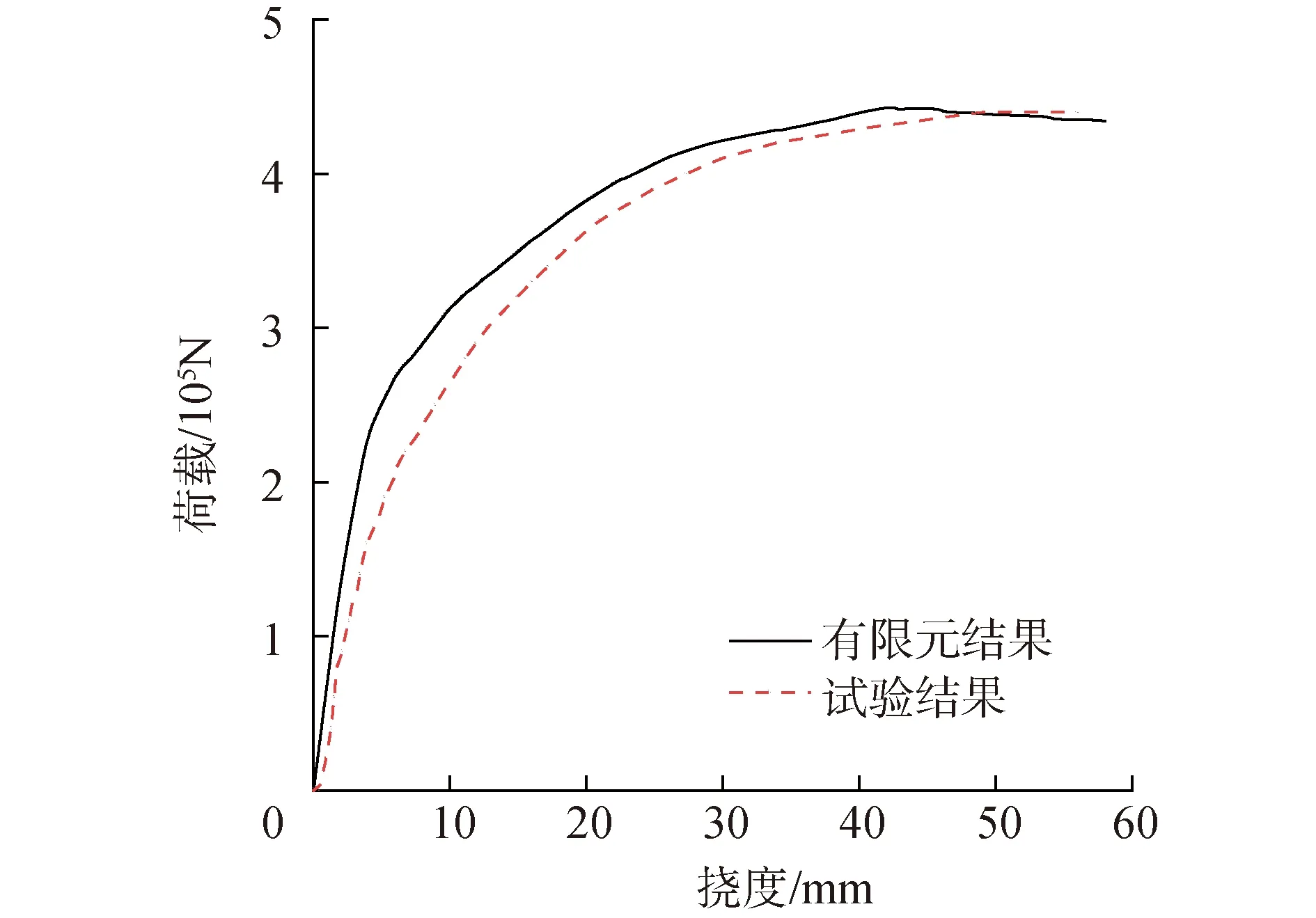
图8 ZT0模型有限元与试验荷载-挠度曲线对比Fig.8 Comparison of load-deflection curves of ZT0 model between FE and test results

图9显示有限元模型计算得到的ZT0模型破坏时的裂缝分布和破坏形态。与图6对比可以看出,两者裂缝分布基本吻合,且破坏形态均表现为悬臂根部梁体底部混凝土被压碎。

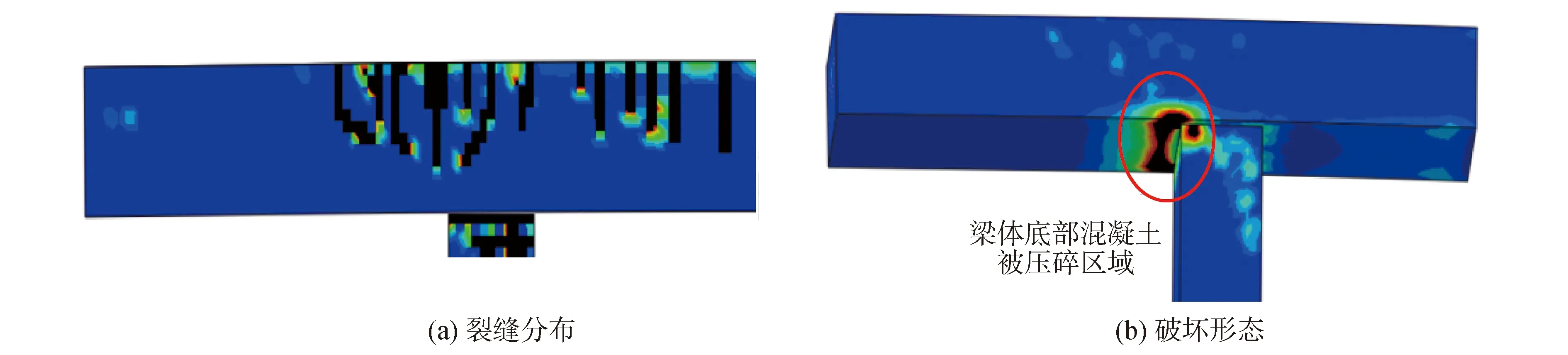
图9 ZT0模型有限元与试验破坏现象对比Fig.9 Comparison of failure phenomena of ZT0 model between FE and test results

图10为NT1模型由有限元模型计算得到的荷载-挠度曲线及荷载-最大裂缝宽度曲线与试验实测曲线对比,可以看出,采用粘性接触单元模拟胶接缝的有限元模型计算得到的结果与试验结果吻合较好,而采用弹簧单元模拟胶接缝的有限元模型得到的结果与试验结果相差较大,特别是最大裂缝宽度计算结果差异明显。分析有限元计算结果与试验结果存在差异的原因,主要在于弹簧单元刚度取值由环氧树脂粘结剂的弹性模量确定,而试验现象观察表明,裂缝是从接缝界面内侧混凝土开始发展的,胶层并未破坏;粘性接触单元的界面刚度综合考虑了胶接缝及临近混凝土的材料特性取值,能够更合理地模拟裂缝从临近接缝混凝土产生并发展的现象。

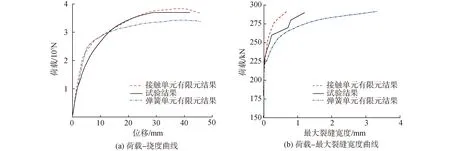
图10 NT1模型有限元与试验结果对比Fig.10 Comparison between FE and test results of NT1 model

3 有限元的参数分析

由于本文仅开展了1个牛腿式接缝分段预制拼装PC盖梁模型的静载试验,为弥补试验次数的不足,通过有限元模型进行参数拓展分析。对盖梁模型的有限元模拟结果表明,有限元模型可较好地模拟PC盖梁在静载作用下的受力全过程。其中,对牛腿式接缝分段预制拼装PC盖梁,采用粘性接触单元模拟牛腿接缝,亦可得到满意的结果。

采用经验证的建模技术,本文对牛腿式接缝分段预制拼装PC盖梁开展有限元模型参数分析,探索接缝位置、预应力因素、接缝粘结失效面积、盖梁截面尺寸等对结构受力性能的影响规律。

3.1 接缝位置影响分析

接缝位置是牛腿式接缝分段预制拼装PC盖梁设计的关键参数之一,通常接缝位置设置需综合考虑施工便捷性、有效减轻最大起吊重量且避免冲突和延缓胶接缝区域开裂3个原则。考虑到接缝位于两柱之间难以进行拼装作业,故本文仅考虑接缝设于悬臂段的情况,共设置3种分析工况,如图11所示,工况1、工况2、工况3分别距离悬臂根部外侧625、425、225 mm,其余设计参数与NT1模型相同。经有限元模型计算,工况1、工况2和工况3分别能减轻最大吊重28%、37%和44%,即悬臂段的接缝位置越靠近悬臂根部,越能有效减轻盖梁的最大吊重。

图11 3种不同接缝位置工况Fig.11 Three different joint positions working conditions

图12给出不同分析工况下盖梁加载点位置的荷载-挠度曲线,可以发现,接缝位置对弹性阶段和裂缝发展阶段曲线基本没有影响,对破坏阶段曲线有一定影响;越靠近悬臂根部,盖梁的极限承载力越低,与工况1相比,工况2、工况3的极限承载力分别下降了4.0%和7.4%。可见,接缝位置设置基本不影响开裂荷载,然而减轻盖梁的最大吊重与极限承载力有所冲突,设计时应综合考虑机械设备起吊能力和结构受力性能,设置符合需求的接缝位置。

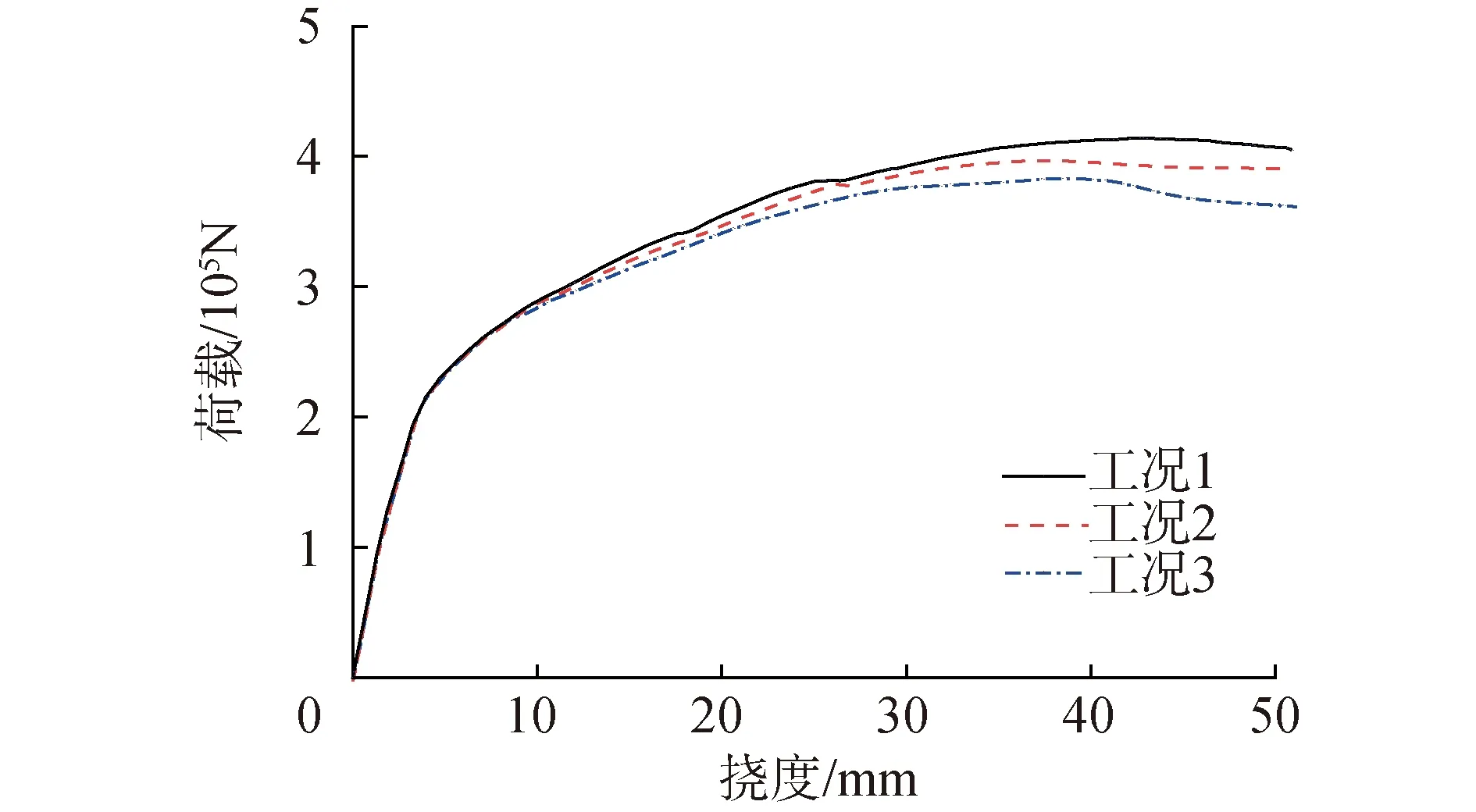
图12 不同工况荷载-挠度曲线Fig.12 Comparison of load-deflection curves among three different cases

3.2 预应力因素影响分析

原型盖梁模型在预应力张拉完成后悬臂段处于上缘受压、下缘受拉的预压状态,接缝界面沿高度方向弯曲正应力分布不均匀。为研究不同预应力水平的影响,以有效预应力为分析参数,将其分别设为0.75σcon、0.70σcon、0.65σcon和0.60σcon4个水平进行分析,其余设计参数与NT1模型相同。

图13为不同有效预应力水平下盖梁加载点位置的荷载-挠度曲线,可以发现,正常取值范围内,有效预应力大小对牛腿式接缝分段预制拼装PC盖梁的弹性段曲线基本没有影响,随着有效预应力的增大,其开裂荷载和极限承载力均相应增大,而与极限荷载对应的位移(下文简称为峰值位移)则相应减小:与有效预应力为0.60σcon的分析工况相比,当有效预应力达0.75σcon时,开裂荷载和极限承载力分别增大了16.9%和3.5%,而峰值位移减少24.4%。分析原因,是因为有效预应力不能改变牛腿式接缝分段预制拼装PC盖梁的初始刚度,但提高有效预应力可延长其弹性段范围,增大接缝附近混凝土开裂面的摩阻力和预应力筋的销栓力,并减小主裂缝宽度,故在一定程度上提高了其极限承载力和破坏阶段的刚度。

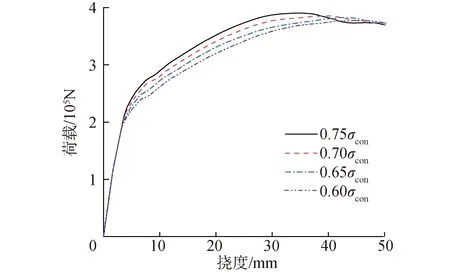
图13 不同有效预应力水平下荷载-挠度曲线比较Fig.13 Comparison of load-deflection curves among different effective prestress levels

为进一步分析预应力筋数量的影响,设置5种分析工况,与工况1～5对应的预应力筋根数分别为7根、10根、13根、14根和15根,各预应力筋的有效应力均取为标准强度的75%,其余设计参数与NT1模型相同。图14为不同预应力筋数量下盖梁加载点位置的荷载-挠度曲线,可以发现,预应力筋数量对牛腿式接缝分段预制拼装PC盖梁的受力性能有较大影响,其初始刚度、开裂荷载和极限承载力均随预应力筋数量的增多而相应增大,而峰值位移则相应减小。与工况1相比,工况2～5的极限承载力分别提高了17.1%、29.5%、36.1%和39.2%,均超出整体现浇PC盖梁模型的极限承载力,峰值位移分别减小了29.7%、34.8%、39.8%和46.6%,说明增加预应力筋的数量可明显提高牛腿式接缝分段预制拼装PC盖梁的极限承载力,并减小其峰值位移。

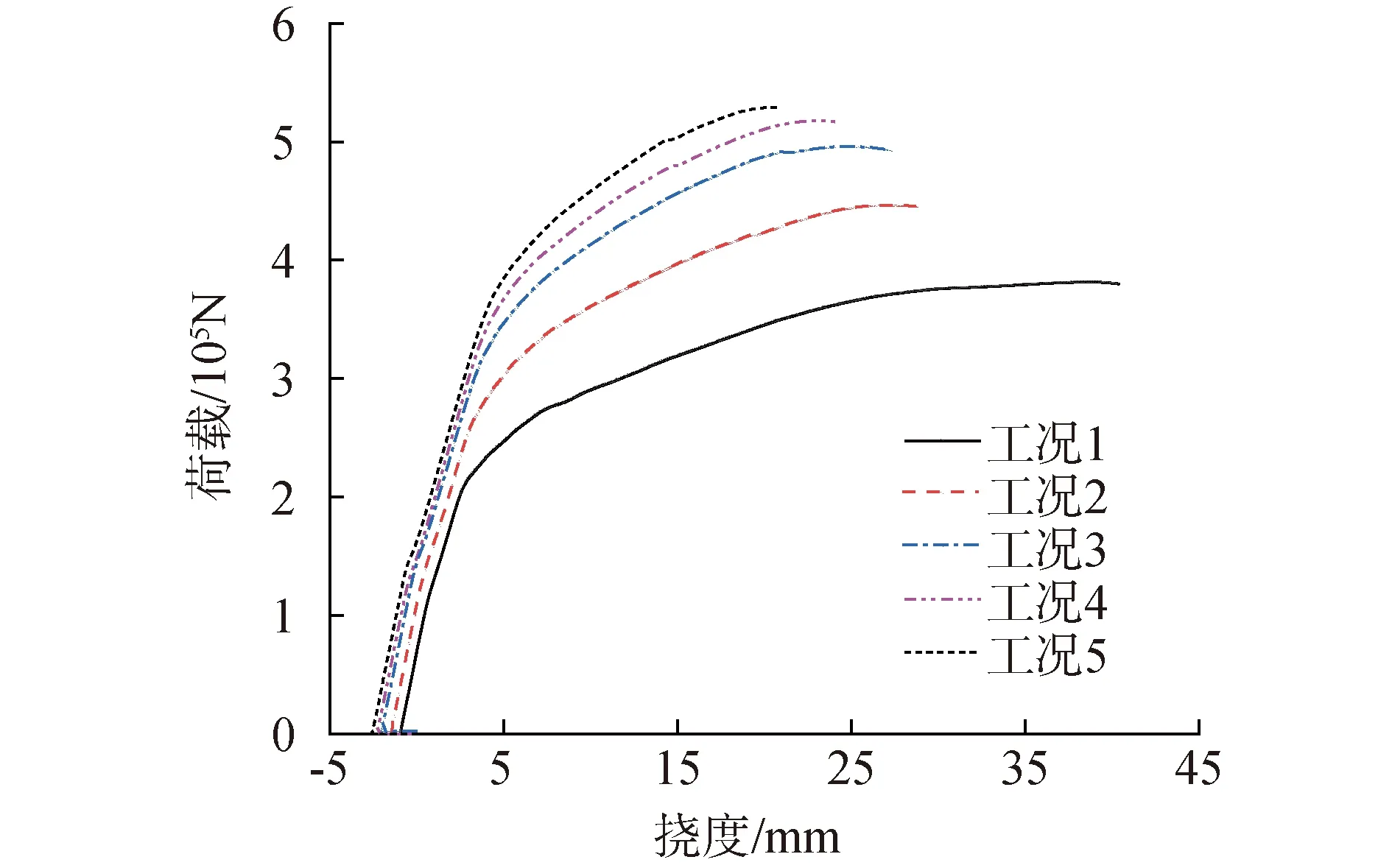
图14 不同预应力筋数量下荷载-挠度曲线Fig.14 Comparison of load-deflection curves among different numbers of prestressed tendons

3.3 接缝粘结失效面积影响分析

分段预制拼装PC盖梁进行拼接施工时,为避免环氧树脂粘结剂进入预应力孔道,在涂抹粘结剂时会在接缝界面做一定的留白处理。为保证界面粘结质量,往往需要对接缝表面进行凿毛处理,然而凿毛处理后可能会导致粘结面局部脱空。

为模拟实际拼接施工中接缝界面粘结剂局部脱空现象对结构受力性能的影响,本文共设置3个分析工况,并假设粘结失效面积均位于牛腿上部接缝,下部接缝粘结良好,各分析工况假设的粘结失效面积如图15所示,其余设计参数与NT1模型相同。

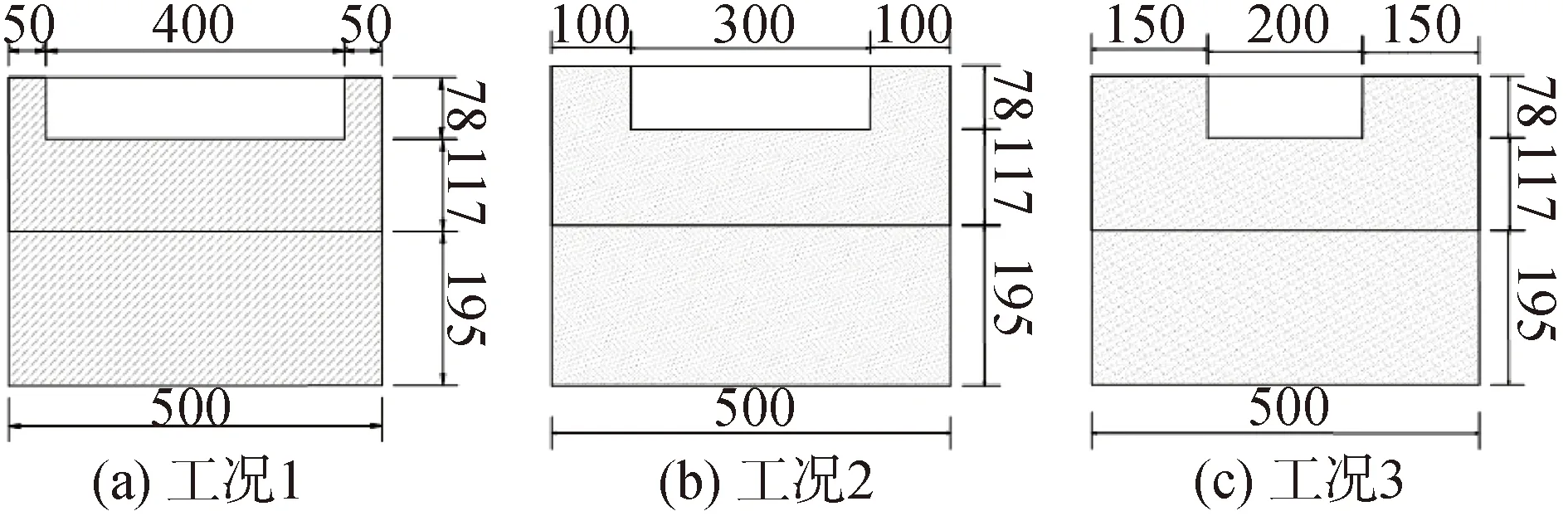
图15 接缝界面粘结失效面积分析工况Fig.15 Cases of different bond failure areas at joint interface

表2列出了不同分析工况下的有限元计算结果,表中“裂缝宽度”取为荷载达250 kN时梁体的最大裂缝宽度。可以看出,接缝界面粘结失效面积越大,开裂荷载、裂缝宽度和极限承载力均越小。此外,粘结失效面积对开裂荷载、裂缝宽度均有较大影响,而对极限承载力的影响不大。建议在有可靠措施避免环氧树脂粘结剂进入预应力孔道的前提下,增加环氧树脂粘结剂用量,使牛腿接缝有多余的环氧树脂粘结剂被挤出,以减小粘结失效面积。

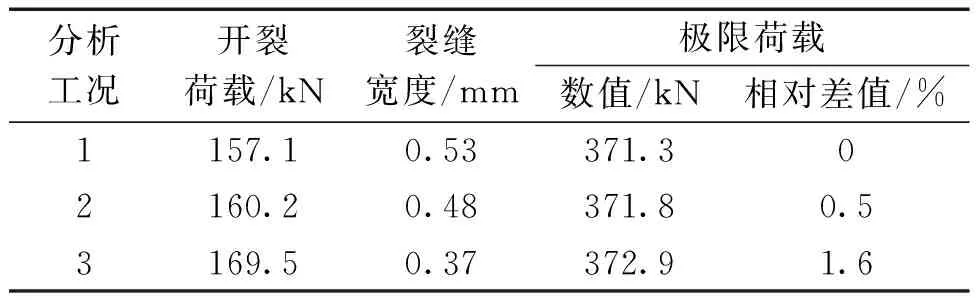
表2 不同粘结失效面积下有限元计算结果Table 2 FE results under cases of different bond failure areas

3.4 盖梁截面尺寸影响分析

由试验结果可知,NT1模型的极限承载力仅为ZT0模型的84%。为提高牛腿式接缝分段预制拼装PC盖梁的承载力,除了增加预应力筋数量外,还可增大盖梁的截面尺寸。本文分别以梁高、梁宽为变量,分别设置了3种分析工况,如图16所示,其余设计参数与NT1模型相同。

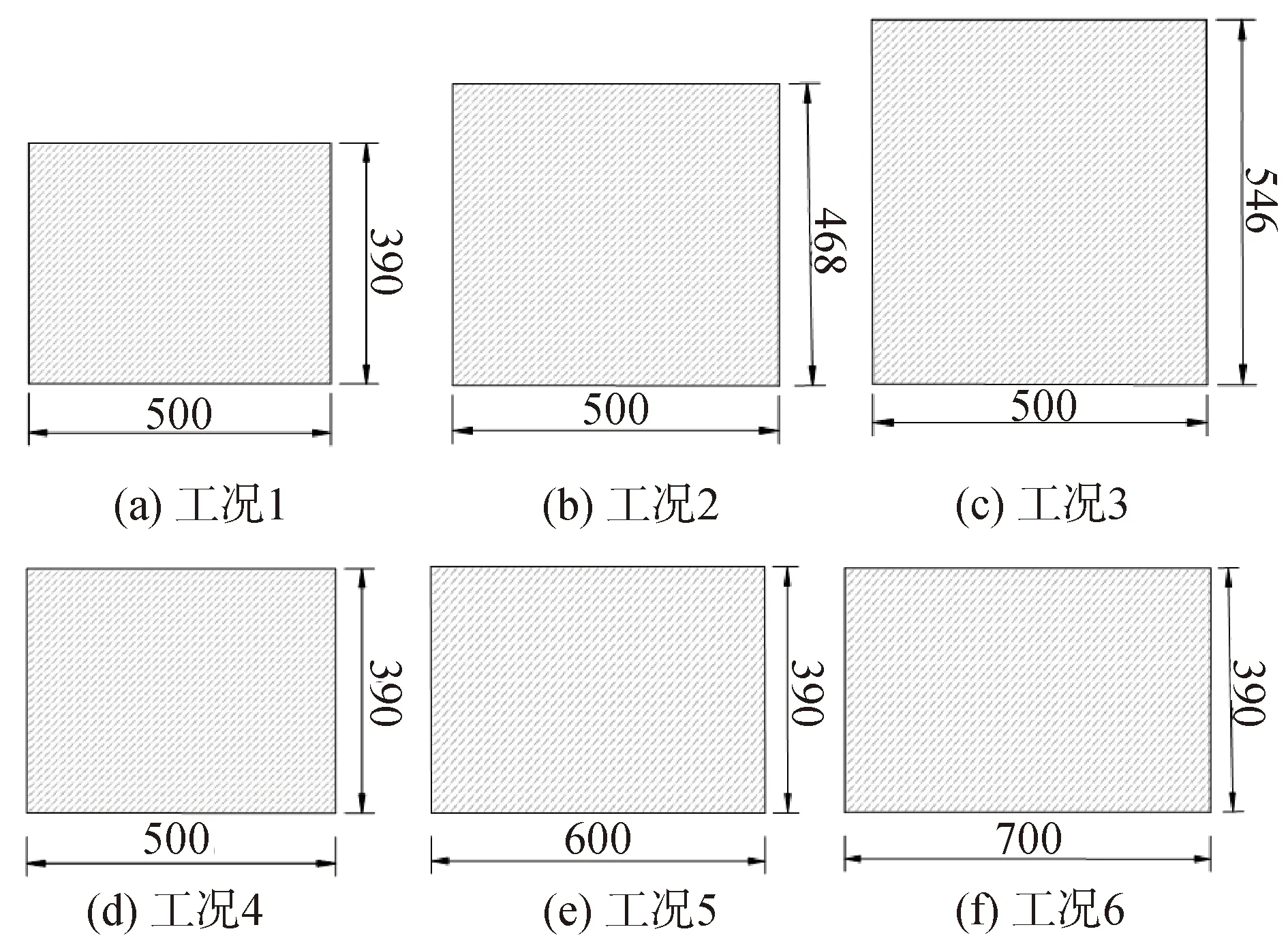
图16 截面尺寸分析工况Fig.16 Cases of different section dimensions

图17给出不同分析工况下盖梁加载点位置的荷载-挠度曲线,可以发现,随着梁高或梁宽的增大,牛腿式接缝分段预制拼装PC盖梁的开裂荷载和极限承载力均相应增大。与工况1相比,工况2和工况3的极限承载力分别提高了11.2%和28.2%;与与工况4相比,工况5和工况6的极限承载力分别提高了5.7%和9.4%。可见,增大梁高可明显提高其极限承载力,而增大梁宽对其极限承载力的提高幅度相对较小。

图17 不同截面尺寸下荷载-挠度曲线比较Fig.17 Comparison of load-deflection curves among different section dimensions

4 结论

1)与整体预制PC盖梁模型相比,牛腿式接缝分段预制拼装PC盖梁模型的极限承载力和极限变形能力均有明显下降,但其开裂荷载和破坏形态基本相同。

2)接缝界面是牛腿式接缝分段预制拼装PC盖梁的薄弱环节,破坏时接缝界面内侧的主裂缝宽度较大,受拉区混凝土完全分离,采用cohesive粘性接触单元模拟牛腿接缝的有限元模型的计算结果与试验结果吻合良好。

3)牛腿接缝位置对初始刚度和开裂荷载基本没有影响,接缝越靠近悬臂根部,盖梁的极限承载力越低。接缝设置应综合考虑减轻盖梁的最大吊重与极限承载力之间的冲突。

4)增加预应力筋数量或增大盖梁截面高度,均是提高牛腿式接缝分段预制拼装PC盖梁极限承载力的有效措施。