设置摇摆-自复位桥墩和黏滞阻尼器的斜拉桥纵向减震性能

王德斌, 郭宇晨, 孙治国

(1.大连交通大学 土木工程学院,辽宁 大连 116028; 2.防灾科技学院 中国地震局建筑物破坏机理与防御重点实验室, 北京 101601)

强震作用下,漂浮或半漂浮体系的斜拉桥易因主梁纵桥向较大的变形引发与相邻跨引桥的碰撞破坏,成为斜拉桥抗震设计的难点[1-5]。对斜拉桥纵向抗震理论的研究及相关工程实践表明,在斜拉桥塔、梁结合位置设置纵向黏滞阻尼器可以有效减少主梁纵向位移,改善结构的受力状态,同时黏滞阻尼器由于是速度相关型消能器,正常使用状态下不提供附加刚度,允许桥梁因温度变化发生缓慢的变形,在斜拉桥的抗震设计中备受青睐。Martínez等[6]以1988年Saguenay地震中发生破坏的钢斜拉桥抗震加固为例,通过数值分析手段研究了纵桥向采用阻尼器和隔震技术后桥梁的地震反应,推荐了采用黏滞阻尼器的加固方案。Jiang等[7]将负刚度装置与液体黏滞阻尼器共同应用于斜拉桥体系,在控制桥面纵向位移的同时,消除了塔底弯矩和剪力增大的不利影响。Xu等[8]提出了确定双塔斜拉桥黏滞阻尼器参数的简化方法,通过振动台分析试验,建立了黏滞阻尼器等效阻尼比的经验公式。Shi等[9]提出了黏滞阻尼器的等效线性模型,建立了布设黏滞阻尼器的漂浮体系斜拉桥地震响应简化分析方法。Xu等[10]提出了基于等效阻尼比和线性化的非线性黏滞阻尼器简化模型,推导出了斜拉桥非线性黏滞阻尼器阻尼系数的解析公式,为斜拉桥非线性黏滞阻尼器的参数选择提供了理论依据。沈文爱等[11]通过对黏滞阻尼器的阻尼系数C和速度指数α进行参数敏感性分析,得出了设置纵向黏滞阻尼器能够显著减小双座串联斜拉桥的纵向位移响应和主梁碰撞概率的结论,并给出了黏滞阻尼器的最优参数取值。近年来,桥梁抗震设计理念逐步由抗倒塌设计向功能可恢复设计方向发展,摇摆-自复位(rocking self-centering,RSC)桥墩应运而生。学者们针对RSC桥墩的建模方法以及桥墩体系结构的改进展开了深入研究。孙治国等[12]提出了RSC桥墩的数值模拟方法,并与其他学者的拟静力加载试验结果进行对比,验证了其数值模型的准确性,为布置RSC桥墩的桥梁结构进行数值分析提供了理论基础。在此基础上,其提出RSC双层桥梁排架墩抗震体系[13],得出了其在近断层地震动下的地震响应规律,为具有可恢复功能的双层桥梁的抗震设计提供了参考和依据。贾俊峰等[14]对外置耗能器的RSC桥墩抗震性能进行研究,得出外置耗能部件具有良好的可更换性和耗能能力,且RSC桥墩的抗震性能在更换前后保持一致的结论。张育智[15]将铅芯橡胶支座及液体黏滞阻尼器与RSC高墩组合形成2种减隔震体系,其认为通过布置RSC桥墩的方法可以提高阻尼器对地震输入能量的吸收,进而降低主体结构因过高能量耗散而造成的结构损伤。

为了实现对斜拉桥纵桥向地震损伤的控制,本文提出在主梁-桥塔、主梁-辅助墩间设置黏滞阻尼器以减少主梁纵向位移反应和主塔的受力。同时为避免辅助墩的破坏,将其设计为摇摆-自复位体系,通过强震下辅助墩的摇摆-自复位特性避免其产生残余变形。为验证该新型减震体系的地震损伤控制效果,本文以某斜拉桥为例,建立其有限元分析模型,并选取5组近场地震动,进行不同地震动强度下的非线性动力时程分析,对比研究该体系对斜拉桥纵向抗震性能的影响。

1 计算模型建立

1.1 斜拉桥有限元模型

本文算例所用斜拉桥模型原始设计具体参数及基于OpenSees平台的模型建立过程见文献[16],主桥为主跨240 m的双塔空间索面斜拉桥,边跨设置3个桥墩,其跨径布置为(45+42+58+240+58+42+46.5=531.5 m)。索塔采用椭圆形,向岸侧倾斜35°,塔底标高2.5 m,塔顶标高85.0 m,塔斜向高102.464 m。索塔顺桥向宽度5 m,椭圆形索塔横桥向宽度由塔顶的6.2 m渐变至塔中部的4.6 m,再渐变至塔根的9.766 m,塔柱采用六边形横断面。6#、7#、10#、11#辅助墩墩高14 m,主梁为扁平流线形封闭钢箱梁,斜拉索采用高强度钢绞线拉索,上部结构采用纵向漂浮支承体系,主梁与桥塔、各墩之间通过纵向滑动支座约束主梁竖向位移并限制其横向位移。

黏滞阻尼器作为一种速度相关型阻尼器,当加载速度较慢时,阻尼器几乎无内力产生,且其不为结构体系提供附加刚度,对结构的动力特性并无影响。当受到地震、强风作用时,由于加载速度快,阻尼器内力迅速增加,并有效吸收地震输入能量。鉴于上述特点,本文选用黏滞阻尼器作为辅助减震装置将其布置于塔梁与墩梁之间,并将6#、11#辅助墩设为摇摆墩,以便为斜拉桥组合减震体系提供复位力。斜拉桥组合结构体系及阻尼器布置情况如图1所示。

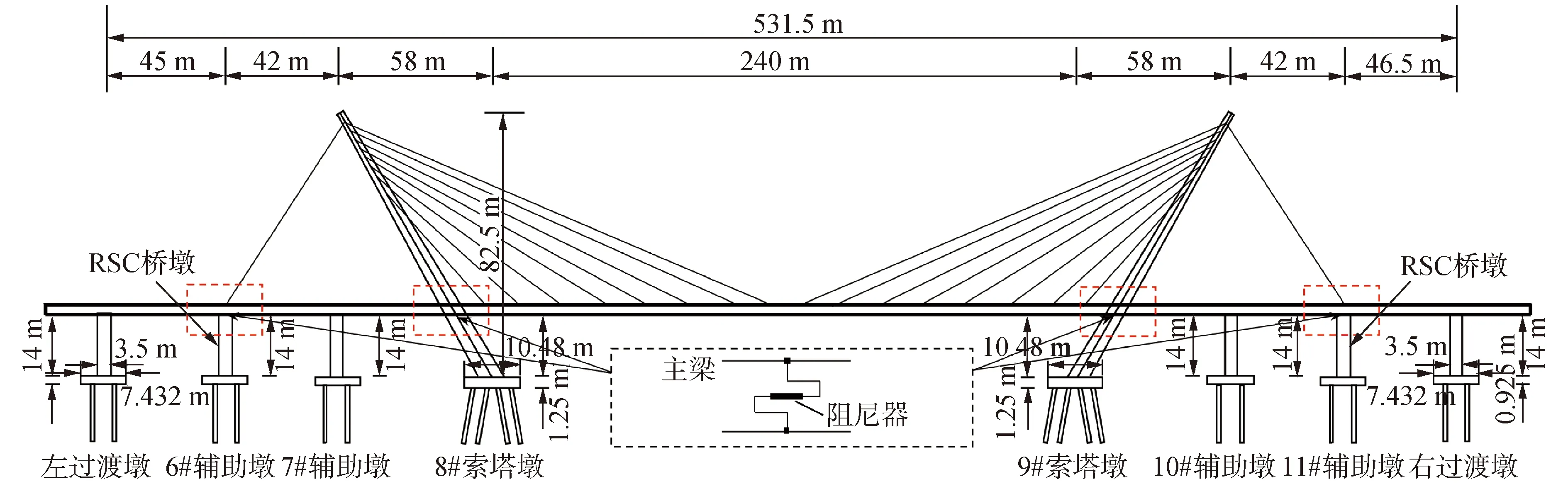
图1 斜拉桥立面图Fig.1 Elevation view of the cable stayed bridge

1.2 RSC桥墩数值模型

依据文献[15]的建模方法建立摇摆墩模型。墩身选用纤维梁单元模拟,通过零长度截面转动弹簧单元配以只受压不受拉弹性本构材料模型模拟RSC桥墩的摇摆反应。无粘结预应力钢筋采用Truss单元进行模拟,单元划分与墩身单元划分保持一致。无粘结预应力筋采用OpenSees中的Elastic-PP材料模型模拟,通过施加初应变的方法提供初始预应力,本文所用预应力筋在其最大应力达到0.8倍极限强度时认定失效[17]。无粘结预应力筋的底部节点固结,顶部节点与墩身顶部节点通过刚臂单元连接,其余节点的水平向自由度与墩身节点耦合,竖向自由运动。耗能钢筋选用Steel02单轴材料本构模型,采用Truss单元模拟,底部接缝处设置为无粘结状态,单元长度取为无粘结段长度。耗能钢筋底部节点固结,顶部节点与墩身节点通过刚臂单元连接,以此保证构件之间的协同变形。通过纤维截面来模拟零长度截面转动弹簧单元并赋予Elastic-No Tension材料本构模型对接缝处进行模拟,通过底部受压时截面两端的应变差模拟RSC桥墩的摇摆响应,RSC桥墩模型及材料本构模型如图2所示。

1.3 黏滞阻尼器数值模型

本文液体黏滞阻尼器采用OpenSees中的twoNodeLink单元进行模拟,其在桥梁中的布置情况、节点位置和坐标系如图3所示。通过定义单轴Viscous材料的阻尼系数及速度指数来赋予单元的材料属性,其力学模型为:

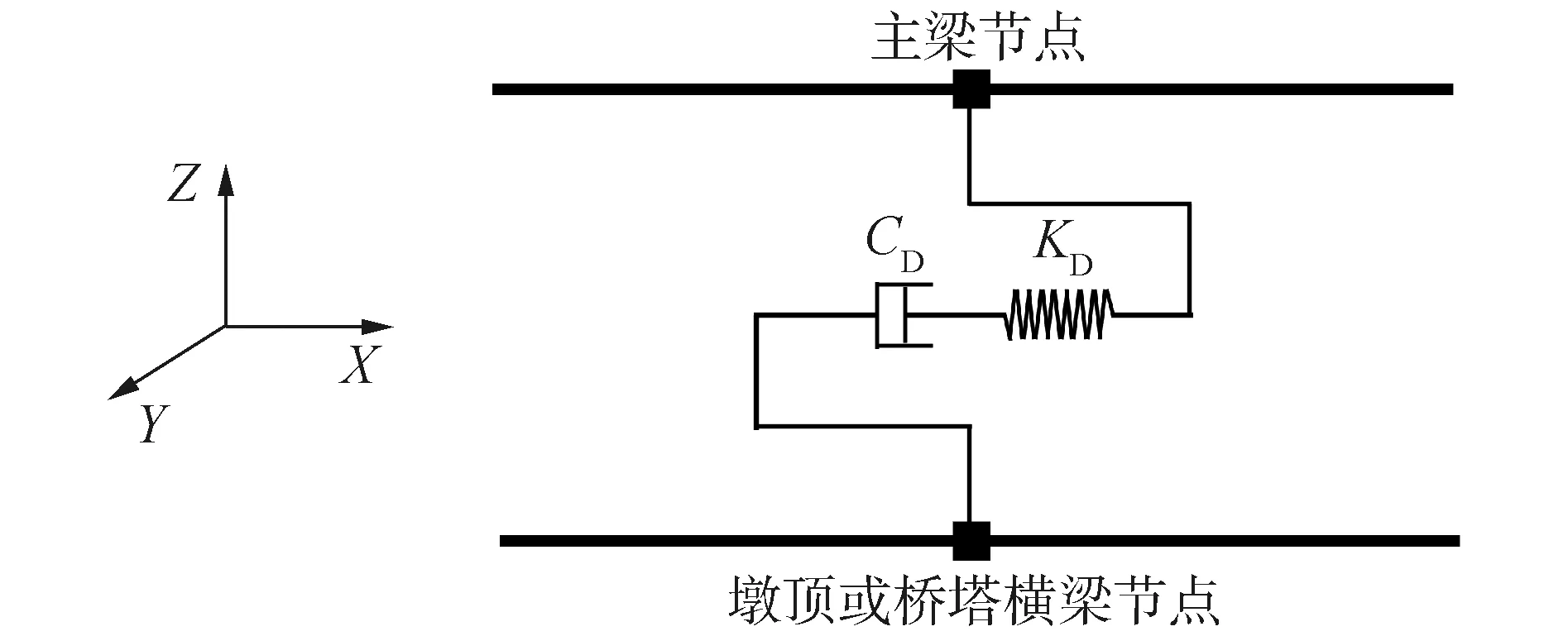
图3 黏滞阻尼器布置方式Fig.3 The arrangement of viscous dampers

Fv=CVα

(1)

式中:Fv为阻尼力;C为阻尼系数;V为阻尼器两端点的相对速度;α为速度指数。

通过对非线性黏滞阻尼器的力学特性分析可知,其阻尼系数C以及速度指数α是控制黏滞阻尼器性能的2个关键参数。桥梁工程中黏滞阻尼器的速度指数取值一般为0.3～2.0[18]。根据文献[15],本文取C=3 162 kN·(s/m),α=0.5,将黏滞阻尼器进行纵向布置,使其单独进行减震或与RSC桥墩构成组合减震体系。

2 地震动选择及工况设置

2.1 地震动选择

鉴于近断层地震动中包含丰富的长周期高能量脉冲,易造成结构产生较大的变形乃至破坏,明显增大减隔震桥梁的位移需求,本文选择近断层地震动进行分析以期获得在更不利地震动输入下斜拉桥地震响应的估计。从太平洋地震工程研究中心强震数据库选取5组近场脉冲型地震动,每组地震动包含3个平动方向的地震动数据,相关地震动记录信息见表1。由于斜拉桥在不同桥向具有明显不同的响应特点[19],本文仅选择地震动的平行断层分量对斜拉桥进行地震动输入,研究组合减震体系对斜拉桥纵向抗震性能的影响。将地震动的峰值加速度(peak ground acceleration,PGA)分别调至0.2g、0.4g和0.6g,对3种模型下的桥梁结构体系进行设计地震、罕遇地震以及巨震[20]作用下的抗震性能研究。本文结构阻尼比取为5%,选取的地震波反应谱曲线如图4所示。

表1 选取的地震动记录Table 1 Selected ground motion records

图4 地震动反应谱Fig.4 Response spectra of the selected ground motions

2.2 工况设置

本文共设计3种分析模型:模型1为斜拉桥原桥模型;模型2在6#和11#辅助墩墩顶与主梁之间、左右桥塔与主梁之间各水平布置1个黏滞阻尼器;模型3在墩梁和塔梁之间水平布置黏滞阻尼器的基础上,将6#和11#辅助墩调整为RSC桥墩,如图5所示。

图5 桥梁计算模型示意Fig.5 Sketch of the bridge calculation model

各工况下桥梁模型均进行0.2g、0.4g和0.6g下地震动输入,通过不同强度下的非线性时程分析结果获取结构关键构件的响应均值进行抗震性能分析。同时,为研究组合结构减震体系的残余变形及阻尼器耗能变化情况,本文将对桥梁体系关键部位残余位移及阻尼器耗能情况进行分析。

3 桥梁地震响应及自复位特性

3.1 减震性能分析

为研究黏滞阻尼器和RSC桥墩组合减震体系对斜拉桥纵向抗震性能的影响,本文分别对主梁纵向位移、6#辅助墩墩顶纵向位移和墩底纵向弯矩、左塔塔顶纵向位移和塔身纵向弯矩、墩梁相对位移以及塔梁相对位移的峰值进行计算,对各工况下地震响应取均值作为分析依据,计算结果见表2和表3。同时,为进一步研究组合减震结构体系的减震效果,以模型1各性能指标值作为基准值,计算模型2和模型3各关键性能指标的减震率[21],图6给出了不同地震动强度下模型2和模型3各性能指标的峰值位移减震率。

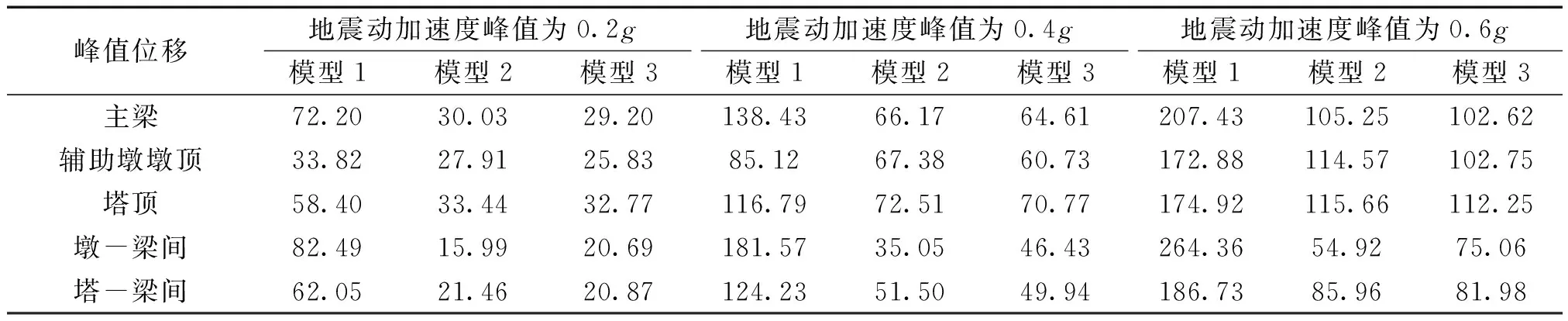
表2 峰值计算结果平均值Table 2 Average value of peak calculation results mm

表3 内力计算结果平均值Table 3 Average value of internal force calculation results

图6 不同峰值加速度下地震响应峰值减震率Fig.6 Peak damping ratio of seismic response under different peak accelerations

基于表2和图6可知,主梁纵向位移、塔顶位移和塔梁相对位移的减震效果体现出大致相同的特征。以主梁纵向位移为例,设计地震(0.2g)作用下,模型2和模型3相对于模型1的减震率分别为58.41%和59.56%;罕遇地震(0.4g)作用下,减震率分别为53.19%和54.32%;巨震(0.6g)作用下的减震率为50.26%和51.53%。由此可见,2种模型下主梁纵向位移的减震率均可达到50%以上,减震效果明显。模型3相对于模型2而言,其减震效果变化不大,减震率增幅值均在2%以内。可见,将辅助墩调整为RSC桥墩后虽然降低了主梁纵向位移,但其作用效果十分有限。同时,模型2和模型3相对于模型1的减震率随着地震动强度的增大逐渐减小,这表明模型2和模型3对改善模型1纵向减震性能的能力随着地震动强度的增大而有所降低。

墩梁相对位移呈现出不同特征,设计地震(0.2g)、罕遇地震(0.4g)和巨震(0.6g)作用下模型2相对于模型1的减震率分别为80.61%、79.69%和79.22%,可见在桥墩与主梁之间布置黏滞阻尼器可显著降低墩梁相对位移,达到了较好的减震效果。针对模型3,将辅助桥墩调整为RSC桥墩后,由于弱化了底部基础并解除了转动约束,使得墩梁相对位移显著增大,不同峰值加速度下分别增大了4.7、11.38和20.14 mm,相对于模型1位移增幅百分比分别为29.39%、32.47%和36.67%。RSC桥墩可通过墩梁相对位移增大实现阻尼器更大的位移输出,将地震动能量转化为阻尼器的黏滞耗能,进而降低主体结构的非弹性变形耗能。

由表3可知,墩底纵向剪力和纵向弯矩在未加入阻尼器时(模型1)均小于屈服值,模型2与模型1相比,墩底纵向剪力和纵向弯矩发生不同程度的减小,可见在墩梁之间布置黏滞阻尼器对墩底的剪力和弯矩具有较好的控制效果。模型3与模型2相比,墩底纵向剪力和纵向弯矩略有增大,这是由于RSC桥墩中铺设的预应力筋使得桥墩内部应变能增大,继而导致桥墩底部的内力也相应增大。与此同时,二者增幅均控制在10%以内且均小于初始屈服值。可见,RSC桥墩在保证其自复位性能的情况下,其内力增幅均在可控范围内,不会产生屈服破坏。

塔底纵向剪力和纵向弯矩在未加入阻尼器时(模型1)同样均小于屈服值,模型2与模型1相比,二者发生不同程度的减小,可见在塔梁之间布置黏滞阻尼器对塔底的剪力和弯矩具有较好的控制效果。模型3与模型2相比,塔底纵向剪力和纵向弯矩并未发生明显变化,由此可见,RSC桥墩对桥塔的剪力和弯矩不会产生明显影响。

从表2可以看出,辅助墩墩顶纵向位移在设计地震(0.2g)作用下,模型2相对于模型1的减震率为17.48%,模型3作用下减震率增至23.63%,表明RSC桥墩增强了对墩顶纵向位移的控制效果。随着地震动强度的增大,其减震率逐渐增加,巨震(0.6g)作用时,减震率最高可达40.57%。可见,相较于其他性能指标,该组合减震体系对墩顶纵向位移的减震效果均处于较低水平,这是由于在辅助墩和主梁间布置黏滞阻尼器增强了墩梁之间的固结作用,增大了辅助墩的内力输入,从而在一定程度上削弱了其对辅助墩墩顶位移的减震效能。进而也说明,仅靠辅助墩墩顶位移的峰值指标并不能完全表现出辅助墩墩顶位移的变化规律,还需从自复位性能的角度出发,对其震后残余变形进行分析。

3.2 残余位移

结构在强震作用下进入非线性阶段会产生不可恢复的永久位移或残余变形,结构残余位移是震后结构抗震性能和地震损失评估的重要参数。为进一步分析RSC桥墩的自复位特性,本文将地震波持时延长一定时间,并将加速度值取为零,桥梁体系在原持时结束后进行自由振动,由于阻尼的存在,体系的位移最后趋于稳定状态,并将此位移作为体系的残余位移。对于本文选取的地震波,经过多次试算,持时延长值统一取为10 s。考虑到地震动的随机性,对5条地震波分别计算各响应指标残余位移,然后取其平均值。不同模型下各地震响应关键指标的震后残余位移随地震动强度的变化曲线如图7所示。

图7 不同峰值加速度下地震响应残余位移Fig.7 Residual displacement of seismic response under different peak accelerations

从图7可以看出,主梁残余位移、塔顶残余位移、墩梁相对残余位移以及塔梁相对残余位移的变化规律基本一致,设计地震(0.2g)作用下,模型1各性能指标震后残余位移值均在8 mm以上,随着地震动强度的增大,震后残余位移逐渐增大,巨震(0.6g)时达到最大,各性能指标残余位移值均在30 mm以上。可见,原桥模型在不同强度的地震输入下,各性能指标均存在不同程度的较大残余位移,桥梁自复位性能较差。模型2下各性能指标震后残余位移显著降低,巨震(0.6g)作用下各性能指标残余位移值均小于3 mm,减震率达到90%以上,自复位效果显著。模型3相比于模型2,各性能指标的震后残余位移值进一步降低,几乎接近于零,表明该组合减震体系具有更佳的自复位性能。

辅助墩墩顶的残余位移呈现出不同变化规律,罕遇地震(0.4g)下模型1的残余位移值为1.65 mm,模型2与模型1相比,震后残余位移值显著增大,最大为4.45 mm,这是由于在辅助墩和主梁之间安置黏滞阻尼器导致墩梁相互连接作用加强的影响,墩顶位移表现为减震效能的削弱,其残余位移表现为随之显著增大。模型3的残余位移值减小为1.01 mm,相较于模型1降低了38.8%,相较于模型2降低了77.3%,可见RSC桥墩可显著降低辅助墩顶残余位移,具有良好的自复位特性。巨震(0.6g)作用下,模型1的残余位移值为4.47 mm,模型2的残余位移值增至8.73 mm,增幅为95.3%,模型3的残余位移值则减小为1.75 mm,相较于模型1降低了60.85%,相较于模型2降低了79.95%,可见随着地震动强度的增大,RSC桥墩体现出更强的自复位性能。

为进一步分析辅助墩墩顶残余位移,图8给出了3种模型在PGA为0.6g作用时Cape Mendocino地震波作用下的辅助墩墩顶位移时程曲线,可以看出模型1墩顶位移响应整体较大。与模型1相比,模型2时程曲线更为平稳,位移显著降低,但二者震后残余变形明显,墩顶位移在地震动后期均偏离平衡位置,无法恢复到初始平衡状态。模型3位移时程曲线与模型2相近,墩顶位移大幅降低,同时其位移时程曲线始终在平衡位置上下波动,震后残余位移几乎为零,桥墩可恢复到其初始平衡位置,体现了RSC桥墩良好的自复位性能。

图8 Cape Mendocino波作用下墩顶位移时程曲线Fig.8 Time history curves of pier tip displacement under Cape Mendocino wave

3.3 阻尼器耗能

将辅助墩更换为RSC桥墩后,墩梁相对位移峰值指标显著增大,为研究墩梁之间黏滞阻尼器的耗能变化,以Loma Prieta地震波为例,图9给出了不同峰值加速度下6#桥墩与主梁之间黏滞阻尼器的荷载-位移滞回曲线。

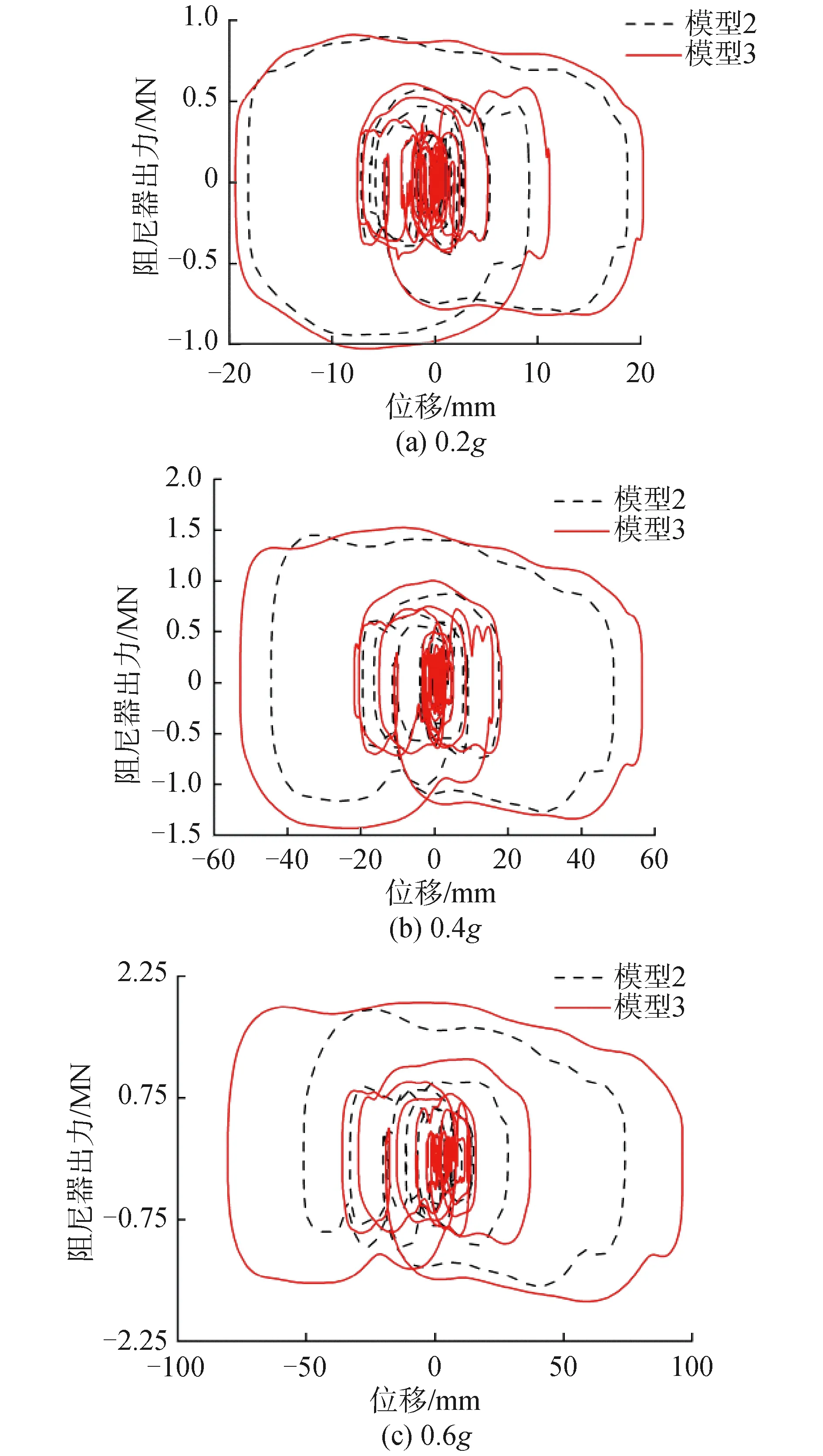
图9 Loma Prieta波作用下阻尼器滞回曲线Fig.9 Hysteresis curves of dampers under Loma Prieta waves

从图9可以看出,Loma Prieta地震波作用下6#桥墩与主梁之间的黏滞阻尼器具有稳定的滞回性能,滞回环的形状饱满近似为椭圆形,可见本文所选用的黏滞阻尼系数为3 162 kN·(s/m),速度指数为0.5的非线性黏滞阻尼器对输入的地震能量进行了充分耗散,能够对桥梁的纵向地震响应起到很好的控制效果。黏滞阻尼器在设计地震(0.2g)作用下,模型2的最大输出荷载为941.8 kN,最大输出位移为18.7 mm,模型3最大输出荷载为1 026.5 kN,较模型2增加9%,最大输出位移为20.2 mm,较模型2增加8%,可见将原桥辅助墩调整为RSC桥墩后阻尼器输出荷载和输出位移均有所增大。罕遇地震(0.4g)作用下,模型2最大输出荷载1 451.7 kN,最大输出位移为48.8 mm,模型3最大输出荷载为1 526.1 kN,较模型2增加5%,最大输出位移可达56.6 mm,较模型2增加15.98%。巨震(0.6g)作用下,模型2最大输出荷载为1 836.6 kN,最大输出位移为73.9 mm,模型3最大输出荷载为1 922.5 kN,较模型2增加4.6%,最大输出位移为96.2 mm,较模型2增加30.18%。可见,模型3相比于模型2,阻尼器最大输出荷载的增幅随着地震动强度的增大而略有下降,而最大输出位移的增幅则随之显著增大,说明位移增大是阻尼器耗能增加的最主要影响因素。

为进一步研究阻尼器在不同模型下的能量耗散情况,图10给出了模型2和模型3在PGA为0.2g、0.4g和0.6g的Loma Prieta地震波作用下的阻尼器耗能随时间变化曲线。

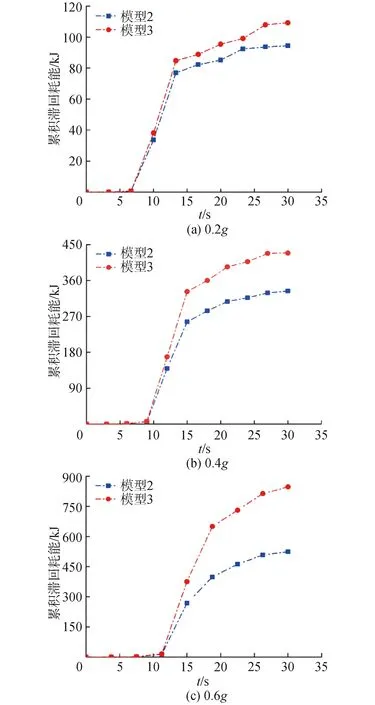
图10 Loma Prieta波作用下阻尼器耗能时程曲线Fig.10 Energy dissipation time history curves of damper under Loma Prieta wave

可以看出PGA为0.2g时,模型2和模型3耗能曲线初期平稳,几乎不耗能,此时阻尼器的输出位移处于较低水平,6 s后耗能显著增加,模型3累积耗能开始超过模型2,到14 s后曲线变缓,但模型3的耗能已明显超越模型2,两模型累积耗能差值呈显著增大趋势,地震结束时,模型2累积耗能为94.5 kJ,模型3累积耗能109.8 kJ,较模型2增加16.2%。这主要是由于RSC桥墩的设置导致墩梁相对位移增大进而增大阻尼器的输出位移,同时阻尼器的输出荷载也有所增大,在两者的共同影响下阻尼器累积耗能显著提高。PGA为0.4g和0.6g时,模型2累积耗能分别为333.6 kJ和523.5 kJ,模型3分别为435.9 kJ和846.8 kJ,模型3较模型2分别提高30.67%和61.76%。可见,阻尼器耗能伴随着RSC桥墩的设置显著增加,不同地震动强度下阻尼器的耗能基本规律保持一致,并且随着地震动强度的增加在组合减震体系的影响下阻尼器体现出更佳的耗能效果。

4 结论

1)对于设有RSC桥墩和黏滞阻尼器组合作用下的斜拉桥,其主梁纵向位移、塔顶纵向位移和塔梁相对位移均明显降低,其减震效果优于仅设黏滞阻尼器的桥梁减震体系,但总体差异并不明显,各性能指标的残余位移总体变化规律与各性能指标峰值位移的变化规律基本一致。

2)黏滞阻尼器的存在会增加其所在位置处墩梁的相对位移,并导致桥墩墩顶的震后残余位移显著增大,不利于桥墩震后快速修复,通过将辅助墩调整为RSC桥墩可有效提高墩梁相对位移,增大阻尼器的输出荷载和输出位移,提升阻尼器的累积耗能,进而避免主体结构对地震能量过多吸收所导致的损伤。

3)RSC桥墩的存在有效降低了主体结构各关键性能指标的残余位移值,相较于仅设黏滞阻尼器的减震体系,组合体系桥墩残余位移降低幅度明显,基本恢复至初始平衡状态,该减震结构体系提升了主体结构的自复位能力,能够达到桥墩震后无损或快速恢复的效果。