长大下坡道区段限速对有轨电车旅行时间影响的计算与仿真研究

杨 坚

(1.丽江雪山轨道交通有限公司,674199,丽江; 2.中铁建云南投资有限公司,650220,昆明∥高级工程师)

受地形地势影响,我国西南地区的有轨电车线路通常存在长大坡道,且有些线路的长大坡道占比很大。在丽江有轨电车1号线(以下简称“丽江1号线”)中,坡度≥30‰的长大坡道线路长9.66 km,占线路全长的47.7%,其中区间最大下坡度为-55‰。长大下坡道会增大有轨电车制动距离,进而加大有轨电车追踪距离。为保证有轨电车在长大下坡道上的运行安全,需对其进行限速,但这又会对线路的通过能力产生影响。因此,有必要研究长大下坡道区段不同限速值对区间通过能力产生的影响。

目前,对长大下坡区段限速方面的研究,主要集中在高速铁路领域。文献[1]综合考虑了高速列车常用制动限速和紧急制动限速的影响,采用合力分析法和分段累加法计算高速列车在下坡运行的限速。文献[2]对高速铁路长大下坡地段列车运行速度进行研究。文献[3]对长大下坡道条件下的高速铁路闭塞分区布置进行研究,通过构建数学模型解决高速铁路长大坡道闭塞分区布置问题。

对于长大下坡道限速对通过能力的影响,以往的研究大多为定性分析,很少有定量分析。本文按照不同坡度将线路划分为不同区段,基于有轨电车牵引计算和区间运行时间计算,定量计算长大下坡道不同限速下的最小区间旅行时间。基于最小旅行时间及运行间隔,通过Opentrack软件进行仿真,得到列车运行图,进而定量分析不同限速下的区间通过能力。

1 基于牵引计算的有轨电车运行时间计算

本文通过有轨电车牵引计算和有轨电车区间运行时间计算,基于详细的线路条件及有轨电车特性,按照不同坡度将线路划分为不同行车区段,并确定每个行车区段的长度、曲线半径、坡度、限速值;对于有轨电车,确定车辆质量、有轨电车牵引制动性能、基本阻力及其附加阻力的计算;最终求解输出长大下坡道区段的有轨电车旅行时间。

1.1 有轨电车的牵引计算

考虑到线路坡度设置对有轨电车运行速度的影响,进而对有轨电车区间运行时间产生影响,为此,按照不同坡度将线路划分为不同区段,来定量研究坡度等线路条件对有轨电车运行速度的影响。

1.1.1 有轨电车基本阻力

有轨电车基本阻力主要受有轨电车运行速度的影响,其计算式为[4]:

w0=mg(A+Bv+Cv2)

(1)

式中:

w0——有轨电车基本阻力;

A、B、C——基本阻力计算系数,按经验取常数;

v——有轨电车运行速度;

m——有轨电车的质量;

g——重力加速度。

1.1.2 有轨电车附加阻力

有轨电车在行车过程中不但受到基本阻力的作用,还受到附加阻力的作用。附加阻力与基本阻力不同,主要取决于线路条件,包括坡道附加阻力、曲线附加阻力、隧道附加阻力。有轨电车经过坡道和曲线线路时产生的阻力[5],以及有轨电车经过隧道时的附加阻力分别为[6]:

wi=mgsinα

(2)

(3)

ws=μv2

(4)

(5)

式中:

wi——坡道附加阻力;

α——线路坡度;

wr——曲线附加阻力;

ρr——线路曲线半径;

ws——隧道附加阻力;

μ——经验常数;

wf——总附加阻力。

考虑到有轨电车运行过程的复杂性,本文将有轨电车看作一个质点,依据牛顿第二定律,有轨电车的运行动力学方程可表示为:

m(1+γ)a=f-w0-wf

(6)

式中:

γ——有轨电车回转系数;

a——有轨电车加速度;

f——有轨电车牵引制动力;f>0为牵引力,f<0为制动力。

1.1.3 有轨电车的牵引制动力约束

对有轨电车在运行过程中受到的牵引制动力的限值进行约束,则有:

fmin≤f≤fmax

(7)

式中:

fmin——有轨电车最大制动力;

fmax——有轨电车的最大牵引力。

1.2 有轨电车区间运行时间计算

有轨电车区间运行时间同运行速度及区间长度有关。本文把有轨电车运行区间离散为若干区段,则有:

(8)

式中:

LΔ——离散区段长度;

tΔ——离散区段运行时间;

v1、v2——有轨电车在离散区段内运行的初速度、末速度。

1.2.1 有轨电车初末速度限制

对有轨电车运行初始速度和末速度进行约束,确保有轨电车在起点的速度v0与在终点的速度vz都为0,即:

v0=vz=0

(9)

1.2.2 线路固定速度限制

为了严格保证有轨电车在长大下坡道上的运行安全,有轨电车在线路各离散区段的运行速度都绝对不能超过该区段的限速值vmax。即:

0≤v≤vmax

(10)

1.3 基于牵引计算的有轨电车运行时间计算模型

由有轨电车牵引计算和有轨电车区间运行时间计算可得基于牵引计算的有轨电车运行时间计算模型。该模型的输入参数为m、g、γ、ρr、α、A、B、C、μ、va、vb、vmax、fmin、fmax、LΔ;决策变量为a、v、f、w0、wf、tΔ。

模型目标为最小化总旅行时间ts,约束为式(1)、式(5)—式(10)。

2 基于Opentrack的有轨电车区间运行仿真模型

2.1 线路基本条件

丽江1号线位于云南省丽江市玉龙雪山南侧山麓,南起游客中心站,北至玉龙雪山站,串联了丽江市主要旅游景区及客流集散点,是丽江城市轨道交通线网规划中的旅游快速骨干通道。丽江1号线线路全长20.465 km,共设5座地面站,分别为游客中心站、白沙古镇站、玉水寨站、东巴谷站和玉龙雪山站,平均站间距为5.052 km。

丽江1号线线路坡度基本与地面自然坡度一致,全线共设28个坡段,最大纵坡为-55.0‰(下坡)。丽江1号线有轨电车运行状态通常为持续上坡和持续下坡。丽江1号线不同坡度的坡段数量如表1所示。

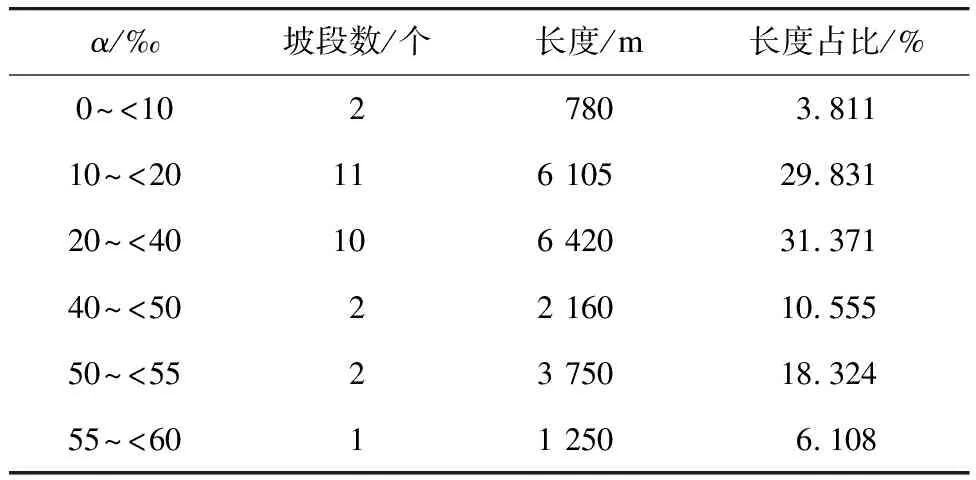
表1 丽江1号线不同坡度的坡段数量表

2.2 仿真模型的建立

本文通过Opentrack软件对该项目线路进行仿真,得到丽江1号线仿真线路图如图1所示。仿真模型的构建流程如图2所示。主要构建步骤如下:

注:深色区段为有轨电车运行占用区段,浅色区段为有轨电车开通的进路。

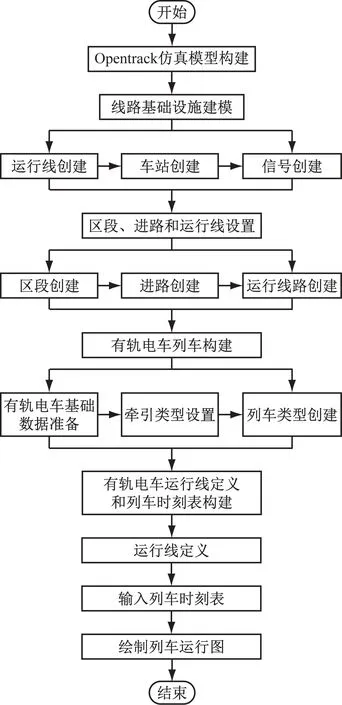
图2 仿真模型的构建流程图

1) 线路基础设施建模。该步骤还包括对线路长度、坡度、半径、限速条件、有无隧道等线路基础设施进行定义。

2) 区段、进路和运行线设置。区段是由一系列连续的双顶点和双顶点之间的轨道组成,区段的起讫点为主信号机,1个区段只能被1列有轨电车占用。进路由同一方向的1个或多个区段组成。运行路线包括1个或多个进路。

3) 有轨电车的有轨电车构建。包括车辆基础数据准备、车辆牵引类型构建及有轨电车类型构建等3个步骤。

4) 有轨电车运行线定义和时刻表构建。根据有轨电车牵引计算得到的区间运行时间及相应的行车间隔来定义某段时间(如30 min)内的有轨电车运行。其中行车间隔t间=列车周转时间/运用车列数。时刻表数据是用来定义某条运行线及其类型的。时刻表和运行线之间有着密切的关系。运行线所对应的时刻表数据包括运行线编号、车站、到站时间、离站时间和最小停站时间等。

3 线路仿真试验

3.1 线路仿真试验的数据取值

本文选取丽江1号线玉龙雪山站—东巴谷站下行方向区间(以下简称“玉东区间”) 的线路进行线路仿真试验。玉东区间线路长度为11.240 km,有整条线路中最大的坡度。根据坡度,玉东区间划分为13个行车区段,其中区段1、2、4、6、8、9、11的坡度α≥30‰。考虑行车安全需对有轨电车限速。限速方案如表2所示。

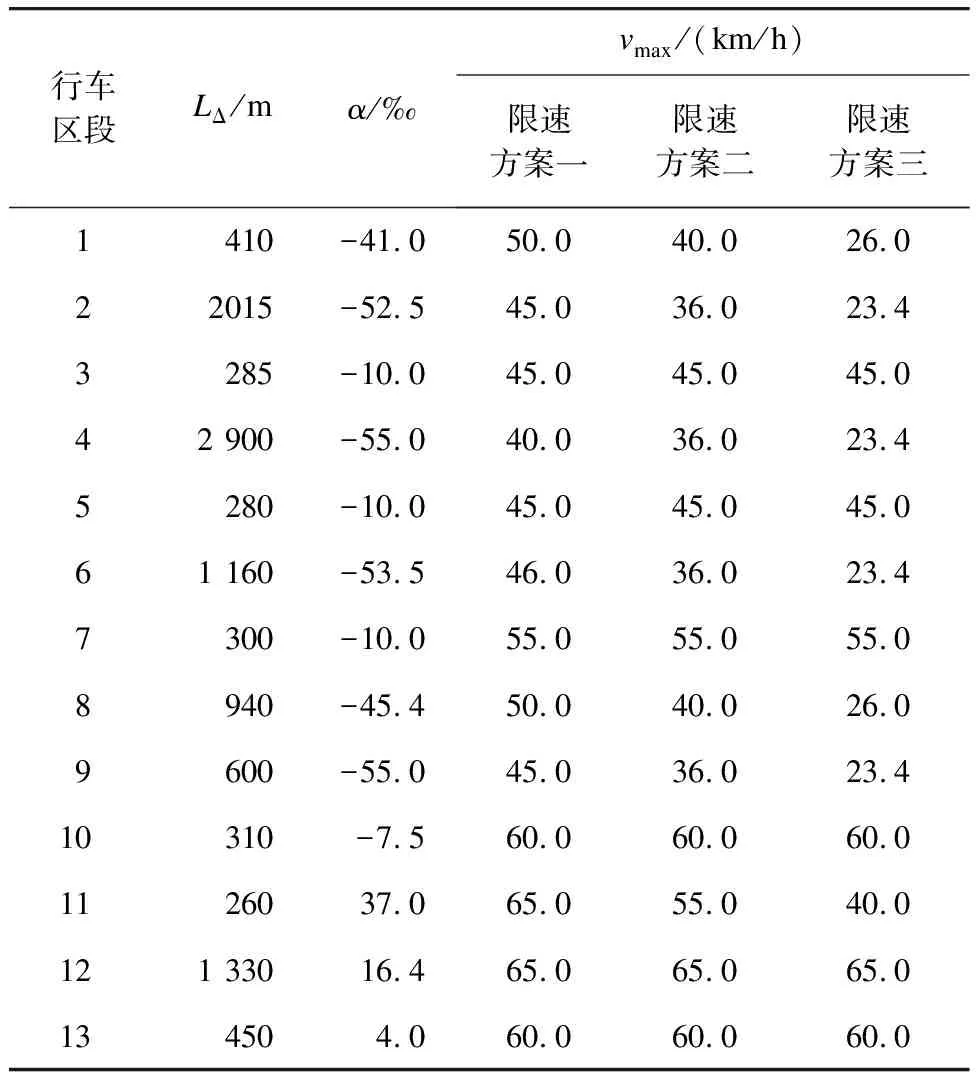
表2 玉东区间各行车区段的α和vmax

丽江1号线有轨电车的车辆参数取值为:m=65 370 kg,γ=0.061 2,A=1.02,B=0.023,C=0.000 42。计算可得,有轨电车设计最大运行速度vM=70 km/h。

3.2 线路仿真试验结果分析

本文使用IBM ILOG CPLEX12.7优化求解器对有轨电车运行时间进行求解,根据各位置处的有轨电车v及线路α绘制不同限速方案下有轨电车运行速度曲线如图3所示,牵引制动力曲线如图4所示。

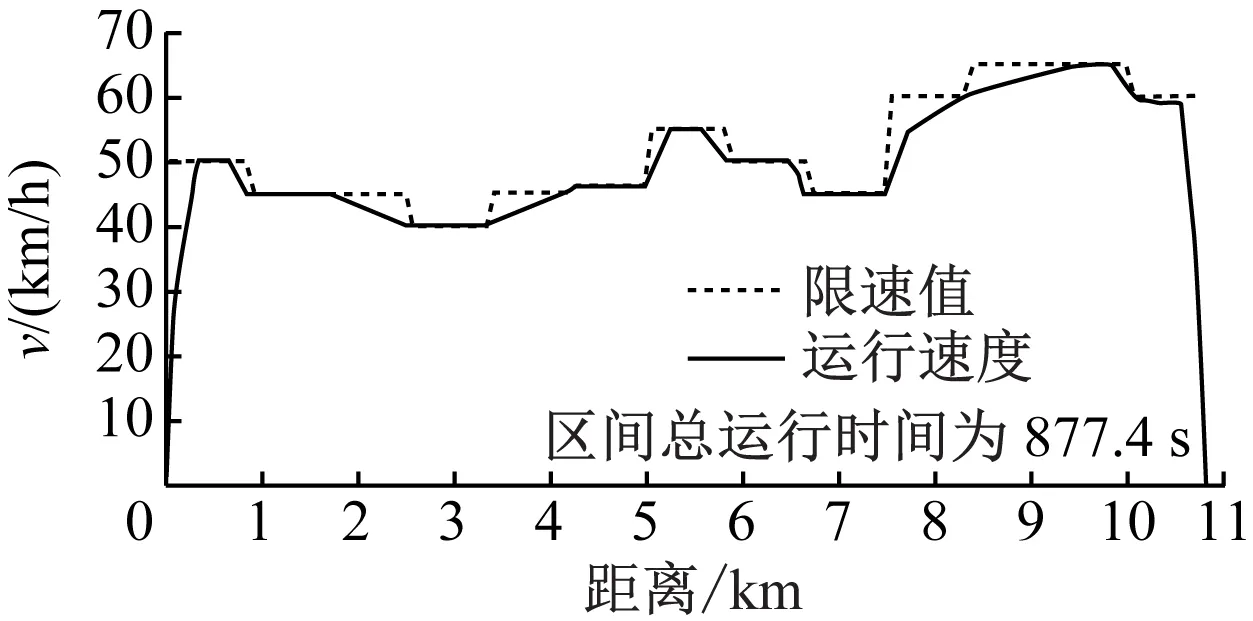
a) 限速方案一

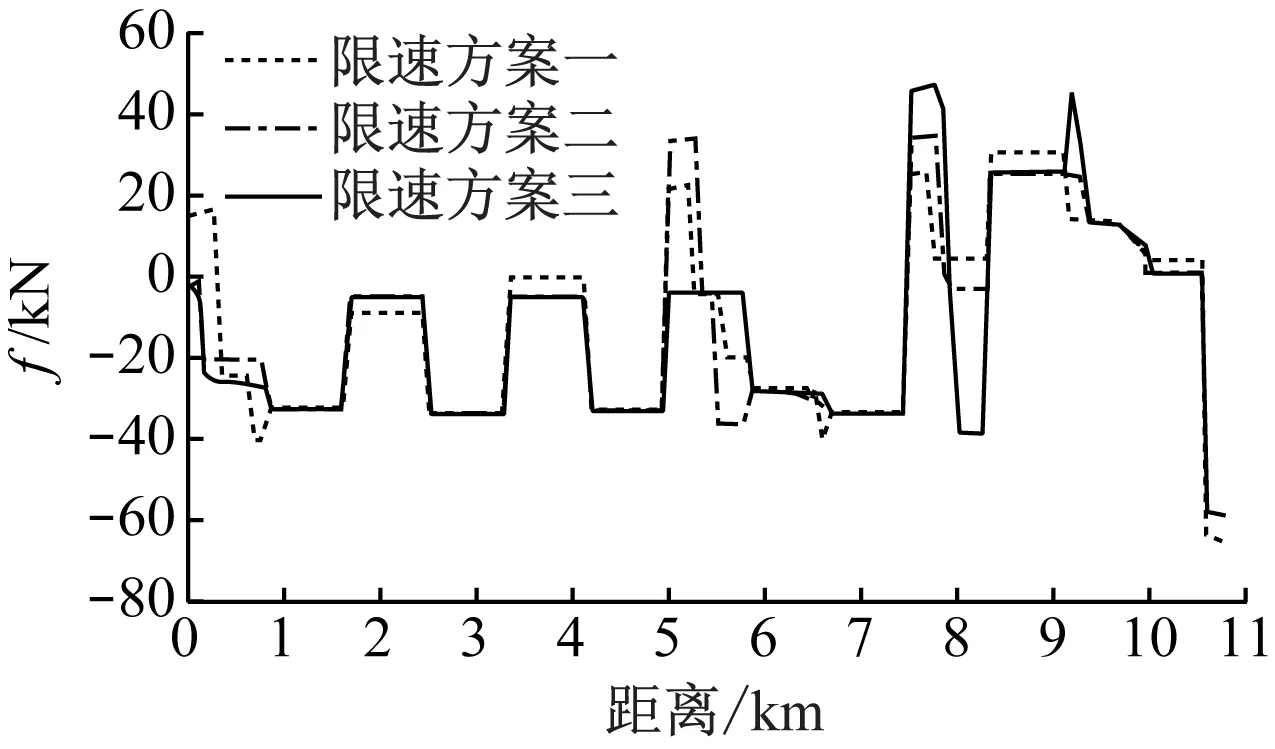
注:牵引时f为正,制动时f为负。

求解得到3个限速方案下的有轨电车区间总运行时间、区间总牵引制动力,具体如表3所示。

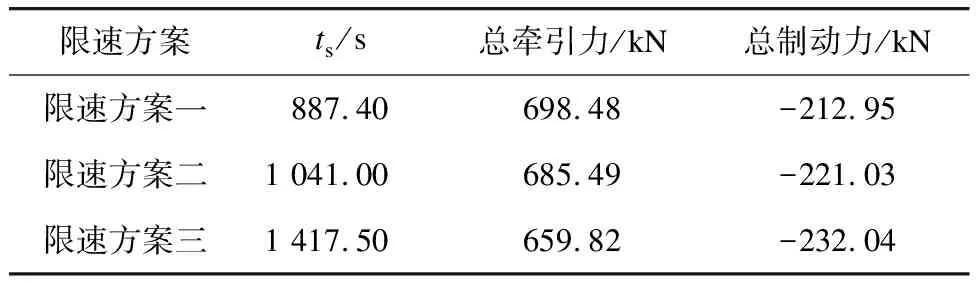
表3 不同限速方案下的有轨电车区间ts、区间总牵引力及总制动力

由表3可以看出:在确保有轨电车运行安全的前提下,当长大下坡道的限速越低时,有轨电车区间总旅行时间越长,区间总牵引力越小,区间总制动力越大。

进而,基于不同限速方案下的区间最小旅行时间,分别计算行车间隔时间。因本研究只考虑了长大下坡道不同区间限速对有轨电车在该区间内运行时间的影响,故对t间的计算进行了简化处理。

计算过程如下:分别选取不同限速方案下的区间总运行时间作为玉东区间下行方向的运行时间,其他区间运行时间沿用《丽江城市综合轨道交通项目一期工程可行性研究报告》的相关数据。经计算,不同限速方案对应的t间分别为5.5、5.7、6.0 min。

利用Opentrack软件分别对不同限速方案下的t间进行仿真分析,得到部分时段运行图。其中限速方案一的部分时段运行图如图5所示。由仿真结果可知,在限速方案一和限速方案二下,玉东区间30 min可通过6列有轨电车;在限速方案三下,玉东区间30 min可通过5列有轨电车。由此进一步计算可知,若长大下坡道的有轨电车限速vmax减小50%,则线路通过能力将降低约17%。

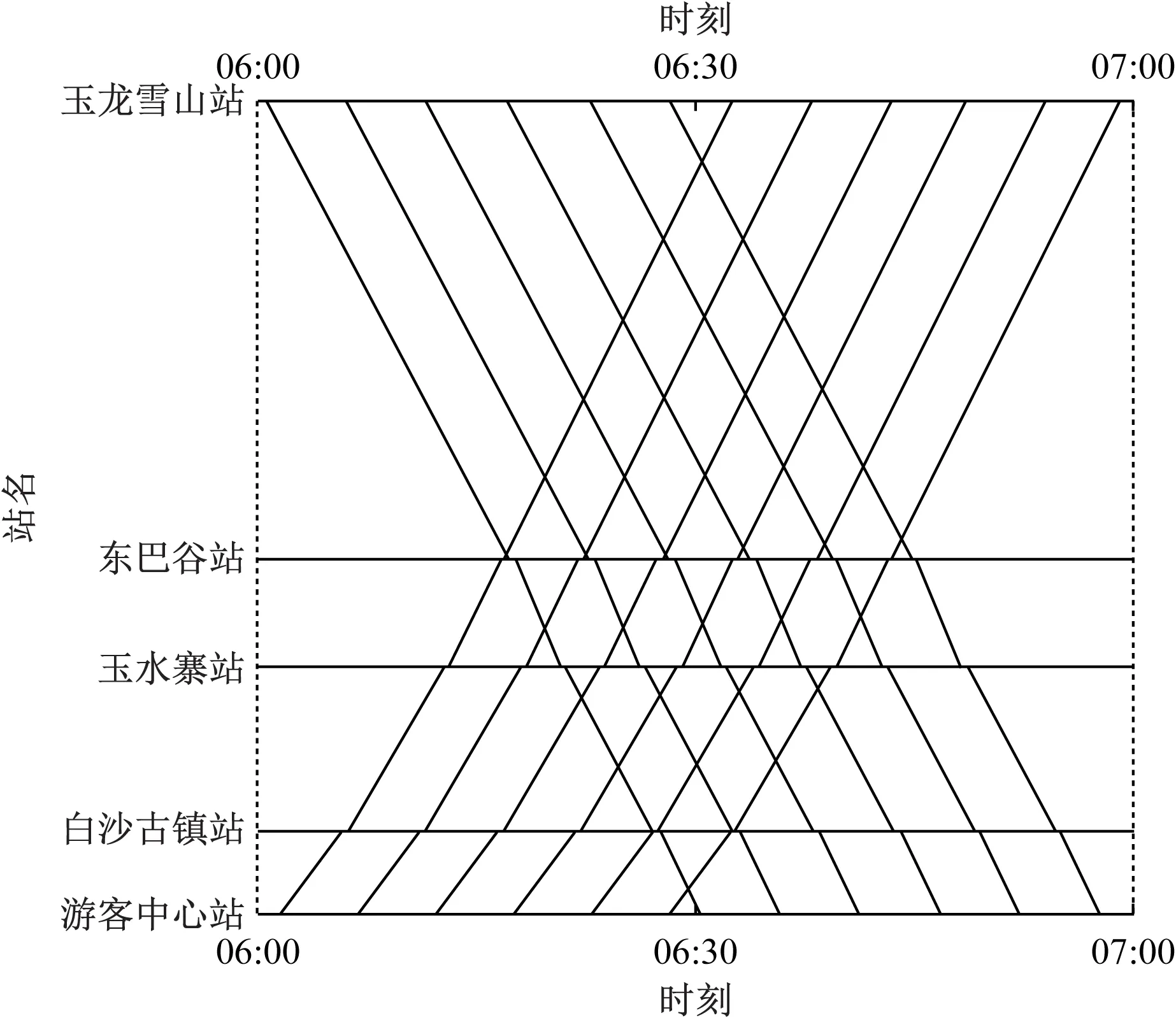
图5 限速方案一的有轨电车部分时段运行图

由试验结果可知,vmax与有轨电车通过能力呈反比关系:vmax越低,则区间运行时间越长,对应的t间也就越长,相应的线路通过能力就越低。

4 结语

针对西南地区有轨电车线路存在的坡度大、坡道长问题,往往采用区间限速来保证有轨电车在长大下坡道上的行车安全。本文基于有轨电车牵引计算及区间运行时间计算,建立区间运行仿真模型,定量分析了长大下坡道区间限速对有轨电车通过能力的影响。以丽江有轨电车1号线的线路及有轨电车数据进行实例分析。根据示例仿真分析结果分析,在确保有轨电车运行安全的前提下,长大下坡道限速减小50%,线路通过能力降低了约17%。由此总结:长大下坡道的限速方案会影响有轨电车的区间运行时间及该区段的行车间隔,进而影响该区段的线路通过能力;对长大下坡道限速越小,有轨电车区间总旅行时间越长,对应的行车间隔时间也越大,区间的通过能力就会越小。