排水桩加固及动力荷载强度对可液化地层中盾构隧道动力响应的影响*

冯 义

(中铁第一勘察设计院集团有限公司,710075,西安∥高级工程师)

隧道工程作为大型地下结构工程之一,其穿越可液化地层时面临着较大的液化破坏风险[1],随着近年来地下工程的不断发展,隧道的动力响应研究受到越来越多的关注。

文献[2]进行了饱和砂土地层中隧道结构动力离心模型试验;文献[3]针对可液化地基中车站结构周边地基的液化区分布特性及其位移矢量场,进行了数值模型分析;文献[4]针对盾构隧道穿越液化地基的动力破坏风险,进行了小型振动台试验研究;文献[5]开展了砂土地基振动台试验;文献[6]针对加拿大某沉管隧道砂土液化问题,开展了动力离心机试验。

UBC3D-PLM本构模型能很好地描述饱和土层液化特性。文献[7-11]利用该模型对可液化层的动力响应进行了研究。本文依托上海轨道交通崇明线工程(以下简称“崇明线工程”),利用Plaxis2D岩土数值模拟软件,基于UBC3D-PLM土体本构建立数值模型,分析评价排水桩加固措施的效果及范围,并探究不同动力强度下隧道穿越可液化地层的动力响应。

1 工程概况

崇明线工程线路起自上海市浦东新区金桥地区,终于上海市崇明区陈家镇,是一条快速联系崇明岛、长兴岛和上海城区的市域线,跨越长江入海口。崇明线工程的地理位置示意图如图1所示。崇明线工程线路长约40.82 km,共设8座地下站,线路设计速度为120 km/h。

图1 崇明线工程地理位置示意图

本文研究的范围为崇明线工程的崇明岛陆域段地下盾构区间(以下简称“崇明地下段”),具体范围为3#大小盾构转换井—陈家镇站—东滩站—高架起点。崇明地下段采用的盾构管片直径为6.9 m,环宽为1.5 m。崇明岛为长江入海口冲积形成,为我国第三大岛,地质条件特殊而复杂。拟建场地在20 m深度范围内有饱和的可液化砂质粉土层,面临着地震作用下的破坏及上浮等风险。

2 模型的参数选取及验证

本研究使用Plaxis2D软件来进行数值模拟,其中,可液化的砂质粉土层采用UBC3D-PLM本构模型,上覆粉质黏土层及下部黏土层采用M-C(Mohr-Coulomb)本构模型,隧道采用线弹性本构模型进行模拟。

2.1 本构模型参数的选取

材料主要参数如表1所示。

表1 材料主要参数

UBC3D-PLM模型是一个非线性弹塑性模型,能通过捕捉砂土或黏土的地震液化行为来累积塑性应变和孔隙水压力。该本构模型在本文数值模拟中所采用的其他参数按照关联公式推出。关联公式如表2所示[7,10-13]。

表2 校准参数UBC3D-PLM模型的关联公式

2.2 模型验证

本文通过对实际工程的数值模拟来验证模型的可靠性和有效性。

1971年美国加利福尼亚洲San Fernando地区发生6.6级大地震。San Fernando大坝地基场地的基岩为胶结不良的砾岩或粗粒砂岩,在地震作用下发生土体液化,导致大坝主体被破坏,出现溃坝现象。本文选择San Fernando大坝液化溃坝的实际工程案例,根据大坝实际土层和尺寸进行数值建模。

San Fernando大坝主要土层包括基岩、冲积土、水力冲填土及黏土心墙。San Fernando大坝模型尺寸如图2所示。大坝整体跨度为100 m,高度为25 m,坡度为1∶2;基岩整体长度为300 m,高度为10 m。通过在模型底部设置线位移和位移乘子来模拟大坝所受的地震作用。使用El-Centrol加速度谱施加激励,峰值加速度为0.6g(g为重力加速度)。模型两侧为自由场约束,底部为固定约束。大坝上游水位为15 m,下游水位为-1 m。

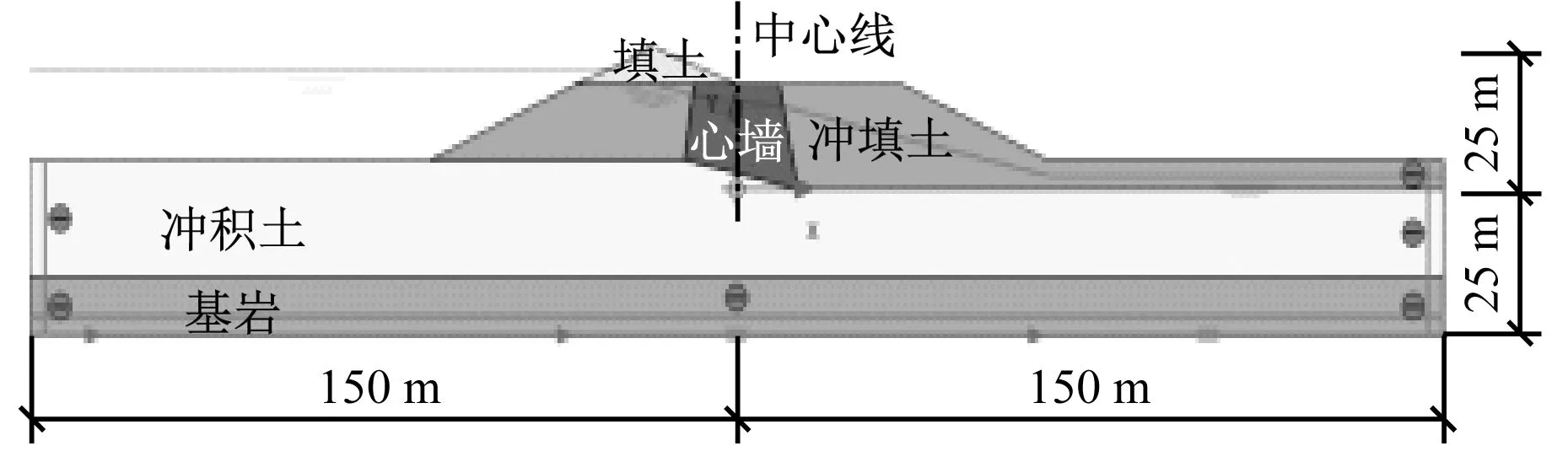
图2 San Fernando大坝数值模型尺寸

大坝各处表面位移的数值计算结果与实际结果对比如图3所示。由图3可见,数值模拟结果与实际测量结果数值相差不大,二者规律基本吻合。这说明UBC本构模型能较好模拟出砂土液化的现象,能对砂土地基液化中的结构物变形进行分析。

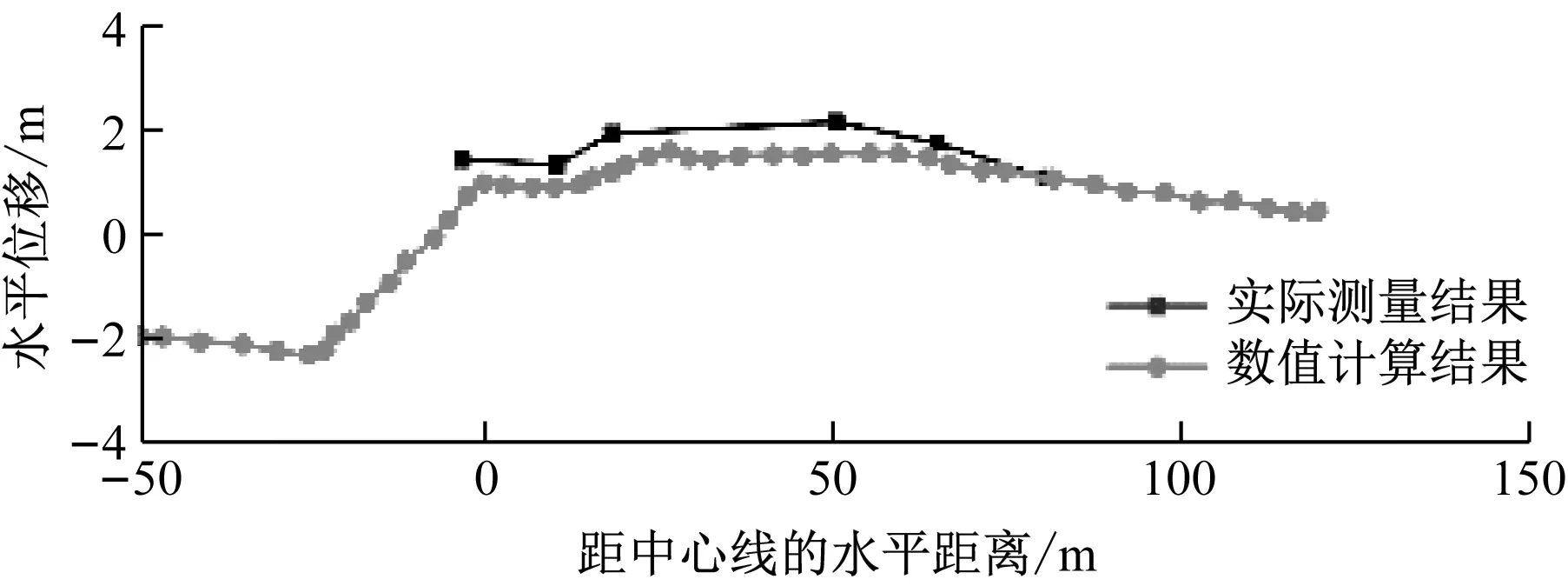
a) 水平位移

3 崇明线工程的建模与计算

3.1 模型建立

崇明线工程的数值模型尺寸如图4所示。模型长度为75 m,深度为35 m,隧道直径为6.9 m,模型全局水位线设置在地表处,隧道和砂质粉土地基之间使用默认的接触面来模拟隧道-土之间的相互作用。

图4 崇明线工程数值模型尺寸

建模时,Plaxis2D软件使用15节点三角形平面应变单元自动来创建网格。网格的生成主要考虑土层、结构物、外部荷载及边界条件。为了平衡结果精度和计算时间,需要划分合适的网格尺寸。由文献[13]可知,若要准确模拟动力荷载的传播过程,就需限制网格的平均尺寸。文献[13]建议,平均单元尺寸Δ应小于等于输入波最高频率分量相关波长λ的1/8,即:

(1)

式中:

vs,min——最低剪切波速;

fmax——输入波最高频率。

3.2 计算结果分析

3.2.1 排水措施的加固动力响应

为对比排水措施效果,本文对比分析了隧道不采取排水加固措施及隧道两侧采用排水桩加固(仅考虑其排水性能)两种工况下的模型动力响应。

Plaxis2D软件会根据应力点的超孔压比来判断该点是否液化。图5为崇明线工程可液化层的液化点图。由图5可知:不采用排水措施工况下,隧道四周土体液化现象明显;在隧道两侧采用排水措施的工况下,仅在上部隧道存在较为密集的液化点,排水体周围几乎不发生液化现象。这可以说明采用排水措施有效限制了动力荷载作用下可液化层液化现象的发生。

a) 不采用排水措施工况

在隧道两侧采用排水桩加固的工况下,可液化土层内不同深度位置(P1、P2、P3、P4)处的超孔压比时程曲线如图6所示。P1、P2、P3、P4距隧道的水平距离为12 m,埋深分别为28、18、12、6 m。可以看出:采用排水加固措施后,可液化土层内仅在浅层发生了较大的超孔压累积,而隧道深度附近可液化层内的孔压比上升较慢。

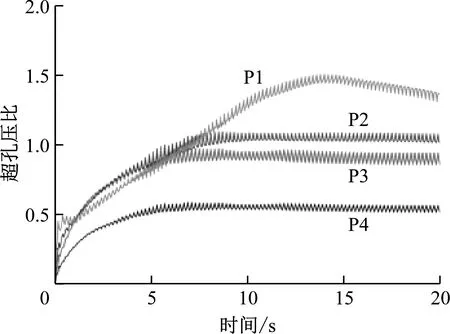
图6 采用排水桩措施工况超孔压比时程曲线

在隧道同一深度的可液化地层中,选择距一侧排水桩的不同距离s(s取2、4、6、8 m)设置观测点,最终得到不同s处的超孔压时程曲线,如图7所示。

图7 不同s处的超孔压比时程曲线

由图7可见:随着s的增大,超孔压比的峰值开始逐渐增大,分别对应0.40、0.55、0.90和1.00;当s=6 m时,超孔压无明显消散过程;s=2 m和s=4 m处的超孔压比峰值较小,而s=6 m和s=8 m处的超孔压比峰值明显增大。这说明排水措施具有抗液化作用,且在s≤4 m范围内的作用效果明显。

3.2.2 不同动力荷载强度下的动力响应

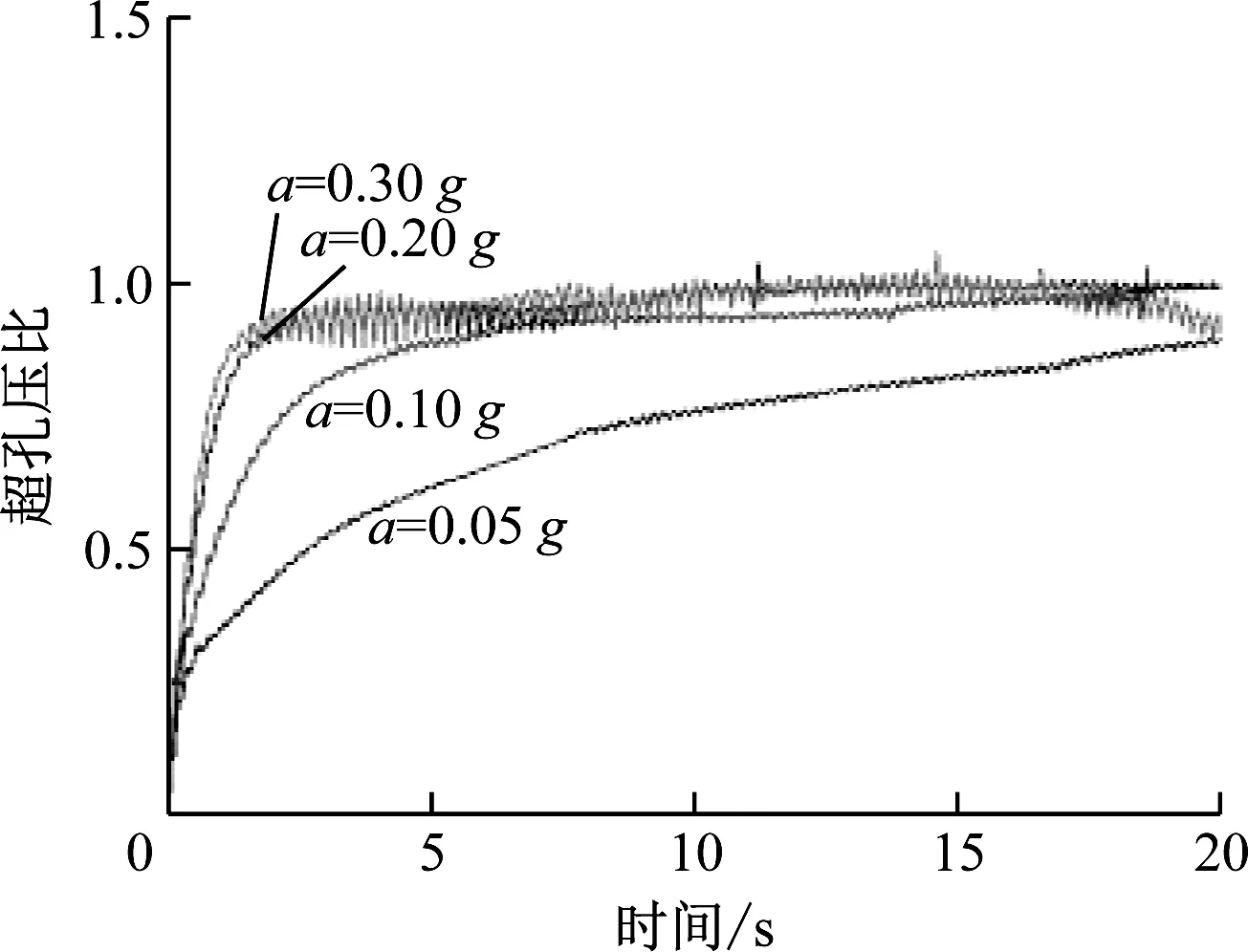
为分析不同强度动力荷载下的可液化地基动力响应,本文设计了加速度峰值不同的4种动力荷载,其加速度峰值a分别为0.05g、0.10g、0.20g和0.30g。本文对典型的P1、P2及P4处超孔压比进行分析,得到不同a下不同深度处的超孔压比时程曲线如图8所示。

a) P1处

由图8可见:a= 0.05g时,可液化土层在各深度处超孔压比于20 s左右达到峰值;a=0.10g时,在7 s左右超孔压比达到峰值;a= 0.20g及a= 0.30g时,在2.5 s左右超孔压比达到峰值;不同动力荷载强度下的超孔压比峰值基本相同,其中上部土层中超孔压比峰值达到1.24,中部土层中超孔压比峰值达到1.22,下部土层中超孔压比峰值达到0.93。说明不同动力荷载强度条件主要对超孔压积累和增长模式产生有影响,随着a的增大,超孔压累积的速率越快,超孔压比达到峰值的时间就越短。

a为0.05g、0.10g和0.20g工况之间的超孔压累积速率差异明显:a=0.20g和a=0.30g整体差异较小;a超过0.20g后,可液化层超孔压比积累增长规律基本一致。这表明:动力荷载强度低于某一阈值时,动力荷载强度就不足以使得可液化土层的超孔压达到峰值,但随着动荷载强度的增大,可液化土层超孔压比达到峰值的时间越短;而动力荷载强度达到某一阈值后,可液化土层超孔压比累积增长规律基本一致。

4 结论

1) 利用Plaxis2D岩土工程有限元分析软件,建立UBC3D-PLM本构模型,可有效模拟可液化地层中的孔压动力响应。

2) 隧道两侧采用排水桩加固措施,能有效限制动力荷载作用下可液化土层发生液化现象,且在排水设施一定范围内的防液化作用效果显著。

3) 动力荷载强度对超孔压积累和增长模式有较大影响。当a达到0.20g后,可液化土层超孔压比累积增长规律基本一致,均在2.5 s时达到完全液化状态,并且超孔压比随着振动荷载作用时间的增加而趋于稳定。