破解多元等式条件下的最值问题

安徽省阜南县第一中学 (236399) 李金龙

用基本不等式解决某些含有多元等式条件的最大值或最小值问题是一种常见手段,但有些题目的结构复杂,条件隐晦,会出现相对比较难的题目,需要有扎实的基本功和一定的解题技巧,那么这些能力的来源是接受规范的解题方法指导和有一定量的典型题目的训练,本文从介绍常用解题方法的角度,以题例说方法,希望给读者朋友有一点启发．

一、配凑等式

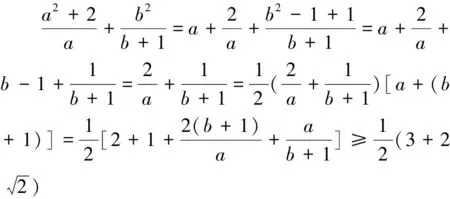
点评：由于待求结论式中的分母是a和b+1,所以必须由条件a+b=1进行配置得a+(b+1)=2,通过审题,及时利用好已知条件是迅速解题的重要措施．

二、适时配方

例2 已知实数x,y满足x2+y2-xy=1,求x+y的最大值．

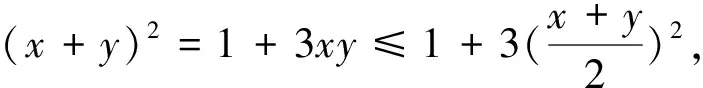
点评：本题从探求的结论出发,运用配方手段构造了一个关于x+y的不等式,然后再解不等式完成了解题．

三、先行放缩

点评：本题利用给出的条件先得到一个不等式,然后再对这个不等式变形,这样有方向地、有目的地对结论式进行放缩处理,从而化解了问题难点．

四、及时化简

点评：观察给出的条件式或结论式,如果需要进行化简处理的必须先行解决,常规的化简手段,包括消去复杂的分式、根式等,本题中利用基本不等式化去根号非常重要.

五、适当变形

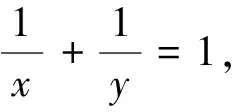
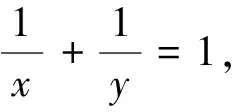
点评：通过先把给出的条件进行变形,然后再将待求结论进行有目的的变形转化,构造出适合运用基本不等式求解的基本模型,从而达到了解题目的.

六、连续放缩

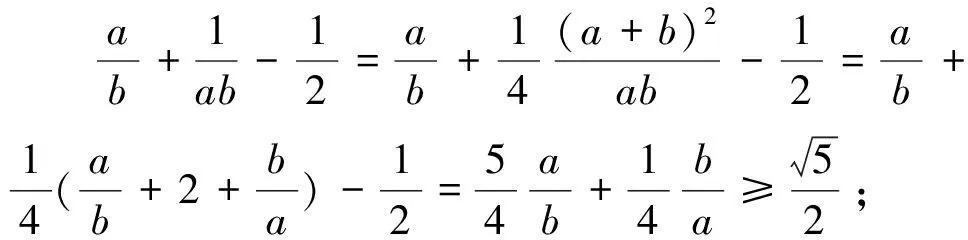
点评：在解题中两次运用了基本不等式进行了放缩处理,是解决结论式情况比较复杂问题的有力手段,应该注意的是,连续放缩时取等号的条件必须保持一致．

七、整体构造

例7 若实数a,b且a>1,满足条件ab-4a-b+1=0,求(a+1)·(b+2)的最小值．

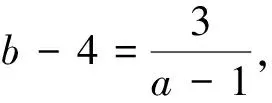
点评：由于题设中没有直接告诉相关的因式,通过全面考查所给的条件和待求结论,然后瞄准结论式对条件式进行重新整理,然后进行整体消元,构造出只含一个参数的关系式,并且可运用均值不等式进行求解最值处理,这样就明确了变形方向,化解了问题的难点．

八、三角替换

点评：若在题设中含有两个正项和为1(或某个特定的数值),就可以选用三角换元,如此就能够利用三角函数的有界性求得最值问题,从而达到解题目的．

九、分母换元

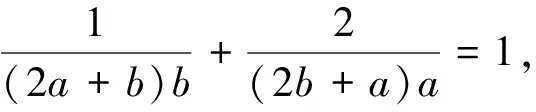
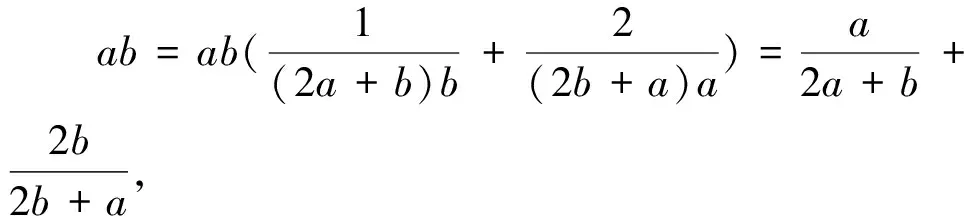
点评：通过审题发现,条件式中的分母结构比较复杂,所以对分母进行换元势在必行,而换元后出现了可使用基本不等式解题的规范模型,明确了解题方向．

十、因式换元

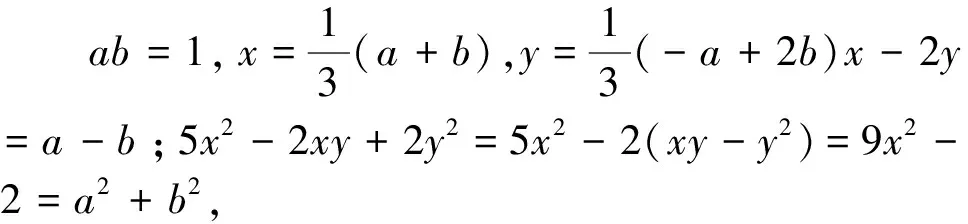
点评：在对已知条件式因式分解后,然后对其中的两个因式分别换元,这样降低了次数,再用新变量替换原来的变量,从而揭示了隐含关系,表明了后续解题方向.