建立学生解题的整体观——以“关键点法”解决三角函数图象问题为例

浙江省杭州市余杭高级中学(临平中学) (311103) 庞海燕

一、引言

现实世界存在着大量的“周而复始”的现象,三角函数是刻画周期现象的重要工具.以全国Ⅰ卷为例,三角内容一般设置2-3个考点,主要是“三角恒等变换”、“三角函数的图象和性质”、“解三角形”,题型设置基本固定,分值在15-22分之间(如下表).

20-22年全国Ⅰ卷对三角内容考查

具体到三角函数象及性质而言,从基础知识的理解和应用,到运算能力,再到数形结合、转化与化归的思想方法都有涉及,高考试题的考查总体稳定,形式新颖,有一定难度.在教学中,如何让学生通过教师的解题示范教学,理解和掌握数学概念、定理和方法,逐步经历知识的激活、检索、提取与组织,使解题与数学思维发展并行,并且能够上升数学思想层面呢?

整体观引领下的数学解题教学不仅有利于教师重组教学内容,促近学生联结相对分散的事实、知识、技能或经验,整体理解学习内容、思想方法,促进情感态度等方面发生转变,而且使学生的学习变得更高效、更有深度和延展度,促进学科核心素养的发展.

“关键点法”是笔者在教学过程中摸索出的解决三角函数图象问题的一种方法,“关键点”可以是具有特殊函数值的点,也可以是给定区间的端点.抓牢“关键点”可以根据图象求解析式、图象平移、求解参数范围,从而串联起多种题型,实现多题一法,丰富学生解题经验,培育解题智慧,从而建立学生解题的整体观.

二、识图定式

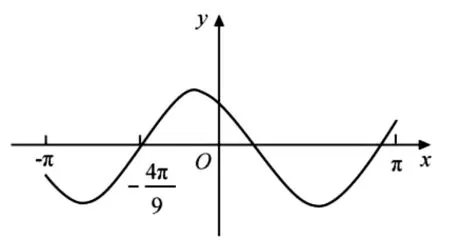
图1

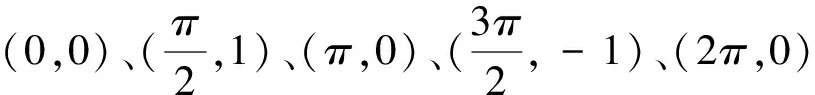
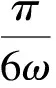
三、图像平移

肉羊生产中通常还存在生产性能低与繁殖率低的问题，多数绵羊会受到季节性发情期的影响，一年最多只能完成一产，限制肉羊生产环节中利润的获取空间，直接影响肉羊养殖的经济效益。因此，可以进一步采用两年三产高频繁殖技术，通过人工授精、冷冻精液等多种模式实现集中配种、集中生产，极大提升公羊资源的利用率，节省养殖成本和风险。另外，在营养、繁殖季节以及激素诱导等方面进行必要的调控，实现羊羔的早期断奶，母羊尽早发情配种，提升繁殖指数，有效缩短肉羊的饲养周期，带来良好的经济效益[3]。

方法提炼：将前后两个函数的解析式化为同名同正负同w后,抓牢前后两个解析式中ωx+φ=0的x,它们就是“关键点”,它们的移动情况是整个图象移动情况的反映.举例如下:

四、确定参数

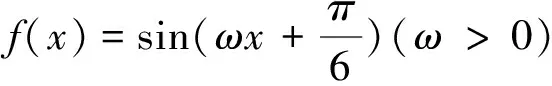
方法提炼：给定单调区间,首先利用区间长度不超过半个周期,可求出ω的大致范围,再根据自变量x的取值范围,得到ωx+φ的取值区间,根据ω的范围求出区间端点的范围,在正弦或余弦函数的图象找到满足条件的区间,得到不等式组,从而求解.

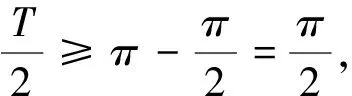
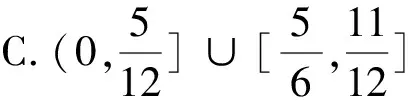
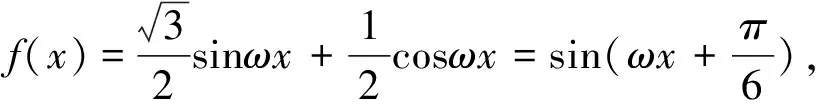
五、教学反思

笔者在教学实践中发现,利用“关键点法”能够串联起原本独立的题目,学生不仅提高了解题能力,也对三角函数图象问题有一个更整体的认知.实际上,在解题教学中,对于数学方法,教师要深切挖掘领会该种方法的数学内涵、数学原理,使之上升到数学思维层面;对于数学思维,则又结合相关类型的数学问题,通过分析其思维共性,使之上升到数学思想的层面;对于数学思想,则通过开放课程系统,如结合友邻学科的知识、学生的生活阅历、社会生产活动等等,使之继续上升到哲学层面.最后再用理性、辩证的方法指导解题活动,通过这种循序渐进方式,使各个阶段的教学行为之间形成紧密的关联,切实培养学生的解题的整体观,促进核心素养落地.