关于一道向量试题的变式探究
2023-08-26 03:43:14广东省佛山市顺德区容山中学528303马崇元
中学数学研究(江西) 2023年9期
广东省佛山市顺德区容山中学 (528303) 马崇元
平面向量兼具代数与几何的信息,所以在求解时可分别从数与形的角度思考.因为向量的抽象性,学生在面对向量问题时常常无法发现解题的突破口.特别是当向量与其他知识相融合时,该现象更加明显.笔者以一道向量模拟试题为例,研究其解题过程,分析其命制方式,并据此构造出多个变式供读者参考.
一、题目及分析
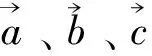

二、解法呈现
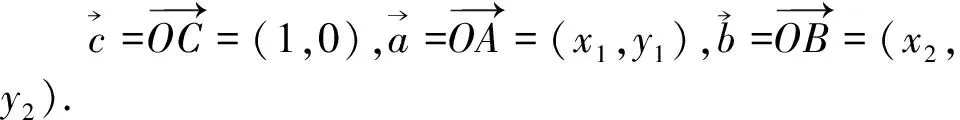
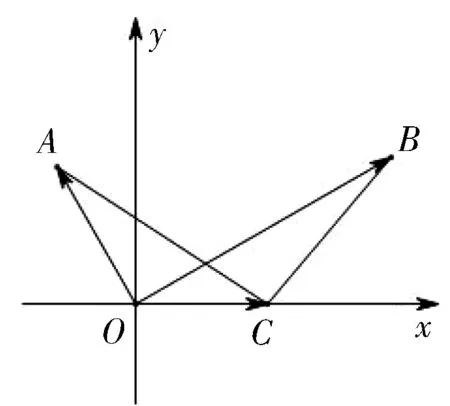
图1
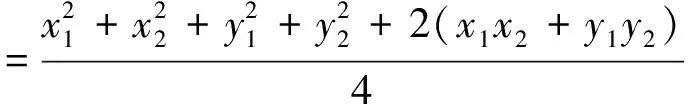
反思:该解法的核心突破口在于研究了点M的轨迹,如何想到研究该点的轨迹则显得较为突兀.为了自然的联想到该结论,其本质在于对三角形中线公式的理解.
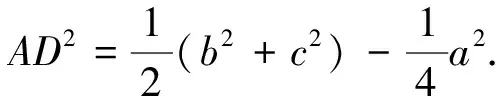
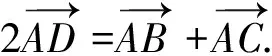
现利用该结论研究原问题,可得如下的解法:
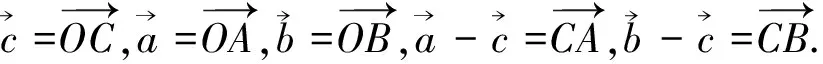

图2
三、变式探究
原问题最终都转换为以圆为背景的最值问题,我们可从这一方向,设计出如下的变式供大家练习.

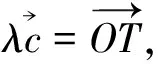
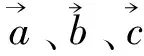

答案:上述两个变式的答案同变式1.


在上述解答中,原问题在于探究AB中点E的轨迹,我们还可考虑通过构造AB的三等点来设计变式.在构造之前,我们先研究一下三等分线的相关公式.

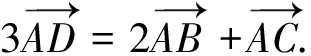
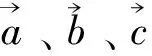

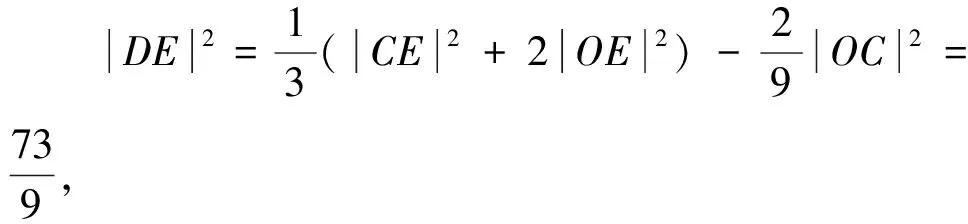
类比上文中变式1-变式4的构造方法,也可将变式5进行相应的改编.在变式5中,笔者构造了三等分点的命题方式,我们也可命制出其他等分点对应的试题.
猜你喜欢
中学生数理化·七年级数学人教版(2020年12期)2021-01-18 06:57:42
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
读友·少年文学(清雅版)(2020年4期)2020-08-24 07:36:26
读友·少年文学(清雅版)(2020年3期)2020-07-24 08:57:04
现代装饰(2018年5期)2018-05-26 09:09:39
高中生·天天向上(2018年2期)2018-04-14 09:33:14
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:51
中国三峡(2017年2期)2017-06-09 08:15:29
求学·理科版(2016年11期)2016-11-29 19:34:24
试题与研究·中考化学(2016年1期)2016-09-30 18:44:09

