再谈圆锥曲线焦点弦长的统一公式
厦门大学附属实验中学 (363123) 林秋林
一、问题的提出
例1 已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,求|AB|+|DE|的最小值.
该例题是普通高中教科书《数学选择性必修第一册》(湖南教育出版社,2019年第1版)课本P149习题3.3的第12题,原题则出自2017年高考全国数学理科I卷.原题作为选择题,有不少资料上都利用了抛物线焦点弦的弦长公式来给出简解,过程如下:
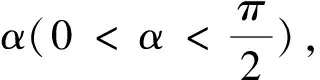
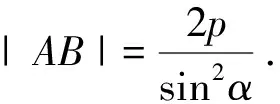
上述解析利用公式逻辑清晰,目标明确,过程简洁有效.在学生掌握了这个二级结论的前提下,作为选择题的解法无可厚非.只是例1作为解答题,这个直接利用二级结论的解答过程就明显不够严谨了.笔者曾在高三某个班级利用该题做了一个小测验,结果发现该班不少优秀的同学光知道利用二级结论进行所谓“秒杀”,规范的解答过程反而不知道怎么书写了,不是缺步就是跳步,这不禁让笔者忧心不已.高三复习该不该任由学生去记忆类似的二级结论呢?二级结论是否会影响学生对数学的学习?笔者不禁陷入了思索与困惑.
二、问题的思考
《普通高中数学课程标准(2017年版2020年修订)》针对平面解析几何内容,对学生提出了具体的学业要求.即能够掌握平面解析几何解决问题的基本过程;根据具体问题情境的特点,建立平面直角坐标系;根据几何问题和图形的特点,用代数语言把几何问题转化为代数问题;根据对几何问题(图形)的分析,探索解决问题的思路;运用代数方法得到结论;给出代数结论合理的几何解释,解决几何问题.同时对高考命题原则,《课标》明确指出:考查内容应围绕数学内容主线,聚焦学生对重要数学概念、定理、方法、思想的理解和应用,强调基础性、综合性;注重数学本质、通性通法,淡化解题技巧;融入数学文化.由此可见,强调利用二级结论来解题,会让学生陷入强化解题技巧的误区,也会使学生忽视数学的本质,甚至会因此而对数学兴趣索然.那二级结论是不是都没有积极作用?教师是不是要制止学生去钻研、理解二级结论呢?为此,笔者专门和一些成绩优秀的同学做了交流,其中有几个学生反映以前在考试时经常会因方法的选择不当、本身计算能力的不足等原因,导致成绩一直不够理想,而在掌握并能熟练使用一些二级结论后,对数学解题(特别是选择题或填空题)有了较大的信心,不仅提高了解题速度,而且解题的准确率也有一定的提升,成绩自然也更加突出.
有一个学生还以例1为例,告诉笔者:如果知道抛物线的焦点弦长公式,虽然不能直接利用,但是知道了弦长可以和直线与对称轴的夹角建立联系,这可以为解题指引了方向,并且还能检验自己得到的结论是否准确.该生同时向笔者展示了如下解法:
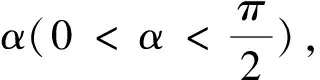
三、问题的进一步探讨
看到上述解法,笔者很是欣喜.与学生的这些交流心得,也犹如给笔者吃了颗定心丸.因此笔者试着在另一个班级利用例1与学生们一起探讨了圆锥曲线焦点弦长的统一公式及使用方法,而后笔者利用例2又做了一次测验.

这次的测验结果相当喜人,笔者发现有更多的同学给出了以下解析.
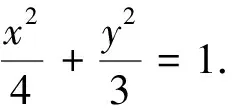

该解法相比较常规解法,省略了讨论的步骤,同时最后的弦长和转化为关于α的函数,也能较简便地得到取值范围.笔者现场提问了其中一位给出上述解法的同学,他的解释是:本题中虽然不能直接利用圆锥曲线焦点弦长的统一公式,但是既然知道焦点弦长可以看作关于直线倾斜角的函数,就想到了设直线的参数方程,从而得到上述解法.

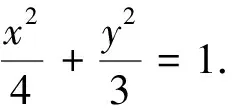



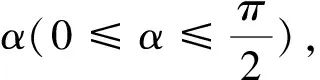
四、结语
以上通过对圆锥曲线的焦点弦长的统一公式的教学,举一反三,给沉闷的数学教学注入了一丝活力,提升了学生的学习兴趣,调动了学生的积极性,从而提高了课堂教学效率和教学质量,同时也发展了学生的逻辑推理、数学运算等核心素养.著名数学教育家波利亚曾说过:“解题可以是人的最富有特征性的活动,假如你想要从解题中得到最大的收获,你就应该在所做的题目当中去找出它的特征,那些特征在你以后求解其他问题时,能起到指导的作用.”笔者认为,二级结论其实就是所谓的“特征”,是对一些重要的数学概念、定理、性质等进行的深入总结,它可以有意识的引导学生从结论中发现解题思路,从证明中完善解题过程.要达到这样的正面效果就要求教师要指导学生知其然更要知其所以然.数学题目是永远做不完的,如果学生能适当掌握一些二级结论,就能解决更多相应的问题,这确实会大大提升学习效率.当然这里教师也要对二级结论进行筛选,指导学生去粗取精,避免学生陷入泥潭.

