施工阶段曲线预应力连续刚构桥空间受力分析*

王 伟,朱利明,钱思沁,易晨阳

(1.北京城建中南土木工程集团有限公司,北京 100012; 2.南京工业大学交通运输工程学院,江苏 南京 210009)

0 引言

在我国交通建设和城市化发展进程中,曲线梁桥逐渐成为一种重要桥梁类型[1-2],并在轨道交通中得到较广泛应用。在城市轨道交通建设中,曲线桥可很好地连接各方向交通,且能满足交通功能需要及缓解地形地貌限制,在一定程度上增加其经济效益。虽然曲线桥具有独特优势,但其因曲率影响不仅会产生弯矩,还会产生极大扭矩,因此,受力更复杂[3];当曲线桥受到扭转和竖向弯曲时,其箱梁截面会发生约束扭转和截面畸变,使腹板及截面应力分布极不均匀,其截面空间受力效应也更显著[4]。目前,国内外学者对曲线桥空间受力开展大量研究。Agarwal等[5]采用有限元方法研究了斜交和曲率对单室钢筋混凝土斜弯箱梁桥主梁最大弯矩、剪力、扭矩和垂直挠度的影响,并与直线桥进行比较。冯升阳等[6]对同跨径下曲线箱梁桥与直线箱梁桥在一期恒荷载作用下各控制截面弯矩、剪力和应力差异进行分析。认为现行普遍使用的基于梁系理论的有限元法计算结果不能真实反映曲线箱梁空间受力分布。Gupta等[7]通过三维分析模型研究曲率和偏斜对结构的影响,得出偏斜度和曲率对结构产生绝对最大纵向力矩的临界位置及力矩临界截面位置有显著影响。Wang等[8]以某三跨连续宽曲线箱梁为工程背景,通过模型荷载试验得到宽曲线连续箱梁应力和挠度分布,提出采用均匀系数表示曲线桥不均匀力。张晔芝等[9]依托某五跨连续预应力曲线刚构桥,研究曲线刚构桥变形和受力状态及空间效应的相关规律。研究表明,最大悬臂状态下截面内、外侧竖向位移及应力有较大差别。

在自重和预应力作用下,曲线连续刚构桥因弯扭耦合作用,悬臂施工时曲线内、外侧产生应力差。当半径过小时,其弯扭耦合效应明显,即截面内、外侧应力差值不可忽略。因此,研究在最大悬臂状态时半径对箱形截面梁内、外侧应力值的影响分析。并且引入以直代曲正应力修正系数,提出一种能用于计算曲线连续刚构桥正应力的实用计算方法。

1 工程背景及有限元模型

1.1 工程背景

宁句线五跨连续刚构桥为南京至句容城际轨道交通工程东郊小镇—古泉(侯家塘)区间所设的 1座变截面曲线预应力连续刚构桥,跨径布置为45m+3×80m+45m,桥梁位于圆曲线半径为800m的平面上。

该结构主梁采用单箱双室直腹板箱梁截面,梁顶宽9.95～12m,梁底宽6.45～8.5m,按二次抛物线变化;中支点截面梁高5m,跨中和边支点截面梁高2.5m。该桥箱梁顶板厚度均为30cm。悬臂浇筑段底板厚度在跨中截面为30cm,支点截面处为75cm,按二次抛物线形式变化。本桥采用双薄壁实体墩,薄壁墩间距2m,墩高分别为21,27,24,17m。主墩、主梁均采用C50混凝土。纵向预应力钢绞线采用符合国际标准的1 860MPa级φs15.24高强度低松弛钢绞线,预应力管道采用增强型金属波纹管成孔,真空压浆。腹板预应力束张拉控制应力均为 1 302MPa, 顶板预应力束张拉控制应力为1 209MPa。 顶板预应力束、腹板预应力束布置分别如图1,2所示。

图1 顶板预应力束平面布置

图2 腹板预应力束立面布置

1.2 有限元模型

采用有限元软件ABAQUS建立空间实体有限元模型,对全桥进行各施工阶段、预应力、自重作用下的分析计算。采用ABAQUS有限元软件分别对混凝土结构及预应力钢筋进行建模。混凝土采用三维应力几何线形的 C3D8单元,预应力钢束采用桁架线性几何单元,单元类型T3D2。采用Embedded region方法实现钢筋与混凝土间的耦合[10],并运用降温法模拟预应力张拉力施加。

为验证ABAQUS有限元模型的正确性,建立相同条件下MIDAS Civil有限元模型。在最大悬臂状态下,2种模型主梁各截面顶板应力计算结果对比如图3所示。

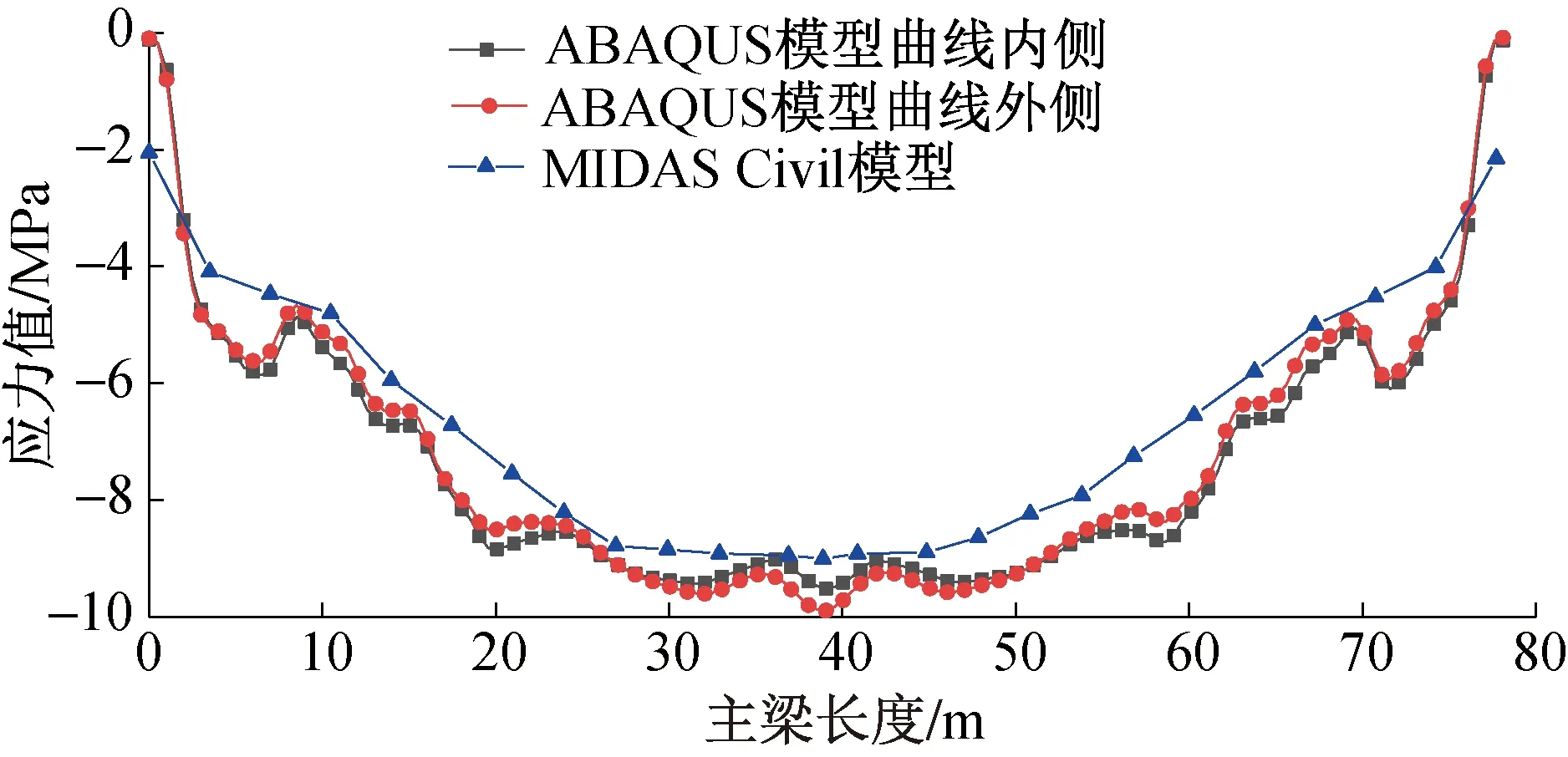
图3 最大悬臂状态不同模型顶板正应力对比

由图3可知,在自重和预应力共同作用下,ABAQUS模型中曲线连续刚构桥顶板应力最大值为-9.896MPa, MIDAS Civil模型中顶板应力最大值为-9.01MPa。 ABAQUS实体模型主梁顶板应力与MIDAS Civil梁单元模型计算所得的应力较接近,且在变化趋势上基本一致。距悬臂根部6m处小里程侧主梁顶板实测内、外侧应力值分别为-9.283,-9.516MPa, 计算内、外侧应力值分别为-9.316,-9.533MPa, 误差分别为-0.354%,0.178%,实测数据与计算数据吻合较好。以上均验证了该有限元模型适应于宁句线五跨连续刚构桥,计算结果具有一定准确性

由于曲线连续刚构桥弯扭耦合效应的作用,在ABAQUS模型中曲线连续刚构桥横截面上的应力存在一定差异,利用MIDAS Civil在计算曲线连续刚构桥时计算结果不够精确,无法较好地反映横截面应力变化。综上,有必要采用ABAQUS实体有限元模型研究曲线连续刚构桥空间受力。

2 曲线连续刚构桥正应力空间分布

以依托工程配筋为参照,在跨径布置、施工方法、预应力钢筋数量、横截面布置和张拉应力相同的情况下,改变桥梁曲线半径参数。桥面中心线对应弧长为78m,以弧长对应圆心角为整数选取曲线半径,为更好地看出曲线半径对施工结构受力的影响,曲线半径取值如表1所示。

表1 曲线连续刚构桥不同曲线半径取值

以图4所示的特征截面为代表,特征截面沿纵向依次编号为1～7。在自重和预应力作用下,最大悬臂状态下半径150m的曲线连续刚构桥应力如图5,6所示,其余半径特征截面云图类似。

图4 控制截面划分

图5 半径150m曲线连续刚构2—2截面正应力云图(单位:MPa)

图6 半径150m曲线连续刚构4—4截面正应力云图(单位:MPa)

2—2,4—4截面外顶板正应力随曲线半径变化规律分布分别如图7,8所示。由图7,8可知,对于弧长为78m的最大悬臂状态曲线连续刚构桥来说,当半径由R=150m减小至R=50m时,除墩顶截面附近处,其余各控制截面外侧应力值随着半径减小而逐渐减小,内侧应力值则随着半径减小而逐渐增大;而在墩顶截面位置处截面外侧应力值随着半径减小而增大,内侧应力值随着半径减小而减小。

图7 不同半径下2—2截面处顶板正应力

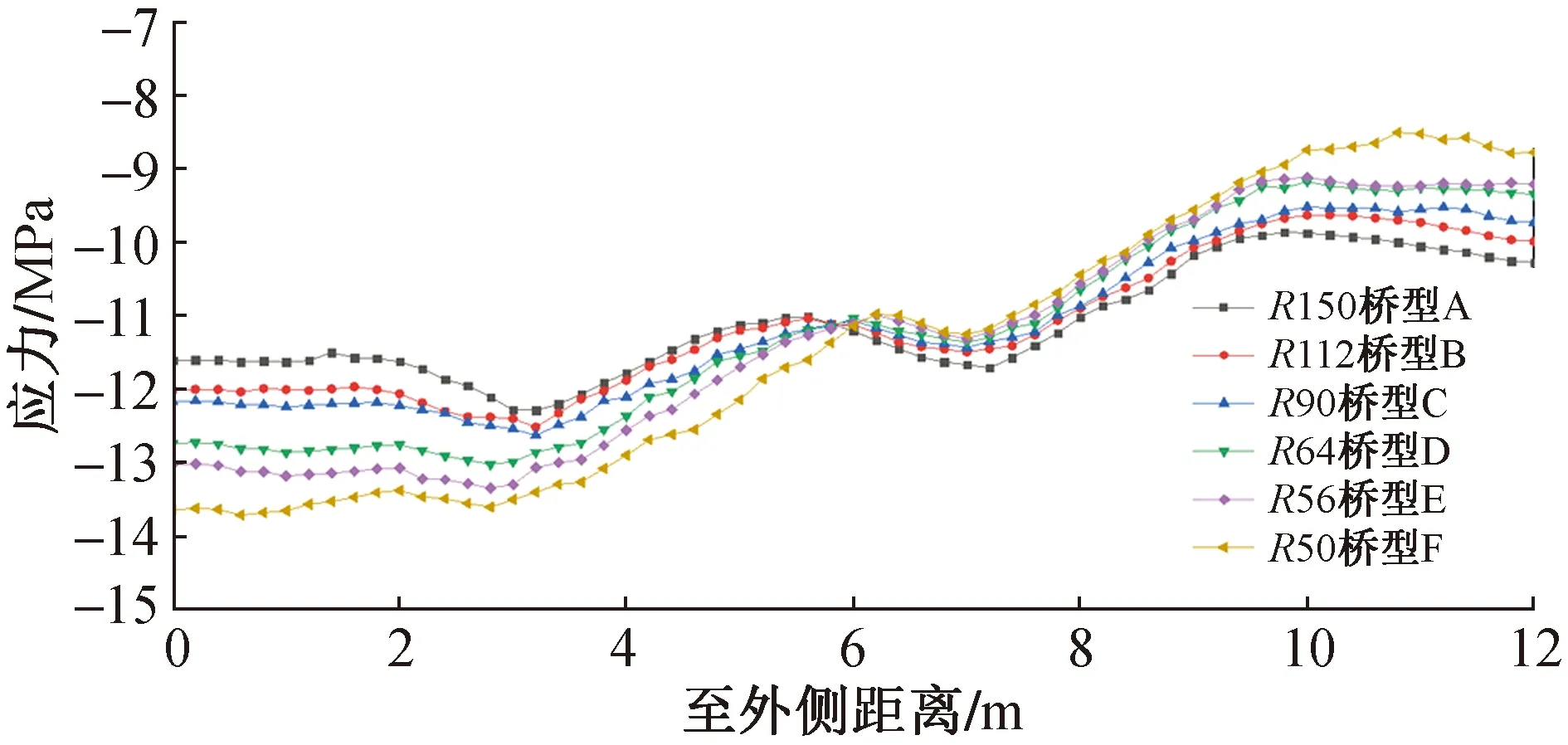
图8 不同半径下4—4截面处顶板正应力

为进一步分析,提取各控制截面曲线内、外侧正应力值,计算分析结果如表2所示。

表2 曲线半径对控制截面正应力影响规律

由表2可知,在最大悬臂状态下,T构顶板大部分区域产生压应力。与直线桥相比,除墩顶截面附近外,其他各控制截面顶板内侧压应力大于外侧压应力,并且曲线半径越小,其内、外侧应力差异越大;而在墩顶附近截面位置处呈现出内侧压应力小于外侧压应力,且随着半径减小其内、外侧应力差值越大。这可能是因为曲线箱梁桥外侧竖向变形大于内侧变形,但限于墩顶截面竖向约束,致使墩顶截面外侧弯曲正应力大于内侧。曲线悬臂刚构桥由于弯扭耦合效应的影响,即使在对称荷载作用下,结构在横截面上的应力分布仍不均匀。随着曲线半径减小,结构各截面应力分布不均匀程度将逐渐增大,这也是由于曲线连续刚构桥随着曲线半径减小,其弯扭耦合效应相应增大。

3 以直代曲实用计算方法研究

3.1 实用计算方法研究

曲线梁桥由于弯扭耦合效应的存在使曲线连续刚构桥受力状态比直线连续刚构桥更加复杂,并且曲线连续刚构桥半径越小,弯扭耦合效应更明显,内、外侧应力差值也变得越大。

术后认知功能障碍指术前无精神、神经系统性异常，围手术期受多种因素影响，术后发生理解能力、抽象思维、定向力障碍，以及记忆受损，且合并社会活动功能降低等现象。术后认知功能障碍是社交能力、认知能力、人格发生改变的中枢神经性并发症[4]。术后认知功能障碍的发病机理尚不明确。研究表明，引发术后认知功能障碍的危险因素包括受教育程度、遗传、疾病史、麻醉药物、年龄、手术类型、智力水平等。较为确定的一点是高龄为引发术后认知功能障碍的影响因素之一[5]。

对于一般直线梁桥来说,通常无需考虑结构扭转。但对于曲线梁桥,在其结构分析中,扭转分析和计算占重要地位。因此,要着重研究不同半径下控制截面扭转效应产生应力的影响。借助对这一主要因素的研究,得出扭转变形导致的正应力值与半径的关系。

文献[11]将弯曲桥跨中弯矩与相同跨径直线桥跨中弯矩之比称为弯曲桥跨中弯矩修正系数。鉴于此,引入截面正应力修正系数表示曲线梁桥扭转变形产生的内、外侧正应力值与相同跨径直线梁桥内、外侧正应力值之比。通过修正系数对直线梁桥正应力值进行修正,从而得到曲线梁桥对应的正应力近似值,这样在设计时可采用直线梁桥或折线来代替弯曲,达到简化计算的目的。不同半径曲线连续刚构桥正应力修正系数如表3所示。

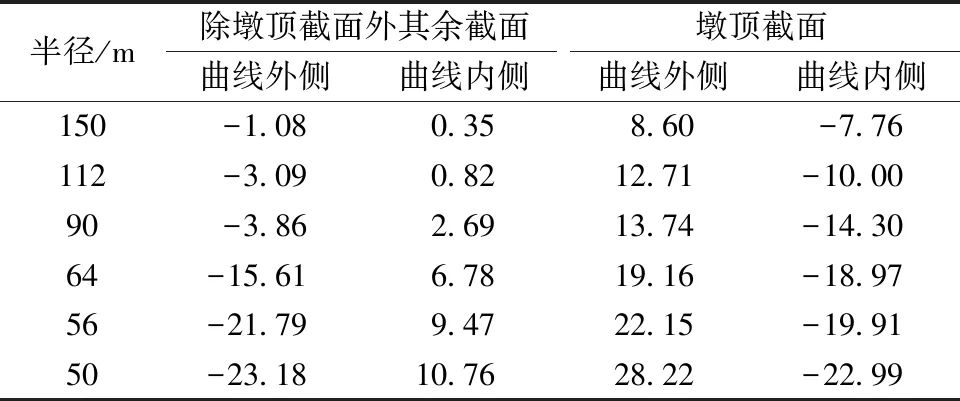
表3 截面内-外侧正应力修正系数

选择不同半径曲线连续刚构桥控制截面正应力放大系数制作半径-修正系数折线图,并由此拟合应力修正系数与半径关系曲线,如图9,10所示。

图9 不同半径下除墩顶外其余截面正应力修正系数

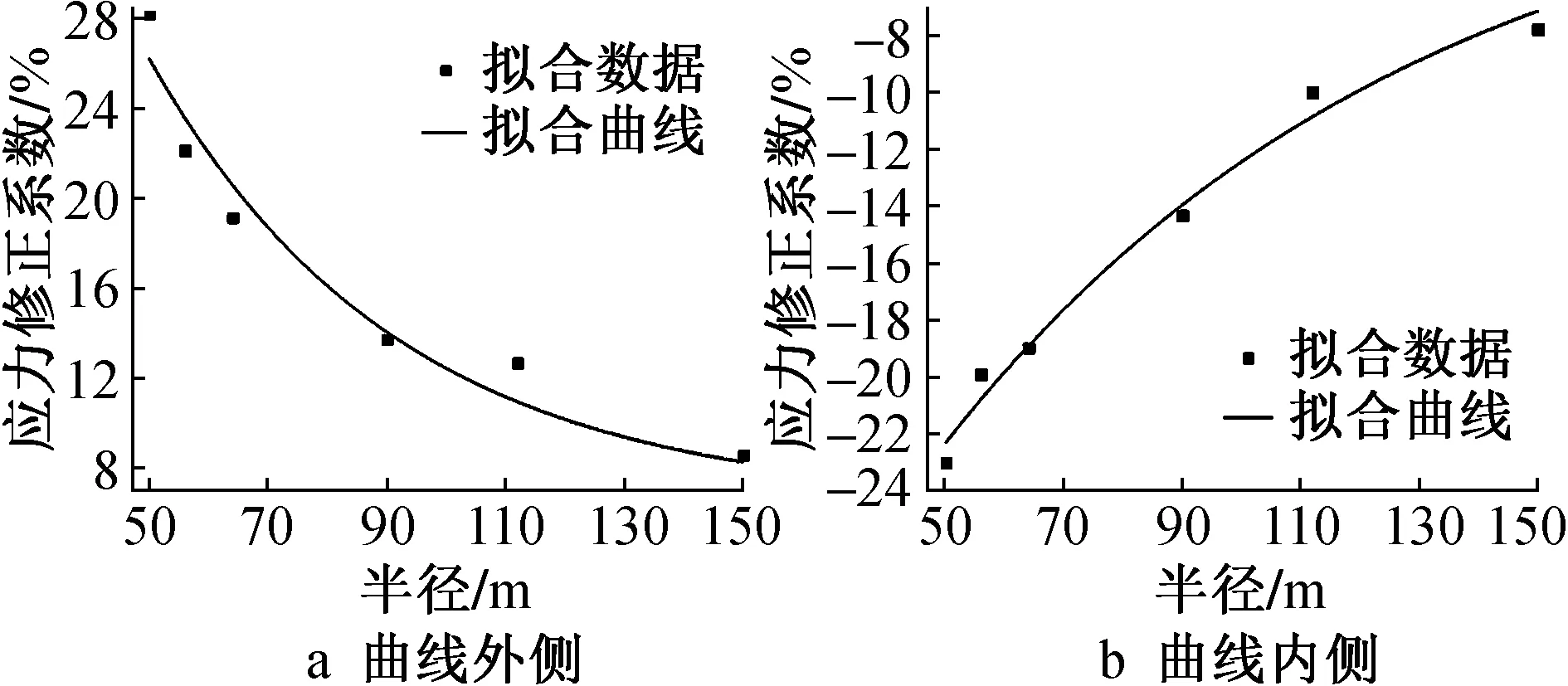
图10 不同半径下墩顶截面正应力修正系数

由图9,10可知,使用指数曲线可以很好地拟合出截面正应力修正系数与半径关系曲线。当曲线连续刚构半径不断增大,修正系数变化速度逐渐减小,拟合曲线也趋于平缓;而当曲线连续刚构半径不断减小时,修正系数变化速度逐渐变大。其应力修正系数与曲线半径的关系表达式如下。

1)除墩顶外其余截面曲线外侧修正系数为:

(1)

2)除墩顶外其余截面曲线内侧修正系数为:

(2)

3)墩顶截面曲线外侧修正系数为:

(3)

4)墩顶截面曲线内侧修正系数为:

(4)

式中:y为应力修正系数(%);R为半径(m)。

按式(1)～(4)计算出修正系数后,在自重和预应力作用下,曲线梁桥应力可按式(5)计算:

曲线梁桥正应力=直线梁桥正应力×

(1+正应力修正系数)

(5)

可见,通过引入正应力修正系数可在一定程度上基于直线梁桥计算结果,对曲线桥在自重和预应力荷载作用下的正应力值进行近似计算,实现以直代曲近似计算,方便工程应用。

3.2 实用计算方法应用效果

为验证以直代曲实用计算方法应用效果,依托工程CY58号墩施工至最大悬臂状态,桥面中心线对应弧长为78m,以弧长对应圆心角为60°选取曲线半径为74.48m,建立相应模型。根据实用计算方法,求出不同截面正应力修正系数如表4所示。

表4 不同截面正应力修正系数

通过以直代曲实用计算方法,利用截面正应力修正系数进行直线梁桥应力值修正计算,近似得出半径为74.48m曲线连续刚构桥内、外侧应力值。并将上述结果与曲线梁桥有限元模型内、外侧应力值进行比较分析。在以直代曲实用计算运用过程中,由于墩顶附近截面与其他截面之间修正系数变化较大,其墩顶附近截面与周围截面应力值存在突变。因此,将0号块端部截面应力值与墩顶截面正应力值之间采用平滑曲线连接,如图11所示。

图11 实用计算方法应用效果

由图11可知,当桥面中心线对应弧长为78m、曲线半径为74.48m时,曲线连续刚构桥内、外侧应力值与直线梁桥应力值相差较大。采用以直代曲实用计算方法对直线梁桥正应力值进行修正,得到的结果与该曲线连续刚构桥模型计算结果较接近。这也证明了该实用计算方法效果较好,为类似曲线连续刚构桥的以直代曲简化计算提供思路。在曲线连续刚构桥初步设计阶段,可以极大地简化计算并提高工作效率。

4 结语

本文分析了最大悬臂状态下曲线连续刚构桥内力和变形分布规律。在最大悬臂状态下,通过改变模型中的几何参数(即半径),分析半径对主梁内、外侧应力的影响,并通过引入修正系数,提出曲线梁桥正应力实用计算方法。结论如下。

1)在最大悬臂状态下,墩顶附近截面曲线外侧应力大于曲线内侧应力,除墩顶附近外其余截面曲线内侧应力大于曲线外侧应力。随着曲线连续刚构半径的减小,墩顶附近截面曲线外侧应力逐渐增大,曲线内侧应力逐渐减小;而除墩顶附近截面外其余截面随着半径减小,曲线外侧应力逐渐减小,曲线内侧应力逐渐增大。且从数据来看,随着半径减小,全桥范围内曲线内、外侧应力差值增大。

2)当半径较小时,曲线连续刚构桥弯扭耦合效应明显,导致曲线内、外侧应力差值较大,在设计时必须给予重视,不能按直线梁桥计算。对于不同半径曲线连续刚构桥来说,提出以直代曲正应力修正系数的具体表达式。并在此基础上给出一种计算正应力值的以直代曲实用计算方法。在曲线连续刚构桥初步设计阶段,极大地简化了计算,提高其工作效率。