基于机器学习的力场模型研究综述

陈美霖，刘端阳，徐黎明，汪洋

1.中国科学院计算机网络信息中心，北京 100083

2.中国科学院大学，北京 100049

3.中国科学院半导体研究所，北京 100083

引 言

由于材料领域的飞速发展，现如今已经积累了大量的数据以及无数相关的问题有待解决[1]。相比传统方法研究材料动力学性质，急需一种高效快速的方法来解决这一难题。近年来，机器学习(Machine Learning, ML)在各个领域都发挥了重要的作用，因此，用机器学习的方法来解决现有的问题不失为一种不错的选择。

在研究材料动力学性质的方法中，分子动力学使用较为广泛，它是以量子力学、经典力学、统计力学为基础，通过牛顿力学来模拟分子系统的运动状态，并利用计算机数值求解运动方程的方法。传统的分子动力学计算速度快，能一定程度上反映材料的稳定性，热力学性质等多种性质，但由于其使用的是较为简单的经验力场，计算精度有限；而从头算分子动力学(Ab initio molecular dynamics, AIMD)将分子动力学与密度泛函理论(Density Functional Theory, DFT)相结合，将系统中的粒子划分成原子和电子，原子的质量大且运动速度较慢，可以用经典力学来处理，而电子的质量小且运动速度较快，可以用密度泛函理论来处理。该方法的提出可以很好地解决分子动力学无法对化学键的断裂描述的问题[2]。

AIMD 由于考虑了电子相互作用的细节，并且使用量子力学方法对全体原子进行了统一考虑，因此计算精度大大提高，但也因此计算代价高昂，往往只能应用于数十个到数百个原子的小体系，且模拟时长最多到纳秒级[3-4]。对于体系较大的系统，一般采用传统经验力场来建模，传统的科学方法使用一些近似值求解，分析计算，并用更高水平的计算或实验的参考数据验证所获得的结果。但是当所研究的系统过于复杂，仅靠现有知识无法建立可靠的模型时，这种方法并不是十分有效。并且力场往往在牺牲计算效率的条件下才能获得较高的计算精度。

然而，一个精确力场的搭建十分耗时，并且需要大量的专业知识和技术。而机器学习方法可以有效解决传统方法无法解决的复杂问题[5]，在一定程度上可以有效地平衡计算效率和计算精度之间的制约关系，并将AIMD 方法的计算精度和经典力场的计算效率融合，使应用于研究更大的分子系统体系成为可能[6]。

机器学习力场(Machine Learning Force Fields,MLFF)[7-11]是通过一些机器学习算法，采用生成的结构特征作为输入来进行参数拟合。它通过从数据中的结构或者模式中学习输入和输出之间的功能关系，而不依赖于先入为主的固有化学键的概念或关于相互作用的知识[12]，从数据中学习训练[6]。该方法的提出可以有效地缩小与传统力场方法的计算精度差距，同时可以提高计算效率，减少人工干预。在理想状况下，经过训练的模型可以反映出量子力学潜在的有效规则。因此, 使用AIMD 的结果数据作为训练集，使用机器学习力场方法训练得到的力场，有望在接近AIMD 的精度情况下获得接近甚至超过传统力场的计算效率[13-14]。目前，实现机器学习力场模型的较多，如深度神经网络[15]等，深度神经网络训练时通常需要大量的数据，在自然科学中收集这样的数据集往往是不可能的，因为每个训练点都是计算成本高昂的从头算或其他实验测量得来的。因此，机器学习力场模型的数据效率成为一个关键因素。这也是机器学习力场模型建立的初衷，即将基本物理定律或知识直接实现到机器学习模型的体系结构中。与传统机器学习方法相比，当使用有限的参考数据集时，此类模型可以表现出优越的性能。此外，基于知识的机器学习力场模型可以深入了解复杂的原子间相互作用[16-17]。本文将在第1 节对材料机器学习的基础理论知识进行简单的讲解；并在第2 节对使用较为广泛的机器学习力场模型进行介绍，探索方法的可行性和有效性；最后在第3 节进行总结和分析。

1 理论基础

在半导体领域，一般用薛定谔方程(Schrödinger Equation, SE)来描述原子核和电子的相互作用。但SE 只能对极其简单的体系进行求解，如氢原子等。在求解复杂的体系时，随着系统复杂度的增加，计算成本也随之飞快增加，与此同时，无法很好地平衡计算成本和计算精度之间的关系。因此，用SE 来求解复杂体系存在较大困难。玻恩–奥本海默近似(Born-Oppenheimer approximation, BO 近似)的提出可以很好地改善这个现象，BO 近似将电子的运动和原子核的运动分开，因原子核质量比电子质量大几个量级，可几乎认定为是静止的，从而可以忽略掉原子核的运动。因此，可将体系简化为电子的薛定谔方程来求解，即电子的能量取决于核外的电势，而电势又由电子的位置和核电荷数决定。通过将原子核和电子的库仑斥力相加，即可得到系统的总势能[6]。

在BO 近似下，系统的能量是原子核位置的函数，即一个分子几何结构映射出一个体系能量值，不同原子位置的能量一起构成了势能面(Potential Energy Surface, PES)。一个封闭的系统需要满足能量守恒定律。在分子体系中，能量由动能和势能构成。因此，力一定是势能相对于原子位置的负梯度。这样可以保证当原子运动时，原子们总是能够获得与损失的势能相同的动能[6]。

虽然BO 近似在一定程度上简化了SE 方程的求解，但近似下的计算仍具有较大的困难。因此，想要得出分子动力学模拟的每个时间步下的能量和力仍是比较困难的[19]。而力场的提出可以在一定程度上避开方程求解的问题。从而将问题的难点从方程求解转换到寻找合适的力场以及力场参数化上来。而机器学习方法可以将这种困难通过从数据中学习自动化实现，将先验知识融合到更为复杂的模型的构建中[20]，从而简化了力场的构建过程。本文将在1.1 与1.2 节概述机器学习中两种方法，基于内核的方法以及神经网络(Neural Network, NN)方法。

1.1 基于内核的方法

核函数方法起源于非线性支持向量机模型(Support Vector Mmachines, SVM)。在核方法中，内核是核心，它将原始空间中的向量作为输入向量，返回特征空间中向量的点积函数，即将输入空间映射到高维特征空间。新的特征空间具备更强的表达能力以及在原始特征空间中的非线性拟合效果[1]，它将原始空间中的非线性拟合转换为新特征空间中的线性拟合。使用核函数，不需要显式地将数据嵌入到空间中来，这样可以有效地简化复杂的计算。但核函数对于较大的数据集并不十分受用，因为无法存储整个核矩阵，因此可能需要重新计算核函数。基于内核的方法不需要知道特征空间以及转换函数，同时使在高维特征空间中以低计算成本获取线性关系成为可能。

可以看出，机器学习模型的性能高低与核函数的选取息息相关。因此，选择一个合适的核函数对于机器学习方法具有十分重要的意义。

1.2 神经网络

神经网络是通过模拟生物神经元相互传递信号的方式，由许多相互连接的处理单元组成的非线性自适应信息处理系统[21]，旨在对神经元形成的复杂网络建模[6]，从而达到学习经验的目的。在数据选择上，神经网络通常需要较多的训练数据才能达到较为理想的计算精度，但同时，它们也可以更好地应用于较大的数据集中。神经网络可以通过对输入数据进行高维特征映射，转换成特征描述符(descriptor,desc)，从而通过特征描述符作为输入来进行参数的拟合[22]，学习构建出力场[19]。

在神经网络中，输入层和输出层的节点数量比较容易确定。输入层的神经元数量等于数据中输入变量的数量，输出层神经元的数量与每个输入关联的输出的数量相同。往往困难之处在于确定合适的隐藏层数量以及其节点数量。隐藏层的层数不同，网络模型实现的功能也并不相同。

神经网络至少具备一个隐藏层，可以对非线性的复杂模型系统进行建模，多出来的隐藏层可以为模型提供更高的抽象水平，从而提高模型的能力。当数据流经网络时，输入层的第i个神经元将输入数据乘以权重Wij，并将其输出到下一层的第j个神经元。神经元之间的权重反映了网络的连接强度，神经网络可以通过调整权重来提高整个模型的性能[23]。因此，神经网络具有较强的表达能力，只要有足够的深度和宽度，神经网络可以以任何精度来逼近所有函数。图1 是一个多层神经网络的结构图。

2 机器学习力场模型

目前，用于构建机器学习力场的模型非常多，如GAP[7]、DPMD[10]、HDNN[9]、PhysNet[8]、ANI[24-26]等。在分子动力学模拟中，机器学习力场模型可以分为以能量为中心和以力为中心的模型[27]。以能量为中心的模型通过学习势能面，并计算势能面的导数得到力[28]。如梯度域机器学习(Gradient-Domain Machine Learning, GDML)[28]、对称梯度域机器学习(Symmetrized Gradient-Domain Machine Learning,sGDML)[29]通过学习能量和力之间的梯度函数来简化能量和力的表达形式。另外一种以能量为中心的模型如DimeNet[30]、DimeNet++[31]、SchNet[32]采用图神经网络的方法，实现对能量的平滑预测[33]。

物质运动具有能量，一般用场来描述物体的运动状态。而力场用来估计分子内原子之间以及分子之间的力。力场是原子间势，可以使用能量来描述场。因为力实际上可以认为是能量的负梯度。

其中，Fi表示作用在每个原子上的力；E为体系内的能量；ri表示原子i的笛卡尔坐标向量。

力是矢量，在空间中的每个原子位置需要用笛卡尔坐标系来描述，而能量是标量，对空间中的每个点只需要用一个值来描述。因此与使用力来描述场比起来，用能量来描述力场更为简单。

力场建立了原子坐标和系统相应总能量之间的映射[34]。传统力场是基于晶体结构键长和键角来拟合参数的。与经典力场相比，机器学习力场可以不利用先入为主的理论知识，不对经验函数进行参数化表示，而是通过现有数据来学习原子的能量及其他特征，作为其函数表示，来代替经典力场[19]。该系统中的能量为系统中所有原子能量的总和。

其中，E为体系内总能量；R为原子位置。从上述方程也可以看出作用在原子上的力与距离较远的原子的种类和位置并没有很强的相关性。因此，机器学习力场模型可以依托系统内总能量来推测特征与原子能量之间的关系[35]。

另外一种是在以力为中心的模型，在该模型中，力是通过网络模型来直接预测的，然后与实际的力进行比较。同时，加入了残差连接，改善随着网络深度的增加而带来的梯度消失、梯度爆炸等问题[24]。使用力为中心的模型可以有效减少在以能量为中心的模型中计算力所需的额外花销，从而提高计算效率[36]。

因为能量是标量，而力为有3 个方向的矢量，所以目前以能量为中心开发的机器学习力场模型居多，而通过以力为中心的模型来计算能量，需要考虑到各个方向上的力的作用，具有一定的复杂性。

本文将在2.1 至2.3 小节介绍几种机器学习力场中比较常见的模型方法，如sGDML、 SchNet、Force-Net 等，方便读者对MLFF 有一个较为清晰的认识。

2.1 sGDML

GDML[37]采用核方法构建了一个可以节约能源的力场，可以减少能耗、增加效率和降低成本，避免因噪声放大导致导数需要应用于参数化势能模型中的问题[1]。该模型通过将物理定理与数据自驱动方式的机器学习技术相结合，可以实现对复杂的多维势能面的构建。sGDML 模型作为GDML 的对称变体，在GDML 模型的基础上加入了所有相关的物理对称性[29]，因此可以更为精准地对力场进行从头算分子动力学模拟[12]。

许多物理系统对于某种变换是不变的，这种不变性一般称为对称性。分子系统的物理对称性大致分为时间对称性、空间对称性以及对给定分子的特定的动态和静态对称性。时间对称性一般指的是能量守恒定律。封闭系统中的能量既不会凭空产生，当然也不会凭空消失，它只会从一种形式转换成另外一种形式，而总能量始终保持不变。原子是运动的，运动过程中会将损失掉的势能转化为动能，以保持总能量不变，在时间上表现为封闭系统的能量守恒。空间对称性包括能量的旋转不变性和平移不变性。空间的旋转不变性直观上来讲就是空间没有特殊的方向，可以说该空间是各向同性的。如果将分子系统沿空间某方向平移任意位移后，它的物理规律完全相同，那么该系统具有空间上的平移不变性。这些对称性在GDML 模型中已经充分体现[28]。另外，分子具有刚性空间群对称性，也就是物理上的反射现象；同时还具有动态的非刚性对称性，如甲基的旋转等[3]。由于考虑了这些对称性[38]，可以通过用分子的对称变换来扩充数据集，以便训练出性能更优的模型，对原子的能量和力进行准确预测。该模型相较于GDML 模型的优势与系统中的对称性数量有直接关系，对于对称性较高的系统而言，sGDML模型的性能提升较大，而没有对称性的体系，其在性能提升上并无变化。

sGDML 已在MD17、MD22、CCSD 等公开数据集上广泛应用并表现出良好的性能。表1 将通过GDML 和sGDML 两种方法在MD17 数据集的表现对比，分析其在1,000 个训练样本上对力和能量的预测能力，其中力的测试误差以kcal mol–1(Å–1)为单位，能量的测试误差以kcal mol–1为单位。由表可知，sGDML 在苯、乙醇等具有对称性的分子上，其预测性能有显著提高，但在尿嘧啶等非对称性分子上，sGDML 相较于GDML 的性能并没有提升[3,28]。

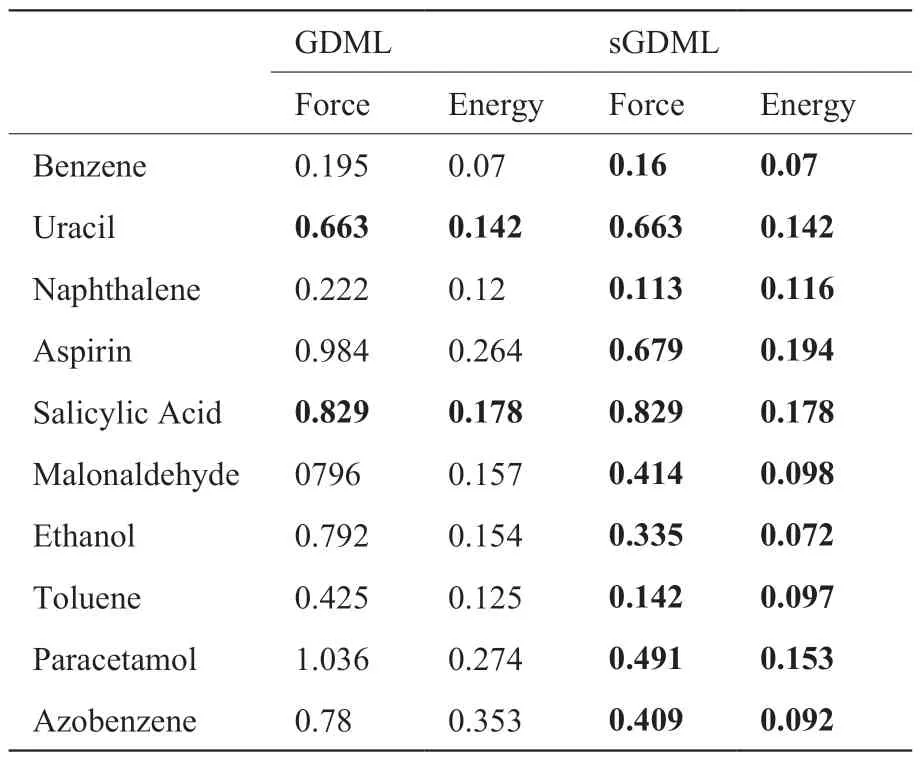
表1 GDML 和sGDML 的预测性能Table 1 Comparison of GDML and sGDML

sGDML 模型在分子动力学模拟中已经展现出较强的优势，其全局性虽然可以提高预测精度，但这一特征也限制了它的可转移性。对于一个分子体系的模型不能用来推测另外一个不同分子体系的能量和力[29]。因此，sGDML 模型的适用性以及扩展到更大的分子体系方面的能力仍有待提高。

2.2 SchNet

机器学习模型中比较常见的一个子类就是原子神经网络，该模型具有不同的体系结构，但大致可以分为两类：基于描述符的模型[39]，将原子的属性作为输入；以及直接从原子类型和位置学习表示的端到端的结构[40]。

SchNet 是一种基于连续滤波器卷积的端到端的深度神经网络结构[41]，旨在对原子系统进行建模，学习分子能量与原子力预测的表示，反映了基本的物理规律，如原子指标和平移不变性以及关于原子位置的平滑能量预测和能量守恒等。SchNet 作为深度神经网络，具有多层网络结构，当原子表示通过网络时，这些网络层会对它们进行转化，同时处理在上一层合并的高维原子信息[42]。SchNet 通过对每个原子更新以及每个原子能量的池化过程，最后得到对力的预测结果。由于SchNet 实现了旋转不变的能量预测，因此预测得到的力在结构上是旋转等变的[39]。为了确保旋转不变性，SchNet 的连续滤波器只使用了原子距离作为输入特征，而在消息传递过程中丢失了角度信息。因此，原子类型的变化可能会导致原子之间的相互作用力有明显差异[24]。

SchNet 已在QM9、MD17、ANI1 等公开数据集广泛应用。表2 展示了SchNet 在MD17 数据集的表现，并与sGDML 作比较，本数据选取1,000 个训练样本并对力和能量训练并预测，其中力的测试误差以kcal mol-1 (Å-1)为单位，能量的测试误差以kcal mol-1 为单位。由表可知，SchNet 可以表现出较好的性能，但大体上略逊色于sGDML[3,42]。

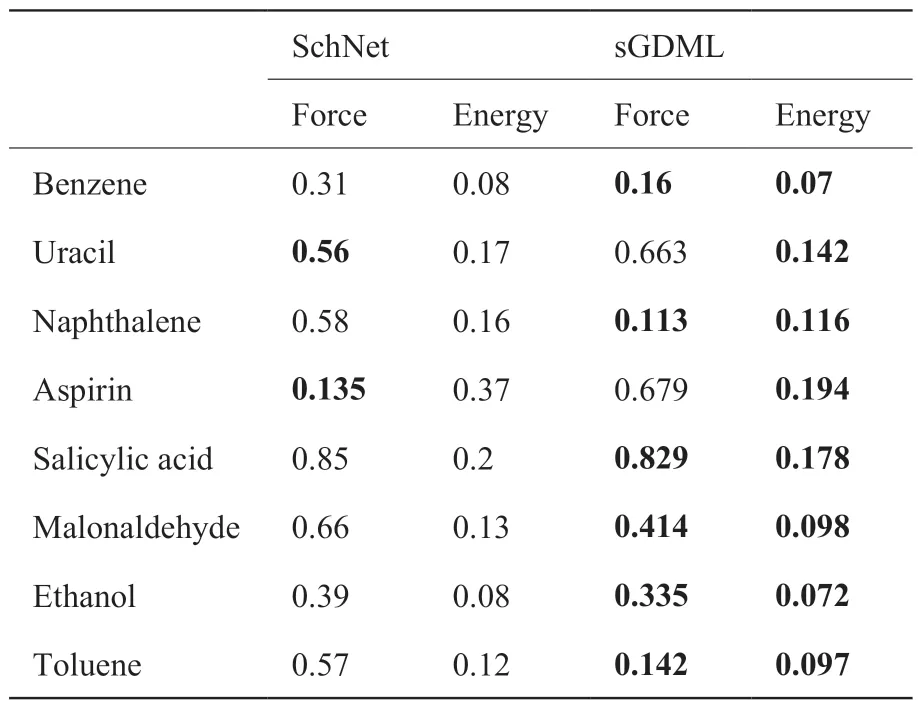
表2 SchNet 和sGDML 的预测性能Table 2 Comparison of SchNet and sGDML

SchNet 可扩展性较强，具备高效计算的能力，但只使用原子距离以确保对能量预测的旋转不变性，无法很好地捕捉到3D 结构，泛化性能有待提高。

2.3 ForceNet

ForceNet 是一个以力为中心的模型，它遵循基于图网络的模拟器(Graph Network-based Simulators,GNS)框架，通过使用物理意义上的大规模增强数据集来预测力[36]。ForceNet 没有在模型体系中施加显式的物理约束，可以捕捉到完整的3D 原子位置。因此，ForceNet 预测的力是平移不变的，但不具备旋转不变性[24]。ForceNet 的输入是原子的结构，即一组原子的3D 空间位置，输出是每个原子的3D 矢量，用来表示预测的(x,y,z)3 个方向上的力。ForceNet将原子表示为图神经网络(Graph Neural Networks,GNN)[43]中的节点，将原子之间的相互作用表现为GNN 中的边，节点输入特征包括原子序数以及其他重要属性[44]。该模型使用较为基础的函数以及非线性激活函数Swish 来进行消息传递，从相邻节点传递的消息迭代更新节点。ForceNet 遵循GNS 框架的编码器-解码器架构，编码器使用迭代消息传递来获取每个原子周围的3D 结构；解码器使用多层感知器(Multilayer Perceptron, MLP)直接预测每个原子的力，它能有效地捕捉到非线性的复杂3D 原子间的相互作用[24]。目前，FoceNet 已应用于OC20 数据集[24]。ForceNet 在训练以及预测过程速度都比较快，同时也可以实现对力的精准预测，但其以力为中心对力场建模的复杂性仍有待完善。

3 总结与展望

本文重点关注机器学习在构建力场中的应用，介绍了机器学习力场的发展背景以及重大进展，讲述了几种机器学习力场中比较常见的模型方法，如基于核函数的sGDML 模型，以及基于神经网络的SchNet 模型和ForceNet 模型，方便读者对该领域有一个清楚的认识。就目前数据而言，sGDML 加入了相关的物理对称性的考量，表现出更加优异的性能。与传统力场方法相比，机器学习方法的引入很大程度上降低了时间消耗和昂贵的成本。随着半导体领域数据量的增多，要解决的问题也接踵而来，随着机器学习力场这一跨学科领域的蓬勃发展，它在该领域将会起着重要的作用。机器学习力场可以简化力场生成过程，减少人工干预，逐步代替经典力场来实现高水平的分子动力学模拟。

从机器学习力场在分子动力学模拟中的应用[45]已经可以看出其发展不可限量，不仅如此，MLFF 在生物领域[46]、材料领域[47-50]、化学领域[51]同样有着广泛的应用，但其仍存在着许多问题等着人们去挑战。如：

（1）对于比较复杂的分子动力学模拟系统，简单的特征描述符无法很好地展现其性能，因此MLFF会对原子特征描述符的构建有着更高的要求；

（2）目前MLFF 的主要应用对象仍不是特别大的分子体系；对于特大分子体系，MLFF 由于计算成本、精度等限制并未展现出较好的性能；

（3）通过MLFF 生成的针对某一种分子体系的力场并不适用于另外的一种不同分子的体系，其通用性有待提高。

机器学习力场是一个新兴的领域，仍有很多未知的可能等待人们去探索。因此，本文认为未来可以从以下几个方面进行优化：

（1）通过降低复杂势能面的维度或者通过增强物理先验知识来降低计算复杂度，使MLFF 应用在特大分子体系成为可能，提高MLFF 在特大分子体系上的性能；

（2）优化模型性能，在保证精度的前提下，尽可能降低计算成本，将机器学习力场模型与更复杂的模型系统结合，并对其实现精准预测；

（3）提高模型的可扩展性和泛化性，增加先验知识的干预，改善特定MLFF 模型只对某特定领域最优的现象，将机器学习力场扩展到更广泛的领域。

总之，机器学习力场是一个有深远研究意义的领域，仍有很多未知的方法和应用，并且对于理论、算法以及实践的改进空间都比较大。鉴于MLFF 这一跨学科领域的成功，相信MLFF 在未来一定会成为众多领域的重要组成部分。

利益冲突说明

所有作者声明不存在利益冲突关系。