自适应樽海鞘群算法求解考虑运输时间的柔性作业车间调度

牛昊一，吴维敏，章庭棋，沈微，张涛

(1.浙江大学 工业控制技术国家重点实验室，浙江 杭州 310027；2.浙江大学 智能系统与控制研究所，浙江 杭州 310027)

柔性生产能够实现对生产资源的广泛协调与有效利用，已成为智能制造的发展趋势.在柔性生产中，柔性作业车间调度问题（flexible job shop scheduling problem，FJSP）被证明是具有NP-hard特征的组合优化问题[1]，引起了国内外学者的广泛关注.自动导引车（automated guided vehicle, AGV）是高效的移动式物料搬运机器人，已被应用于各类智能制造系统中[2].由于AGV在搬运过程中存在运输时间，研究考虑运输时间的柔性作业车间调度问题不仅能够有效提高制造过程的灵活性和稳定性，而且更具有学术价值和工程意义.

目前，国内外对考虑运输时间的柔性作业车间调度问题已开展了部分研究.Zeng等[3]提出两阶段启发式算法，为作业工序安排最合适的运输设备.Zheng 等[4]基于禁忌搜索算法，提出新型的混合整数线性最优化模型，解决加工机器和AGV的协同调度问题.Mousavi等[5-6]通过融合元启发式算法，提出新型的多目标调度算法求解该类问题.此外，多Agent调度策略[7]、改进粒子群算法[8]、混合遗传算法[9]和聚类多智能体模型[10]等优化算法也被相继提出，但没有一种通用方法能够计算得到所有FJSP问题的精确最优解，发展高效且鲁棒的求解算法成为FJSP研究领域的一个重要方向.

樽海鞘群算法（salp swarm algorithm, SSA）是由Mirjalili等[11]提出的新型智能群体算法，具有控制参数少、计算量小且求解性能优秀的特点，已被成功应用于如目标分类问题[12]和无源时差定位问题[13]领域.该算法在生产调度领域的研究尚不多见，现有成果仅有针对普通柔性作业车间调度的研究[14].基础樽海鞘群算法存在迭代后期容易陷入局部最优、搜索精度下降、求解结果不稳定等问题.为此，许多学者针对基础樽海鞘群算法作出相应的改进，采用混沌映射[15]、融合时变惯性权重因子[16]和虚拟种群[17]等方式提高SSA算法在搜索最优解时的性能，但在应用于柔性作业车间调度问题时仍有进一步改进的空间.

针对考虑运输时间的柔性作业车间调度问题，本文提出自适应樽海鞘群算法（adaptive salp swarm algorithm，ASSA）.通过基于随机密钥的3层编码方式实现离散调度解的连续编码，设计惯性权重策略和自适应更新领导者-跟随者数量策略，使得领导者更好地引导跟随者进行搜索，引入禁忌搜索策略增强算法的局部搜索能力.通过基准算例进行仿真测试，验证所提算法的性能，采用边际效应理论研究AGV数量对完工时间的影响.

1 问题描述与数学模型

1.1 问题描述

考虑运输时间的柔性作业车间调度问题可以描述如下.有N个工件在M台机器上加工，每个工件至少有一道加工工序，每道工序至少有一台可选择的加工机器.有S辆AGV负责搬运工件，每个工件在完成当前工序后由AGV运输到下一台机器进行后续工序的加工.AGV在机器间搬运工件时存在一定的运输时间.每个工件由作业车间的物料传送装置，即装载站台，传送进作业车间，再由AGV按照工序将工件运输至加工机器.除此之外，本文遵循以下假设.

1）柔性作业车间内的生产设备由装载站台和加工机器组成.

2）各加工机器的缓存区容量无限.

3）零时刻所有待加工工件和AGV的起始位置都在装载站台.

4）同一个工件的相邻工序在同一台机器上进行加工，不需要AGV进行运输.

5）AGV在完成运输任务后停靠在当前加工机器站台，等待被安排下一个运输任务.

6）不考虑AGV在运输过程中产生的死锁和碰撞.

7）生产过程具有稳定性，不考虑加工机器故障、工件疲劳和恶化等效应.

1.2 数学模型

以最小化最大完工时间为优化目标，建立数学模型.目标函数及相关约束的描述如下.

式中：Cmax为所有工件的最大完工时间；i表示工件编号，取值为i= 1, 2, 3,···,N，其中N为待加工的工件总数；Ci为工件i的完工时间.

约束条件为

式中：j表示工序编号，对于工件i，取值为j=1,2,3,···,OPi，其中OPi表示加工工件i需要的工序数量；EPij为结束加工工件i的第j道工序的时刻.

式中：s表示AGV编号，取值为s=1, 2, 3, ···,S；SPij为开始加工工件i的第j道工序的时刻；ETs为AGVs运输工件的结束时间；yijs为决策变量，当工件i的第j道工序由AGVs运输时为1，否则为0；为工件i的第j道工序所选择机器上一道工序的结束加工时间.

式中：m为机器编号，取值为m=1,2,3,···,M；Pijm为工件i的第j道工序在机器m上的加工时间；xijm为决策变量，当工件i的第j道工序在机器m上加工时为1，否则为0.

式中：STs为AGVs运输工件的开始时间；u为机器编号，取值为u=1,2,3,···,M；tmu为工件在机器m和机器u之间的运输时间；zsm为决策变量，当AGVs空闲时所在位置为机器m时为1，否则为0；

式中：wij为工件i的第j道工序可选择的加工机器数量.

目标函数（1）表示最小化所有工件的最大完工时间，即Makespan.约束（2）限制了每个工件的最大完工时间不早于任意一道工序的完工时间.约束（3）表示每个工件在机器上的开始加工时间取决于AGV运输工件到达的时间和该机器上一道工序结束加工时间的较大值.约束（4）表示每个工件在机器上的加工完成时间等于开始加工时间和所需加工时间之和.约束（5）表示每个工件的任意一道工序的加工开始时刻不小于上一道工序的结束加工时间.约束（6）表示各工件的开始运输时间至少大于其结束加工时间.约束（7）表示每个工件开始运输的时间取决于AGV到达机器的时间和加工完成时间的较大值.约束（8）表示每个工件的结束运输时间等于开始运输时间和AGV在机器间的移动时间之和.约束（9）表示同一时刻任意一道工序只能在一台机器上加工.约束（10）表示同一时刻任意一辆AGV只能运输一个工件.约束（11）表示同一时刻任意一辆空闲AGV的位置只能是一个站台.约束（12）限制了决策变量的取值范围.

2 自适应樽海鞘群算法

2.1 基础樽海鞘群算法

在组成樽海鞘链的所有个体中，根据每个个体在樽海鞘链中的位置可以将其分为2类：领导者和跟随者.领导者是位于链条前部的樽海鞘个体，其余的樽海鞘个体是跟随者.领导者负责带领其他个体在搜索空间内寻找食物源，跟随者在领导者的带领下进行局部搜索.2类樽海鞘个体间通过互相协作运动，达到寻找食物源（即全局最优解）的目的.基础樽海鞘群算法（SSA）的算法步骤如下.

1）种群初始化.随机初始化i个樽海鞘个体的位置xij，i=1,2,3,···,I，j=1,2,3,···,D.其中I为种群大小，D为空间维度.

2）根据目标函数计算每个樽海鞘个体的适应度，根据适应度对种群中的个体进行排序，拥有最优适应度的个体为食物源的初始位置.

3）对种群中樽海鞘个体的位置进行更新.领导者的位置更新按照下式：

式中：t为当前迭代次数；为当前代樽海鞘领导者i在第j维搜索空间的位置；Fj为当前代食物源在第j维搜索空间的位置；ubj和lbj分别为第j维空间的搜索上限和下限；c2和c3为[0,1.0]内分布的随机数，c2决定领导者在第j维空间搜索时移动的步长，c3决定领导者移动的正负方向；c1随着迭代次数的增加而降低，

式中：t为当前迭代次数，tmax为最大迭代次数.追随者顺次跟随前者进行移动，位置更新公式为

式中：为当前代樽海鞘跟随者i在第j维搜索空间的位置，(t-1)和(t-1)分别为上一代中跟随者i和跟随者i-1在第j维搜索空间的位置.

4）对计算得到的所有樽海鞘个体的每一维位置进行上、下边界处理，更新每个个体的适应度，用全局最优适应度对应的个体替换食物源的位置.

5）判断是否满足停止迭代的条件.若满足，则输出结果；否则，转步骤3）继续下一轮迭代.

2.2 自适应樽海鞘群算法

2.2.1 编码与解码策略 由于考虑运输时间的柔性作业车间调度问题涉及工序、机器和AGV 3个维度，基于3层编码方式构建调度解，分别为工序排列编码（operation code，OC）、机器选择编码（machine selection code，MSC）和AGV选择编码(AGV selection code，ASC).工序排列编码中的各元素表示工件的编号，工件号在编码中从左到右的出现次数对应工件的工序数；机器选择编码和AGV选择编码中的各元素分别表示工件工序对应选择的加工机器编号和AGV编号.如图1所示为由3个工件、2台加工机器和2辆AGV组成的柔性作业车间的一个可行的调度编码方案.

图1 编码方案Fig.1 Coding scheme

在初始化生成个体的工序排列编码时，工序排列编码是解空间中的离散点，而SSA算法更适合用来解决连续解空间的问题，因此采用基于随机密钥[1]的方式将编码的离散解空间连续化.对于有N个工件在M台机器上加工，考虑运输时间的柔性作业车间调度问题，每个樽海鞘个体都可以表示为M×N的向量并对应该问题的一个调度解，樽海鞘个体位置的每一维对应一道工序，用一个[0,1.0]的随机数表示，该随机数对应的工序是按照所有工件的工序排列确定；再将随机数按照从小到大的顺序排列，可得该个体的工序排列编码.如图2所示，采用随机密钥的方式，生成图1中对应的工序编码.

图2 工序排列编码的生成方式Fig.2 Generation method of operation code

在确定了工序排列编码后，需要确认机器选择编码和AGV选择编码.若采用排序编码的随机选择方式，则会产生一定数量的无效解，无法满足AGV设备的移动与加工工序之间的耦合约束，导致种群质量下降.基于启发式的解码方式，根据初始化个体的每道工序安排最早运输的AGV和最早加工完成的机器，具体步骤如下.

1）遍历初始化的工序排列编码的每道工序，判断该工件的上一道工序的加工机器位置是否有空闲AGV.若有，则选择该AGV进行搬运；否则选择到达该加工机器移动时间最少的AGV进行运输，直到安排完所有工序，可以确定AGV选择编码.

2）在确定AGV选择编码后，遍历工序排列编码的每道工序.在满足AGV资源约束和加工机器约束的条件下选择最早完成加工的机器，直到安排完所有工序，可以确定机器选择编码.

2.2.2 惯性权重策略 从式（15）可知，在基础SSA算法中，跟随者的位置每次迭代只由上一次迭代的第i-1只个体和第i只个体的位置确定.这虽然是樽海鞘群体行为的数学模型体现，但式（15）体现的是盲目跟随的行为.基础SSA算法没有考虑前一个跟随者对后一个跟随者的影响，在迭代过程中只是单向地接受历史信息来更新后者的当前位置，这会限制算法在迭代后期的搜索效率.

引入与迭代次数相关的非线性递减惯性权重来，评估第i-1只跟随者对第i只跟随者的影响程度.自适应地调整迭代前期和后期搜索侧重方向，使得领导者个体更好地引导跟随者个体进行搜索.在迭代前期，后一个跟随者受前一个跟随者的影响较大，能够快速地搜索到全局最优解的附近区域.在迭代后期，由于大部分樽海鞘个体已搜索到较优值，降低前者对后者的影响，可以使得跟随者在较优解的附近深度搜索，提升算法的收敛精度.惯性权重的计算方式如下：

结合式（15）、（16）可知，新的樽海鞘跟随者的位置更新公式为

式中：ω为基于Tanh函数构造的非线性递减变量，值域为[0.238 4,1].

2.2.3 自适应更新领导者-跟随者种群数量策略在基础SSA算法中，樽海鞘群体的领导者数量和跟随者数量通常设置为固定值，这使得在迭代前期，领导者数量过低导致算法全局寻优能力下降，容易早熟收敛.在迭代后期，跟随者数量过低导致算法局部搜索能力下降，寻优精度不高.固定种群数量的方法未充分考虑每轮迭代的个体位置、适应度和种群所处实际环境等因素，无法体现群体行为的自适应搜索过程.

针对该问题，提出基于种群更新成功率的自适应更新领导者-跟随者种群数量策略，使得樽海鞘领导者和跟随者的数量可以根据种群每次迭代的状态自适应地进行调整.种群更新成功率的定义如下.

式中：F(i,t)表示樽海鞘个体i在第t次迭代中是否搜索到了更优的解；表示迭代至第t次时，樽海鞘个体i的历史最优位置；α(t)表示当前迭代结束时，历史最优位置对应的适应度降低的个体数目占种群大小的比例.

为了减少迭代初期和后期种群更新成功率可能存在的不稳定取值对搜索造成的影响，定义与迭代次数相关的非线性递减系数：

结合式（18）、（20），可得自适应更新领导者-跟随者种群数量的计算公式：

式中：Ilea(t)和Ifol(t)分别为第t次迭代时计算得到的领导者和跟随者的数量；q为扰动系数，能够结合rand()函数对计算结果进行扰动，经过前期大量实验发现，q= 0.3时的搜索效果最好.

通过式（21）、（22）可知，在迭代前期，较多个体分散于搜索空间内，适应度降低的个体较多，导致α(t)较大，增加领导者种群的数量有利于增强算法的全局搜索能力.在迭代后期，樽海鞘个体逐渐聚集在最优解区域附近，导致α(t)较小，此时结合λ(t)自适应地减少领导者的数量，可以增加跟随者的数量，使得算法能够在最优解附近深度搜索，保持较强的局部探索能力，从整体上兼顾算法的全局寻优和局部搜索性能.

2.2.4 禁忌搜索策略 为了增强算法的邻域搜索能力，避免早熟收敛，引入禁忌搜索策略，在每轮迭代后对每个个体的工序排列编码、机器选择编码和AGV选择编码的邻域分别进行探索.算法只在符合加工工序约束的解中进行搜索，步骤如下.

1）工序排列编码邻域搜索.随机选择加工机器k和生成操作子r(r∈{1,2,3})，通过机器k的位置索引随机选择对应的第i个和第j个位置的工序.根据r的取值确定工序排列编码的邻域搜索方法，将{k,i,j,r}存入工序禁忌表.如图3所示为工序排列编码邻域搜索采用的前插、后插和交换3种操作.由于工序排列编码是由樽海鞘个体位置向量解码而成，算法在对工序排列编码执行邻域搜索操作时，对向量中的对应值执行相同操作，由此实现从离散解空间编码映射到连续解空间编码.

图3 工序排列编码的邻域搜索操作Fig.3 Neighborhood search operator of operation code

2）机器选择编码邻域搜索.随机选择工件i，在工件i的所有工序中随机选择一道工序j，在所有可加工机器中随机选择机器l替换原工序位置的机器k，将{k,i,j,l}存入机器禁忌表.

3）AGV选择编码邻域搜索.随机选择工件i，在工件i的所有工序中随机选择一道工序j，在所有可选择运输AGV中随机选择AGVp替换原工序位置的AGVs，将{s,i,j,p}存入AGV禁忌表.

4）对搜索得到的工序排序编码、机器选择编码和AGV选择编码计算得到适应度，判断是否优于原编码方案的适应度.若是，则替换原编码方案，更新个体历史全局最优解，并清空该个体的禁忌表.否则，对下个个体进行搜索，直至所有个体遍历完毕.

如图4所示为采用禁忌搜索策略的邻域搜索方法的流程图.

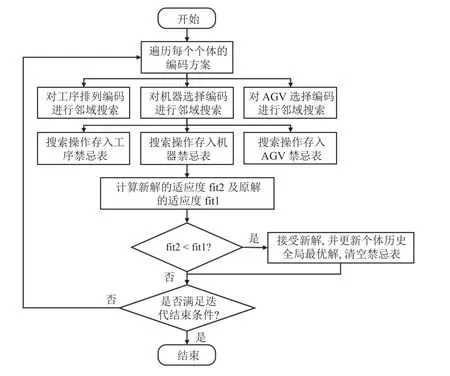
图4 邻域搜索的流程图Fig.4 Flow chart of neighborhood search

2.2.5 自适应樽海鞘群算法的流程 基于设计的算法策略，对基础樽海鞘群算法改进后得到的自适应樽海鞘群算法的算法流程如图5所示.

图5 自适应樽海鞘群算法的流程图Fig.5 Flow chart of adaptive salp swarm algorithm

1）初始化算法参数，包括种群规模I、初始迭代次数、tmax、扰动系数q、初始种群更新成功率α(0).

2）结合2.2.1节的3层编码策略，生成初始种群.

3）采用式（17）、（21），更新樽海鞘链中的个体位置和种群领导者数量.

4）计算个体适应度，使用2.2.4节的禁忌搜索策略对当前种群个体进行深度搜索，计算当前迭代种群的更新成功率α(t).

5）判断算法是否达到最大迭代次数限制.若未达到，转至步骤3）；否则，输出最优解及目标值.

2.2.6 时间复杂度分析 对于需要求解的优化问题，假设目标函数的计算量为Cof，解空间维度为D，樽海鞘种群大小为I.根据基础SSA算法的求解步骤及时间复杂度的计算方法可知，基础SSA算法的时间复杂度为O(tmax(ID+I·Cof)).

根据2.2.5节的算法步骤可以看出，α(t)、ω、种群数量更新和禁忌搜索是ASSA算法增加的计算步骤.根据时间复杂度的计算规则可知，在一次迭代中，这些步骤对应的时间复杂度分别为O(I+1)、O(1)、O(2)和O(ID).在tmax次迭代后，ASSA算法的时间复杂度为O(tmax(2ID+I·Cof+I+4))，在忽略高阶项的系数和低阶项后，ASSA算法的总时间复杂度为O(tmax(ID+I·Cof))，与基础SSA算法的时间复杂度属于同一数量级.采用提出的改进策略不会额外增加算法的计算开销，在设计上保证了算法搜索过程的高效性，使得算法的计算效率不会下降.

3 实验结果与分析

3.1 实验设计

为了验证提出算法的性能，在硬件为i7-10710U、内存为16 GB、操作系统为WIN10的PC机上采用Python语言实现了算法.仿真算例采用Bilge等[18]提出的部分案例，使用加工机器与装载站台组成4种布局.所有案例分为2类：1）第1类案例命名如“EX12”，表示工件组为jobset1，布局为layout2；第2类案例命名如“EX120”，表示工件组为jobset1，布局为layout2，0表示案例设置的运输时间和加工时间比值的标识.算法的参数设置如下：种群数量为100，算法的最大迭代次数为1 000，设置100代内最优解无更新，则退出迭代，每组实验运行10次.统计指标top表示算法的运行时间，单位为s；Cmax为算法运行得到的最优解；表示算法运行10次得到的Cmax平均值；δ为结果的相对百分比偏差，计算方式如下：

3.2 改进策略有效性的分析

为了说明提出的改进策略的有效性，将采用惯性权重策略的樽海鞘群算法记作WSSA，采用自适应领导者-跟随者种群数量更新策略的樽海鞘群算法记作LSSA，采用禁忌搜索策略的樽海鞘群算法记作TSSA，综合改进后的樽海鞘群算法记作ASSA，选取EX11-EX51及EX64-EX104共10个案例进行测试.算法在每个案例上运行10次，得到的解质量对比结果如表1所示.

表1 不同改进策略的加工完成时间对比结果Tab.1 Comparison results of makespan with different improved strategies

从表1可以看出，本文提出的ASSA算法在全部案例中取得的最优解均较好.比较WSSA算法与SSA算法可知，WSSA有4个案例的最优解好于SSA算法，3个案例的最优解与SSA算法相同，这说明惯性权重策略能够在SSA算法的基础上明显改善算法的全局和局部探索能力，但在迭代后期有陷于过早收敛的可能性，导致结果变差.比较LSSA算法与SSA算法可知，LSSA算法有3个案例的最优解好于SSA算法，6个案例的最优解与SSA算法相同，LSSA所有案例PRD结果的平均值优于SSA算法，这说明LSSA算法在迭代后期可以在最优解附近深度搜索，从而保持较强的局部探索能力.比较TSSA算法与SSA算法可以看出，TSSA算法有6个案例的最优解好于SSA算法，2个案例的最优解与SSA算法相同，这说明引入禁忌搜索策略能够有效避免算法在后期计算中陷入局部最优，改善解的质量.

如图6所示为采用不同改进策略的樽海鞘群算法求解EX104的收敛曲线.可以看出，在相同参数设置的情况下，ASSA算法综合体现了改进策略的优势，有效地平衡了算法的全局探索和局部搜索能力，能够不断地在较短的迭代周期内搜索到更优的解，提升了算法的收敛速度和收敛精度，证明本文提出的改进策略对于求解该类调度问题是有效的.

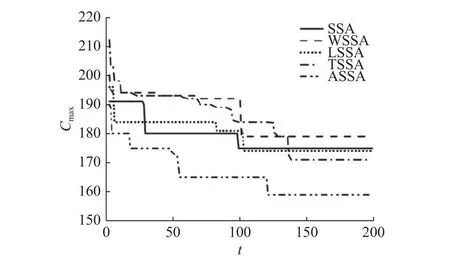
图6 采用不同改进策略求解EX104的收敛曲线Fig.6 Convergence curves of solving EX104 with different improved strategies

3.3 自适应樽海鞘群算法性能的对比

为了进一步验证ASSA算法的有效性，选择AGA算法（adaptive genetic algorithm）[6]、IDSSA算法（improved discretized salp swarm algorithm）[14]、AAADE算法（artificial algae algorithm with differential evolution）[19]和MOGWO算法（multi-objective grey wolf optimization）[20]进行对比.4种算法均使用原文推荐参数进行测试，结果如表2、3所示.为了验证提出的模型和算法求解最优解的性能，使用GUROBI求解器（Gurobi solver）与ASSA算法获得的结果进行对比，GUROBI的运行上限时间设置为600 s，结果如表4所示.

表2 不同优化算法的实验测试结果（＞0.25）Tab.2 Comparison results of different optimization algorithms (＞0.25)

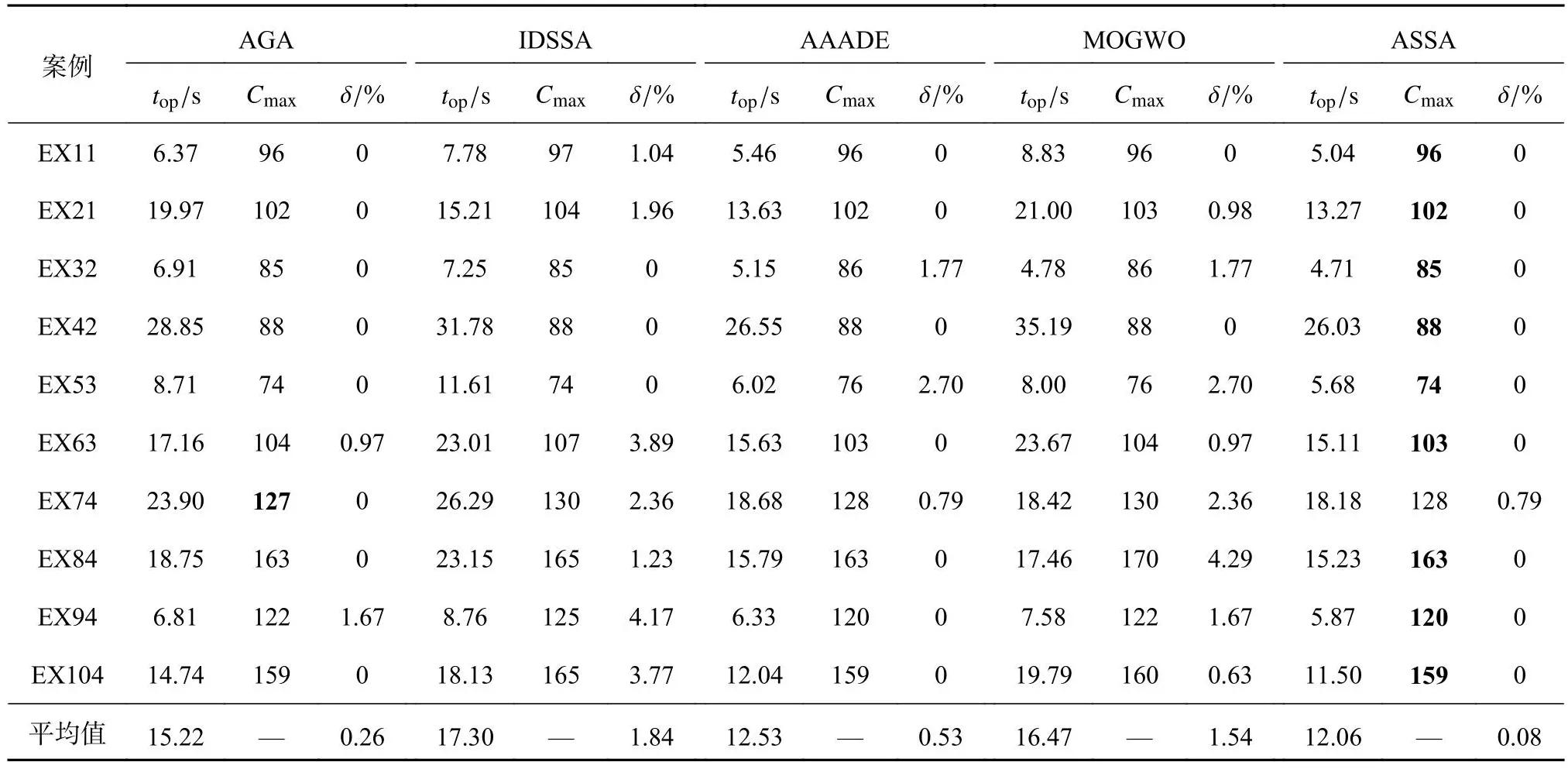
表2 不同优化算法的实验测试结果（＞0.25）Tab.2 Comparison results of different optimization algorithms (＞0.25)

案例AGAIDSSAAAADEMOGWOASSA images/BZ_14_462_652_525_690.png images/BZ_14_584_651_651_684.pngimages/BZ_14_706_651_764_684.pngimages/BZ_14_836_652_898_690.png images/BZ_14_958_651_1025_684.png images/BZ_14_1079_651_1138_684.pngimages/BZ_14_1210_652_1272_690.png images/BZ_14_1332_651_1398_684.png images/BZ_14_1453_651_1511_684.pngimages/BZ_14_1583_652_1646_690.png images/BZ_14_1705_651_1772_684.png images/BZ_14_1827_651_1885_684.pngimages/BZ_14_1957_652_2019_690.png images/BZ_14_2079_651_2146_684.png images/BZ_14_2200_651_2259_684.pngEX116.379607.78971.045.469608.839605.04960 EX2119.97102015.211041.9613.63102021.001030.9813.271020 EX326.918507.258505.15861.774.78861.774.71850 EX4228.8588031.7888026.5588035.1988026.03880 EX538.7174011.617406.02762.708.00762.705.68740 EX6317.161040.9723.011073.8915.63103023.671040.9715.111030 EX7423.90127026.291302.3618.681280.7918.421302.3618.181280.79 EX8418.75163023.151651.2315.79163017.461704.2915.231630 EX946.811221.678.761254.176.3312007.581221.675.871200 EX10414.74159018.131653.7712.04159019.791600.6311.501590平均值15.22—0.2617.30—1.8412.53—0.5316.47—1.5412.06—0.08

表3 不同优化算法的实验测试结果（）Tab.3 Comparison results of different optimization algorithms ()

表3 不同优化算法的实验测试结果（）Tab.3 Comparison results of different optimization algorithms ()

案例AGAIDSSAAAADEMOGWOASSA images/BZ_14_473_1848_535_1886.png images/BZ_14_594_1847_661_1880.pngimages/BZ_14_714_1847_773_1880.pngimages/BZ_14_844_1848_907_1886.png images/BZ_14_965_1847_1032_1880.png images/BZ_14_1086_1847_1144_1880.pngimages/BZ_14_1216_1848_1278_1886.png images/BZ_14_1337_1847_1404_1880.png images/BZ_14_1458_1847_1516_1880.pngimages/BZ_14_1587_1848_1650_1886.png images/BZ_14_1709_1847_1775_1880.png images/BZ_14_1829_1847_1887_1880.pngimages/BZ_14_1959_1848_2021_1886.png images/BZ_14_2080_1847_2147_1880.png images/BZ_14_2201_1847_2259_1880.pngEX1101.3312601.7612600.7012600.9112600.361260 EX2101.6814801.9014800.8214801.0614800.441480 EX3201.3814501.781482.070.8414501.5714500.461450 EX4209.50114010.3111406.8511407.7911406.401140 EX5301.329901.129900.539901.099900.19990 EX6305.8218207.2218205.1218208.3418204.651820 EX7404.9913705.2413703.1213703.8513702.651370 EX8401.4929302.292940.340.7829301.0629300.282930 EX9408.27175011.5017506.51175012.2417506.121750 EX104033.25240037.28240024.98240043.53240024.492400平均值6.9—0.08.04—0.245.03—0.08.14—0.04.6—0.0

表4 ASSA算法与GUROBI求解器的实验测试结果Tab.4 Comparison results of ASSA algorithm and GUROBI solver

从表2、3的统计结果可以看出，在应用提出的ASSA算法求解第1类案例时，有9个案例的最优解优于AGA算法，所有案例的最优解均优于其他3种对比算法；在应用ASSA算法求解第2类案例时，ASSA算法均能在更短时间内获得与对比算法一致的结果.统计运行时间可知，ASSA算法在求解2类案例时的平均运行时间是所有算法中最少的.在对比2类案例的δ平均值时可以看出，采用ASSA算法获得的结果在第1类和第2类案例中均最小，尽管在第2类案例中AGA算法δ的平均值与ASSA算法相同，但ASSA算法能够在更短的运行时间内获得最优解.

从表4的统计结果可以看出，ASSA算法能够在更短时间内找到与GUROBI一致的最优解.GUROBI分别需要平均运行147.89和26.38 s进行迭代求解，ASSA算法的平均运行时间只需要12.06和2.26 s，显示了调度模型和ASSA算法搜索精确解的可靠性和高效性.

综合来看，在所有的测试案例中，利用ASSA算法能够较好地在更短时间内求解可行解，这说明ASSA在面对不同的调度场景时，有更大的概率可以搜索到最优解，具有良好的搜索性能，能够更加高效地获得更好的调度结果.实验测试结果表明，本文提出的ASSA算法与AGA算法、IDSSA算法、AAADE算法和MOGWO算法相比，具有更高的计算效率和寻优性能，在求解考虑运输时间的柔性作业车间调度问题方面具有较明显的优势，是鲁棒、高效的求解算法.

3.4 AGV数量对完工时间的影响

在含有AGV的柔性作业车间中，AGV的数量对于调度效率的提升有着至关重要的影响.为了研究该问题，引入经济学中的边际效应理论[21]，分析AGV数量对实验案例完工时间的影响程度.

边际效应（marginal utility, MU）是指每新增或减少一个单位的商品或服务，它对商品或服务的收益增加或减少的效用.在本文所涉及到的研究中，商品指AGV，收益是指完工时间（makespan）.评估AGV边际效应的计算公式如下：

式中：ΔCmax为完工时间的差值，ΔS为AGV数量的差值.

选用EX11～EX101共10组案例，在设置不同AGV数量的条件下分别计算对应的完工时间，每组案例运行10次，统计结果如表5所示.将表5的结果通过式（24）进行转化计算，绘制得到各案例的AGV边际效应曲线，如图7所示.

表5 不同数量AGV的实验测试结果Tab.5 Comparison results of using different number of AGV

图7 各案例的AGV边际效应曲线Fig.7 AGV marginal utility curve of each case

表5和图7表明，随着车间内AGV数量的增加，总完工时间呈现下降的规律，但每增加一辆AGV，边际效应呈现递减的规律.当AGV数量增加到6时，边际效应降低为0，此时完工时间不再受到AGV数量的影响，主要受到加工工序和加工时间的约束，所以增加AGV的数量无法进一步提升车间的调度效率.基于以上分析可知，当确定每个调度场景下最合适的AGV数量时，需要综合考虑成本、效率、完工时间等因素.

4 结 语

针对考虑运输时间的柔性作业车间调度问题，本文提出自适应樽海鞘群算法ASSA.设计基于随机密钥的3层编码方式，将编码的离散解空间连续化，引入惯性权重评价跟随者之间的相互影响程度.提出自适应更新领导者-跟随者种群数量策略调整种群数量，引入禁忌搜索策略，使得算法具有较强的局部搜索能力.通过与其他智能优化算法和求解器的对比，证明了ASSA在求解此类问题方面具有明显优势.此外，发现完工时间的提升效率随着AGV数量的增加呈现递减规律.下一步工作将针对各类生产调度问题开展进一步研究，如多目标优化问题、考虑充电这些实际约束下的车辆调度问题.