多机器人路径规划及编队控制策略

屈军锁,马玉环,蔡 星,李鹏飞

(西安邮电大学 通信与信息工程学院,陕西 西安 710121)

工业化进程的加快使得机器人技术的发展愈发被重视。机器人技术[1]是对未来新兴产业发展具有重要意义的高技术之一,现已广泛应用在工业、医疗和科学探索等众多领域。随着需求的多样化和复杂化,单机器人在许多场景下已无法满足需求,而多机器人技术开拓了机器人领域的新方向,弥补了单机器人的缺陷。多机器人系统可以通过机器人之间相互合作共同完成复杂的任务,比单机器人系统更灵活、稳定性表现更好[2]。目前,多机器人的编队控制问题已成为机器人领域的重要研究方向。多机器人编队控制问题源于自然界生物的群体行为,如鸟群的集体迁徙行为、鱼群编队防御行为和蚁群集体协作觅食行为等。在机器人领域,多机器人编队是指多个移动式机器人在运动过程中,按照一定的距离和运动状态的约束,使得多机器人形成期望的几何形状[3],如工业中利用仓储机器人协同搬运货物、军事中利用多无人机协同作业等[4]。

多机器人系统的控制结构主要包含集中式、分散式和分布式等3类,其中分布式结构包含了集中式与分散式结构的优点,应用较为广泛。多机器人编队的控制方法主要有领航者-跟随者编队控制策略[5]、基于行为的编队控制策略[6],以及基于虚拟结构的编队控制策略[7]。领航者-跟随者编队控制策略具有结构简洁易于实现的优点,但编队稳定性受到领航者状态的影响较大[8]。文献[9]在领航者-跟随者策略的基础上提出了基于拍卖算法的编队控制策略,提高了编队的效率,但是该策略对于系统资源消耗较大。文献[10]引入了虚拟领航者,使得编队中跟随者相对于领航者的跟踪误差更小。基于行为的编队控制策略适用于机器人数量较多的系统,但编队队形的稳定性和实时性方面存在缺陷。基于虚拟结构的编队控制策略[11]编队精度较高,但在实际中的通信与计算成本较大,编队实时性较差。文献[12]针对多机器人的编队运动问题,提出一种链式编队控制方法,该方法通过主从协同的方式实现了多机器人的编队行进,但编队稳定性较差。文献[13]针对未知环境下的多机器人编队队形控制问题,基于类鸟群模拟放射方法设计了不同规则的控制器,能够实现机器人编队任意队形的变换和保持,但是该方法计算复杂度较高。

近年来,一致性理论在编队控制领域的应用逐渐受到重视。Ren等[14]将一致性控制律应用于多智能体系统的编队控制问题中,并验证了基于领航-跟随者策略等几种传统编队策略均可利用一致性理论实现。基于符号拉普拉斯矩阵的多机器人仿射编队控制方法[15]分析了多机器人系统能够实现仿射变换的条件,为多机器人的编队控制提供了一种新的方法。文献[16]研究了对应于无向图应力矩阵的仿射编队控制方法,给出了机器人编队能够实现仿射定位的充要条件,基于仿射变换设计了不同情况下的编队控制器,并证明了所提出的控制律的稳定性和全局收敛性。然而,各种策略均存在着各自的局限性和不足,限制了其在复杂场景下的广泛应用。因此,拟对多机器人路径规划以及编队运动控制问题进行研究,给出一种多机器人路径规划及编队控制策略。首先,基于IPOPT(Interior Point Optimizer)路径优化方法,改善A*算法规划的路径不平滑问题,得到轨迹平滑的路径。然后,根据有向图结构给出领航-跟随者型仿射编队控制方法,并基于一致性理论设计一阶和二阶多机器人系统的编队运动控制协议,实现机器人编队队形的控制。

1 系统设计

将多机器人编队视为一个尺度可伸缩的整体,参照单机器人的路径规划方法,由编队中的领航者负责规划编队整体的参考路径,根据编队中机器人之间的位置关系对获得的路径偏移,得到全部机器人的路径。选择A*算法[17]作为多机器人编队的路径规划算法,基于IPOPT对A*算法规划的全局路径进行优化,得到轨迹平滑的路径。基于有向图结构,给出领航-跟随者型仿射编队控制方法,实现编队的放缩、旋转等变换。系统流程如图1所示。

图1 系统流程

1.1 A*算法优化

1.1.1 A*算法

A*算法[17]是一种静态路网中求解最短路径搜索算法,通过增加启发式函数确定最优路径,是目前应用较为广泛的路径查找算法。A*算法的公式描述为

F(n)=g(n)+h(n)

(1)

其中,

式中：F(n)为节点n的估价函数;g(n)为结点t的实际代价;h(n)为从结点n到目标节点p的最佳路径的估计代价;(xn,yn)为节点n的坐标;(xt,yt)为节点t的坐标;(xp,yp)为节点p的坐标。

通过仿真软件对A*算法进行路径规划仿真,A*算法路径规划过程如图2所示,规划结果如图3所示。

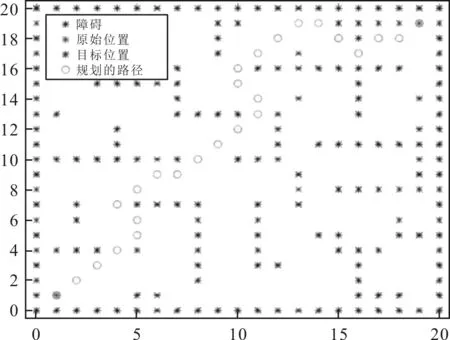
图2 A*算法路径规划

图3 A*算法路径规划结果

观察图2和图3仿真结果发现,A*算法能够从起点位置搜索出到达目标位置的无碰撞路径,但是路径的转折角度过大,路径不够平滑。

1.1.2 基于IPOPT的A*算法轨迹优化

为了使得A*算法规划的路径更加平滑,基于IPOPT对A*算法规划的全局路径进行优化,将线性搜索过滤原始对偶内点算法用于求解非线性方程组。内点算法是将非线性规划的不等式约束转化为障碍并将其添加到目标函数中,将原始的非线性规划转化为仅等式约束或无约束问题。简化后,非线性优化问题便转换为障碍因素类型的子问题。

非线性优化的问题模型表示为

(2)

s.t.gL≤g(x)≤gU
xL≤x≤xU

式中：x∈Rn为优化变量,下限xL∈(R∪{-∞})n,上限xU∈(R∪{+∞})n;函数f：Rn→R为目标函数;函数g：Rn→Rm为一般非线性约束,其上限gL∈(R∪{-∞})m,下限gU∈(R∪{+∞})m。将式(2)中的约束g(x)和变量x提取为如下形式

(3)

将式(3)中所有的变量下限为0,那么原非线性规划式(2)可以转换为一个新的非线性规划问题

s.t.c(x)=0

x≥0

(4)

式中：函数f(x)为目标函数;函数c(x)为约束函数,其约束条件为ci(x)=gi(x)-si=0,(i=1,2,3,…n);x≥0为添加新的约束,使得所有变量的下限等于0。在这个新的非线性规划问题中,使用内点法并引入对数障碍项,构建得到新的目标函数

s.t.c(x)=0

(5)

式(5)中,对数障碍函数φμ(x)替代了式(4)中c(x),μ为障碍项参数且μ>0。φμ(x)将x的分量xi添加到目标函数中,从而保证了xi≥0,在优化过程中,任意xi保持非负。考虑到xi趋于0时,φμ(x)的值将区域无穷大,因此式(5)的最优解将出现在x的定义域内,且满足xi≥0。

原非线性优化问题的求解可以转换为φμ(x)的最小值求解问题,求解步骤如下。

步骤1确定合适的障碍参数μ,为变量x赋初始值。

步骤2把μ的值减少,求解下一个障碍问题,起始点为前一个障碍问题的解。

步骤3不断重复步骤2,直到得到式(4)的解,或者满足一阶最优条件的解。

求得式(5)的一阶的最优条件为

(6)

式中：x,z≥0;e为全1向量;y∈Rn为拉格朗日乘子;z∈Rn为边界约束的拉格朗日乘子;X=Diag(x),Z=Diag(z)。

(7)

式中：I为单位矩阵;Wi为式(3)中gi(x)的拉格朗日函数的海森矩阵;Ai为等式约束的雅克比矩阵的转置;gi为目标函数的梯度。

在zi方向上更新时满足

其中,τ=min{0.99,μ}。

(8)

设约束条件为g、状态变量为x,那么使用IPOPT求解非线性优化问题的主要步骤描述如下。

步骤1设置状态变量x和约束条件g的数量。

步骤2设置状态变量x的初始值。

步骤3设置状态变量x和约束条件g的上下界。

步骤4构建约束条件g。

步骤5构建问题的目标函数。

步骤6设置IPOPT求解参数。

步骤7迭代求解,得到优化结果。

优化后的路径贴近原始路径,且路径弯折区域轨迹平滑连续,使得机器人在该路径上的运动连续,降低了机器人的运动代价。基于IPOPT的A*轨迹优化过程如图4所示。

图4 基于IPOPT的A*轨迹优化过程

1.2 仿射编队设计

仿射变换是指一个向量空间通过线形变换与平移变换组合,转换为另一个向量空间的变换过程。图形的仿射变换如图5所示。

图5 图形仿射变换

二维平面中的一个多机器人编队,如果编队变换前后的队形仿射等价,那么编队队形变换过程可以被仿射变换描述,编队可以基于仿射变换生成任意与之仿射等价的队形。

设d维空间d中由N个机器人组成多机器人系统,前Nl个机器人为领航者,跟随者数量为Nf=N-Nl,则系统中机器人的位置集合可表示为

(9)

式中：pl(l=1,2…Nl)为系统中领航者的位置集合;pf(f=Nl+1,Nl+2,…N)为跟随者的位置集合。

系统中机器人之间通信拓扑用有向图G=(V,E)表示,其中：V=(Vl,Vf)为节点集;Vl表示领航者集合;Vf表示跟随者集合;E⊆V×V为边集,若图中存在有向边(i,j)∈E,那么节点j定义为节点i的入邻居,节点i为j的出邻居。系统编队表示为(G,p),有向图G的节点与系统中的机器人依次对应。

标称编队描述了编队的期望队形,定义系统的标称编队表示为(G,r),r为标称编队的队形矩阵,表示为

(10)

式中：rl为领航者的标称队形;rf为跟随者标称编队。

定义标称队形r的仿射映射为

(11)

式中：(A,b)记作仿射变换;IN与1N分别为N维单位矩阵和全1向量;⊗为克罗內克积。

定义位置集合p的配置矩阵P(p)∈d×N,定义P(p)的增广矩阵为

(12)

定义时变目标编队为

p*(t)=[Id⊗A(t)]r+1N⊗b(t)

(13)

式中：Id为d维单位矩阵;A(t)表示仿射变换中的线性变换,而b(t)则仿射变换中的平移变换;t为时间参数。

文献[16]给出了无向图结构下的标称编队能够实现仿射定位的条件,那么根据无向图结构下的标称编队仿射定位的条件可以推导出有向图结构下标称编队(G,r)能够实现仿射定位的条件如下。

1) 系统中跟随者的位置集合pf总是能够被领航者的位置pl确定。

2) 对于有向图G的符号拉普拉斯矩阵LΩ及机器人位置集合p,满足

(LΩ⊗Id)p=0

(14)

其中,

式中,kij表示连接节点i与节点j的边的权重。

(15)

标称编队队形及其拓扑结构如图6所示,图6中标号1,2,3的圆形表示领航者机器人,标号4,5,6,7的圆形表示跟随机器人。

图6 标称编队队形

基于以上多机器人能够实现仿射定位的条件,设计一阶多机器人系统的运动控制协议,一阶多机器人系统中第i个机器人的动力学方程为

(16)

式中,ui(t)表示第i个机器人的控制输入。

设编队中领航者的速度为有界的时变值,设计编队中跟随机器人i的运动控制协议为

(17)

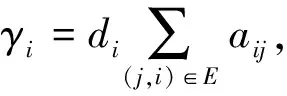
(18)

由此,根据文献[18]给出的一致性判定条件,式(17)所示的控制协议能使得系统中跟随机器人的位置跟随误差全局收敛于领航者。

设计二阶系统的运动控制协议,系统中机器人的二阶动力学方程为

(19)

式中,vi与ui分别表示系统中机器人的速度与控制输入,i=1,2,…N。对于二阶系统,控制输入为加速度。受文献[18]中关于二阶多机器人系统运动控制协议设计思路的启发,设编队中领航者的加速度为有界的时变值,则设计编队中第i个跟随机器人的运动控制协议为

(20)

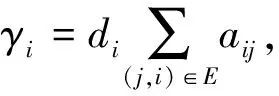
根据文献[18]给出的一致性判定条件,式(20)所示的控制协议能使得系统中跟随机器人相对于领航者的跟随误差全局收敛。

2 验证结果分析

2.1 路径优化仿真验证

首先利用A*算法规划出全局路径,基于IPOPT对获得的路径进行优化。由大小为22×22的栅格单元组成的封闭地图,地图中的障碍物随机生成。第一次仿真的起始点坐标设置为(3,18),目标点坐标(18,2),结果如图7所示。第二次仿真的起始点坐标设置为(3,18),目标点坐标设为(19,7),结果如图8所示。图中黑色栅格代表障碍物,连续曲线代表规划的路径。图7(a)与图8(a)分别表示第一次和第二次仿真的原始路径,图7(b)与图8(b)分别表示第一次和第二次仿真改进后的路径。

图7 路径优化第一次仿真结果

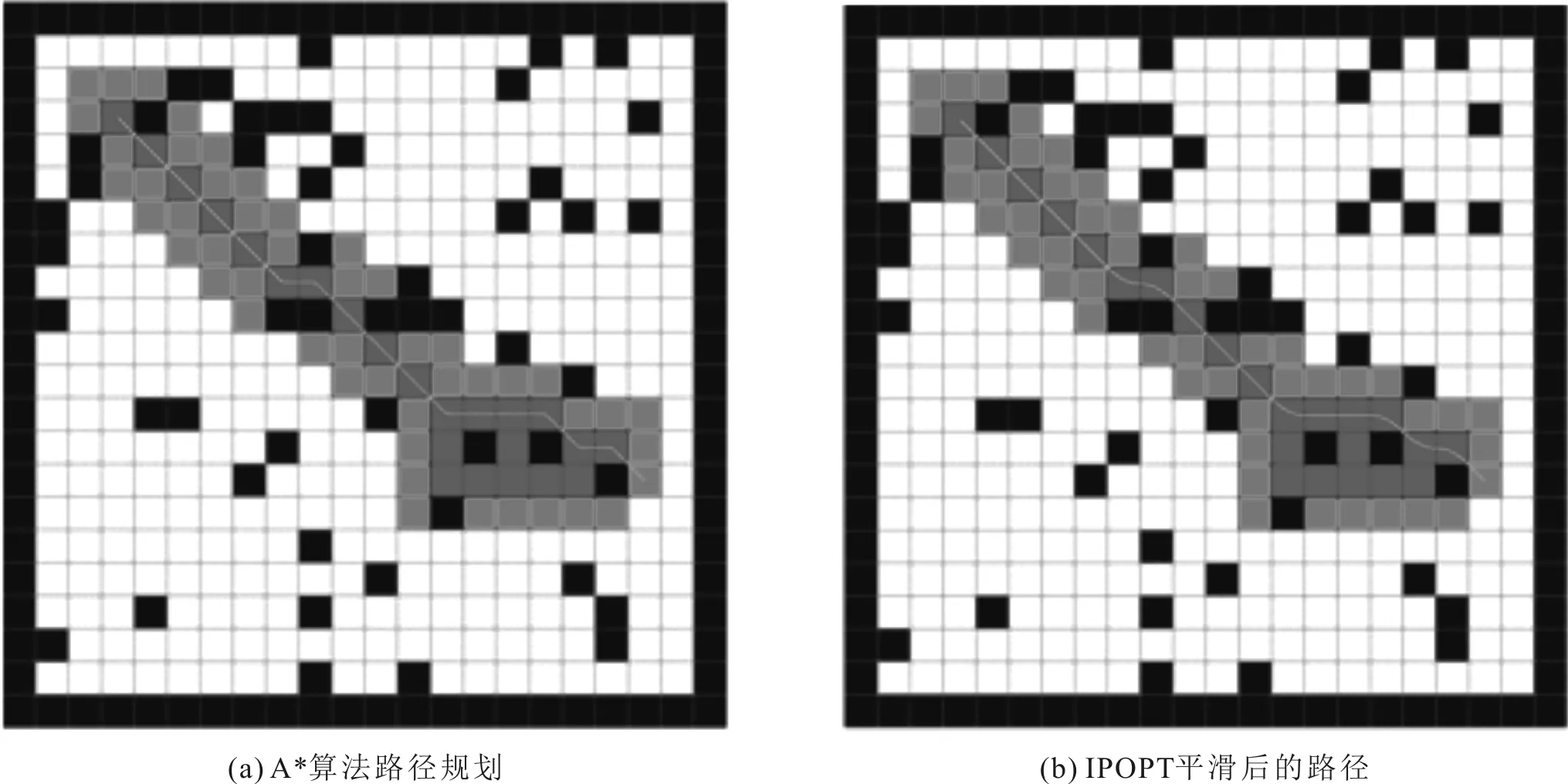
图8 路径优化第二次仿真结果

相比于图7(a)和图8(a)原始算法的路径,图7(b)和图8(b)中改进后的路径在靠近障碍物的区域没有出现角转弯,轨迹连续性比较好,且贴近原始路径。可以看出,基于IPOPT的轨迹平滑方案能够有效平滑A*算法规划路径中的转折区域。

2.2 编队运动规划及仿真

创建二维平面中大小为55 m×55 m的封闭有障碍地图,确定图6编队中前3个机器人作为领航者,领航者的初始位置为

跟随者的初始位置为

领航者的目标位置为

编队整体的路径规划步骤如下。

步骤1获取当前环境地图信息。

步骤2确定编队期望队形,根据期望队形确定3个领航者之间的相对位置关系。

步骤3由编队中第一个领航者利用 A*算法在当前环境中规划出平滑的全局路径,并基于IPOPT优化当前路径,将该路径发布给其余领航者。

步骤4编队中其余领航者根据与第一个领航者的相对位置关系以及环境中的障碍物分布信息,对步骤3中得到的路径进行坐标偏移,分别得到其他领航者的路径。

步骤5判断偏移后的路径轨迹是否与障碍物发生碰撞,规划编队的避障策略。

当编队中的领航者获得全局路径后,根据编队队形几何结构,规划领航者在当前路径下的速度与加速度等控制变量,进而进行运动规划。编队在当前环境下的运动轨迹如图9所示,图中红色圆形为编队的领航者,蓝色圆形为编队中的跟随者,绿色虚线为第一个领航者的路径,黑色区域为障碍物分布。

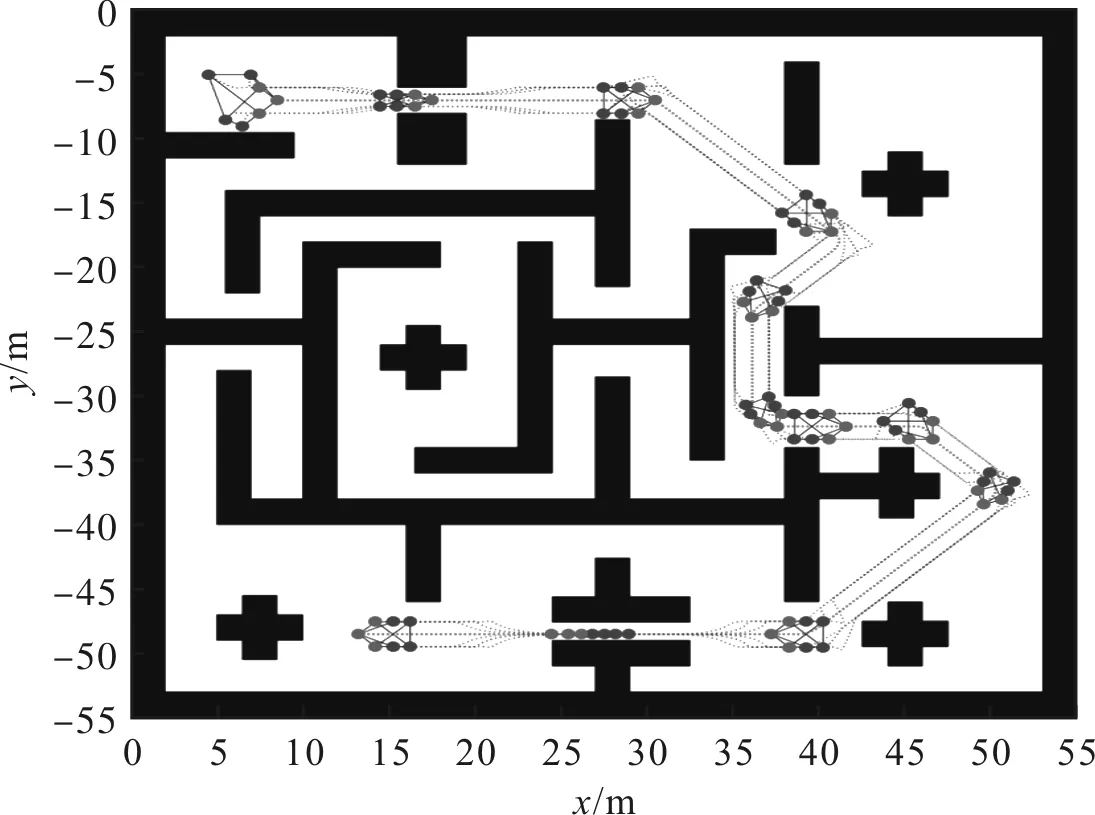
图9 编队运动轨迹

编队中各机器人在X轴与Y轴上位移、速度和加速度曲线分别如图10与图11所示,可以看出,系统中的领航者和跟随者机器人在X轴与Y轴上位移、速度和加速度等均平缓变化,未出现突变现象。

图10 X轴上位移、速度及加速度与时间的关系

图11 Y轴上位移、速度及加速度与时间的关系

3 结语

研究了多机器人编队的路径规划以及运动控制问题。基于IPOPT的路径优化方法改善了A*算法规划的路径转弯不平滑的问题。对于多机器人的编队控制问题,给出了基于有向图结构的领航-跟随型仿射编队控制方法,并设计了一阶和二阶系统的运动控制协议。实验结果表明,基于IPOPT的路径优化方法能够有效平滑A*算法规划的路径,且编队在沿着规划的路径运动时能够保持编队队形。