基于马氏距离聚类的高光谱图像波段选择方法

吴 青,徐 杰

(西安邮电大学 自动化学院,陕西 西安 710121)

遥感技术是自20世纪60年代发展起来的一种对地探测技术,该技术可以获取到更多的相关遥感数据,以用于分析地物特征和变化规律[1]。随着成像光谱仪的快速发展,遥感图像的光谱分辨率日益提高。高光谱遥感技术通过范围较大且间隔较窄的电磁波段获取感兴趣的地物信息[2]。与传统的彩色图像以及多光谱遥感图像相比,高光谱遥感图像(Hyperspectral Image,HSI)可以提供更加丰富的光谱信息,能更好地描述地物特征[3-4],为地物的识别与检测提供较大的便利。目前,高光谱遥感在环境监测、农业林业地面探测、城市建设、军事目标探测等各个领域均得到了广泛关注,成为遥感领域的前沿技术[5]。

近年来对HSI的研究大多是针对地物的分类与识别[6-7]。HSI为地物分类提供丰富光谱信息的同时,也带来了一些问题。例如,根据HSI成像原理,相邻光谱波段间存在较高的相关性,当处理高维的HSI数据时,大幅增加了时间和空间复杂度,容易导致“维数灾难”问题,因此,对HSI数据进行降维成为不可或缺的预处理步骤。

常用的HSI降维方法主要有特征提取[8-9]和波段选择[7]两种方式。特征提取方法主要是找到一种转换策略,将原数据映射到新的低维特征空间,以达到信息综合、特征增强以及光谱降维的效果。然而,一方面,特征提取方法是采用原始数据的所有波段进行数据转换,一些冗余或者噪声波段会对数据转换的结果造成一定程度的干扰;另一方面,该方法采取的是数据转换策略。该策略使得HSI原始数据的数值发生变化,数据丢失了原有的物理意义,导致关键信息丢失。波段选择方法的主要原理是从原始HSI数据中选取一个具有代表性的波段子集,以达到既能降低数据维度的目的,也可以保留原始数据固有的特性,这样更有利于后续与空间信息相结合。相对而言,目前主要通过波段选择方法对高维HSI数据进行降维。

依据使用先验信息的多少,可以将现有的波段选择方法分为无监督方法、半监督方法和监督方法等3类方法。无监督方法更适用于HSI波段选择。无监督的波段选择方法主要包括基于排序的方法[10]、基于子空间划分的方法[11]和基于聚类的方法[12]等3种方法。

基于排序的方法主要根据某个度量准则来评价每个波段的重要性,然后,根据度量准则对所有波段进行排序,从而选出排名靠前的波段。例如,文献[13]提出一种基于特征分析的波段优先级划分标准,即最大方差主成分分析(Maximum-Variance Programmable Counter Array,MVPCA),利用协方差矩阵的特征值和特征向量构建负载因子矩阵确定波段的信息含量。文献[14]提出了最佳指数法(Optimum Index Factor,OIF)。文献[15]提出一种正交投影波段选择方法(Orthogonal Projection Band Selection,OPBS),将最大椭圆体算法与序列前向搜索算法相结合来寻找有关波段。但是,总体而言,基于排序的波段选择方法大多数仅考虑到波段质量,并没有考虑波段间相关性,导致最终分类结果的准确性较低。

基于子空间划分的波段选择方法对波段之间的相关性和减小计算量均有所考虑。例如,文献[16]结合联合熵波段选择算法,提出了一种自动子空间划分(Auto-Subspace Partition,ASP)的改进方法,该方法实现了在删减冗余信息的同时选择出含有主要信息的特征波段组合,可以有效地减少相关性较高的波段。但是,基于子空间划分的波段选择方法通常没有考虑噪声波段对实验结果的影响,影响了最终分类结果的准确性。

基于聚类的波段选择方法可以有效减少波段间的相似性,例如,文献[17]提出一种基于密度峰值聚类的算法(Enhanced Fast Density Peak Clustering,E-FDPC),该算法对归一化局部密度和簇内距离进行加权计算,具有较高的分类精度。文献[18]提出一种最优聚类框架(Optimal Clustering Framework,OCF),该方法提供了一种自动确定所需波段数的方法,具有良好的鲁棒性。但是,经典的波段选择聚类方法大多利用波段间的欧氏距离作为相似性判别指标。利用欧氏距离来判别波段间的相似性往往容易受到各像素数据相关性的影响,在高维数据中应用容易失效,使得最终分类结果不够准确。

由于马氏距离考虑特征之间的相关性,在区分不同类别数据时更为准确[19],为了有效地提高高光谱图像波段的分类准确率,本文拟提出一种基于马氏距离聚类的波段选择方法(Band Selection Method Based on Mahalanobis Distance Clustering,BS-MDC)应用于高光谱图像的波段选择。首先,根据选择的波段数量对HSI数据全部波段进行粗分割;其次,利用基于马氏距离聚类的方法进行精细子空间划分,采用波段间的马氏距离来描述波段间的相似度,通过求每一个波段的噪声等级进行排序,选择出每一组中噪声等级最低的波段,组成最终的波段选择结果。该方法结合了基于子空间划分、基于马氏距离聚类和排序的波段选择方法,以减小聚类过程中的计算量,避免样本特征之间相关性对波段选择结果产生的影响,同时,也考虑了噪声波段对降维结果的影响。最后,分别使用支持向量机(Support Vector Machine,SVM)、K最近邻(K-nearest Neighbor,KNN)、极限学习机(Extreme Learning Machine,ELM)等3个分类器在两个真实数据集上进行实验验证。

1 背景知识

1.1 高光谱图像

HSI数据是一个光谱分辨率较高的三维立方体[20]。HSI的数据形式示意图如图1所示。在空间维度上,HSI数据可以看作是同一场景对应的上百个不同波段的光谱反射率所形成的二维图像的叠加,光谱维度可以看作反映像素光谱信息的光谱曲线。

图1 HSI的数据形式示意图

1.2 基于聚类的波段选择方法

考虑到波段之间的冗余性,基于聚类的波段选择方法需要首先确定一个相似性度量准则来衡量波段之间的相似性,然后,利用聚类算法将相似度较高的波段图像分为一组,在每一组中选择一个最有代表性的波段图像作为聚类中心,以选择出相似性较低的波段组合。其中,所使用的最经典的聚类算法便是K-means算法[21]。

K-means算法是一种无监督的聚类方法,其原理是,在样本总数为N的数据集X中随机选取K个样本点作为初始聚类中心,依据剩余N-K个样本到每个聚类中心的距离,将这N-K个样本点划分到最近的聚类中心所对应的类中。划分完成后,计算每一类样本的均值向量,判断是否需要重新确定聚类中心,重新把样本点分配到各个聚类中,通过迭代重新划分类别,直到类中心不再改变或达到最大迭代次数为止。

基于K-means聚类的波段选择方法通过聚类算法对高光谱遥感图像数据进行聚类分析,得到K个簇,然后从每个簇中选取簇中心波段,组成波段子集,将其作为输入特征用于遥感图像的分类与识别。假设已知一个波段集合X,即

X={xi|xi=xi1,xi2,…,xim;i=1,2,…,l}

(1)

式中：l为高光谱图像波段数量;xi=xi1,xi2,…,xim为第i个波段数据;xim表示第i个波段数据中m个像素的值。

设置初始的聚类中心波段为

C={ci|ci=ci1,ci2,…,cim;i=1,2,…,k}

(2)

式中：k为聚类数目;ci=ci1,ci2,…,cim表示第i个聚类中心波段数据中m个像素的值。

第i个波段xi与第j个聚类中心波段cj之间的欧式距离的计算表达式为

(3)

迭代过程中的聚类中心j波段数据cj的计算表达式为

(4)

式中：nj表示第j个聚类中心的波段数量;xj表示j波段相关数据。

1.3 马氏距离

马氏距离[19]由印度统计学家Mahalanobis提出。马氏距离表示服从某种分布并且其协方差矩阵为C的样本集X中的样本点x与y的差异程度,与欧氏距离不同的是,马氏距离考虑各特征之间的相关性,在高维空间中仍然具有较好的应用效果,适合应用于分类问题中。设样本集X中的元素均为n维向量,其均值向量为μ,协方差矩阵为C,则单个样本点x与均值的马氏距离可以表示为

(5)

样本集X中两个样本点x、y之间的马氏距离的计算表达式为

(6)

马氏距离与欧氏距离对比示意如图2所示。图中,黑点为属于样本M的一系列点,随机点A和点B相对于样本中心,即坐标原点O的直线距离d1和d2相等。考虑欧氏距离,A、B两点属于该样本集M的概率一样。但是,从整个样本分布来看,明显可以看出B点相对于A点更有可能是属于样本集M中的点。而在使用马氏距离进行计算的过程中,对协方差进行归一化处理,可以避免欧氏距离对于数据特征方差不同的影响,使其计算的距离结果更符合数据的分布特征及实际情况。

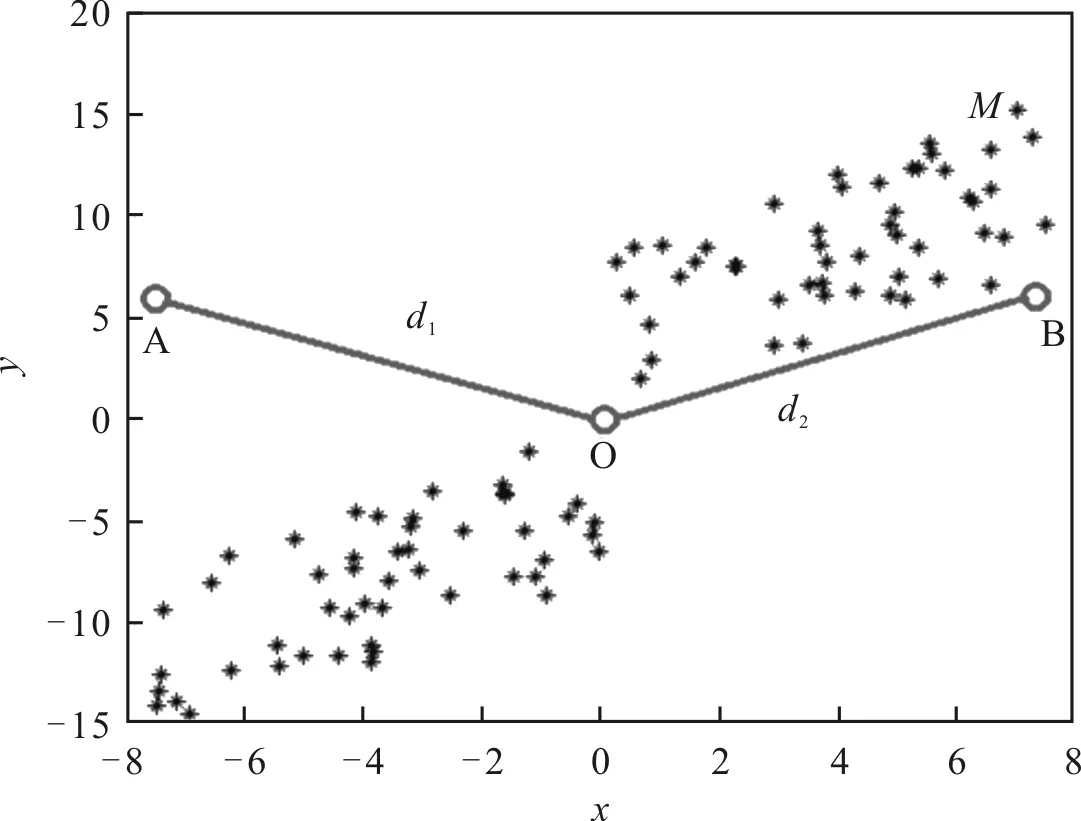
图2 马氏距离与欧氏距离对比示意

2 基于马氏距离聚类的波段选择方法

为了降低算法复杂度,提出的基于马氏距离聚类的波段选择方法的主要思路为：首先,根据要选择的波段数量对HSI数据进行粗子空间划分;其次,基于马氏距离聚类对HSI数据进行细子空间划分,相对于欧氏距离,马氏距离考虑特征之间的相关性,为此,利用马氏距离聚类得到的波段分组更符合高光谱图像波段的物理特性;最后,在每个波段组合中选取噪声最小的波段组成最终的波段子集。

2.1 粗子空间的划分

设X∈RW×H×L表示高光谱图像数据立方体,其中,L为总的波段数,W和H分别为每个波段的宽度和高度。由于连续波段之间的数据具有较高的冗余性,因此,在进行波段聚类之前根据选择的波段数量将HSI数据立方体分为有限的子立方体。将每个子立方体的波段数定义为

z=L/k

(7)

式中,k表示要选择的波段数量。经过粗子空间划分得到k个子立方体Pi,i∈[1,k]。

2.2 基于马氏距离聚类的细子空间划分

2.2.1 波段间马氏距离

将高光谱数据立方体X∈RW×H×L展开为N×L维的二维矩阵S。其中,N=W×H,Si中每一行元素表示第i个波段的所有像素点的信息,每一列元素表示第i个像素在不同波段下的响应值。高光谱图像波段i、j间的马氏距离可以表示为

(8)

式中,C表示高光谱图像整体数据的协方差矩阵。

2.2.2 基于马氏距离的聚类

设k个子立方体为初始的k组,将第c组的所有波段数据的平均值作为初始的聚类中心mc(c=1,2,…,k),聚类中心的计算表达式为

(9)

式中：i表示第c组数据中的所有波段的波段编号;nc表示第c组数据的波段个数。

根据HSI的特性,相邻组之间数据的相关性较高,因此,只需要对相邻组波段的分组情况进行调整。计算相邻两组的所有波段到这两组的聚类中心之间的马氏距离,其计算表达式为

(10)

式中：下标i表示波段编号;下标c表示组编号。

根据式(10),分别按照组别为(1,2)、(2,3)、…、(k-1,k)的顺序,将相邻两组中的波段归类到距离最短的聚类中心所在类中。重复上述过程,直到每一组的聚类中心不再发生改变时为止,得到最终的聚类结果。

2.3 波段子集的选取

经典的波段选择方法往往通过信息散度来选择代表波段,选出的波段不可避免地会存在噪声信息,从而无法获得较为可靠的结果,影响后续的数据分析[17],为此,选择每个组中噪声最小的波段作为代表波段。计算噪声的方法通常是将图像分为干净图像和噪声图像两个部分[12]。为了避免直接的图像分解,利用局部方差估计每个波段图像的噪声水平,然后,选择每个子立方体中噪声最小的波段图像作为所选波段,组成最终选择的波段子集,具体步骤如下。

首先,将每一个波段图像分割为大小为B×B像素的小块。对于无法完全分割的波段图像,删掉波段图像中最靠近边缘的行或者列,以便于将整个图像分割为相同大小的块,这样操作不会影响实验结果。

由于一些块具有相似的频谱特征,为了加快算法的处理速度,从原始的块中随机选择M个块,这种处理方式能够大大缩短处理时间。每个块的局部平均值M和局部方差V的计算表达式分别为

(11)

(12)

式中：B2为数据块中像素的数量;Si表示数据块中第i个像素的值。

然后,计算出每个波段图像中M个数据块的方差之后,根据小块的方差来估计图像的噪声。图像划分的小块中存在一部分同质块和一部分非同质块,同质块的方差较小,非同质块的方差较大,如果直接通过计算所有小块方差的平均值来处理这些结果,就会导致噪声的估计值不准确。针对该问题,采取将小块分组的策略,将每个图像的M个数据块,分为k组,将每个波段的M个数据块分别放到对应的组中,计算数据块数量最多的分组方差的平均值作为该波段图像的噪声估计值。

k的计算表达式为

(13)

式中：Vmax表示该波段图像的M块中方差的最大值;Vmin表示该波段图像的M块中方差的最小值;α为区分粒度。

2.4 基于马氏距离聚类的波段选择方法

对于一幅高光谱图像X∈RN×L,L表示波段个数,N表示单波段的像素个数,提出的基于马氏距离聚类的波段选择方法可分为以下几步。

第一步,确定选择的波段数k,将高光谱波段平均分为k组,经过粗子空间划分得到k个子立方体Pi,其中,i=1,2,…,k。

第二步,根据式(9),求出每一组所有波段数据的均值向量作为该组数据的聚类中心mc,其中,c=1,2,…,k。

第三步,根据式(10),计算相邻两组的所有波段到这两组的聚类中心之间的马氏距离,波段与哪个聚类中心之间的马氏距离越小,就分到对应的波段子集中。重复第二步和第三步的操作,直到每个波段组合的聚类中心不再发生变化,得到最终的聚类结果。

第四步,根据式(12),计算每个波段图像的噪声级Ni,其中i=1,2,…,L。选出每组波段中噪声级最小的波段,组成最终的波段子集。

第五步,将最终选出的波段子集分别利用SVM、KNN和ELM分类器进行地物分类,得出分类结果。

提出的BS-MDC方法流程图如图3所示。

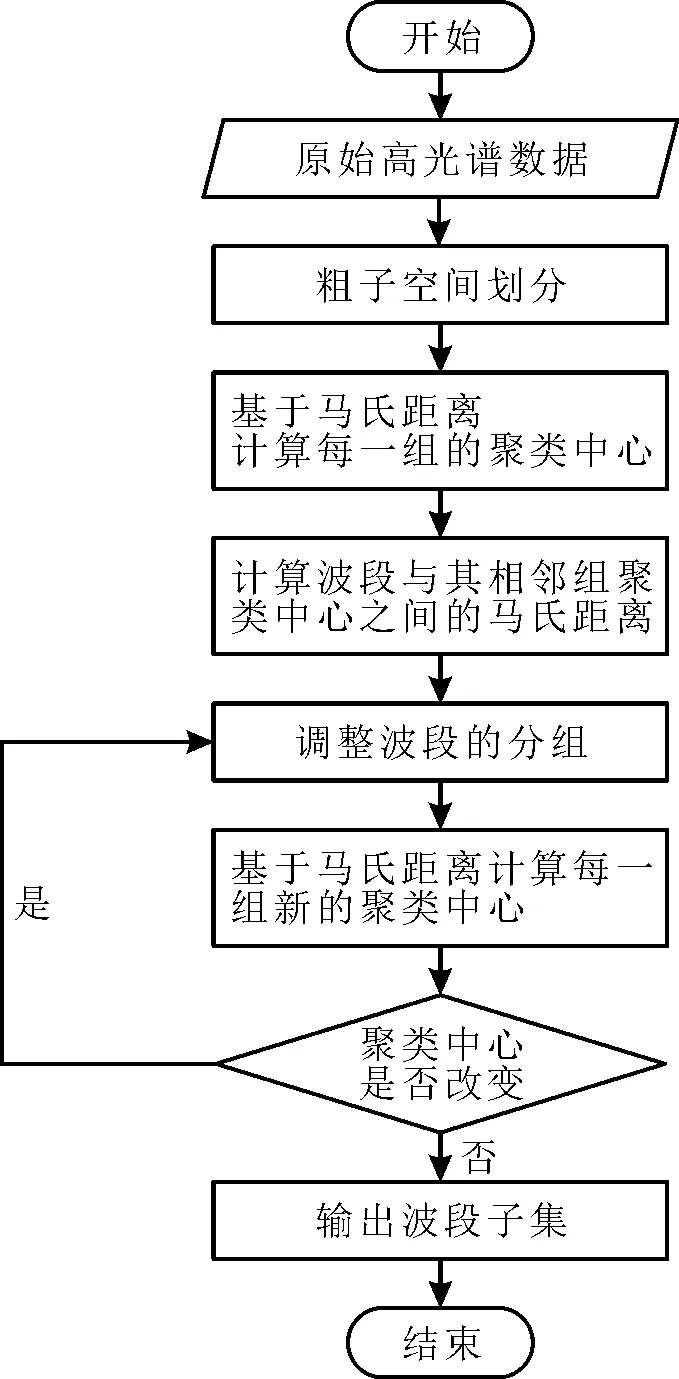
图3 BS-MDC方法流程图

3 仿真结果及分析

为了验证BS-MDC算法的有效性,采用Matlab R2018a软件进行仿真,并与MVPCA[13]、OPBS[15]、E-FDPC[17]和OCF[18]算法等几种经典的波段选择算法进行对比。

实验使用的计算机CPU版本为Intel(R)Core(TM) i5-7300HQ,操作系统为64位,主频2.50 GHz,内存容量为8.0 GB。

3.1 参数设置

BS-MDC算法的参数设置为,对每个波段图像进行分割的尺寸设置为3×3像素,随机选择的像素块数量M设置为200,区分粒度α的值设置为3,分别使用SVM、KNN和ELM等3个分类器进行分类。对于SVM、KNN和ELM这3个分类器,均选择最优的参数组合进行实验,以确保实验的准确性。选择多项式核作为SVM的核函数,SVM分类器中的惩罚系数C等参数使用Matlab中的libsvm工具包的fitcsvm进行自动超参数寻优;KNN分类器中的最近邻数字K通过交叉验证方法在[1,15]范围内以步长为2选取出最优的K值;ELM分类器随机生成输入权植w和输入阈值b;波段选择的个数为5～50。

4种对比算法中,OPBS算法、E-FDPC算法以及OCF算法均为无参数算法。文献[13]中MVPCA算法的发散阈值设置为1.5。4种对比算法所用到的分类器的KNN分类器中的最近邻数字K设置为3,SVM分类器的核函数采用线性核函数,使用Matlab中的libsvm工具包的fitcsvm进行自动超参数寻优确定SVM分类器的惩罚系数C。

3.2 数据集

主要采用高光谱遥感图像公开数据集印第安松(Indian Pines)和肯尼迪航天中心(Kennedy Space Center,KSC)进行实验。Indian Pines数据集由机载可见光/红外成像光谱仪(Airborne Visible Infrared Imaging Spectrometer,AVIRIS)高光谱仪在印第安纳州农业实验场采集,该数据集包含224个145×145像素的高光谱图像,其中包含16种地物类别,空间分辨率为20 m。去掉含噪声以及水汽影响的24个波段,其余200个波段作为用来实验分析的数据集。KSC数据集由AVIRIS高光谱仪在佛罗里达州肯尼迪航天中心采集,该数据集包含512×614像素的高光谱图像,其中包含13种地物类别,空间分辨率为18 m。去除水汽影响的波段后,保留176个波段作为用来实验分析的数据集。Indian Pines数据集包含的地物类型较多,数据中的混合像元较多,分类难度较大,更能检验出降维方法的优越性;KSC数据集受噪声污染较为严重,也为地物分类造成了很大的干扰,更能检验出降维方法的鲁棒性。

Indian Pines数据集和KSC数据集中的伪彩色图像以及真实分类图像示例分别如图4和图5所示。伪彩色图像可以直观地看出地面物体的地貌,真实分类图像则可以看出代表每种地物类型的颜色及位置。

图4 Indian Pines数据集图像示例

图5 KSC数据集图像示例

实验中,利用SVM、KNN和ELM等3个分类器进行高光谱分类。由于高光谱数据集的规模比较庞大,如果训练集占比过大则消耗资源多,训练时间也会过长,因此,仿真实验中选取总数据集的10%为训练集,剩下90%为测试集。

3.3 定量评价指标

高光谱图像降维的目的一般是为了能够更好地进行地物分类,采用高光谱图像分类常用的整体正确率(Overall Accuracy,OA)和卡帕(Kappa)系数这两个评价指标作为算法的评价指标[22]。OA为被正确分类的类别像元数与总的类别个数的比值,OA值能较好地表征分类精度,但是,对类别像元个数极度不平衡的多类地物来说,其值受到像元数据较多类别的影响较大。Kappa系数同样被常用于衡量分类精度,且适用于各类别样本数量不平衡的分类问题。因此,常用这两个评价指标来判断分类效果的优劣。OA和Kappa系数这两个指标的取值范围都在[0,1]之间,且数值越大越好,说明降维后的数据更有利于高光谱图像的地物分类。

3.4 仿真结果

使用所提BS-MDC算法对两个数据集进行波段选择,基于ELM、KNN和SVM 3个分类器对地物进行分类,选择不同波段数量得出的分类整体正确率实验结果如图6所示。从图6中可以看出,在Indian Pines数据集和KSC数据集两个数据集上,KNN、SVM和ELM等3种分类器的实验结果有一个共同特点,即KNN分类器的分类精度都是最低的。对于SVM分类器和ELM分类器,在选择波段较少的情况下,即低于20个波段时,利用ELM分类器对BS-MDC算法进行降维后的高光谱数据处理,得到的分类精度相对较高;当选择波段数量较多时,ELM分类器的分类精度比SVM的分类精度更低,由此可以得出结论,利用BS-MDC算法进行高光谱图像的波段选择,在选择较少波段的情况下,ELM的分类效果更好。

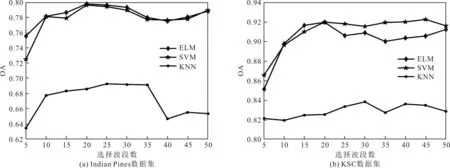
图6 3种分类器的分类整体正确率

使用所提BS-MDC算法、MVPCA算法、OPBS算法、E-FDPC算法和OCF算法等5种算法对Indian Pines和Kennedy Space Center两个高光谱数据集进行波段选择,由于对比算法中常用的分类器为SVM和KNN,因此,采用这两种分类器进行实验。当采用KNN和SVM两种分类器进行分类时,5种算法分别对Indian Pines数据集和Kennedy Space Center数据集分类的分类整体正确率实验结果分别如图7和图8所示,图中,Baseline为用原始图像作为分类器的输入时得到的整体准确率。

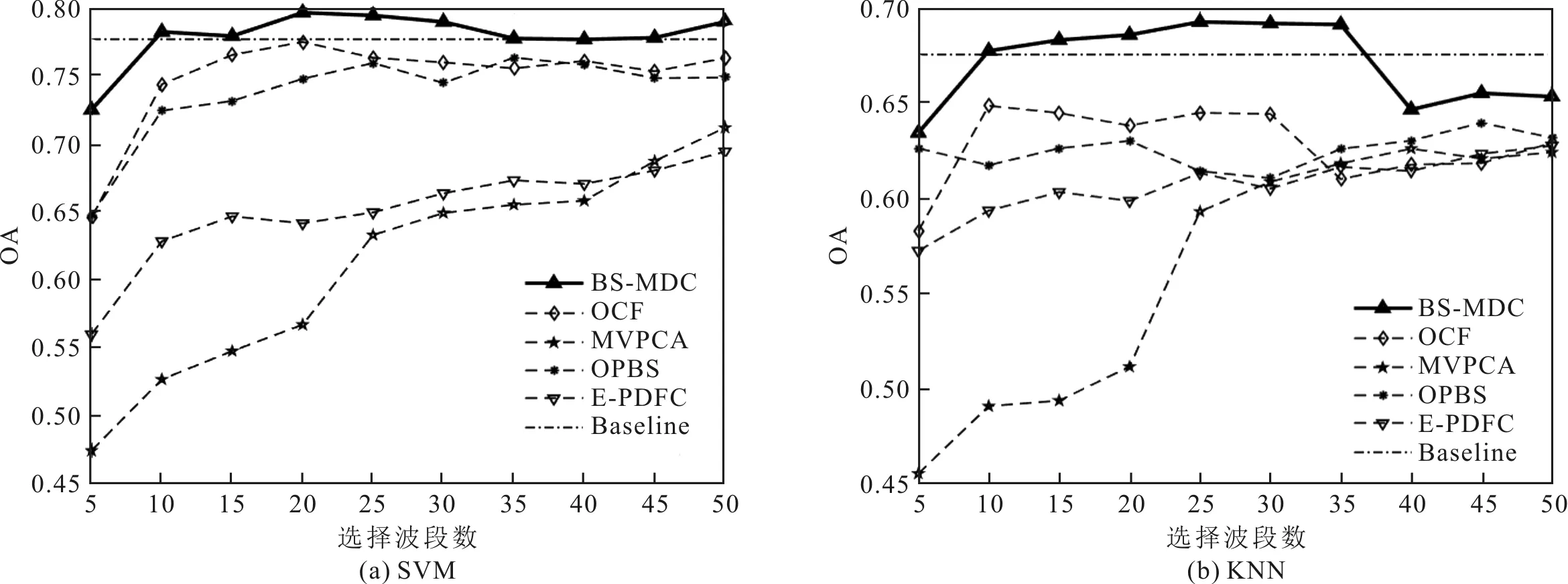
图7 Indian Pines数据集的分类整体正确率

图8 KSC数据集的分类整体正确率

从图7可以看出,针对Indian Pines数据集,当采用KNN和SVM两种分类器进行分类时,在5种波段选择算法的分类整体正确率实验结果中,所提BS-MDC算法的分类整体正确率明显优于OCF、MVPCA、OPBS和E-FDPC这4种波段选择方法。使用SVM和KNN分类器时,在选择波段较少的条件下,BS-MDC算法即达到了较高的整体正确率。尽管当使用KNN分类器进行分类时,BS-MDC算法在选择39个波段时,OA虽有一个大幅度的降低,但是,也优于其他4种算法的分类整体正确率。

从图8可以看出,针对KSC数据集,当采用KNN和SVM两种分类器进行分类时,在5种波段选择算法的分类整体正确率实验结果中,所提BS-MDC算法的分类整体正确率较优。其中,当利用KNN分类器进行分类时,BS-MDC算法的精度曲线明显优于OCF、MVPCA、OPBS和E-FDPC算法这4种波段选择算法,在精度方面具有明显的优势,同时,OA值稳定且较高。当利用SVM分类器进行分类时,虽然所提BS-MDC算法相对于OCF算法具有的优势较小,但是,精确度也略高于OCF算法。由于KSC数据集被盐噪声严重污染,因此,在KSC数据集上的实验结果从另一方面也表明了所提BS-MDC算法在噪声较强的情况下具有较好的鲁棒性。

从图7和图8的实验结果还可以看出,5种分类算法对Indian Pines数据集和Kennedy Space Center数据集两个数据集的分类结果中,MVPCA算法的分类整体正确率表现最差,这是因为,一方面,MVPCA算法只是利用方差排序,未考虑波段之间的相关性;另一方面,基于方差的MVPCA算法对噪声相对比较敏感,所以表现较差。而所提BS-MDC算法在地物类型较多且复杂的Indian Pines数据集以及受噪声污染较为严重的KSC数据集上的表现明显较好,体现出BS-MDC算法在处理复杂且噪声污染严重的高光谱图像时仍具优势,比其他的算法更有效,对不同分类器的鲁棒性更强。

使用5种不同算法,对Indian Pines数据集和KSC数据集两个数据集进行波段选择,选择5～50个波段,使用KNN和SVM两种分类器,5种算法分类性能对比结果如表1所示。其中,使用地物分类的整体正确率的平均值 (Average Overall Accuracy,AOA) 以及Kappa系数的平均值(Average Kappa,AK)两个精度指标,对5种算法的性能进行对比。

表1 5种算法分类性能对比

由表1可以看出,对于Indian Pines数据集和KSC数据集两个高光谱数据集,所提BS-MDC算法对高光谱图像降维后利用KNN和SVM进行分类的整体分类精度AOA以及平均Kappa系数AK的值均高于其他4种波段选择方法,说明所提BS-MDC方法选出的波段更有利于进一步地物分类。

为了进一步验证5种不同波段选择算法的性能,5种算法均使用SVM分类器,在Indian Pines数据集和KSC数据集两个数据集上选择同样波段数目(以20个波段为例),仿真5种不同算法对地物的分类准确率,5种算法对Indian Pines数据集和KSC数据集的分类效果分别如图9和图10所示。Indian Pines数据集和KSC数据集两种数据集中不同地物类型的分类整体正确率分别如图11和图12所示。

图9 Indian Pines数据集分类效果

图10 KSC数据集分类效果

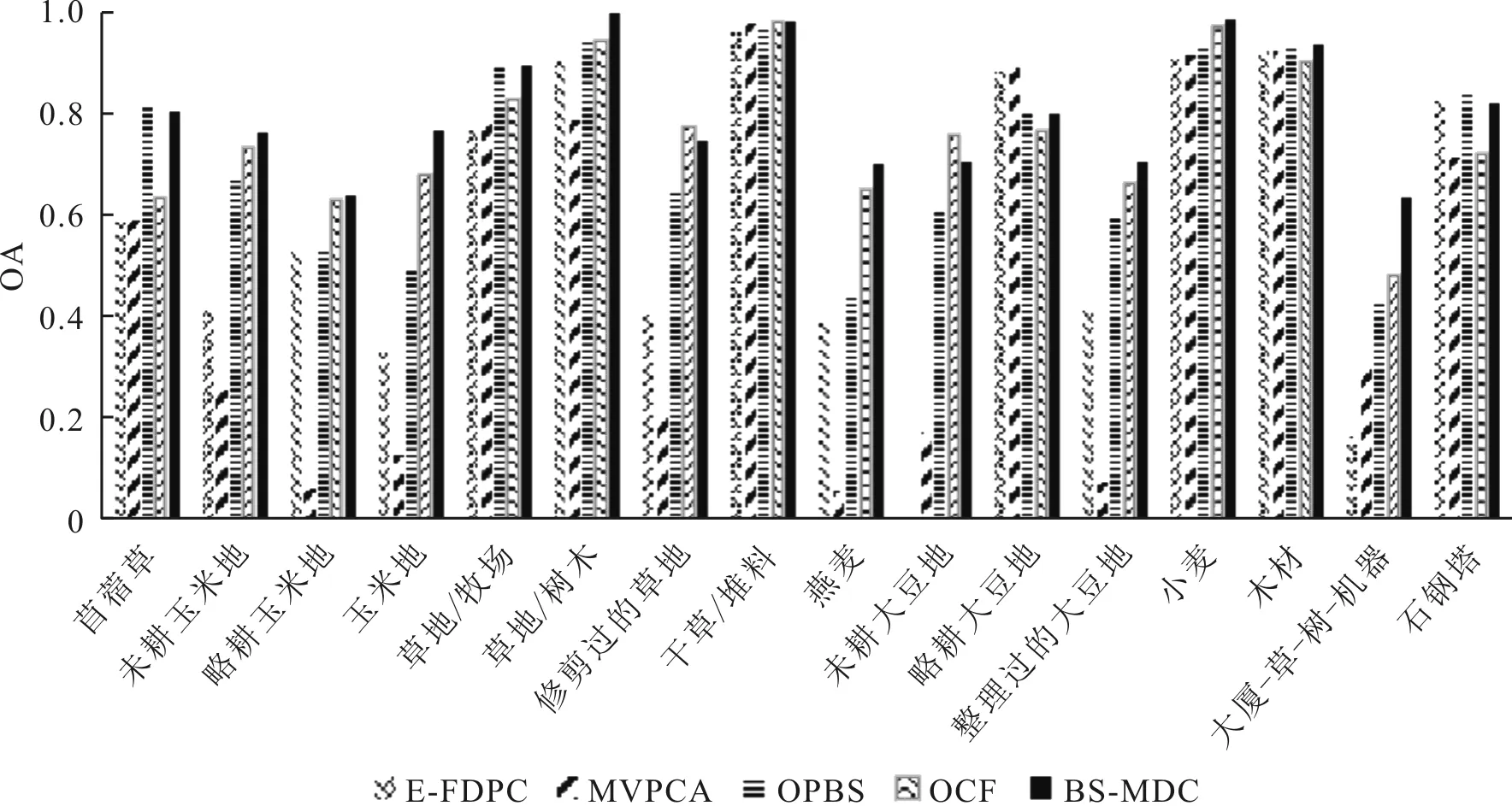
图11 Indian Pines数据集各地物分类精度

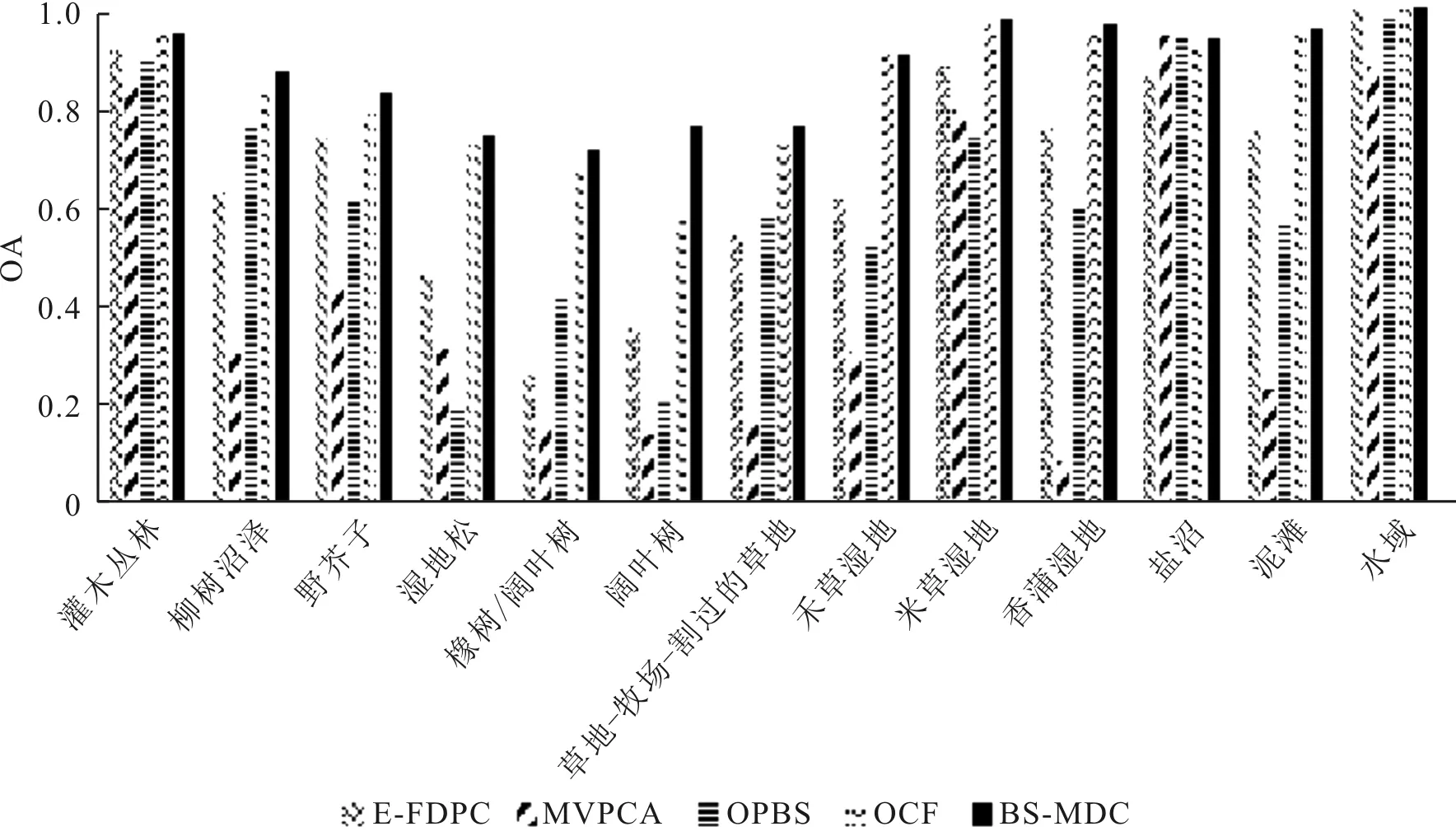
图12 KSC数据集各地物分类精度

从图9和图10中可以看出,在两个不同数据集的不同地物类型的分类中,BS-MDC算法得到的波段组合在SVM分类中表现最好,分类结果图中的椒盐噪声最少,且错分现象不严重。而在4种对比算法中,MVPCA算法得到的分类结果图中的椒盐噪声最多,错分现象最严重。从图11和图12中可以看出,BS-MDC算法在Indian Pines数据集和KSC数据集两种数据集中大多数地物类型上的分类整体正确率最高。

4 结语

为了减少高光谱图像在对其波段进行分组时受到数据分布特征的影响,提出了一种基于马氏距离聚类的高光谱图像波段选择方法。该方法在波段子空间划分的基础上进行聚类,有效减少了算法的运行时间,另外,利用马氏距离作为波段间相似度的度量准则,以选择出相似度低的波段组合。从两个真实数据集的实验结果可以看出,BS-MDC算法在不同波段数的情况下都有较好的分类性能,比其他算法有明显的优势,对地物类别较为复杂的Indian Pines数据集和受噪声污染较为严重的KSC数据集都有较好的表现,分类精度较高,且具有较好的鲁棒性。