室性并行心律合并二、三联律的散点图特点及数学原理
申继红 景永明 李世锋
室性并行心律的心电图特征[1]如下: ①联律间期不固定;②各室性异位搏动周期之间存在一个最大公约数;③常出现室性融合波。 随着散点图技术的发展,越来越多的室性并行心律被识别并诊断。 景永明等[2]采用几何画板建立了并行心律的Lorenz 散点图与差值散点图模型,但这些模型并未展示并行心律合并二、三联律时的散点图特点。 向晋涛等[3]总结出了窦性心律(简称窦律)合并室性并行心律的大数据Lorenz 散点图呈“△”形组合图形,但并未总结差值散点图的特点。
笔者在上述研究的基础上,从临床遇到的室性并行心律散点图中选取3 例各具特点的病例,进一步深入总结室性并行心律合并二、三联律时的Lorenz散点图及差值散点图特点,再利用数学原理进行分析,计算相关点集的直线方程,并利用几何画板的动态作图功能和轨迹跟踪功能制作其数学模型。
1 散点图分析
1.1 病例1
图1 来自病例1,图1A、1B 分别是24 h 动态心电图记录到的1 例典型室性并行心律的Lorenz 散点图与差值散点图。 Lorenz 散点图(图1A)特点:窦律点集(NNN)呈棒球拍样,分布于等速线上,室性早搏点集(NVN)沿垂直于等速线的方向向等速线延伸,主轴斜率为-1,早搏前点集(NNV)和早搏后点集(VNN)分别沿垂直及水平方向向等速线延伸,总体呈斜倒的“Y”字形分布。 差值散点图(图1B)特征: 窦律点集(NNNN)位于坐标原点,相当于普通室性早 搏 的 起 点(NNNV)、 始 点(NNVN)、 终 点(NVNN)、止点(VNNN)呈四分布图形,在各自的方位向坐标原点的窦律点集延伸,其中NNNV 点集位于y轴负侧,VNNN 点集位于x轴负侧,两个点集关于y=x线对称分布;NNVN 点集位于第二象限,主轴斜率为-2,NVNN 点集位于第四象限,主轴斜率为-1/2,两个点集也关于y=x线对称分布。 上述特点与景永明等[2]制作的心电散点图数学模型完全相符,体现出室性并行心律联律间期不固定、代偿间歇完全的电生理特征。
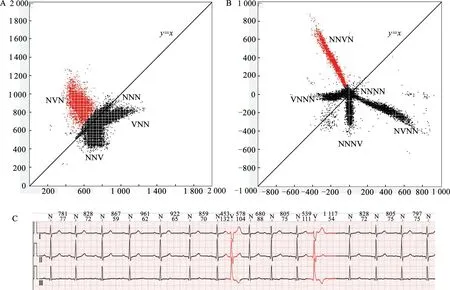
图1 病例1 的24 h Lorenz 散点图、差值散点图及心电图片段
1.2 病例2
图2 来自病例2,图2A -2D 是24 h 动态心电图记录到的1 例典型室性并行心律合并大量二联律的Lorenz 散点图与差值散点图。 与病例1 相比,病例2 的24 h Lorenz 散点图(图2A,扫描OSID 码可查阅彩图) 的不同点在于:绿色室性早搏点集(NVN)呈“△”形,位于等速线以上的短-长周期区,早搏前点集(NNV)、早搏后点集(VNN)及二联律点集(VNV)重叠于等速线以下的长-短周期区而不易分辨;在1 h Lorenz 散点图(图2B)中,各点集呈现出与病例1 相同的斜倒的“Y”字形分布,室性早搏点集(NVN)和二联律点集(VNV)均垂直于等速线,主轴斜率均为-1,并在等速线附近呈上下前后错开。
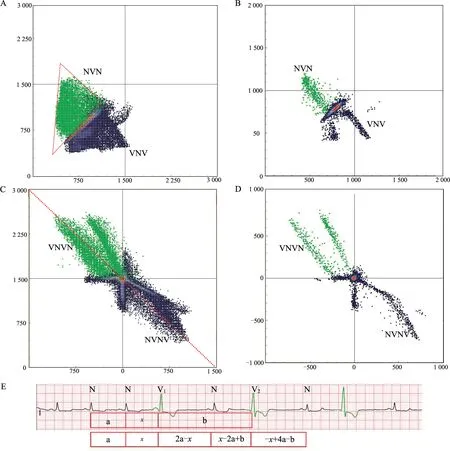
图2 病例2 的24 h 及1 h Lorenz 散点图、差值散点图及心电图片段
与病例1 相比,病例2 的24 h 差值散点图的不同点(图2C)在于:在第二、四象限角平分线可见对称分布的大量二联律相关点集(VNVN、NVNV),这两种点集较为分散,呈现出一定宽度。 而在1 h 差值散点图(图2D)中,VNVN、NVNV 点集并不位于第二、四象限角平分线上,而是分别向左、向右偏离原点一定距离。
以下通过计算室性早搏点集(NVN)和二联律点集(VNV)的直线方程,解释1 h Lorenz 散点图(图2B)中两个点集均垂直于等速线,并在等速线附近呈上下前后错开的原因。 如图2E 所示,室性并行心律的联律间期NV 不固定,设为变量x,基础窦律周期NN 相对恒定,设为定量a,室性搏动之间的周期VV 间期也相对恒定,设为定量b,那么,可以计算出各RR 间期值,进而得出两个点集的横、纵坐标。二联律点集V1NV2的横坐标x′=V1N=2a -x,纵坐标y′=NV2=x-2a+b。 两个坐标中均含有变量x,计算消除后,可得出直线方程y′ = -x′ +b。 同理,室性早搏点集NV1N 的横坐标x′=NV1=x,纵坐标y′=V1N=2a-x。 两个坐标中均含有变量x,计算消除后,可得出直线方程y′ = -x′ +2a。 两个点集的直线方程中,变量系数均为-1,即主轴斜率均为-1,所以两个点集均垂直于等速线分布。 V1NV2点集的直线方程为y′ = -x′ + b,当x′ =0 时,y′ = b;当y′=0 时,x′ = b,即该直线方程与x、y轴的交点均为b,由室性并行心律的固有周期VV 间期决定;NV1N 点集的直线方程为y′ = -x′ +2a,当x′ =0时,y′=2a;当y′=0 时,x′=2a,即该直线方程与x、y轴的交点均为2a,由窦性节律周期NN 间期决定。所以,两个点集前后错开,当VV 间期恰好等于2 倍NN 间期时,两个点集可能存在共线这一极限状态。
采用同样的方法,可以计算出1 h 差值散点图(图2D)中二联律相关点集NV1NV2和V1NV2N 的直线方程(表1)。 NV1NV2点集的直线方程为y′ =-x′-2a+b,即该点集的主轴斜率为-1,当x′ =0时,y′=b-2a;当y′=0 时,x′=b -2a;同理,V1NV2N点集的直线方程为y′= -x′+2a -b,即该点集主轴斜率为-1,当x′ =0 时,y′ =2a - b;当y′ =0 时,x′=2a-b。 因为两个直线方程都有截距,所以就能解释为何二联律相关点集并不位于第二、四象限角平分线上,而是分别向左、向右在x轴上偏离原点一定距离(偏移的距离等于VV 间期与2 倍NN 间期之差);当VV 间期恰好等于2 倍NN 间期时,直线方程的截距为0,两个点集可能出现位于第二、四象限角平分线这一极限状态。

表1 室性并行心律合并二、三联律相关点集的直线方程及斜率
1.3 病例3
图3 来自病例3,图3A、3B 分别是24 h 动态心电图记录到的1 例典型室性并行心律合并大量二、三联律的Lorenz 散点图与差值散点图。 与病例2相比,病例3 的24 h Lorenz 散点图(图3A)的不同点在于:室性早搏点集(NVN)呈“△”形,位于等速线以上的短-长周期区,但“△”形靠近原点的顶端未充满且绿色点集内部有少量点集缺失。 与病例2相比,病例3 的24 h 差值散点图(图3B)的不同点在于:在第三象限可见偏离角平分线分布的三联律点集VNNV,主轴斜率为1。
以下从数学角度,解释差值散点图中三联律点集呈现上述特点的原因。 如图3C 所示,设室性并行心律的联律间期为变量x,基础窦律周期为定量a,室性搏动周期为定量b,那么,可以计算出各RR 间期值,进而计算出差值散点图中三联律特征性点集V1NNV2的横、纵坐标。 V1NNV2的直线方程为y′=x′-3a+b,即该点集的主轴斜率为1,当x′=0 时,y′ = -3a + b;当y′ =0 时,x′ =3a - b。由于直线方程中截距的存在,且b >3a,因此,就能解释为何三联律特征性点集并不位于第三象限角平分线上,而是向左在x轴上偏离原点一定距离(偏移的距离等于VV 间期与3 倍NN 间期之差);当VV 间期恰好等于3 倍NN 间期时,直线方程的截距为0,可能出现位于第三象限角平分线这一极限状态。
2 数学模型制作
利用几何画板软件制作数学模型的过程如下:
第一步,建立平面直角坐标系,在y=x线上构造线段,并在线段上取一点NNN 用来控制窦律周期。 经NNN 点作y=x线的垂线,并取点NV1N 用来控制早搏点集,度量NNN 点的横坐标NN,度量NV1N 点的横坐标NV1及纵坐标V1N。 另在x轴构造线段OD,用来控制室性搏动间期V1V2并度量其长度。
第二步,计算各RR 间期的数值(NN、NV1、V1N、V1V2、NV2、V2N)、绘制相关点并予以追踪(NNN、NV1N、NNV1、V1NN、NV2N、V1NV2)。 拖动NV1N 点形成Lorenz 散点图(图4a)。
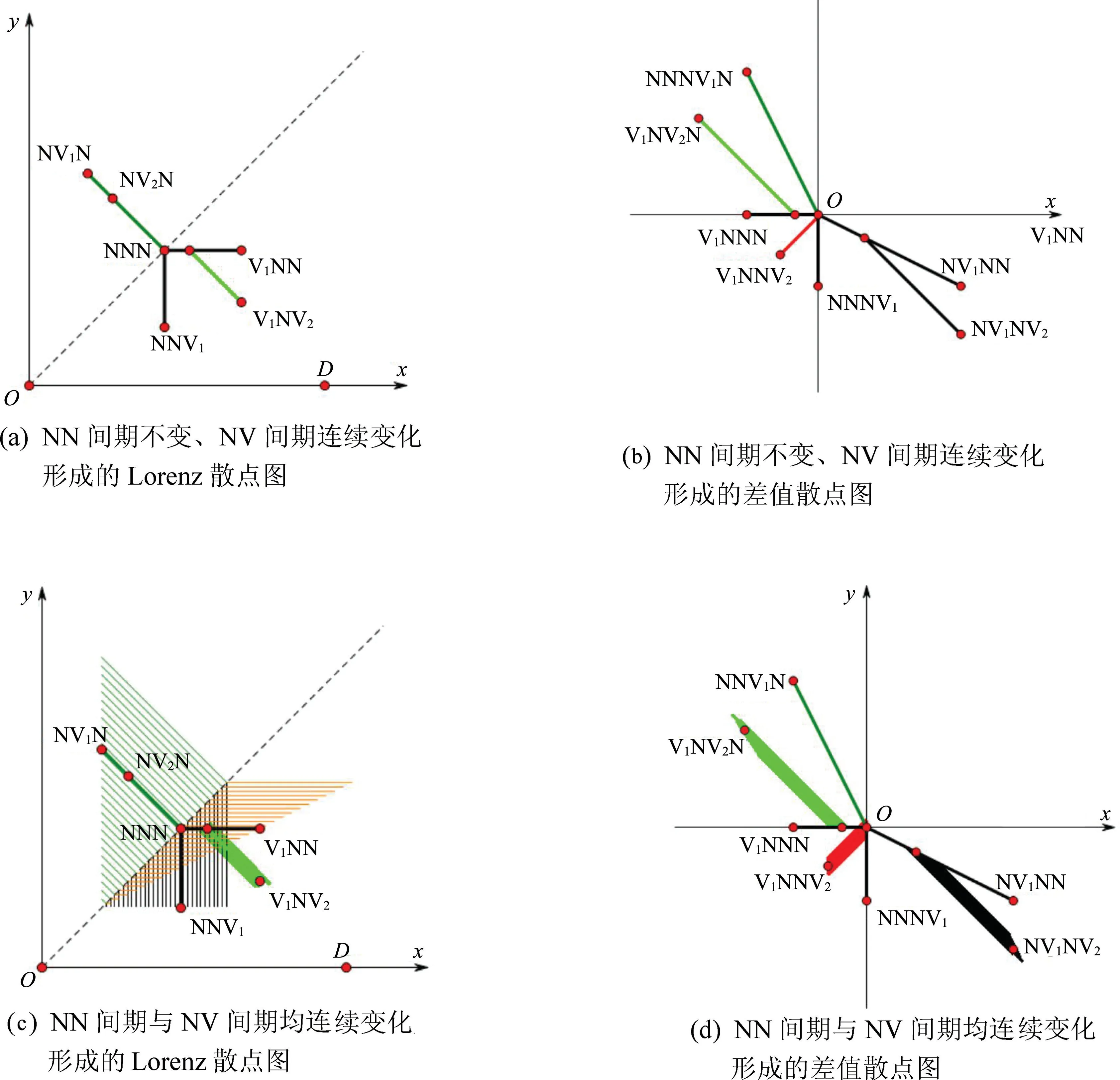
图4 利用几何画板制作的室性并行心律合并二、三联律的Lorenz 散点图与差值散点图数学模型
第三步,另建立平面直角坐标系用来绘制差值散点图,利用向量平移法[4]将Lorenz 散点图中的相关点集平移到差值散点图坐标系中(如NNN 指向NNV1,形成NNNV1),依次制作NNNV1点、NNV1N点、NV1NN 点、V1NNN 点、V1NV2N 点、NV1NV2点、V1NNV2点并进行追踪。 拖动NV1N 点形成差值散点图(图4b)。
第四步,构造图4a 中的4 条线段关于NNN 点集的 轨 迹, 并 追 踪 V1NV2点、 V1NV2N 点、NV1NV2点、V1NNV2点所在轨迹的线段,拖动NNN点并改变线段OD的长度,可得到相应的Lorenz 散点图及差值散点图图形(图4c、4d)。
3 讨论
普通室性早搏的联律间期相对固定、代偿间歇完全,而室性并行心律尽管代偿间歇完全,但联律间期不固定,因此,二者的Lorenz 散点图各有特点[5],差值散点图却有很多相似之处。 在Lorenz 散点图中,普通室性早搏的NVN 点集垂直于x轴分布,室性并行心律的NVN 点集垂直于等速线分布。在差值散点图中,两者的起(NNNV)、始(NNVN)、终(NVNN)、止(VNNN)四个点集的分布位置及斜率均相同,但因为室性并行心律的联律间期不固定,理论上NV 可以在原点及NN 间期之间分布,相邻RR 间期的差值,即(NV - NN)、(VN - NV)、(NN-VN)理论上也可以在原点及NN 间期之间分布,所以相关的起、始、终、止四个点集可以延伸到原点处的NNNN 点集。 两者的二联律点集(VNVN、NVNV)相比,普通室性早搏沿第二、四象限角平分线分布;室性并行心律在第二、四象限角平分线基础上向左、向右偏移原点一定距离(VV 间期与2 倍NN 间期之差),且点集更为分散,呈现出一定的宽度。 两者的三联律点集(VNNV)相比,普通室性早搏沿第三象限角平分线分布;室性并行心律在第三象限角平分线基础上向左偏离原点一定距离(VV间期与3 倍NN 间期的差值)。
室性并行心律在Lorenz 散点图中总体呈斜倒的“Y”字形分布,与文献[6 -7]的报道相符。 向晋涛等[3]列举了3 例典型的室性并行心律患者,其24 h Lorenz 散点图均呈“△”形组合,逆向观察任意1 h Lorenz 散点图,发现绝大多数呈倒“Y”字图形,亦有少数呈“△”形组合图形,但其散点分布较稀疏。 笔者观察到的Lorenz 散点图特点与上述报道一致,尤其是病例2 中24 h Lorenz 散点图与1 h Lorenz 散点图的对比很明显。 笔者认为,并行心律存在保护性传入阻滞及间歇性传出阻滞,其电生理机制决定了散点图特点。 在NN 间期不变的情况下,NV 间期与VN 间期连续性变化,形成了Lorenz散点图中特征性的倒“Y”字形(图4a)。 如果改变NN 间期,则特征性的倒“Y”字形会上下移动,其轨迹形成由三个不同的“△” 形组合而成的图形(图4c)。 也就是说,“△”形组合图形是由不同高度的倒“Y”字形累积和叠加而成,其中,NNV、NVN点集形成的轨迹为直角三角形,而VNN 点集形成的轨迹为钝角三角形,VNV 点集形成的轨迹是垂直于等速线的较宽条带。 当短时间内NN 间期与NV 间期变化均较大时,1 h Lorenz 散点图也可呈“△”形组合图形的特点。 病例3 中,“△”形靠近原点的顶端未充满,而使NVN 点集呈近似直角梯形样的分布,主要受全程窦律频率中最快心率的控制:当心率增快时,可能存在间歇性传出阻滞。而“△”形内部有少量点集缺失,提示窦律周期与联律间期并非完全呈连续、均匀变化,可能存在某些心率带的缺失,进而导致部分倒“Y”字形点集的缺失(也可能与相应频率带易发生传出阻滞有关)。 与二、三联律相比,室性并行心律VV 间期相对固定,当NN 间期较短(窦律频率较快)时,容易出现三联律;当NN 间期较长(窦律频率较慢)时,容易出现二联律。 无论窦律频率的变化多大,室性并行心律在差值散点图中均维持相对稳定(如图4b、4d)。
当室性并行心律合并二、三联律时,可使Lorenz散点图与差值散点图呈现更加复杂的特点。 如果能够总结这些特点,并利用数学原理找出散点图中隐藏的线性关系,将各点集用直线方程来解析,则有利于我们更加透彻地理解散点图中各点集的形成原理,进而利用几何画板制作数学模型,为临床快速准确诊断提供可靠依据。

