一道2021 年全国高中数学联赛试题的探究与变式

中国人民大学附属中学丰台学校(100074) 王宠

北京市第十二中学(100071) 刘刚

1.试题与解答

题目(2021 年全国高中数学联赛一试A1 卷第11 题)如图1 所示,在平面直角坐标系中,椭圆Γ:+y2=1的左、右焦点分别为F1,F2,设P是第一象限内Γ 上一点,PF1,PF2的延长线分别交Γ 于点Q1,Q2.设r1,r2分别为∆PF1Q2,∆PF2Q1的内切圆半径.求r1−r2的最大值.

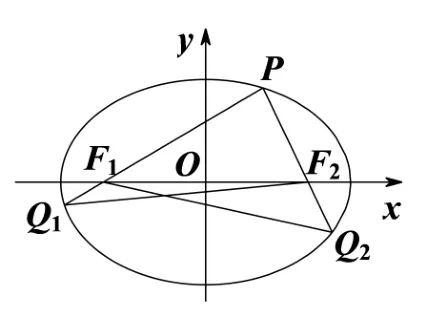
图1

试题考查了椭圆的定义、标准方程、几何性质、直线与椭圆的位置关系以及最值问题,考查了逻辑推理、直观想象、数学运算等核心素养,检验了学生分析问题与解决问题的能力.试题构思巧妙,解法多样,体现了在知识交汇处命题的特点.

解法1设P(x0,y0),Q1(x1,y1),Q2(x2,y2),由条件知F1(−1,0),F2(1,0)且x0,y0>0,y1<0,y2<0.由椭圆定义得

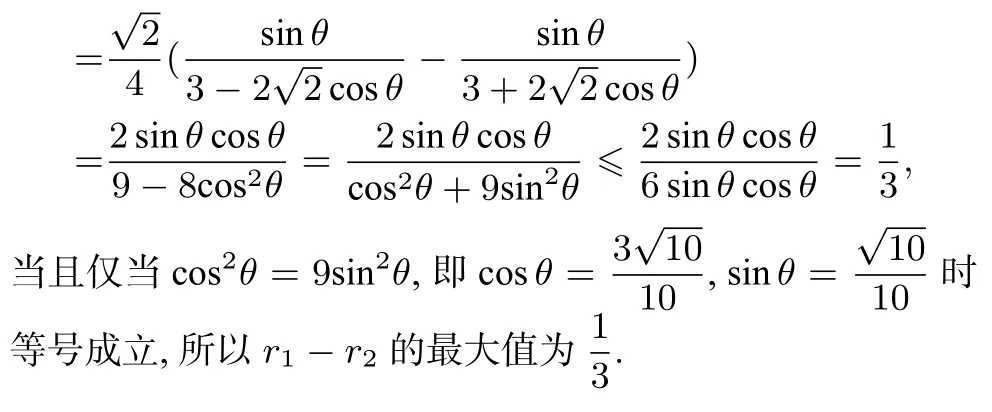
点评解法2 先借助椭圆的参数方程表示出点P,Q1,Q2的坐标,然后得到r1−r2,接下来利用向量共线定理、三角恒等变换等知识建立参数间的等式关系,最后利用均值不等式求得最值,体现了参数法和三角函数相关知识的应用,有利于培养学生的创新性.

2.推广探究

将试题一般化,得到:

3.变式

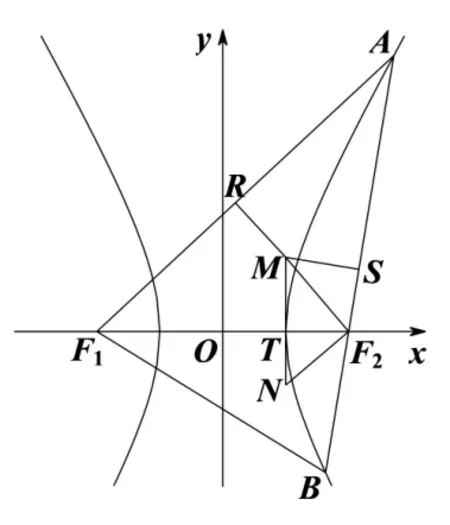
图2

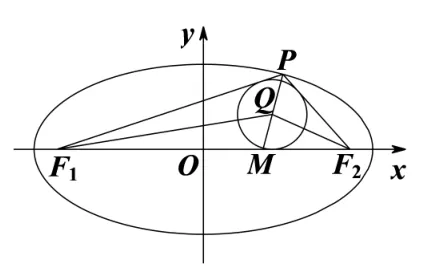
图3