约束条件下的柯西不等式:几何的视角

深圳市龙华区教育科学研究院附属外国语学校(518109) 钟文体

一、命题简证

二、几何背景

几何形式如图1,已知点O是平面π上的定点,点A为另一定点(平面内或平面外),点M在平面π上运动,求线段OA在直线OM上的投影的最大值.

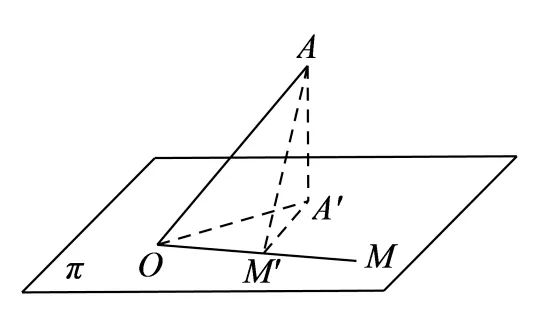
图1

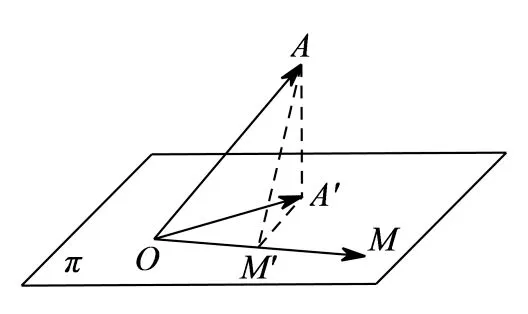
图2

若点A在平面π内,则当点M在直线OA上时,投影最大,最大值为线段OA的长度.以下考虑点A在平面π外的情形.如图1,作AA′⊥平面π,垂足为A′.作AM′⊥OM,垂足为M′.连接A′,M′,那么,∆OAA′,∆OAM′,∆AA′M′都为直角三角形.因此,

OM′2=OA2−AM′2=OA2−(AA′2+A′M′2)

=(OA2−AA′2)−A′M′2=OA′2−A′M′2≤OA′2,

(也可以通过证明OM′⊥A′M′来说明|OM′|≤|OA′|)于是,当点M′与点A′重合,即当点M在直线OA′上时,线段OA在直线OM上的投影取最大值,最大值即为线段OA在平面π上的投影的长度.

三、推广