回顾与沟通，促进模型构建

杨建明

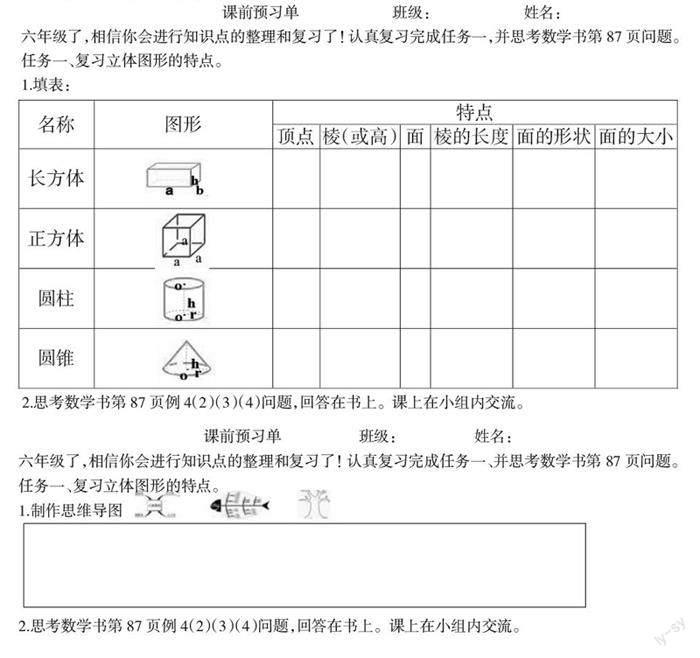
教学内容：数学人教版六年级下册第六单元P87例4、例5。

教学过程：

一、导入新课，揭示课题

1.（几何画板演示立体图形的生成过程）师：仔细观察，你发现了什么？你能用几个字总结一下吗？引导：刚才我们看到的过程其实可以用12个字来概括：点动成线、线动成面、面动成体。

2.揭示课题。师：点、线、面是立体图形的基本元素，这节课我们一起来进行立体图形的整理和复习。（板书课题：立体图形的整理和复习）

设计意图：追本溯源，立体图形其实是平面图形的累加而成，点线面是立体图形的基本元素。激活学生已有的知识经验，为立体图形的特征与模型构建提供载体。

二、操作探究，构建模型

活动一：自主整理，知识建构

1.师：回想一下，在小学阶段，我们都学过哪些立体图形？关于立体图形你知道些什么？请大家拿出任务单，对照修改订正。时间3分钟）

2.同学们，在预习整理的过程中，你有什么疑问吗？

思考：①长方体和正方体有什么相同点和不同点？

②圆柱和圆锥有什么相同点和不同点？

学生汇报交流。

3.游戏：我说你猜。（袋子里准备不同立体图形）

师：看来大家对立体图形的特征掌握得不错！下面老师来检测一下。随机请学生从袋子里摸图形，并向其他同学介绍摸到的感觉，全班同学猜是什么？

设计意图：一堂单纯的复习课很容易变得枯燥乏味，利用游戏激发兴趣，不仅能强化立体图形的特征辨识，有利于学生头脑中建立立体图形的空间模型，而且通过学生自主整理，师生交流、生生交流，将知识系统化，完善图形的模型建构。

活动二：操作想象，建构模型

师：图形与几何的学习，想象力非常重要！

1.（出示一张长方形纸）看到这张长方形纸你想到了哪种立体图形？

预设1：以边为轴旋转——圆柱。（师根据学生回答画出来）随机提问：有几种旋转方法？你能算出它的体积吗？（板书：V=Sh）

预设2：围起来，得到圆柱的侧面。随机提问：有几种围法？你能说说它的表面积怎么算吗？（板书：S表=S侧+S底×2）

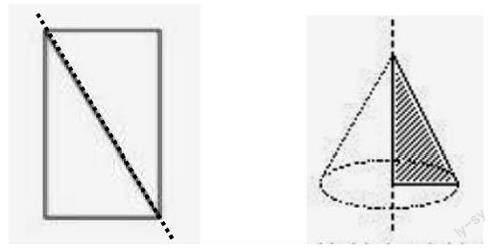
2.（出示这张长方形纸）再问：看到这张长方形纸你想到圆锥吗？（提示：先沿对角剪，再旋转——圆锥）

追问：这个圆锥与刚才的圆柱有什么关系？怎样求出圆锥的体积？（随机板书：等底等高，V=１/3Sh）

3.师：同学们，一张小小的长方形纸咱们想到了许多，看来想象确实重要啊！请大家想想，如果把这个圆柱切一切、拼一拼，你想到了什么？

预设：长方体。（出示拼成的长方体）谁来说一说，这个长方体与圆柱有什么关系？

4.师：同学们，如果把长方体的长、宽、高都缩减为同样长的线段，得到一个什么图形？（正方體）随机板书：特殊的长方体。你能说说它的公式吗？

设计意图：在数学建模教学中，让学生经历模型的诞生过程，在动手操作与汇报交流中让学生沟通圆柱与长方体、正方体的联系，体会转化的数学思想。不仅有助于培养学生的创新意识，还有助于数学思想方法和解决问题策略的学习。

活动三：建立联系，拓展模型

1.（还是刚才这张长方形纸）你能通过折一折，得到长方体或正方体吗？（引导对折2次，围成一个长方体或正方体）学生动手试一试。

提问：这张长方形的纸围成了长方体的什么面？（侧面）你能求出它的侧面积吗？（引导：底面周长×高）

2.观察发现一：长方体S侧=2ah+2bh、正方体S侧=4a2、圆柱体S侧=ch。无论长方体、正方体或圆柱体的侧面积，都可以用：底面周长×高。

3.观察发现二：三种立体图形的体积公式，无论长方体、正方体或圆柱体的体积，都可以用：底面积×高。

4.补充：认识直柱体及其特征。

（1）怎样求出下图物体的体积呢？（师演示一个一个累加）师：你想到了什么方法？（2）介绍直柱体。学生辨别生活中的直柱体并说说可以怎样计算它们的体积？

设计意图：生活原型是数学建模的逻辑起点。在数学建模过程中，教师要依据数学知识的学科特质以及学生的年龄、心理特征，引领学生将生活问题抽象成数学问题，将学生实际生活中的素材引入课堂，让学生运用“数学的眼光”去打量，用“数学的大脑”去考量，用“数学的语言”去描述。当认识了直柱体的特征以后，学生不难发现：直柱体的体积其实就是每层数的累加。利用这一模型，就很容易帮助学生理解统一公式了。

三、解释运用，巩固提升

1.选择题：

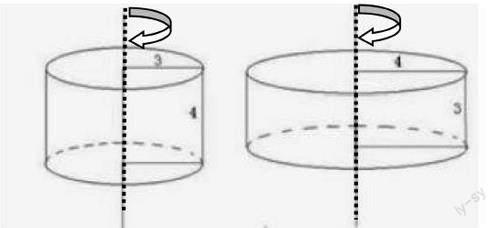
（1）小红做了一个圆柱和几个圆锥（如下图，单位：cm），在圆柱中装有水，将圆柱中的水倒入第（  ）号圆锥中，正好倒满。

（2）下面（  ）图形是圆柱的展开图（单位：cm）。

2.判断题：

（1）把圆锥的侧面展开，得到的是一个三角形。（  ）

（2）把一段圆柱形木材削成一个最大的圆锥，削去的部分是原来的。（  ）

（3）圆柱的底面半径扩大为原来的2倍，高不变，它的体积也扩大为原来的2倍。（  ）

（4）圆锥的体积等于圆柱体积的。（  ）

（5）等底等体积情况下，圆锥的高是圆柱高的3倍。（  ）

3.解决问题：一个密封的瓶子里装着一些水（如右图所示），已知瓶子的底面积为10平方厘米，请你根据图中标明的数据，计算瓶子的容积是多少立方厘米？

设计意图：巩固训练环节，设计内容基础与提高并重，体现了层次性与多样化。其中第3题引导学生自己提出问题，既巩固本节课学习的内容，又培养了学生的问题意识。同时，教师要有意识地给学生提供数学建模的脚手架，丰富学生的数学建模方式、方法与策略，这样久而久之，学生的模型意识就会逐渐培养起来。

四、反思回顾，思想延伸

1.回顾总结：通过这节课的复习，你印象最深的是什么？还有什么疑问？

2.赠言：在数学的天地里，重要的不是我们知道什么，而是我们怎么知道什么。

——毕达哥拉斯