“剥离”表象抵达抽象

黄金华

在小学阶段的各个学科领域中，数学眼光最能精准地直达事物的本质属性，表现为数学是检验真理的标准。《义务教育数学课程标准（2022年版）》指出：数学为人们提供了一种认识和探究现实世界的观察方式，需要用数学眼光从真实的现实世界中“剥离”出事物的物理属性，在问题情境中“去掉”表象，通过观察、操作、探究、感悟、迁移运用形成具有数学学科特点的抽象能力（数感、量感、符号意识）、几何直观、空间观念和创新意识。

一、数学眼光搭建数学与现实世界的桥梁

传统教学中，學生在学习中通过大量的训练获取优秀的考试成绩，教师的教往往直击知识点、考点，而情境、过程、逻辑关系、各种表征都被“忽视”和“跳过”，评价学生是否学会的方式很直接，训练量到位了分数就高，致使题海战术“盛行”了很长时间，学生课内外的学业负担繁重。原因是教和学脱离了真实的社会与生活经验，以至于多年以后很多人认为学数学没有什么用。

数学眼光作为数学学科的核心素养可以搭建数学和现实世界的桥梁，学生需要在一个相对开放的学习环境中，通过一次次从问题情境中提炼数学对象，一次次表达与交流，一次次呈现真实世界与数学的关系，凝练自己的数学眼光。

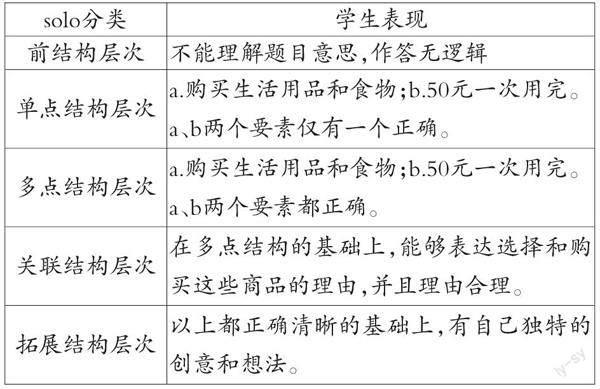
如，教学人教版一年级下册第五单元“人民币的认识”，调整为“综合与实践”领域的第一学段主题活动2“欢乐购物街”，学习目标和评价也应相应作出改变。从学情调研可发现学生对商品的价格有一定的意识，但由于人们已经适应了网上支付方式，一部分学生缺乏使用纸质人民币的经验，需要教师提供一个模拟交易的环境用货币模型开展交易，达成3个学习目标：①学生在活动中能准确辨认我国市面上流通的各种货币，认识元、角、分，知道元、角、分单位之间的关系；②在活动中学生能清晰地表达我想买什么、买几个，会询问物品价格或辨认物品价格标签；③在活动中通过交流、付钱、找零、反思购物合理性等，积累合理使用货币的经验，形成对货币多少的量感和初步的金融意识。学教评一体化的提出，评价成为提升学生思维层次的重要途径。该主题活动的评价案例如：给学生一张50元的购物券（一次用完，不设找补），到“超市”购买疫情期间必备生活用品和食物，根据solo分类评价分析学生学科素养的达成度和学生素养的融合度。具体如下：

二、数学眼光发展学生抽象能力

抽象能力主要是指通过现实世界中数量关系与空间形式的抽象，得到数学的研究对象，形成数学概念、性质、法则和方法的能力。在小学阶段的主要表现是数感、量感、符号意识，侧重于对经验的感悟。

量感主要指对于数量、数量关系及运算结果的直观感知。量感的形成要求学生在学习、操作过程中及日常生活经验中不断积累，经历在丰富的情境内运用多种表征方式反复体验、不断矫正优化的过程，由此可知量感的形成需要较为长期的沉淀，并非一蹴而就的。

如，二年级的主题活动“身体上的尺子”，学生先估一估拃、庹、步长、身高等身体上的“长度”，再通过精确测量自己身体的“长度单位”，从而用身体尺在开放的活动空间内量一量、估一估，比如课桌、门、窗、黑板有多宽，教室有多长、有多宽，校园里最粗的树干有多粗，路途较近的同学从学校到家有多远，家里的电视、沙发、餐桌等有多宽、有多高……通过丰富的动作表征、图形表征、符号表征、语言表征等体验单位的选择和长度的估测方法，形成学生个体独特的量感。

数学能力表征分为三个水平，再现、联系、反思。因此，主题活动学习之后的延伸、迁移运用要继续展开。比如，在教室里长期贴上或者画上长度为1厘米、1分米、1米的线段，学生在游戏和学习时能够随时看到、摸到和对比到，让量感在反复再现、与实物对照、反思矫正中得以抽象出来并充分建构。

三、数学眼光培育学生创新意识

2020年教育部郑富芝副部长提出创新人格的六要素：开放、自信、灵活、专注、合作和独立思考。“创新人格”把创新意识人格化了，这就使创新意识与教学之间的关系更为紧密，培育创新人格，就是新时代的新课程为“建设创新型国家服务”的一个新答案。

如，人教版六年级下册“圆柱与圆锥的体积关系”在学业测评中很容易出错，原因在于学生不能将两种立体图形的关系通过结构化搭建打通“等底等高”“等积等高”“等积等底”中变与不变的本质，从而发展空间观念和几何直观。通过圆锥体积的学习，对于“等底等高”的圆柱和圆锥，学生很容易理解和想象V圆锥=V圆柱或V圆柱=3V圆锥，运用这组关系学生能提出什么问题呢？自一年级开始学生积累了和差关系、倍比关系等数量关系，能够自觉迁移和运用，并产生新问题。如：“一个圆柱和一个圆锥，底面半径都是3厘米，高都是12厘米。它们的体积一共是多少立方厘米？”，从不同角度思考会得到不同的解决方法，进而复盘几何模型，从直观→抽象→直观，发展学生推理意识、空间观念。我们研究了“等底等高”的圆柱和圆锥，还会研究什么条件下的圆柱和圆锥的体积关系呢？再一次激发学生思考立体图形元素之间的关联，从而提出新的问题，还可以研究“等积等底”“等积等高”的问题，利用几何直观，将图示和算法一一对照，发现体积、底面积、高三个元素中若有2个相同，另一个则发生变化。渗透函数思想的同时，建立了结构化模型，发展了学生的创新意识和推理意识，为核心素养的发展找到了合适的学习路径。

总之，“三会”是一个有机的整体，具备整体性、一致性和阶段性，在教学中发展学生核心素养需要以培养“四基四能”为途径，拉长过程性学习，让评价成为学习的一部分，把“对学生的评价”调整为“为学生的评价”，也就是为学生的全面可持续性发展而评价，让数学眼光成为学生的关键能力。