三种孔形固体蓄热体的放热性能模拟研究
樊家辉 贾玉贵,2,3 赵建恩 张亚杰 王 硕 庞雪峰 秦 景,2 常宗越*
(1.河北建筑工程学院,河北 张家口 075000;2.河北省储能供热技术创新中心,河北 张家口 075000;3.河北省绿色建筑协同创新中心,河北 张家口 075000;4.张家口旅投工程建设发展有限公司,河北 张家口 075000)
0 引 言
近年来,全球能源转型与能源短缺相互伴随,世界各国竭力统筹协调能源绿色低碳发展与能源供应.太阳能、风能、水能等这些可再生能源在发电过程中的碳排放量很低,具有较高的环境友好性,但它们的发电量会受到时间和天气的限制,因此,这些新能源必须借用成熟的储能技术才能得以更好的发展.固体蓄热体是一种性能良好、应用广泛的蓄放热装置,它可以利用光电、风电对装置内部蓄热材料进行加热,当需要供暖时再放出热量,能很好地解决新能源不稳定和不可预见性等问题.研究发现,现有圆形孔固体蓄热体放热性能较差,有学者提出椭圆孔固体蓄热体较圆形孔放热性能更优[1],本文在此基础上提出了一种圆-椭圆相互交替的异形孔结构,并对三种孔形蓄热体在相同工况下进行了10小时放热过程模拟研究.最后对比分析了10小时末的放热完成度和放热均匀度,找出放热性能最优的孔形结构,为固体蓄热体的优化设计提供参考依据.
1 放热性能评价标准
放热完成度:指放热过程中某一时刻蓄热体放出热量与蓄热体理想蓄热量的百分比,计算公式如下所示[2].
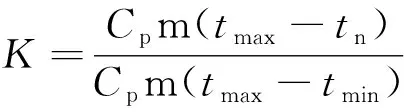
(1)
式中:K为放热完成度,单位为%;Cp为蓄热体的比热容,单位为[J/(kg·K)];m为蓄热体的质量,单位为kg;tmax为蓄热体的上限温度,单位为K;tmin为蓄热体的下限温度,单位为K;tn为n时刻时,蓄热体的平均温度,单位为K;
放热均匀度:指放热过程中某一时刻不同位置测点温度与砖体整体平均温度的离散状况,计算公式如下所示.
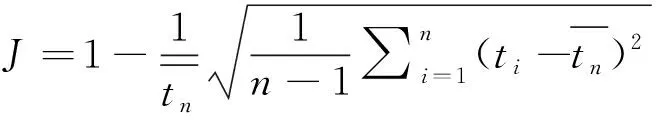
(2)
2 放热过程数学模型
固体蓄热体孔道内部对流换热是最重要的传热过程,放热过程中空气与蓄热体对流换热热量遵循牛顿冷却公式:
q″=α(Ts-Tf)
(3)
式中:q″为热流密度,单位为W/m2;α为对流换热系数,单位为W/(m·K);Ts为蓄热体温度,单位为K;Tf为流体温度,单位为K.
对固体蓄热体放热过程进行分析,得出空气与蓄热体对流换热量为:
Q=αAΔT
(4)
α=f(μ,λ,ρ,Cp)
(5)
式中:Q为孔道内流体与蓄热砖体之间的对流换热量,单位为W;α为孔道内流体与蓄热砖体表面的对流换热系数,单位为W/(m2·K);ΔT为孔道内流体与蓄热砖体之间的换热温差,单位为K;μ为流体的粘度,单位为Pa·s;λ为流体导热系数,单位为W/(m·K);ρ为流体的密度,单位为kg/m3;Cp为流体的定压比热容,单位为[J/(kg·K)].
努塞尔准数:表示对流换热强烈程度的一个无量纲数.
Nu=αD/λ
(6)
雷诺准数:反映流体流动强度的无量纲数.
Re=Duρ/μ
(7)
普兰特准数:反映流体物性对对流换热影响的无量纲数.
Pr=Cpμ/λ
(8)
迪塔斯-贝尔特方程:圆形直管内流体充分湍流时的表达式.
Nu=0.023Re0.8Prn
(9)
流体被加热时,n=0.4;流体被冷却时,n=0.3.此式适用于流体与壁面温度具有中等温差(不超过50℃)的场合,且L/D≥60,Pr=0.7-120.
本文研究中流体平均温度与固体表面温度的差值大于50℃,需要引入温差修正系数Ct,且本文研究中L/D<60,需要引入入口效应修正系数Cl.
气体被加热时
(10)
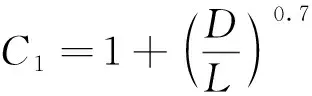
(11)
修正后的迪塔斯-贝尔特方程为:
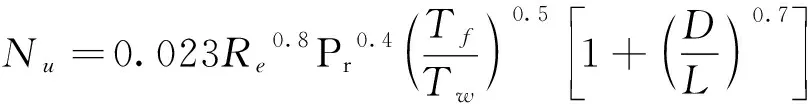
(12)
将以上各准数代入得对流换热系数α为:
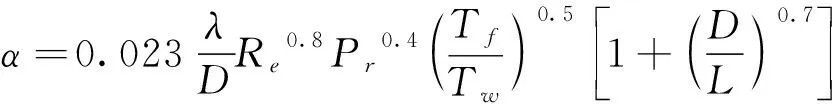
(13)
则孔道内流体与蓄热砖体之间的对流换热量为:
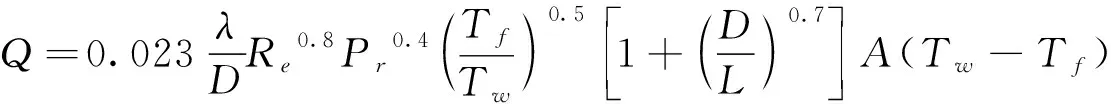
(14)
放热过程以空气作为换热介质,空气和蓄热砖体之间的换热方式为对流换热.放热过程为非稳态传热过程,其传热过程满足的质量守恒方程、动量守恒方程和能量守恒方程如下所示:
(1)质量守恒方程
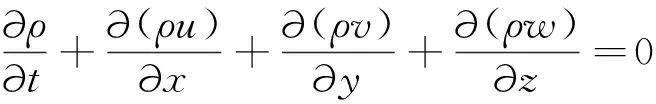
(15)
式中:ρ为流体密度;u,v,w分别代表x,y,z方向的速度;t为时间.
(2)动量守恒方程
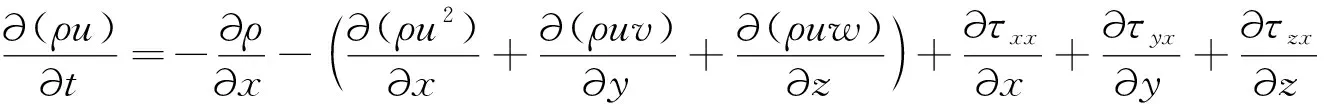
(16)

(17)
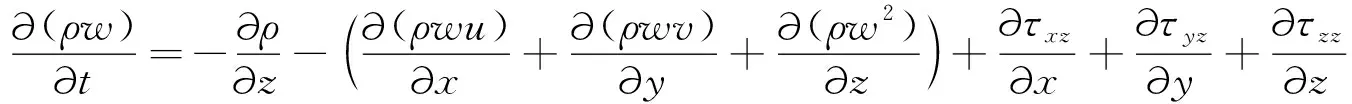
(18)
式中:p为流体在微元体上的压力;τxx,τxy,τxz为作用在微元体表面上的黏性应力τ的分量.
(3)能量守恒方程
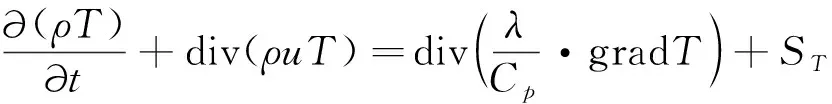
(19)
式中:T为热力学温度;λ为流体的导热系数;Cp为比热容;ST为黏性耗散量.
3 三种孔形固体蓄热体物理模型
本文主要研究固体蓄热体内蓄热体孔形对放热过程的影响,因此对模型做了简化处理.首先建立了相同孔隙率(孔道截面积占蓄热体截面积的百分比)的三种孔形固体蓄热体的物理模型,圆形孔固体蓄热体孔道结构为圆形,椭圆孔固体蓄热体孔道结构为椭圆形,异形孔固体蓄热体孔道结构为圆-椭圆相互交替的形状.蓄热体尺寸为1600×750×950(长×宽×高,单位:mm);保温外壳尺寸为2520×990×1070(长×宽×高,单位:mm),厚度为60mm;前后风道长都为400mm;进出口为圆形孔,直径为200mm.以下为三种孔形固体蓄热体的物理模型图:

图1 圆形孔蓄热体三维建模图 图2 圆形孔蓄热体左视图

图3 椭圆孔蓄热体三维建模图 图4 椭圆孔蓄热体左视图

图5 异形孔蓄热体三维建模图 图6 异形孔蓄热体左视图

图7 异形孔蓄热体剖面图1 图8 异形孔蓄热体剖面图2
对固体蓄热体的数值模拟分析做出如下假设:
(1)固体蓄热体内蓄热体各部分结构是连续且均匀的,且在放热过程中不存在质量与体积的变化;
(2)空气、氧化镁砖、外保温材料的物性参数恒定,不随温度进行变化;
(3)空气孔道内电阻丝构造忽略不计;
(4)保温外壳为绝热边界.
4 网格划分
利用Fluent Meshing软件进行采用非结构化网格进行网格划分,结果如图9所示.

图9 异形孔固体蓄热体体网格划分图
5 计算方法与边界条件设置
步骤(1):将网格文件导入Fluent中准备进行模拟计算;
步骤(2):本次模拟采用瞬态模拟,并且考虑重力加速度的影响,重力加速度设置为-9.8m/s2;
步骤(3):开启能量方程;
步骤(4):湍流计算采用的数学模型为RNG k-ε模型,湍流流动是一种高度不稳定的流动状态,具有非线性、随机性和多尺度特征.这些因素使得直接求解N-S方程比较困难,但人们已经能够通过配合适合的模型和CFD技术,取得与实际比较吻合的结果.本次模拟中采用的湍流模型为RNG k-ε模型,相较于标准k-ε模型它有效改善了ε方程的精度,方程对瞬变流和湍流漩涡能做到很好的反映;
步骤(5):辐射采用的数学模型为DO辐射模型,辐射模型的选择中,DO辐射模型考虑了所有光学深度区间的辐射以及存在局部热源的问题,且占用计算机内存也比较适中,故本文模拟计算采用DO辐射模型;
步骤(6):物性参数设置如表1所示;

表1 材料物性参数
步骤(7):边界条件设置:入口边界条件为velocity-inlet类型,入口风速为8m/s,温度为350K;出口边界条件为pressure-outlet类型;
步骤(8):用SIMPLE算法求解耦合关系,参数选择默认,在CFD软件中,主要提供了四种求解方法:SIMPLE、SIMPLEC、COUPLED以及PISO.SIMPLE算法适用于各种不同类型的流体问题,它只需要进行一次迭代即可得到解,在计算资源有限的情况下,SIMPLE算法需要内存较少.故本文模拟均选用SIMPLE算法作为数值模拟的求解器;
步骤(9):为了得到蓄热体温度随时间变化的参数,在监视器里面设置每1步时输出蓄热砖体平均温度的数值;
步骤(10):进行初始化设置,Fluent在进行迭代计算之前还需要对整个模型进行初始化设置,蓄热体初始温度设置为1073K;
步骤(11):本次仿真步长设为360s,步数设为100步,共10小时.
6 计算结果分析
如图10所示表示三种孔形固体蓄热体平均温度随时间变化情况.观察曲线图可以看出,蓄热体平均温度随时间变化呈现下降趋势,而且这种下降趋势随时间变化变得越来越缓慢,这是由于在放热初期蓄热体与空气存在较大温差,这种大温差会加剧空气和蓄热体之间的对流换热程度,当随着放热过程逐步进行,蓄热体温度在不断下降,两者之间的温差也会逐步缩小,对流换热效果逐渐变弱,温度下降趋势也会越来越慢.在放热的10小时末,圆形孔蓄热体平均温度由1073K降为530.77K,温差为542.23K;椭圆孔蓄热体平均温度由1073K降为510.81K,温差为562.19K;异形孔蓄热体平均温度由1073降为458.31K,温差为614.69K.10小时末异形孔蓄热体平均温度较圆形孔降低了72.46K,较椭圆孔降低了52.5K,通过放热性能评价标准中公式(1)可以算出:圆形孔固体蓄热体放热完成度为83.42%,椭圆孔固体蓄热体放热完成度为86.49%,异形孔固体蓄热体放热完成度为94.57%.由以上数据分析结合图10可以看出,在放热过程中,圆形孔固体蓄热体蓄热体平均温度总是最高,异形孔固体蓄热体蓄热体温度一直保持最低,且10小时放热过程完成后异形孔固体蓄热体放热完成度较圆形孔提高了11.15%,较椭圆孔提高了8.08%.

图10 三种孔形固体蓄热体平均温度随时间变化
利用CFD-post后处理软件,能够根据坐标位置提取截面上测点温度值.下图11为蓄热体前、中、后三个截面上温度测点的布置图.由于截面上温度分布上下左右呈现对称性,故每个截面选取了左下区域的6个测点,三个截面一共18个测点.

图11 截面上温度测点布置图
放热均匀度是评价固体蓄热体放热性能优劣的重要指标,根据公式(2),结合下表2,可以算出圆形孔蓄热体放热均匀度为81.58%,椭圆孔蓄热体放热均匀度为82.78%,异形孔蓄热体放热均匀度为85.07%.10小时放热过程完成后异形孔固体蓄热体放热完成度较圆形孔提高了3.49%,较椭圆孔提高了2.29%.

表2 放热10小时末三种孔形体测点温度数值
7 结 论
为探究固体蓄热体的放热特性,本文建立了圆形孔、椭圆孔和异形孔三种孔形的固体蓄热体物理模型并利用Ansys Fluent软件进行了数值模拟分析,并分析了蓄热体平均温度以及18个温度测点的数值变化等多组数据得出结论:异形孔固体蓄热体相较于圆形孔和椭圆孔增加了孔道内空气混乱程度、增强了蓄热体和空气之间的对流换热效果;且异形孔固体蓄热体在10小时放热过程后放热完成度为94.57%,较圆形孔提高了11.15%,较椭圆孔提高了8.08%;10小时放热过程后异形孔固体蓄热体放热均匀度为85.07%,较圆形孔提高了3.49%,较椭圆孔提高了2.29%.故认为在三种孔形比较中,异形孔固体蓄热体放热性能最好,本文为固体蓄热体的优化设计提供了参考依据.

