T形异形柱偏压性能有限元分析
翁维素 甄茗灿 乔春蕾 赵明坤 邵志新 潘本卿
(河北建筑工程学院,河北 张家口 075000)
0 引 言
钢管混凝土的研究可以直接追溯到上世纪末.钢管混凝土同时具备了混凝土抗压性能好和钢材抗拉性能好[1,2]的优点,且防火、延性等方面也优于传统的钢筋混凝土结构.多腔钢管混凝土更是将单腔钢管混凝土的缺点进行了补足,譬如阴角易破坏.小口径的钢管对核心混凝土的约束作用也是更加优秀.所以对多腔钢管混凝土的研究成为了近些年的主流.
朱昌星等[3]对单腔室和多腔室的T型截面钢管混凝土异形柱的承载机理进行了模拟分析.验证了多腔室的钢管混凝土的承载能力要优于单腔室钢管混凝土,且两种主要材料间的摩擦系数的变化,对试件整体的承载力没有影响.王亚晋[4]通过有限元软件分析,对矩形钢管混凝土和方形钢管混凝土的双向压弯的受力过程进行了分析,并根据相关数据绘出了多组有关方形钢管混凝土的力学关系,和各种变量对钢管混凝土构件的影响.李泉[5]、王周泰[6]等则在截面形式上进行了多种创新并进行了模拟和试验验证其力学性能.但大部分关于钢管混凝土的研究仅局限于理论和模拟,真正有试验参与的研究数量并不多,本文结合了以往的经验,设计了一种新型组合形式的异形柱,在试验的基础之上,研究其力学性能,并推导承载力计算公式.
1 有限元模型构成
1.1 本构模型
1.1.1 钢材本构
模拟采用的钢材本构模型参考文献[7]的本构模型(图1).密度取7.89×10-9t/mm3,杨氏模量取2.03×105MPa.屈服强度和极限强度取材性试验得到的数据的平均值.

图1 钢材本构关系模型
1.1.2 混凝土本构
混凝土采用塑性损伤模型(图2),混凝土受拉损伤模型参考[8].该模型对混凝土不利因素的考虑较为周全,可以更有效且更精准地对脆性材料进行仿真模拟.混凝土为各向异性材料,受压模型采用文献[9]提出的应力应变关系.该模型更贴切本试验中混凝土的条件.
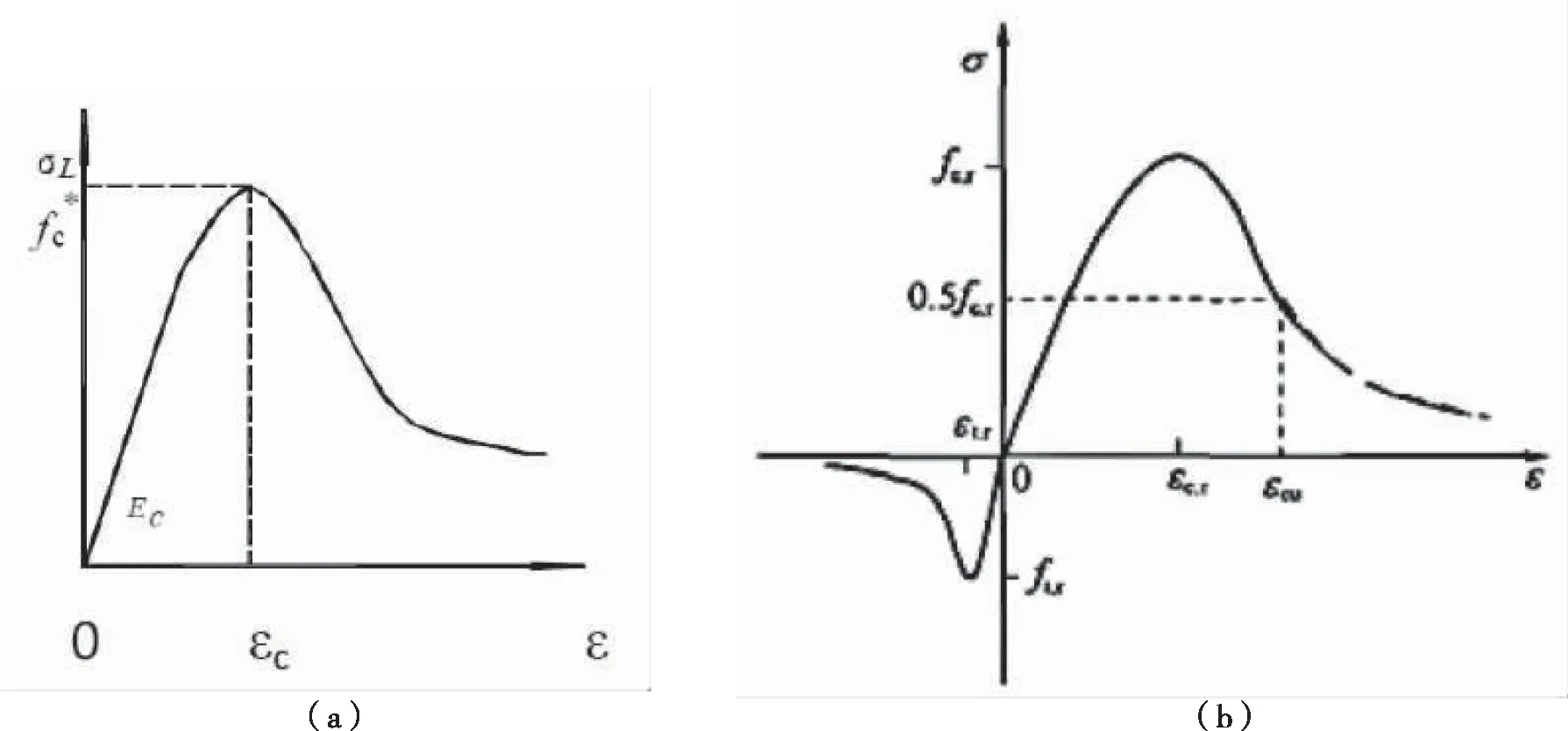
图2 受约束混凝土与非受约束混凝土单轴受压应力应变曲线
1.2 单元选取与网格划分
试验主体分为两部分,钢材和核心混凝土,钢材采用壳单元,核心混凝土采用实体单元,端部的加载板采用离散刚体.各部件的网格尺寸均为20mm.材料属性的定义以材性试验的数据为依据.试件的横截面设计如图3所示,有限元装配模型如图4所示.
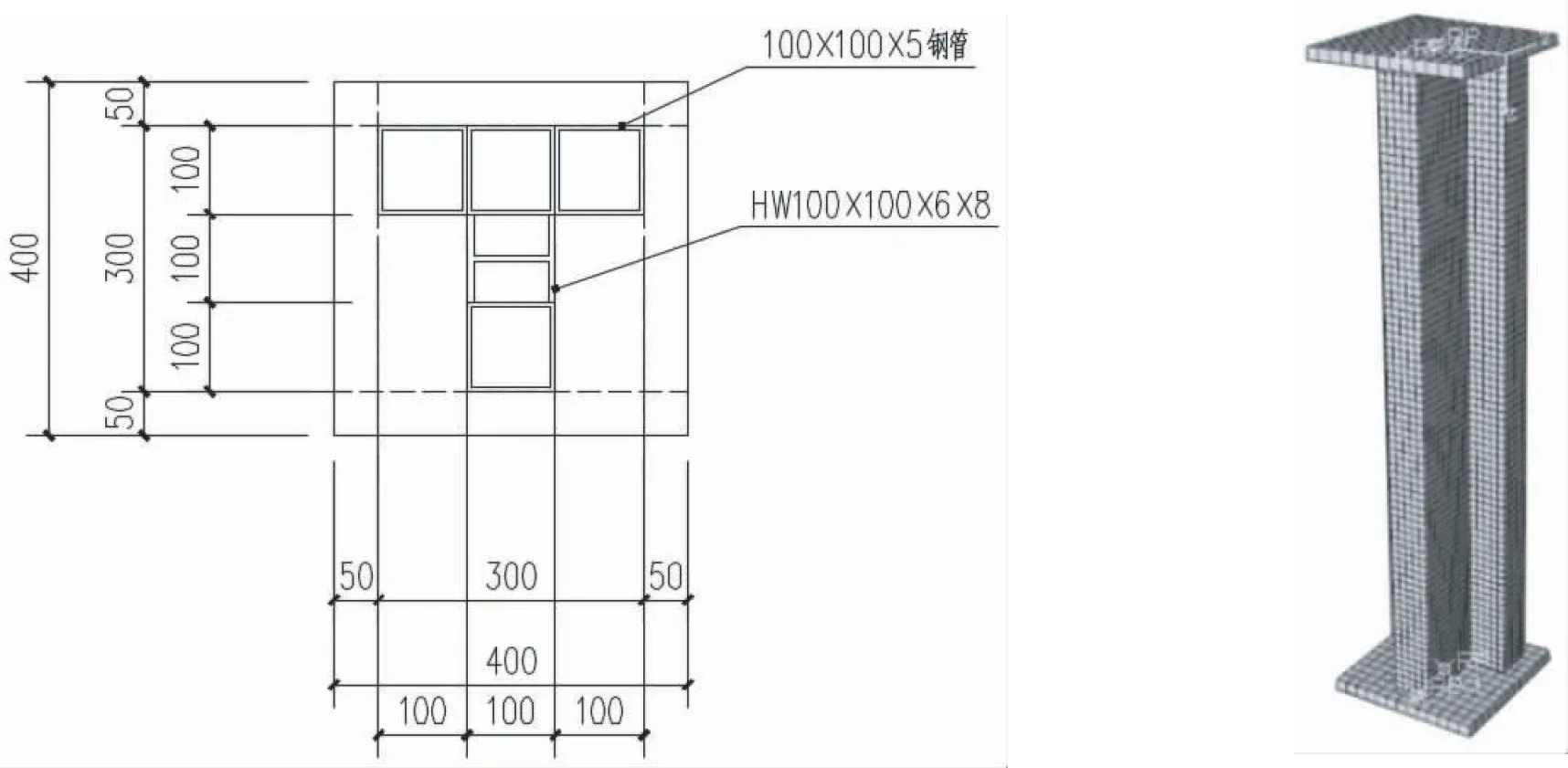
图3 试件截面图 图4 有限元模型
1.3 相互作用与边界条件设置
本模型需要设置的接触有钢材的焊缝,钢与钢的面面接触,钢与混凝土的面面接触.其中,试验过程中焊缝处没有发生破坏,故模拟时可将焊缝做绑定约束处理.钢管与混凝土间的粘结力等效为摩擦力,两者间的摩擦系数设为0.6,钢管与钢管间的摩擦系数设为0.3.
柱端约束为铰接,其中一端约束三个方向的平动自由度.试验采用位移控制加载,故另一端仅约束x轴和y轴的平动自由度,在z轴方向施加初始约束,以此来实现位移控制加载.
表1为有限元模拟试件的参数.其中,取ST-1与ST-11相同规格的试件进行了试验.
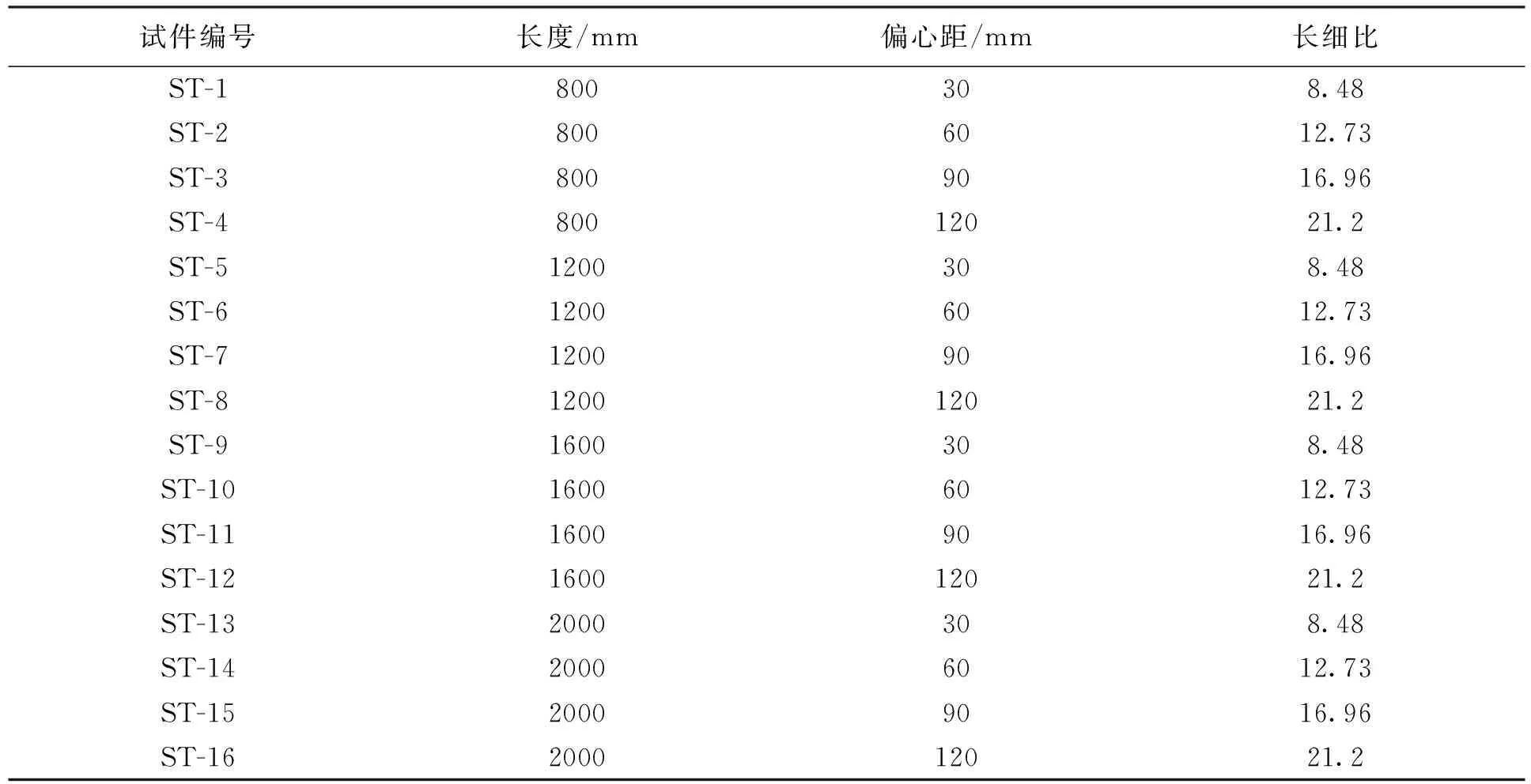
表1 有限元试件设计参数
2 有限元模型验证
2.1 破坏形态对比
图5为ST-1与ST-11的试验-模拟破坏形态对比图.

图5 破坏形态对比图
2.2 荷载-位移曲线对比
图6为两组荷载-位移对照曲线.试验取了一根长柱一根短柱,分别进行了偏压试验.由对比图可见,试验柱在加载前期,试验机横梁下降过程中对整个试验系统存在压实的过程,故曲线会出现偏移的现象.将该误差排除,对比两组曲线可见:弹性阶段试验与模拟的斜率基本相同,ST-11几近平行.极限承载力数值接近,曲线下降段趋势相同.综上所述,模拟的结果与试验的结果相近,可以作为理论分析的依据.

图6 荷载-位移曲线对比图
3 有限元模拟数据处理及公式推导
在理论基础之上,对36根不同偏心距和长细比的试件进行了有限元模拟,得到的极限承载力数值如图7所示,承载力单位为kN.
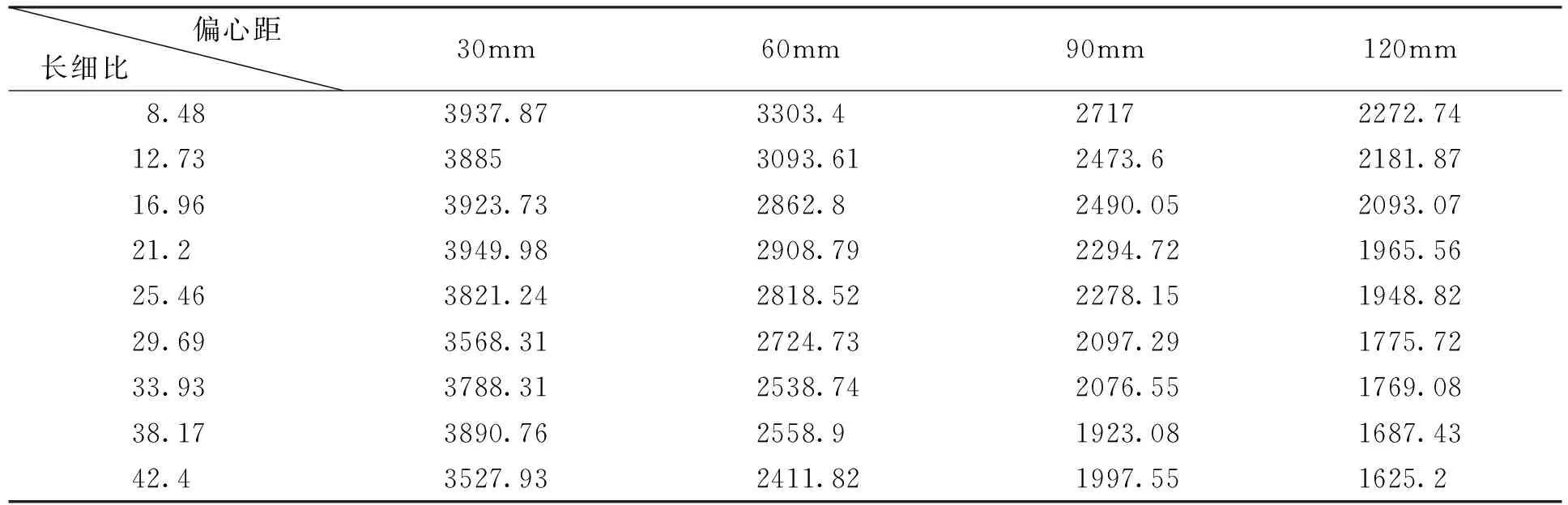
表2 极限承载力数值
分别以偏心距和长细比为自变量绘制与承载力相关的曲线,如图7、图8所示.
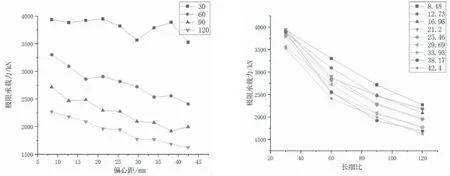
图7 偏心距-极限承载力曲线 图8 长细比-极限承载力曲线
由图可知,极限承载力随长细比和偏心距的增长,其变化趋势较为规律,且偏心距的影响更为明显.以此作为承载力公式推导的依据.
钢管混凝土承载力计算有三种理论,本文采用文献[10]中的统一理论作为理论基础,进行承载力公式推导.该理论的核心思想是将钢管和混凝土两种材料进行换算,使之成为一种混合材料,计算出组合材料的强度值,再推算承载力.原文中最初的计算方法更适用于圆形截面,本文所用钢管为方形,故需要对公式进行折减,计算公式如下:
(1)

其中,B和C用来表示两种主要材料在整体受力中起到的作用.B和C的计算公式中涉及到几个常系数,但多处文献对于该常系数的取值均有略微的差异,且不同形状的截面常系数也不同,即:
(2)
(3)
引入上述系数,可得组合抗压强度设计值的公式为:
(4)
式中:fsc为组合抗压强度设计值,单位MPa;ξ0为设计套箍系数,ξ0=αf/fc;f为钢材抗压、抗拉和抗弯强度设计值,单位MPa;fc为混凝土抗压强度设计值,单位MPa.
由此便得到了使用“统一理论”后组合材料的应力值,由此可得单根方钢管混凝土短柱的轴压强度设计值公式为:
N0=Ascfsc
(5)
式中:Asc为钢管混凝土截面面积,单位mm2.
长柱的承载力需要考虑长细比的影响,即在公式中加入φ,那么长柱的承载力计算公式为
N0=φAscfsc
(6)
式中:φ为轴心受压稳定系数.
通过以上公式推导,将本试验的数据带入,可得N0=5038.469kN.但统一理论中所提公式为纯钢管混凝土,本文所述试件存在一根型钢,直接将型钢的参数带入公式,会导致计算结果偏小,结合CECS159-2018[11]中的叠加理论,分别计算混合材料与型钢的承载力,在进行叠加,所得N0=5253.387kN.通过有限元模拟得到的短柱的N0=5538.61kN.对比三项数据可见,通过公式计算出来的结果偏于安全.总误差为5.1%,较为精确.
规范[12]中要求,钢管混凝土的长细比不得大于80.故将长细比λ≤80的试件的轴压承载力模拟数值进行回归和修正,以此来推导稳定系数φ,可得图9:
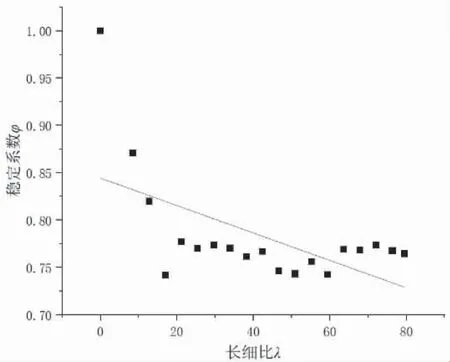
图9 长细比与稳定系数的关系
(7)
根据文献[10],推得钢管混凝土抗弯承载力标准值公式为:
(8)
(9)

为了使推导的公式更精确,增大了数据量,这些数据分别来自长细比8.48≤λ≤50.92,偏心距0≤e≤120mm试件的有限元模拟.将模拟所得数据绘制N/Nu-M/Mu关系曲线,可得图10:

图10 N/Nu-M/Mu关系曲线
对图形内的坐标进行拟合,可得异形柱偏压承载力N与M的关系式:
(10)
随着长细比λ的不同,N/Nu与M/Mu会有不同的关系,但整体趋势符合柱体偏压时轴力和弯矩的变化规律,其中,A、B、C是与自变量有关的系数,根据不同的长细比,A、B、C的取值也会有所不同,三个系数与长细比的关系如图11所示.
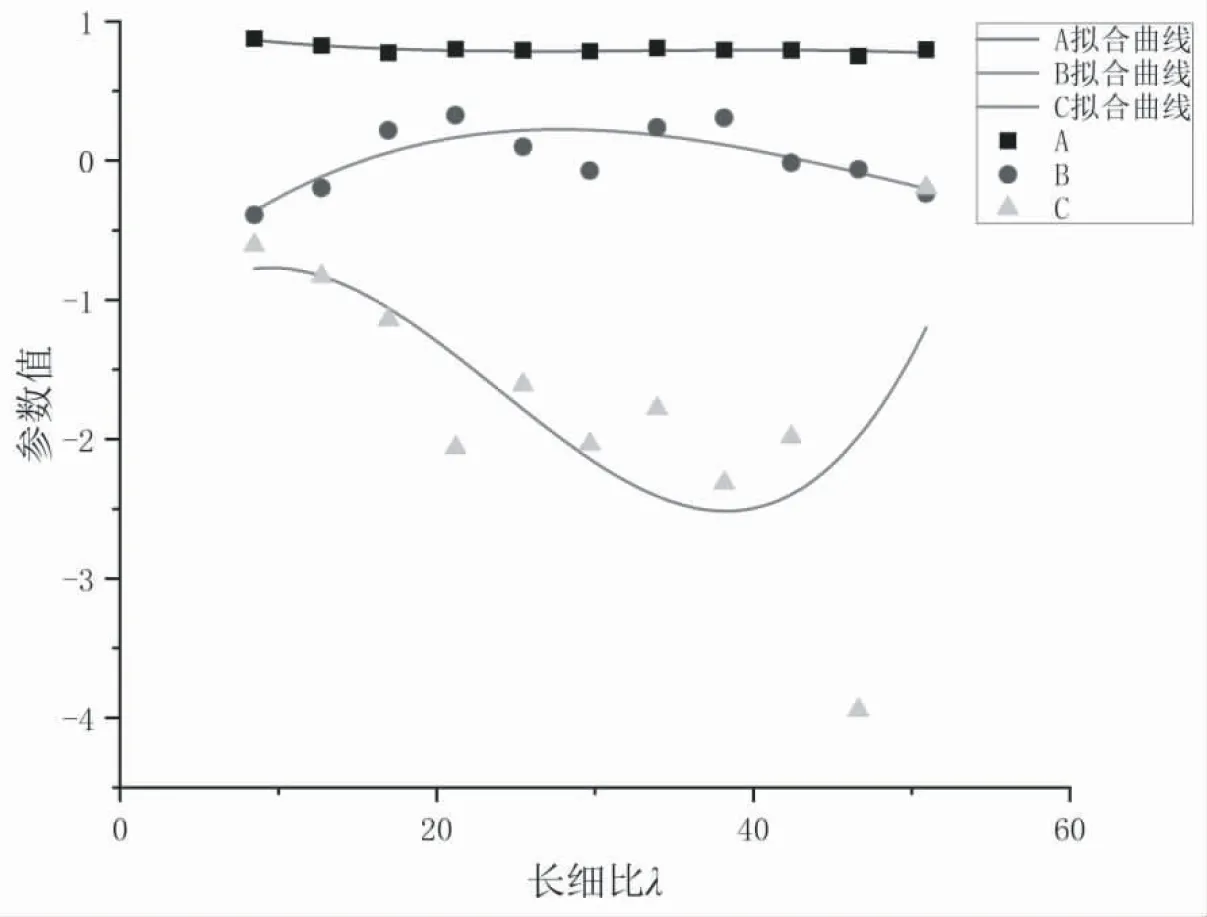
图11 计算参数与长细比的关系
对图中的数据进行拟合可得,各计算参数与自变量λ的关系式:
(11)
结合式(10)和式(11)即为本试验组合异形柱的承载力计算公式.
上述公式为理论研究下的承载力计算方法,考虑到实际应用中需要提高工作效率,上述公式便显得有些繁琐,不易便捷使用,故可以对其进行简化.对于这类公式的简化标准有两种,分别是截面边缘纤维屈服准则和截面部分发展塑性准则.前者的计算结果更为保守,后者对材料的利用率高.
在图11的基础上,用一条直线将试验曲线以下的部分包络起来(图12),这样可以保证在任意情况下,试件的计算承载力均在极限承载力之下,图中以点划线的形式体现.

图12 承载力计算公式简化
简化后的承载力计算公式为:
(12)
稳定验算公式为:
(13)
式中的其他参数均按钢结构设计规范中8.2.1[13]规定计算.
4 结 论
(1)分别对一根长柱和一根短柱进行了偏压试验,同时进行相应的有限元模拟,对照破坏模式及承载力变化.结果显示,试验与模拟的破坏形式相近,荷载变化规律相同,且试件具备良好的延性性能.
(2)对36根试件进行了有限元模拟,绘制了以偏心距和长细比为变量的图线.试件的极限承载力与偏心距和长细比的变化具有规律性,且变化稳定.随着两变量的增大,承载力的数值会减小.
(3)根据55组试验数据,推导出了该组合方式异形柱的承载力计算公式.

