基于单元模态应变能的梁结构分级损伤识别方法研究

吴文斌 杨海军,2* 马 磊 蒋亚贤 伍 莎

(1.河北建筑工程学院,河北 张家口 075000;2.张家口市工程力学分析重点实验室,河北 张家口 075000)

0 引 言

结构的损伤识别主要包括两个方面,一是结构损伤位置的判断,二是结构损伤程度的确定.

对于损伤位置的判断,刘文光[1]等推导了弹性薄板的单元模态应变能,并构造损伤识别指标对弹性薄板进行了损伤定位分析,得出单元模态应变能可以定位结构的损伤位置,但这种损伤识别方法确定的损伤是一个区域,真实的损伤位置在这一区域内,还需要通过优化算法对这一区域内的所有单元进行分析,判断出精确损伤位置与对应的损伤程度.

对于损伤程度的确定,通常是通过建立损伤结构的优化数学模型,结合损伤检测技术来进行的,遗传算法因其良好的寻优能力被广泛应用这一领域.缪炳荣[2]提出一种利用单元模态应变能与优化算法结合的损伤识别方法,该方法通过单元模态应变能确定结构的损伤区域,再结合遗传算法组合优化的思路对损伤区域的精确损伤位置与损伤程度进行判断.虽然能够最终确定损伤位置与损伤程度,但是初步定位的损伤区域过大,导致遗传算法的初始变量过多,计算量较大.

因此,基于目前损伤识别中存在的定位不精准、计算量大的问题,本文基于单元模态应变能和遗传算法,通过附加质量块的方法进行精确损伤定位以较小的计算量确定损伤程度,实现结构的分级损伤识别.

1 理论公式及原理分析

由文献[3-7]知,结构损伤后,由于损伤位置与损伤程度未知,结构自身力学属性的改变量无法确定,单元刚度矩阵难以确定,因此可用损伤前的单元刚度矩阵近似代替损伤后的单元刚度矩阵,研究表明,这样处理后的单元模态应变能对损伤更为敏感.因此,损伤前后的单元模态应变能及单元模态应变能变化率可表示为:

(1)

(2)

(3)

式中:MSEij、MSEijd分别表示损伤前后的第j个单元的i阶单元模态应变能,MSECRij表示第j个单元的i阶单元模态应变能变化率,{φij}表示第j个单元的i阶位移列向量,[Kj]表示第j个单元的单元刚度矩阵.

考虑到高阶模态时,由于噪声的影响,结构的振型频率将与实际情况偏差较大,因此,用单元的平均单元模态应变变化率作为损伤指标,这样将降低噪声的影响,更趋于合理化[6],公式如下:

(4)

结合式(1)、(2)、(4)可知,结构的单元模态应变能变化率受单元的节点位移列向量{φij}的影响,孙虎等[8]的研究表明,在结构的损伤区域施加质量块,结构的模态振型将发生改变,从而引起相应区域单元模态应变能变化率的改变,因此可以通过施加质量块的方式来达到精确定位损伤的目的.

在精确定位损伤位置的基础上,以损伤单元的单元模态应变能变化率为目标函数,利用遗传算法对损伤程度进行量化分析,判断损伤位置的损伤程度.

2 模型算例

2.1 建立有限元模型及损伤工况

以两端均为固定端的梁结构为研究对象,进行结构的损伤定位与损伤程度的判断.在ANSYS中用beam188梁单元进行有限元建模,弹性模量为2.1×105GPa,泊松比为0.26,密度为3150 kg/m2建立长为7.5 m,截面为0.3×0.5 m2的矩形截面梁,划分15个单元,有限元模型如图1,梁结构单元及节点编号如图2.

图1 梁结构有限元模型 图2 梁单元及节点编号分布

相比于无损伤工况,改变预设损伤位置的弹性模量,达到模拟损伤的效果.设定四个损伤工况进行分析研究,见表1:

表1 预设损伤工况表

2.2 确定损伤位置

2.2.1 初步损伤定位

分别对损伤工况与未损伤工况进行五阶模态分析,根据模态参数,结合公式(4)计算不同损伤工况下各个单元的平均模态应变能变化率,分布规律如图3.

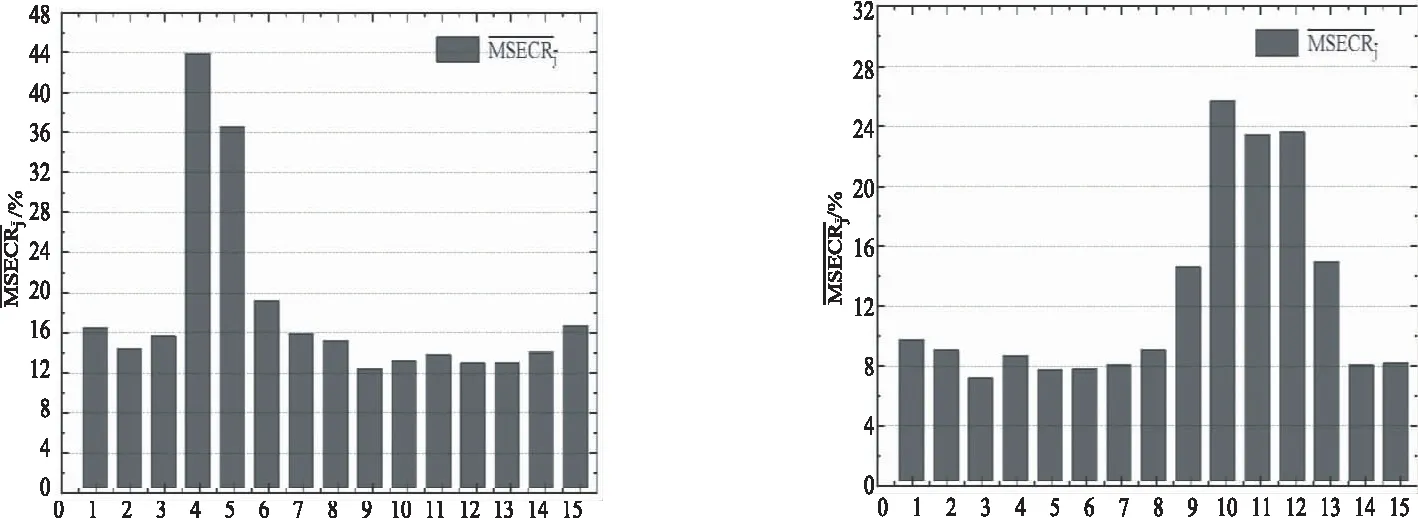
(a)工况1 (b)工况2

(c)工况3 (d)工况4图3 各单元平均模态应变能变化率

各工况下的损伤疑似单元见表2:

表2 各工况损伤单元及疑似损伤区域

由表2可知,通过单元的各阶平均单元模态应变能变化率可以得出相应的损伤位置(工况3、4中均有确定的损伤位置)或者损伤疑似区域(4个工况都有相应的损伤疑似区域),在损伤疑似区域内各单元的各阶平均单元模态应变能变化率不明显,即可能存在损伤单元,也可能不存在,因此要对该区域进行损伤二次定位.

2.2.2 二次损伤定位

分别对各工况损伤疑似区域的中间节点施加与整个损伤疑似区域质量相同的质量块,各工况质量块施加情况如下:

(1)对于工况1,损伤疑似区域包含4、5、6号节点,在中间5号节点施加与损伤疑似区域质量相等的质量块;

(2)对于工况2,损伤疑似区域包含10、11、12、13号4个节点,在中间11、12节点分别施加与1/2损伤疑似区域质量相等的质量块;

(3)对于工况3,损伤疑似区域包含4、5、6号3个节点,在5号节点施加与损伤疑似区域质量相等的质量块;

(4)对于工况4,损伤疑似区域包含9、10、11、12、13、14号6个节点,在中间11、12节点分别施加与1/2损伤疑似区域质量的质量块.

质量块数值模拟施加方法:通过定义MASS21质量单元,赋予相关节点质量属性,达到施加相应位置质量块的目的.

为控制单一变量,在分析4种损伤工况时,还要同时对无损伤结构的对应位置施加节点质量,然后再次进行模态分析,只需提取损伤疑似区域及邻近单元(左右各一个单元,以便于损伤疑似区域的数据进行对比)的平均单元模态应变能变化率进行分析,所得结果如图4.

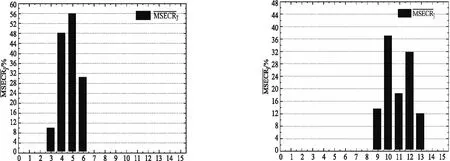
(a)工况1 (b)工况2

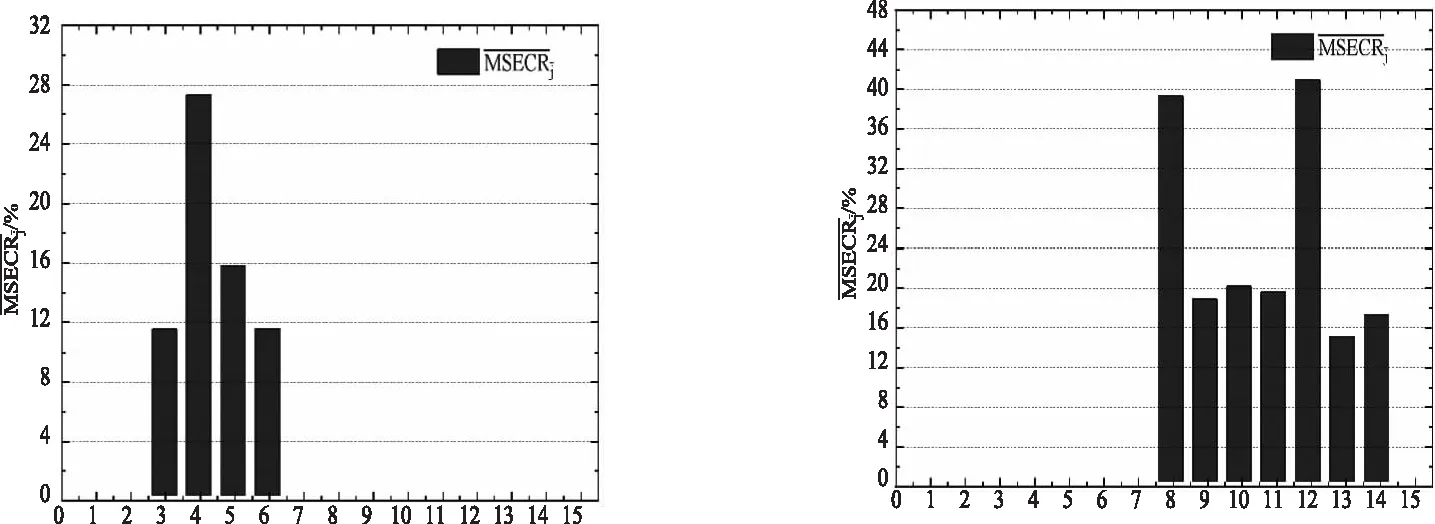
(c)工况3 (d)工况4图4 各单元平均单元模态应变能变化率

由图4知,在工况1、2、3、4各自的损伤疑似区域内,所确定的损伤位置分别为:工况1,4、5号单元;工况2,10、12号单元;工况3,4号单元;工况4,12号单元.

2.2.3 最终损伤定位结果

通过两次分析,最终确定损伤位置,见表3:

表3 两次损伤定位结果

由表3知,对于一次定位出现的损伤疑似区域施加质量块进行二次损伤定位,两次总的损伤定位结果与预设损伤位置相同,定位准确.

2.3 确定损伤程度

在确定损伤位置的情况下,对损伤程度进行判断,用遗传算法对损伤程度进行判断,设定初始种群为100,交叉概率0.8,变异概率0.6,利用Matlab与ANSYS联合仿真优化,以损伤单元在一次定位时的单元模态应变能为损伤量化值.各工况损伤单元在一次损伤定位时的平均单元模态应变能见表4:

表4 损伤单元在一次定位时的平均单元模态应变能

设遗传算法中变量对应的损伤单元的单元模态应变能变化率为βi(i=1,2,3,…),则各工况的适应度函数表达式为式(5)～(8):

fit1=|(β1-0.4378)+(β2-0.3638)|

(5)

fit2=|(β1-0.2560)+(β2-0.2354)|

(6)

fit3=|(β1-0.1643)+(β2-0.1901)|

(7)

fit4=|(β1-0.2130)+(β2-0.3331)+(β3-0.1781)|

(8)

式中:fit1～fit4分别为工况1-4的适应度函数值.

本算例迭代终止条件设为适应度函数值小于等于0.002,各工况迭代进化曲线如图5所示.

图5 迭代进化曲线

4个工况下利用遗传算法进行损伤程度的确定,得到各工况的迭代进化曲线终止代数、适应度最小值、对应的设计变量及损伤程度见表5:

表5 各工况损伤程度的量化分析表

由表5知,在确定损伤位置的情况下,利用遗传算法对损伤位置的损伤程度进行分析,在一定的遗传迭代后,能够判断出损伤位置损伤程度,并且与预设损伤情况相比较,该方法所识别的损伤程度误差均小于0.5%,接近预设损伤情况.

3 结 论

通过以梁结构为研究对象,提出一种以单元模态应变能变化率为基础,通过施加质量块方法进行损伤精确定位,再结合遗传算法进行损伤程度判断的分级损伤识别方法,得出以下结论:

(1)在损伤位置判断方面,利用单元模态应变能变化率进行损伤区域的初步确定,再通过施加质量块的方法进行损伤位置的二次确定,最终得到结构的精确损伤位置.

(2)在损伤程度确定方面,在损伤位置确定的基础上,利用遗传算法仅对损伤程度进行分析计算,解决了利用遗传算法进行损伤程度分析时由于虚假损伤造成计算量过大的问题.