不同结构形式的高层建筑的风振响应分析

潘乐鹏 张文祥 任淑萍 胡子良 郁 雯*

(1.河北建筑工程学院,河北 张家口 075000;2.河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075000)

0 引 言

现如今,城市用地随着人口的不断增多正变得越来越紧张,越来越多的建筑向着高层甚至超高层方向发展,像风这类的水平荷载对建筑的影响也越来越大.

目前,许多学者对高层建筑的风振响应问题进行了研究,风振响应是在脉动风作用下产生的,王修琼教授对脉动风谱中的Davenport谱系数K与地面粗糙度关系进行了研究[1],在计算高层建筑风振响应时,对风谱的使用进行了优化,提高了高层建筑中风振响应计算时数据的准确性;在进行风振响应计算时,大多数采用软件模拟的方法,像朱洁和刘润富首先利用MATLAB软件进行风速时程响应分析,然后通过ANSYS软件进行高层建筑的风振响应计算,得到建筑物顶端的加速度时程响应,并对建筑物的舒适度进行了研究[2,3];王新锋利用ABAQUS软件进行风振响应分析,并为高层建筑剪力墙的布置提供了一些建议[4].这些研究,都体现出研究风对高层建筑的重要性.

为了比较框架核心筒与剪力墙这两种结构形式在受到风荷载作用下,表现出的不同振动响应情况,本文使用ANSYS软件,建立起这两种结构形式的有限元模型,借助王修琼教授对Davenport谱的研究,分析出这两种结构形式在风荷载作用下的动力响应的不同.

1 有限元模型

1.1 工程概况

运用ANSYS软件进行有限元模型的建立,案例一为框架核心筒结构[5],如图1所示,案例二为剪力墙结构,如图2所示.均采用总层数为28层,层高为3m,总高度为84m,长为36m,宽为26m的模型.采用钢筋混凝土作为工程中构件材料.

图1 框架核心筒结构 图2 剪力墙结构

在进行模型建造时,选用合理的构件尺寸,两种模型的尺寸规格如下表所示.

表1 框筒结构构件截面尺寸表

表2 剪力墙结构构件截面尺寸表

将建立好的模型进行布尔运算,对模型中重叠构件进行合理划分.框筒结构共有2296个构件,剪力墙结构共有2072个构件.

1.2 材料属性

本案例构件中采用的材料均为钢筋混凝土,在定义材料时,为计算方便,将钢筋与混凝土两种材料作为一种新材料插入到软件中,材料属性如表3所示.

表3 材料属性表

对于材料的拉压特性,将钢筋的抗拉强度作为新材料的抗拉屈服强度,强度为2.95×108Pa,混凝土的抗压强度作为新材料的抗压屈服强度,强度为2.5×108Pa.

2 模态分析

将楼面恒荷载和活荷载以均布力的形式施加到楼板上,底部采用固接方式.通过ANSYS中的Workbench平台,进行静力学分析,完成静力学分析后,进行结构的前八阶的模态响应分析[6,7],得到两种结构的各阶响应频率和变形情况.现将前三阶的变形图和前六阶的振型情况列出,如下所示.

一阶振型 二阶振型 三阶振型 一阶振型 二阶振型 三阶振型图3 框筒结构前三阶振型图 图4 剪力墙结构前三阶振型图

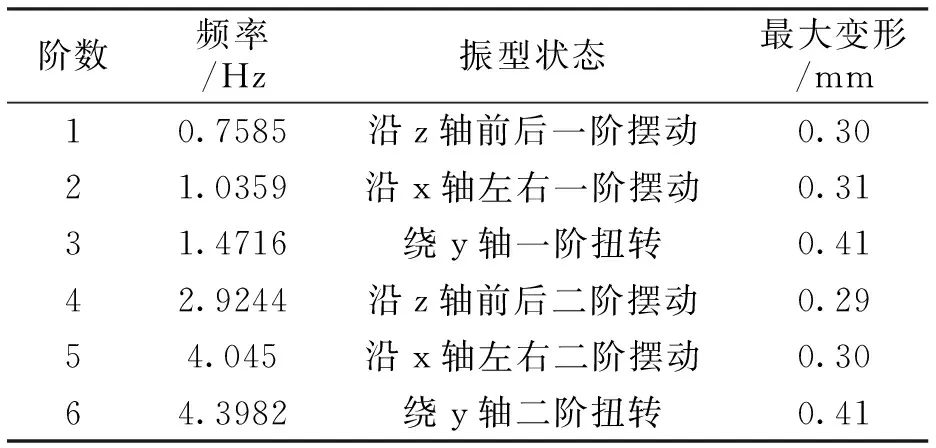
表4 框筒结构各阶振型表

表5 剪力墙结构振型表

通过模态分析结果,得到了两种结构形式的前8阶的自振频率和振型特点.根据表格,可以得出:在前三种模态响应中,前两种为不同方向上的平动,第三种为转动.框筒结构的一阶自振周期为1.318s,剪力墙结构的一阶自振周期为1.286s.框筒结构最大变形为第一阶扭转振型,变形量为0.41mm,剪力墙结构最大变形也为第一阶扭转振型,变形量为0.49mm,两种结构形式模态的最大变形都不超过1mm.

3 响应分析

3.1 响应计算

根据建筑结构荷载规范[8],本案例层高大于30m,并且第一阶自振周期大于0.25s,考虑脉动风对高层建筑振动的影响,风谱选用目前最具有代表性的Davenport谱.其表达式为

(1)

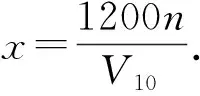
根据建筑结构荷载规范,地面粗糙度类别选择B类,10m高度处平均风速取10.7m/s.根据文献[1]K取0.00215.可以得到风速功率谱密度函数[9],如右图所示.

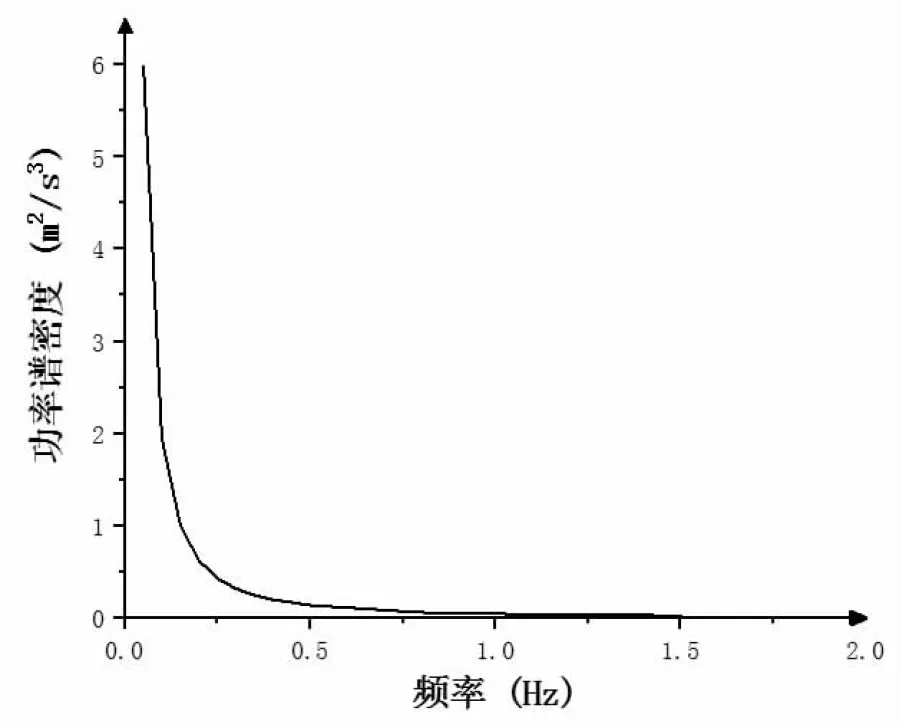
图5 风速谱密度曲线

将功率谱密度函数输入到Ansys Workbench中,沿z轴方向施加脉动风频率谱,进行动力响应[10]计算.

3.2 结果分析

计算完成后,选取模型中响应最大的节点,来反映风振响应的位移变化情况.根据模态分析中测得的各阶频率,得到节点在该频率下的变化情况,左侧为框筒结构产生的位移,右侧为剪力墙结构产生的位移,如下表.

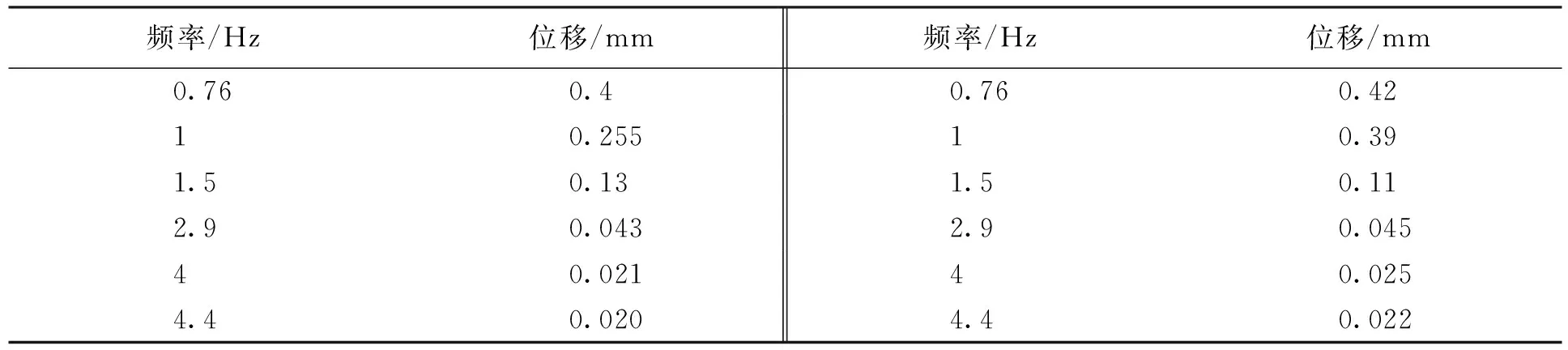
表6 节点部分频率下的位移

通过风振响应的结果,框筒结构和剪力墙结构的最大的节点位移均位于顶层处,两种结构均在第一阶固有频率下达到最大位移,框筒结构最大位移为0.4mm,剪力墙结构最大位移为0.42mm,可以求得框筒结构的最大加速度为0.23m/s2,剪力墙结构的最大加速度为0.25m/s2,两种结构的位移量差距不大,根据其他频率下结构产生的位移,框筒结构受风作用产生的位移量小于剪力墙结构产生的位移,说明框筒结构形式的抗风性能略好于剪力墙结构的抗风性能.

4 结 论

根据基于ANSYS软件风荷载作用下不同结构形式的风振响应的模拟,得到以下结论:

(1)求得两种结构形式的自振频率和变形情况,并均在第一阶扭转振型下产生最大变形,框筒结构的最大变形小于剪力墙结构.

(2)两种结构形式在风荷载作用下时,风振响应的最大位移和最大加速度均在第一阶频率时产生.

(3)通过两种结构的最大位移和加速度比较,框筒结构形式的抗风性能优于剪力墙结构的抗风性能.