不同腐蚀缺陷下的HL 级抽油杆疲劳分析研究

王尊策 李玉贺 李 森 康红兵 彭振华 丁 雯

（1.东北石油大学机械科学与工程学院；2.中国石化西北油田分公司工程技术研究院）

随着石油行业的不断发展，许多油田都已进入中、高含水期开采阶段，再加上产出液中含H2S、CO2等酸性物质，使得抽油杆柱腐蚀速率大幅增加［1～3］。据塔河油田近三年检泵作业统计，共217 井次因抽油杆失效检修，其中因腐蚀原因造成检修的井有148 井次，占总作业量的68.2%。说明抽油杆腐蚀会严重影响油田的正常生产。

李大建等基于H 级抽油杆物理实验数据的数学统计处理分析，明确了H 级抽油杆极限疲劳强度等力学特性［4］。牛彩云等基于修正API 理论与奥金格理论，建立了H 级抽油杆最大许用应力计算方法与折算应力计算方法，为H 级抽油杆科学设计和应用提供了依据［5］。何文江等通过理化性能试验、金相组织分析等方法，对30CrMoA HL 级抽油杆进行失效分析，发现抽油杆表面所有裂纹均起源于表面腐蚀坑底部，该区域易发生截面突变从而导致应力集中［6］。张旭昀等依据圣维南原理和第三强度理论，分析出缺陷长度、宽度和深度变量在相互作用下对套管等效应力最大值的影响规律［7］。丁雯等根据损伤力学原理建立抽油杆疲劳损伤演化模型，采用有效应力法与有限元软件对多种损伤形式下的HL 级抽油杆疲劳寿命进行数值模拟，为判断抽油杆的疲劳寿命提供依据［8］。虽然上述研究均得到了较好的成果，但大多都是基于点蚀开展的，而在实际生产中抽油杆的腐蚀损伤形式复杂多样，需对多种腐蚀缺陷类型开展相关研究。

笔者在前人研究的基础上，应用ANSYS 有限元分析软件，通过数值模拟分析了不同腐蚀缺陷下各影响因素对HL 级抽油杆疲劳寿命的影响程度，并比较了不同缺陷下对抽油杆疲劳寿命的影响差异。

1 正常抽油杆疲劳仿真模拟

1.1 三维建模与网格划分

根 据SY/T 5029—2013 行 业 标 准［9］，用 三 维软件建立标称值22（7/8″）的抽油杆模型，并对其进行适当简化，简化后的抽油杆模型如图1 所示。用兼容性较强的六面体网格为主（Hex Dominant）的方法在ANSYS Workbench 中对其做网格划分［10］，并对结构较为复杂的位置做局部网格加密（图2）。

图1 简化后的抽油杆模型

图2 Hex Dominant 网格划分

1.2 模拟仿真

塔河油田大部分抽油机井光杆最大载荷在100 kN 左右，故在此工况下对其进行模拟分析。以30CrMoA 材料的HL 级抽油杆试样为例，材料的弹性模量为215 GPa，泊松比为0.3，密度为7 850 kg/m3，屈服强度为795 MPa，抗拉强度为965 MPa。杆头一端施加固定约束，另一端施加交变拉应力，应力比为0.1，抽油杆疲劳损伤形式为高周疲劳，用Goodman 疲劳模型对其进行修正［11］。用ANSYS 里的Fatigue Tool 工具模拟抽油杆在这种工况下的疲劳寿命，结果如图3 所示。可以看出抽油杆应力集中部位在于杆体与镦粗凸缘结合的变截面处，拉应力载荷最大等效应力为267.35 MPa，最小疲劳寿命4.9847×107次，与现场实验数据基本吻合。

图3 100 kN 下抽油杆等效应力与剩余疲劳寿命云图

2 两种腐蚀缺陷下抽油杆疲劳仿真模拟

2.1 腐蚀坑缺陷抽油杆数值模拟

如图4 所示，在危险截面处创建腐蚀坑缺陷，模拟抽油杆在100 kN 交变载荷下的疲劳寿命情况。模拟因素与水平见表1，共设计16 组模拟，模拟结果见表2，方差分析结果见表3。

表1 腐蚀坑缺陷下模拟因素及水平设计

表2 腐蚀坑缺陷抽油杆模拟设计及结果

表3 腐蚀坑缺陷抽油杆方差分析结果

图4 腐蚀坑缺陷抽油杆网格图

根据100 kN 交变载荷作用工况下的模拟结果绘制各影响因素的效用曲线，如图5 所示。经多组模拟仿真分析，腐蚀坑深度和半径对抽油杆疲劳寿命都有显著影响（α=0.01），蚀坑半径比深度的影响作用更显著。随着蚀坑深度的增加，抽油杆疲劳寿命减小；随着蚀坑半径减小，抽油杆疲劳寿命减小。

图5 腐蚀坑缺陷抽油杆各影响因素与剩余疲劳寿命关系曲线

2.2 环形腐蚀缺陷抽油杆数值模拟

如图6 所示，在危险截面处创建环形腐蚀缺陷，模拟因素与水平见表4，模拟结果见表5，方差分析结果见表6。

表4 环形腐蚀缺陷下模拟因素及水平设计

表5 环形腐蚀缺陷抽油杆模拟设计及结果

表6 环形腐蚀缺陷抽油杆方差分析结果

图6 环形腐蚀缺陷抽油杆网格图

根据100 kN 交变载荷工况下的模拟结果绘制各影响因素的效用曲线，如图7 所示。经多组模拟仿真分析，环形腐蚀深度和宽度对抽油杆疲劳寿命都有显著影响（α=0.01），腐蚀宽度比腐蚀深度影响作用更显著。随着环形腐蚀深度的增加，抽油杆疲劳寿命减小；随着环形腐蚀宽度减小，抽油杆疲劳寿命减小。

图7 环形腐蚀缺陷抽油杆各影响因素与剩余疲劳寿命关系曲线

3 多元线性回归模型的建立

根据方差分析结果，对两种腐蚀损伤形式中各损伤因素与疲劳寿命进行多元线性回归，建立HL 级抽油杆各损伤因素与疲劳寿命间的关系。

100 kN 交变载荷作用下腐蚀坑缺陷抽油杆中各影响因素与疲劳寿命间的关系可表示为：

100 kN 交变载荷作用下环形腐蚀缺陷抽油杆中各影响因素与疲劳寿命间的关系可表示为：

对式（1）、（2）进行方差分析，结果列于表7。

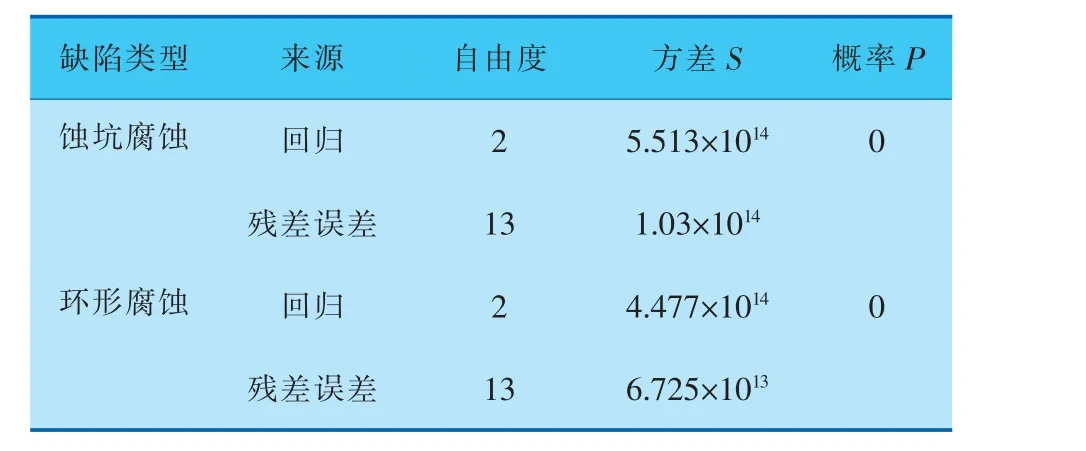
表7 各腐蚀缺陷抽油杆多元线性回归模型的方差分析结果

为验证方差分析的可靠性，利用调整决定系数公式计算两组回归方程的调整决定系数［12］。

调整决定系数计算公式为：

式中 k——回归变量个数；

n——试验次数；

R——调整决定系数；

SE——误差平方和；

ST——总平方和。

根据式（3）计算出两组调整决定系数分别为0.921、0.904，说明两组回归方程均具有指导意义。

4 两种腐蚀缺陷抽油杆剩余疲劳寿命对比

为了验证蚀坑腐蚀和环形腐蚀对抽油杆疲劳寿命的影响程度，根据模拟结果对两种腐蚀损伤形式抽油杆进行对比，结果见表8。经对比分析，对于同等工况下两种不同损伤形式的抽油杆，环形腐蚀抽油杆的疲劳寿命要比蚀坑腐蚀抽油杆的疲劳寿命更短。

表8 100 kN 工况下两种腐蚀缺陷抽油杆剩余疲劳寿命对比

5 结论

5.1 抽油杆在服役过程中最大应力集中在杆体与镦粗凸缘结合的变截面处，此处易发生疲劳断裂。

5.2 利用方差分析各影响因素对抽油杆疲劳寿命的影响程度。腐蚀坑半径（环形腐蚀宽度）对抽油杆疲劳寿命影响极其显著，并与其呈正相关性；腐蚀深度对抽油杆疲劳寿命影响显著，与其呈负相关性。

5.3 建立不同工况、不同腐蚀损伤类型下的多元线性回归模型。利用回归模型可定量描述各腐蚀损伤因素与疲劳寿命之间的关系，对判断HL 级抽油杆的安全性能具有指导意义。

5.4 对两种腐蚀损伤形式下的HL 级抽油杆剩余疲劳寿命模拟结果进行对比分析。在同等工况下，环形腐蚀抽油杆的剩余疲劳寿命要比蚀坑腐蚀抽油杆的剩余疲劳寿命更短。