设备负载对轮系啮合刚度及啮合力的影响研究

陈亚辉　王泽鹏　陈田田　华君

摘要：设备在运转过程中会产生波动负载，导致轴系中轮系的啮合刚度及啮合力产生变化。根据能量法构建直齿轮时变啮合刚度计算模型，并建立考虑负载耦合影响的啮合刚度修正模型。在平行轴弯－扭耦合齿轮传动系统下，采用Newmark时域算法计算，对比无波动负载和考虑波动负载影响下的齿轮时变啮合刚度差异，并分析设备负载对平行轴齿轮啮合刚度及啮合力的影响。同时，通过行星轮系相位调谐公式的推导，分析设备负载对行星轮系啮合力的影响。结果表明，设备的波动负载会对齿轮啮合力产生边频调制影响；对于均布型行星轮系，当中心轮受到传动轴系的设备波动负载影响时，相位调谐模型将失去其调谐规律。

关键词：设备负载；轮系；啮合；相位调谐

中图分类号：TH132.41 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.03.009

文章編号：1006-0316 （2023） 03-0055-08

The Effect of Equipment Load on Meshing Stiffness and Meshing Force of the Gear Train

CHEN Yahui，WANG Zepeng，CHEN Tiantian，HUA Jun

（ Wuxi Branch of Harbin Marine Boiler and Turbine Research Institute， Wuxi 214000， China ）

Abstract：The device generates fluctuation load during operation， which leads to the changes in meshing stiffness and meshing force of the gear system. In this paper， the spur gear time-varying meshing stiffness calculation model based on the energy method and a meshing stiffness correction model considering the load-coupling effect are established. Under the transverse-torsional coupling gear transmission system， the Newmark time domain algorithm is used to compare the differences of meshing stiffness under no fluctuate load and fluctuate load and analyze the effect of equipment load on meshing stiffness and meshing force of the parallel shaft gear. At the same time， the impact of equipment load on meshing force of planetary gears is further analyzed through the derivation of the planetary phasing formulas. The results indicate that the fluctuant load of the device will generate boundary modulation effect on the gear meshing force， and in terms of the equally spaced planetary gear set， when the center gear is affected by the fluctuant equipment load， the tuning law of the phasing model will no longer work.

Key words：equipment load；gear system；meshing；phasing theory

齿轮系在啮合运转时往往受到设备负载波动的影响，这使得轮系振动与啮合状态相互耦合，导致齿轮啮合刚度、啮合力等啮合参数发生改变，齿轮的啮合状态变得复杂。

目前关于设备负载对轮系啮合刚度、啮合力影响的研究相对匮乏。Xinghui等[1]研究了齿轮扭转振动系统的参数稳定性与齿轮刚度调频的联系。Kim等[2]研究了齿轮横振系统响应与轮系时变啮合参数的关系。袁运博等[3]研究了在外部波动负载下，同时计入横振和扭振响应对平行轴齿轮啮合刚度和系统响应的影响。

行星齿轮系传动凭借其结构紧凑、传动比大、承载能力强、传动效率高等优点，近年来越发受到传动机械的青睐，被广泛应用在汽车、船舶、风电等工程技术领域[4]。行星齿轮传动多采用行星轮均布型结构，以达到较好的减振降噪工程目的[5]，学者们总结出行星齿轮相位调谐理论来解释该工程现象。

行星齿轮相位调谐理论是一种有效的行星齿轮传动系统降噪措施，最早由Schlegel等[6]通过实验研究发现，他们在直齿行星齿轮传动系统上实现了11 dB的降噪效果。Palmer等[7]利用实验研究也验证了利用相位调谐来实现行星齿轮传动降噪的可行性及有效性。Platt[8]则通过实验研究进一步验证了相位调谐在斜齿行星齿轮传动上的降噪效果。

在相位调谐理论研究方面，Seager[9]利用静态传递误差动态激励模型，以直齿行星齿轮传动为研究对象，揭示了中心轮齿数、行星轮个数与系统振动模式间的映射关系。Kahraman[10]和Blankenship[11]也利用静态传递误差动态激励模型，忽略啮合刚度的时变性，以斜齿行星齿轮传动为研究对象，研究了构件所受激励力的相位特征与构件振动模式之间的映射关系，提出了相应的相位调谐理论。Parker[12-13]直接从啮合力出发，提出了基于具体的行星齿轮动力学模型的研究思路，将啮合力表示为傅里叶级数展开形式，推导各个中心轮的受力情况，给出了行星轮个数、中心构件齿数和谐次阶数与中心构件受力特征之间的映射关系。

但相位调谐理论是在轮系理想啮合的条件下建立的，当考虑外部设备负载的振动影响时，相位调谐理论的机理是否依然成立，尚待研究。

针对上述问题，建立含设备负载耦合影响的齿轮啮合刚度修正模型，在平行轴齿轮弯扭耦合系统下，研究设备负载对齿轮啮合刚度、啮合力的影响。然后结合经典均布行星轮系相位调谐理论，分析解释负载波动对行星轮系相位调谐理论的影响。

1 平行轴轮系动态啮合模型的建立

1.1 外啮合齿轮啮合刚度模型

式中： 为齿轮因赫兹接触效应产生的刚度，N/m； 、 、 为直齿轮因弯曲、剪切、压缩效应，根据能量法推导所产生的刚度，N/m；E为齿轮弹性模量，Pa；L为齿轮的有效齿宽，mm；ν为齿轮泊松比； 为啮合分力与合力的接触变化角，rad； 为基圆半齿角，rad； 为齿轮的瞬时啮合角，rad； 为理论压力角，（°）； 、 为驱动轮和从动轮的齿数； 为驱动轮圆频率，rad/s；t为时间，s； 、 为驱动轮和从动轮的齿顶圆半径，mm； 、 为驱动轮和从动轮的基圆半径，mm； 为理想安装中心距，mm； 为理论齿顶压力角，（°）； 和 分别为驱动轮和从动轮的接触变化角因子，rad。

可见齿轮的啮合刚度模型中，中心距、瞬时啮合角、重合度、驱动轮接触变化角因子与横向振动产生了耦合；啮合分力与合力的接触变化角、啮合周期与扭转振动产生了耦合。

2 负载对平行轴轮系模型的影响

采用经典齿轮弯扭耦合模型[15]，研究负载对平行轴轮系动力学模型的影响。齿轮副建立弯扭耦合模型，驱动电机及负载建立扭转模型。

齿轮齿宽16 mm、模数2.117 mm、压力角20°、重合度1.6456、杨氏模量2.07×1011 Pa、泊松比0.254，其余参数如表1所示。

设负载形式为周期性波动负载，将其表示为傅里叶级数形式：

式中： 为设备负载的直流恒定分量； 为负载谐波幅值； 为负载的谐波频率； 为负载谐波相位；l为谐次； 为大于等于1的自然数。

设负载激励为单频波动负载，研究在单频负载激励下，齿轮的啮合激励变化规律。

采用Newmark时域法，计算无波动负载和考虑波动负载（单频波动负载）影响下的齿轮时变啮合刚度，如图2所示。

图2（a）的长周期啮合刚度曲线显示，波动负载对啮合刚度的幅值进行了调制，且曲线呈现周期性波动。这是由于在横振作用下，齿轮的中心距、啮合角、重合度发生变化，进一步影响了啮合刚度积分公式的求解。图2（b）的短周期啮合刚度曲线显示，波动负载对啮合刚度的频率进行了调制。这是由于在扭转振动作用下，每个齿的啮合周期发生了改变，进而产生调频现象。

负载影响下的齿轮啮合刚度频域对比如图3所示。可以看出，在齿轮啮合基频（1000 Hz）及其倍频（2000 Hz、3000 Hz）附近產生了调频调幅谱线（±13 Hz），调制幅度围绕中心频率依次递减。相比于无波动负载，有波动负载情况下的啮合刚度曲线中心频率幅值下降，能量分散至边频调制带。

负载影响下的齿轮啮合力频域对比如图4所示。可以看出，齿轮啮合力基频（1000 Hz）及其倍频（2000 Hz、3000 Hz）附近同样产生了调频调幅谱线（±13 Hz），调制幅度围绕中心频率依次递减。有波动负载情况下的啮合力曲线中心频率幅值下降，能量分散至边频调制带。该规律与啮合刚度调制规律一致。

可知，在设备负载影响下，平行轴齿轮系的啮合会产生调制现象，频谱特征变得复杂。基于该理论基础，对考虑负载影响下的行星轮系相位调谐模型进行研究。

3 负载对行星轮系相位调谐模型的影响

3.1 经典相位调谐理论

对于均布行星轮系，中心轮的受力频谱特征在某种条件下可以实现理论上局部谐次的力平衡，以达到较好的减振降噪工程目的[12]。

对行星轮系中的中心轮进行受力分析，如图5所示。

中心轮啮合力在横向、纵向、扭转方向上的表达式为：

式中： 和 分别为中心轮受到的啮合力在横向和纵向的投影，N； 为啮合扭矩，Nm；  为驱动轮半径，m。

忽略啮合力的直流分量，将 表示为傅里叶级数展开形式：

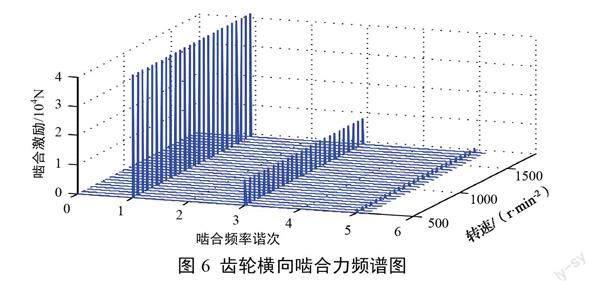
行星轮系啮合力频谱分析如图6所示。横向啮合力频谱成分为基频、3倍频和5倍频，2倍频及4倍频被抑制消失。这是由于相位调谐因子k≠1且N－1时，抑制啮合力，k＝1或N－1时，激起啮合力，该结论与经典相位调谐理论一致。

行星轮系啮合扭矩频谱分析如图7所示。啮合扭矩频谱成分为啮合4倍频，1、2、3倍频被抑制消失。调谐因子k≠0时抑制啮合扭矩，k＝0时激起啮合扭矩，该结论与经典相位调谐理论一致。

3.2 负载对行星轮系相位调谐理论的影响

由第2节可知，负载会引起平行轴轴系横向及扭转振动，进而影响轮系的中心距、啮合角、重合度、啮合周期等啮合信息，导致齿轮的啮合刚度、啮合力频谱出现调频调幅特性，调制频率为设备的波动负载频率。

对于行星轮系，在设备波动负载的影响下，齿轮的啮合力可写为：

式中： 为啮合力的调幅函数； 为啮合力的调频函数。

当中心轮受到传动轴系的设备负载影响时，受力如图8所示。

中心轮与各行星轮之间会产生啮合力的调幅函数和调频函数，导致边频调制现象，使得中心轮的受力无法再进行合并同类项化简式（18）。相位调谐理论将不再遵循表2中的规律，失去相应的调谐规律。

4 结论

根据能量法建立外啮合齿轮时变啮合刚度计算模型，并建立考虑设备负载耦合影响的齿轮刚度修正模型，分析负载对齿轮啮合刚度、啮合力的影响。结合经典均布齿轮相位调谐模型，分析设备负载对均布行星轮系调谐模型的影响，并得出如下结论。

（1）设备负载影响下，平行轴齿轮副的中心距、啮合角、重合度、啮合周期等啮合特征产生变化，啮合刚度及啮合力频谱在齿轮啮合基频及其倍频附近产生了调频调幅谱线，调制频率为设备负载频率，调制幅值围绕中心频率依次递减。

（2）相比无波动负载的啮合刚度曲线，考虑波动负载影响情况下的啮合刚度及啮合力曲线中心频率幅值下降，能量分散至边频调制带。

（3）当中心轮受到传动轴系的设备负载影响时，中心轮受力无法再进行合并同类项的公式化简。相位调谐理论将失去相应的调谐规律。

参考文献：

[1]Xinghui，Qiu，Qinkai，et al. Analytical investigation on unstable vibrations of single-mesh gear systems with velocity-modulated time-varying stiffness[J]. Journal of Sound and Vibration，2014，333（20）：5130-5140.

[2]Kim W，Hong H Y，Chung J. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation[J]. Journal of Sound and Vibration，2010，329（21）：4409-4421.

[3]袁运博，刘震，何涛，等. 波动负载对齿轮系统振动特性及边频调制影响研究[J]. 振动工程学报，2019，32（3）：526-533.

[4]邱星辉，韩勤锴，褚福磊. 风力机行星齿轮传动系统动力学研究综述[J]. 机械工程学报，2014，50（11）：3-36.

[5]Inalpolat M，Kahraman A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets[J]. Journal of Sound and Vibration，2009，323（3）：677-696.

[6]Schlegel R G，Mard K C. Transmission noise control approaches in helicopter design[C]. ASME Design Engineering Conference，New York，1967：DE-58.

[7]Palmer W E，Fuehrer R R. Noise control in planetary transmissions[J]. Earthmoving Industry Conference，Peori，1977：SAE paper 770561.

[8]Platt R L，Leopold R D. A study on helical gearplanetary phasing effects on transmission noise[J]. VDI Berichte，1996，1230：793-807.

[9]Seager D L. Conditions for the neutralization of excitation by the teeth in Epicyclic Gearing[J]. Journal of Mechanical Engineering Science，1975，17（5）：293-298.

[10]Kahraman A. Planetary gear train dynamics[J]. Journal of Mechanical Design，1994，116（3）：713-720.

[11]Kahraman A，Blankenship G W. Planet mesh phasing in epicyclic gear sets[C]. UK：Proceedings of International Gearing Conference Newcastle，1994：99-104.

[12]Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J]. Journal of Sound and Vibration，2000，236（4）：561-573.

[13]Parker R G. Suppression of Planet Mode Response in Planetary Gear Dynamics Through Mesh Phasing[J]. Journal of Vibration and Acoustics，2006，128（2）：134-142.

[14]Xihui，Liang，Ming，et al. Evaluating the time-varying mesh stiffness of a planetary gear set using the potential energy method[J]. Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science，2014，228（3）：535-547.

[15]BartelmusW. Mathematical modelling and computer simulations as an aid to gearbox diagnostics[J]. Mechanical Systems & Signal Processing，2001，15（5）：855-871.

收稿日期：2022-04-22

作者簡介：陈亚辉（1995－），男，江苏无锡人，硕士，助理工程师，主要研究方向为机械传动及振动特性，E-mail：664912295@163.com。