谐波转矩对机车传动系统动态特性的影响研究
金潇 刘林 黄珊 周子伟


摘要:牵引电机谐波转矩对由牵引电机、齿轮传动、轮轨接触等组成的铁路机车传动系统动态载荷、振动噪声等动态特性有着重要影响。本文基于国内某交流电力机车牵引电机的结构参数和功能特点,通过虚位移原理获得了脉动谐波转矩,并将其作为激励输入到建立的考虑齿轮传动系统动态啮合的车辆-轨道垂-纵耦合动力学模型中,研究了牵引电机谐波转矩对机车传动系统动态特性的影响规律。研究结果表明,谐波转矩会加剧传动系统齿轮动态啮合力和动态传递误差的幅值波动,从而进一步导致轮轨动态相互作用力波动程度加剧,但受轴重转移影响,轮轨黏着系数均方根值增载位轮对小于减载位轮对,且增载位轮对受谐波转矩影响较小,而减载位轮对受谐波转矩影响较大。
关键词:铁路机车;齿轮传动;虚位移原理;谐波转矩;黏着系数
中图分类号:U262.4 文献标志码:A doi:10.3969/j.issn.1006-0316.2023.03.005
文章编号:1006-0316 (2023) 03-0027-07
Effects of Harmonic Torque on Dynamic Characteristics of Locomotive Transmission System
JIN Xiao1,LIU Lin1,HUANG Shan1,ZHOU Ziwei2
( 1.National Innovation Center of High Speed Train, Qingdao 266111, China;
2.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China )
Abstract:The harmonic torque of traction motor has a vital effect on dynamic load, vibration noise and other dynamic characteristics of the locomotive transmission system which is composed of traction motor, gear transmission, wheel-rail contact, etc. In this paper, based on the structure parameters and functional characteristics of the traction motor of an AC electric locomotive in China, a vehicle-track vertical-longitudinal coupled dynamics model considering the dynamic meshing of gear transmission system is established. And by using the void displacement principle, the ripple harmonic torque is calculated and input into the established coupled model as an excitation to explore the effect law on the dynamic characteristics of locomotive transmission system. The results show that the harmonic torque will aggravate the fluctuation amplitude of the dynamic mesh force and dynamic transmission error, which results in more fluctuation of the dynamic interaction between the wheels and the rail, while the RMS value of wheel-rail adhesion coefficient on the load increment wheelset is less than the load reduction wheelset under the effect of the axle load transfer. In addition, the load increment wheelset is less affected by the harmonic torque, while the load reduction wheelset is more affected by the harmonic torque.
Key words:railway locomotive;gear transmission;void displacement principle;harmonic torque;adhesion coefficient
牽引电机作为电传动系统和机械传动系统的中间执行环节,是一种具有强耦合性的机电能量转换装置,其主要功能是借助定子与转子间的电磁耦合效应产生力矩,从而驱动与转子相连接的机械系统工作。在铁路机车中,常采用逆变器供电给牵引电机,在牵引过程中,逆变器会形成巨大的谐波干扰。输入牵引电机的谐波电压将在转子和定子绕组中产生大量的谐波电流,这不但会加大定、转子间的损耗,例如铁耗和铜耗,还会在气隙间形成转向与转速各不相同的旋转磁场,进而导致电机的转矩和转速产生振荡[1-2]。杨顺昌等[3]从基本电磁关系和建立等效电路的角度出发,系统分析了电机基波转矩和谐波转矩的特点,并提出其具体的计算公式。李伟等[4]利用虚位移原理计算异步电机中的谐波转矩,并进行了实例计算。在此基础上,部分学者针对轨道车辆上的谐波转矩对车辆动力学性能的影响开展了研究[5-6],发现,谐波转矩对轨道机车整车动力学性能影响不明显,但对齿轮传动和牵引电机等动力传递路径上的关键部件动态特性影响较大。
作为将牵引电机输出的转矩传递到轮对从而驱动轨道车辆或列车向前行驶或产生制动力的关键环节,齿轮传动系统在工作过程中,其时变啮合刚度与传递误差等内部激励也会对轨道车辆系统动态行为产生影响。基于翟婉明[7]提出的车辆-轨道耦合动力学理论,Chen等[8]建立了综合考虑齿轮动态啮合效应的车辆-轨道垂向耦合动力学模型,探究了齿轮传动系统对机车动力学响应的影响,还进一步建立考虑齿轮动态啮合效应的机车-轨道垂-纵平面耦合的动力学模型[9],通过测试数据验证了模型的有效性和准确性,并在牵引工况下研究了齿轮副时变啮合力对车辆轴重转移等动态响应的影响。上述文献研究证实,齿轮传动系统与铁路机车系统之间,特别是针对动力传递路径上的关键旋转部件,具有明显的动力学耦合作用效应。
本文主要通过牵引电机主要参数计算得到研究工况条件下的波动幅值最大的牵引电机前4次谐波转矩,并将其与基波转矩相互叠加,由此得到牵引电机谐波转矩激励。将该谐波转矩输入到综合考虑齿轮动态啮合效应的车辆-轨道垂-纵平面耦合的动力学模型中,通过数值仿真,在驱动工况下研究牵引异步电机存在的谐波转矩对轨道车辆传动路徑上主要部件的动态响应特征的影响。
1 异步电机谐波转矩分析与计算
1.1 谐波转矩分析
对于机车,通常采用三相交流异步电机进行牵引,其谐波转矩一般分为稳定谐波转矩和脉动谐波转矩。通常,稳定谐波转矩对车辆系统的影响不明显,可以忽略不计。对于异步电机,考虑基波的n个(n为正整数)旋转磁场会产生(n2-n)个脉动谐波转矩,由于采用对称分布的三相绕组,能有效消除电动势中3及3的倍数次谐波,所以,对三相整流负载会形成(6n±1)次谐波。由于前4次谐波成分的幅值占主导地位,所以在计算脉动谐波转矩时,主要考虑由5、7、11和13次谐波形成的脉动转矩。定义:
2 机车-轨道垂-纵耦合动力学模型
本节建立了综合考虑齿轮动态啮合效应的机车-轨道垂-纵平面耦合的动力学模型[9],如图3所示。为方便观察,图中仅显示了单节机车的1/4动力学模型示意图。
从图3可看出,该机车系统由上至下主要包括车体、构架、轮对、牵引电机、齿轮传动系统等部件及连接各部件的弹簧-阻尼单元。在传统车辆系统动力学分析中,根据多刚体动力学理论,大多将车体、转向架、轮对和牵引电机等部件视作刚体,各个刚体之间通过悬挂单元连接并相互作用。齿轮传动系统的主要功能是将牵引电机输出的电磁转矩传递给轮对,通过在轮轨接触界面产生纵向蠕滑力进而驱动车辆前行或形成制动;转向架与车体之间通过牵引杆,使车体产生纵向运动,牵引杆用弹簧-阻尼单元表示。由于牵引杆相对于水平方向有一个倾角,从而使垂向和纵向运动之间产生耦合效应。以vx的方向为车辆纵向运行方向。
轮轨接触部分采用Hertz非线性弹性接触理论计算,为:
式中: 为轮轨垂向接触力,N;G为轮轨接触常数; 为轮轨间的弹性压缩量,m; 、 分别为车轮和轨道在轮轨接触点的垂向位移,m; 为轮对在钢轨上的纵向位置,m; 为车轮和轨道表面在接触点的垂向几何不平顺,m; 为轮轨纵向蠕滑力,N; 为轮轨接触界面的黏着系数。
转向架与齿轮传动系统的连接如图4所示,齿轮传动系统能够考虑扭转振动,并在垂、纵方向上将构架和轮对的运动耦合起来。有:
式中: 为齿轮时变啮合力,N; 为齿轮啮合的时变刚度,N/s; 为齿轮啮合阻尼,N·s/m,文献[10]对啮合齿轮时变啮合刚度的求解模型进行了改进,提出精度更高的计算方法; 为齿轮啮合动态传动误差;R为齿轮的基圆半径,m; 为齿轮的角位移,rad;下标g和p分别表示大齿轮和小齿轮;e为轮齿几何误差,包括制造误差、装配误差、齿廓缺陷和齿廓修形等;i为第i位电机; 为压力角,(°); 为齿侧间隙,m。
根据达朗贝尔原理,建立考虑齿轮动态啮合效应的车辆系统的运动方程组,为:
式中:M、C和K依次为机车系统的质量、阻尼和刚度矩阵; 、 和 依次为位移、速度和加速度向量; 为车辆系统动态相互作用力,包括轮轨力、齿轮啮合力等。
采用快速显式积分方法进行数值求解,其数值积分格式为:
式中:Δt为积分的时间步长;下标j、j-1和 j+1分别表示当前积分步t=jΔt、上一积分步 t=(j-1)Δt、下一积分步t=(j+1)Δt;φ、ψ为控制积分方法特性的独立参数,通常取0.5。
3 结果分析与讨论
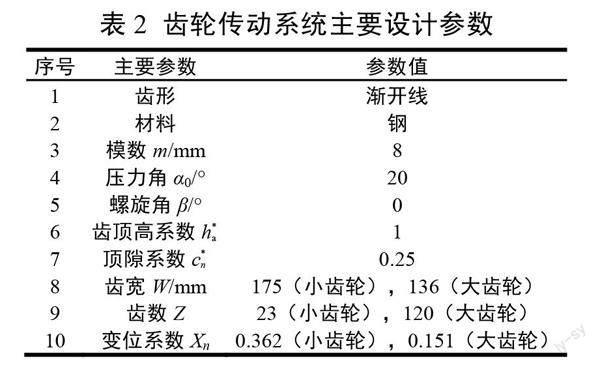
本文涉及的机车齿轮传动系统大、小齿轮主要设计参数如表2所示,其他结构参数见文献[9]中的表1。通过给出的齿轮参数,可计算得到齿轮在啮合周期内的时变啮合刚度,如图5所示。轮轨黏着与轨面状态和相对蠕滑速度相关,本文采用我国在干燥轨面状态下得到的实测黏着系数曲线[11]进行计算,其与相对蠕滑速度的关系曲线如图6所示。需要说明的是,本文建立的综合考虑齿轮动态啮合效应的机车-轨道垂-纵平面耦合的动力学模型已在文献[9]中与现场试验测试数据进行对比验证。
根据建立的考虑齿轮动态啮合效应的机车-轨道垂-纵平面耦合的动力学模型,为了对比分析谐波转矩对传动系统动态性能的影响,仿真设置牵引电机转子通过齿轮副将有谐波和无谐波的牵引转矩传递到轮对上,从而使车辆逐渐加速至80 km/h后保持匀速行驶,仿真时间为120 s。仿真结果中车速与时间的变化曲线关系如图7所示。
齿轮啮合动态传递误差和齿轮动态啮合力随速度变化的趋势如图8和图9所示。可以看出,传动系统的动态响应随着速度的增加波动逐渐变大,这是由于在轨道不平顺影响下,随着机车速度的提升,车轮与轨道间的动态相互作用逐渐加剧。在有谐波转矩的工况中,传动系统的响应较无谐波工况下的响应有很大幅度的波动,在低速工况中尤为明显。另外,在机车速度接近80 km/h时,齿轮啮合动态传递误差出现为负的情况,即出现齿轮正反啮合的现象,在有谐波干扰时啮合力正反波动会更大。可见谐波转矩会加剧传动系统的振动冲击。
提取1、2位轮对在有无谐波转矩影响下轮轨垂向接触力和黏着系数均方根值随速度的变化趋势如图10和图11所示。
从图10可以看出,轮轨垂向接触力随车速的变化趋势与图8和图9相同,其均值约等于净轴重;不同的是,当无谐波干扰时,1位轮对的轮轨垂向接触力明显小于2位轮对的轮轨垂向接触力,由图4可知,当机车向前行驶时,齿轮啮合力在垂向上的分力对1位轮对有减载而对2位轮对有增载的作用,从而导致同一构架上不同轮对出现轴重转移现象,但这一现象随着车速的增加会逐渐减弱。而谐波转矩的存在会导致轮轨垂向接触力产生大幅波动,致使转向架点头运动加剧,从而导致轴重转移波动现象,较无谐波转矩工况在更低车速就会出现同一构架上两轮对的轮轨垂向接触力交替大于对方的情况。
从图11可以看出,1,2位轮对在有无谐波转矩影响工况下,轮轨黏着系数均方根值随车速的升高都呈现逐渐降低的趋势;但受轴重转移现象的影响,增载位轮对的黏着系数均方根值小于减载位轮对的黏着系数均方根值,且增载位轮对黏着系数均方根值受谐波转矩影响较小,而减载位轮对黏着系数均方根值在谐波转矩影响下将会出现较大波動。由此可见,谐波转矩通过造成传动系统振动冲击从而影响轮轨接触状态、轮轨黏着,这无疑会对机车的黏着控制以及车轮磨耗形成较大挑战。
4 结论
本文通过建立综合考虑齿轮动态啮合效应的机车-轨道垂-纵平面耦合的动力学模型,同时考虑牵引电机谐波转矩、齿轮时变啮合刚度、轨道随机不平顺等激励的影响,在设定的工况条件下,研究了上述激励在牵引加速过程中对铁路机车传动路径上各部件动态特性的影响,通过分析主要得出如下结论:
(1)在无谐波转矩影响时,机车传动系统主要受到轨道随机不平顺和齿轮时变啮合刚度的激励作用,随着车速的升高,轮轨间动态作用加剧,齿轮传动动态传递误差波动幅值逐渐增大,造成齿轮啮合力波动变大,从而加剧传动系统内部的动态相互作用。另外,当车速接近80 km/h时,动态传递误差出现为负的情况,即齿轮在牵引工况中出现反啮合的现象。在有谐波转矩时,由于其脉动特性,会造成机车传动系统振动响应波动幅值变大,加剧传动系统的扭转振动,但这一情况随着车速的提升有所减缓。
(2)齿轮传动系统在啮合过程中对1位轮对有增载作用,对2位轮对有减载作用,从而导致同一构架上的两轮对与钢轨垂向作用力呈现一大一小的现象,且随着车速的增加,这种加减载的轴重转移现象会逐渐减弱。当谐波转矩叠加作用时,会导致齿轮动态传动误差和啮合力产生大幅振荡,从而导致轮轨垂向接触力出现较大幅度周期性波动,进而致使在较低车速时出现交替轴重转移的现象,从而加剧构架的点头运动。
(3)受轴重转移的影响,同一转向架上的两个轮对与钢轨的黏着系数均方根值出现增载位小而减载位大的现象,且增载位轮对与钢轨的黏着系数受谐波转矩影响较小,而减载位轮对与钢轨的黏着系数受谐波转矩影响较大。
参考文献:
[1]王祥桁,史文华,高景德,等. 交流励磁电机的谐波分析[J]. 电机与控制学报,1997,1(1):22-26.
[2]黄泽好,吴晓宇,陈哲明. 高速列车异步牵引电机谐波转矩的分析与计[J]. 重庆理工大学学报(自然科学),2013,27(8):1-5.
[3]杨顺昌,廖勇,余渝. 考虑谐波影响交流励磁电动机的电磁转矩的分析与计算[J]. 电工技术学报,2003,18(1):5-9.
[4]李伟,韩力. 逆变器供电的感应电动势谐波转矩分析与计算[J]. 微特电机,2005,(4):7-9.
[5]赵怀耘,刘建新,翟婉明. 异步牵引电机谐波转矩对机车动力学的影响[J]. 西南交通大学学报,2009,44(2):269-272.
[6]徐坤,曾京,祁亚运,等. 牵引电机谐波转矩对高速动车动力学性能的影响[J]. 振动与冲击,2018,37(19):153-158.
[7]翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京:科学出版社,2015.
[8]Z. G. Chen,W. M. Zhai,K. Y. Wang. A locomotive-track coupled vertical dynamics model with gear transmissions[J]. Vehicle System Dynamics,2017,55(2):244-267.
[9]Z. G. Chen,W. M. Zhai,K. Y. Wang. Dynamic investigation of a locomotive with effect of gear transmissions under tractive conditions[J]. Journal of Sound and Vibration,2017(408):220-233.
[10]Z. G. Chen,Z. W. Zhou,W. M. Zhai,et al. Improved analytical calculation model of spur gear mesh excitations with tooth pro?le deviations[J]. Mechanism and Machine Theory,2020(149):103838.
[11]赵怀耘. 轮对空心轴架悬机车驱动系统动力学研究[D]. 成都:西南交通大学,2010.
收稿日期:2022-05-27
基金项目:国家自然科学基金(52022083)
作者简介:金潇(1994-),男,河南商丘人,硕士研究生,工程师,主要研究方向为车辆结构强度与疲劳分析,E-mail:jinxiao930622@163.com。*通讯作者:周子伟(1995-),男,重庆人,博士研究生,主要研究方向为轨道车辆牵引传动系统动力学,E-mail:tboweiwer@163.com。

