3-UCU并联驱动式下肢外骨骼机构运动学分析

陈铸　李恒

摘要：设计了一款并联驱动式下肢外骨骼机构，髋关节采用3-UCU型并联机构，膝关节采用UCU-R型并联机构，踝关节为欠驱动球铰机构，计算出机构自由度并进行奇异性分析，机构在工作空间内不存在正、逆解奇异。采用多体系统理论对外骨骼机构进行运动分析，推导出同一坐标系下各部件上任意参考点的相对位置计算方法，建立机构位姿正逆解数学模型，借助MATLAB软件对外骨骼并联机构的工作空间和驱动轴行程进行了数学编程仿真分析，结果显示，机构工作空间形状紧凑连续，没有明显空洞，因此该机构工作性能良好。采用PSO算法进行位姿正解，验证了正、逆解算法的结果一致性。

关键词：3-UCU；并联驱动；下肢外骨骼；运动学；奇异性；工作空间；PSO算法

中图分类号：TH112 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.03.011

文章编号：1006-0316 （2023） 03-0072-09

Kinematic Analysis of 3-UCU Parallel Driven Lower Limb Exoskeleton Mechanism

CHEN Zhu，LI Heng

（ School of Mechanical Engineering， Sichuan University， Chengdu 610065， China ）

Abstract：A parallel driven lower limb exoskeleton mechanism is designed by using 3-UCU parallel mechanism for the hip joint， UCU-R parallel mechanism for the knee joint ， and underactuated spherical joint mechanism for the ankle joint. The degree of freedom of the mechanism is calculated and the singularity is analyzed. There is no forward and inverse singularity in the workspace. The multi-body system theory is used to analyze the motion of exoskeleton mechanism， and the relative position calculation method is adopted to derive any reference point on each component in the same coordinate system. The forward and inverse mathematical model of the mechanism is established. The mathematical programming simulation analysis of the workspace and the drive shaft stroke of exoskeleton parallel mechanism is carried out by using MATLAB software. The results show that the shape of the workspace of the mechanism is compact and continuous without obvious cavity， so the mechanism has good working ability. PSO algorithm is applied to the position forward solution， and the consistency of the results of the forward and inverse solution algorithm is verified.

Key words：3-UCU；parallel driven；lower limb exoskeleton；kinematic；singularity；workspace；PSO algorithm

外骨骼机器人是一种适应人体运动状态的可穿戴式机器人，常用以增强人体运动体能、提供运动防护、帮助老弱残障人士顺利行走、辅助康复训练以及负重搬运操作等[1]。外骨骼机器人的关节机构及驱动方式，决定其运动形式和性能、控制方式及策略，是研究过程中需要首先解决的关键问题之一[2]。并联机构具有结构刚度大、动力性能好、输出精度高、自重负荷比小、控制容易等优点，将并联机构应用到外骨骼机器人的结构设计中具有较好的实用优势和发展潜力，也可与串联机器人互补，扩展外骨骼机器人的应用场景[3-4]。

机构位姿正逆解是外骨骼机构运动控制的研究基础。并联机构位姿逆解相对容易，而正解通常为非线性问题，求解难度较大，可采用数值优化方法对机构位姿正解进行研究。优化方法将非线性方程组的求解转化为优化问题求解，主要有神经网络法[5]、遗传算法[6]和粒子群算法[7]。其中优化算法理论上可以根据机构的约束关系得到并联机构的全部位置正解，但对算法设计和计算机有一定要求。

通過对机构位姿正解可求得机构的工作空间，用于分析机构工作灵活性、确定驱动部件行程范围、避开机构奇异形位等[12-14]。并联机构的工作空间相比同行程的串联机构较小，常采用数值法求解，在一定精度范围内可作为设计参考。

对并联机构进行位姿正逆解，需先建立机构运动的数学模型，便于机构描述和计算，此处机构运动学建模方法采用多体系统理论。多体系统是由多个刚体或柔体通过某种方式连接而成的机械系统，在多体系统中根据拓扑结构将任一个体通过低序体阵列追溯到惯性参考系中，得到它在惯性参考坐标系中的位置和运动关系[8]。大量实践证明，多体系统理论能较为全面综合地对复杂机械系统进行运动分析[9]。

1 建模理论

采用经典的多体系统理论建立外骨骼机构的综合运动学模型。根据所设计的外骨骼结构空间形状与几何尺寸关系，建立用于全局参考的基准坐标系和局部坐标系。基准坐标系建立在相对人体骨盆静止的部件上，局部坐标系建立在其他可独立运动的部件上。在各运动部件上依次建立基准及局部坐标系S1、S2、S3、S4，其原点为运动部件上关节球心初始位置，采用右手笛卡尔坐标系，且初始位置各局部坐标系三个坐标轴方向与基准坐标系的对应坐标轴方向一致。

多体系统中相邻个体之间的局部坐标系变换使用Denavit-Hartenberg齐次变换矩阵描述，局部坐标系中的位置和方向关系均可通过坐标变换矩阵转化为基准坐标系S1中的相应关系。多体系统中的变换矩阵包括理想位置变换矩阵 、位置误差变换矩阵 、理想运动变换矩阵 以及运动误差变换矩阵 ，则坐标系Si到坐标系Sj的变换矩阵可以表示为：

式中，每个矩阵都可以由基本的运动变换矩阵或误差矩阵得到。

根据基本运动变换矩阵可知，若坐标系Si先沿X轴平移距离x，再沿Y轴平移距离y，最后沿Z轴平移距离z，按先绕Z轴、再绕Y轴、最后绕X轴的顺序分别旋转 、 、 角度得到坐标系Sj，则Si到Sj的平移旋转综合变换矩阵为：

式中：c为cos；s为sin。

系统中个体Bi沿着低序体Bj的特定坐标轴方向做平移运动时，其在各軸方向上的实际位移与理想位移存在三个轴方向上的位置误差 、 、 ，同时还存在绕三个轴旋转的角度误差 、 、 ；以及制造安装的精度导致装配完成后存在位置误差 、 、 ，垂直度误差 、 、 ，相邻个体部件装配完成的坐标系原点距离Sx、Sy、Sz，在建模时将垂直度误差当做转角误差元素处理。将以上误差代入基本运动变换矩阵中，并近似取cos ＝1、sin ＝ ，忽略 高阶无穷小量，得到B2沿着B1运动时的4个变换矩阵如式（3）～（6）所示。

式中： 、 为肢体末端固定参考点位置齐次向量； 为 转换为基准坐标系下理论位置齐次向量； 为 转换为基准坐标系下实际位置齐次向量；齐次向量末元素1参与矩阵计算；n为肢体运动部件数；i＝1， 2， …， n－1。

2 外骨骼机构运动学模型

2.1 机构描述

根据人体骨骼结构和运动特性，可将单腿骨骼简化为SRS型连杆机构（SRS表示由2个球副S和1个转动副R按字母顺序串联而成的运动链），分别对应髋关节球面副3个旋转自由度[16]、膝关节转动副1个旋转自由度、踝关节球面副3个旋转自由度，单边下肢一共7个自由度。双下肢结构左右对称，如图1所示。

为保证随人体运动的灵活性，外骨骼机构自由度应不小于人体骨骼自由度。以股骨运动为例，骨盆为机架，股骨绕髋关节球心作一定范围内的3自由度旋转运动，由于人体肌肉等软组织干涉限制，外骨骼机构的关节无法与人体骨骼关节球心重合，股骨固定部件需相对骨盆固定部件有空间6自由度，才能满足协调随动需求。理想简化情况下膝关节只有一个旋转自由度，可使外骨骼膝关节轴线与其共线，即可满足随动需求。根据以上思路设计了下肢外骨骼机构简图，如图2所示[10]，其中髋板连接外骨骼骨盆环与人体骨盆相对固定，作为机架，髋板与股骨板之间为3-UCU型并联机构（UCU表示由2个虎克铰U副和1个圆柱C副按字母顺序串联而成的运动链），提供5个旋转自由度和1个直线自由度，易知股骨板相对髋板有6个空间自由度。并联UCU链为冗余约束，可任意扩展数量或位置而不增加股骨板的自由度，便于布置驱动轴。股骨板与胫骨板之间为UCU-R型并联机构（即1个UCU链和1个R副并联），胫骨板相对股骨板有1个旋转自由度。胫骨板与鞋板之间通过球铰连接，有3个旋转自由度，由于踝关节运动幅度和机构布置空间较小，采用欠驱动关节，鞋板随足部运动时仅保证鞋板支撑面与足底平行，以满足直立行走等大部分运动情况下的支撑需求。根据修正G-K（Grubler-Kutzbach，格鲁布利尔准则与库兹贝奇准则）公式计算为[17]：

式中：F为下肢外骨骼机构的自由度；d为机构阶数；n为构件总数；g为运动副总数； 为第i个运动副的自由度数；v为机构中并联冗余约束； 为机构局部自由度。

已知：d＝6，n＝8，g＝14， ＝28，v＝24，ζ＝0。

计算得：F＝10。

即，整个下肢外骨骼机构需要10个原动驱动轴才能完全确定机构姿态。

而此处踝关节为欠驱动关节，则需股骨板和胫骨板上共7个驱动轴。

2.2 坐标系建立

以人体髋关节球心连线中点为坐标原点，直立状态下，竖直向上为z轴方向、水平向人体右侧为x轴方向、水平向前为y轴方向建立骨盆基准坐标系S1。右股骨坐标系S2原点在股骨头球心、右胫骨坐标系S3原点在膝关节球心（膝关节运动简化为单旋转运动）、右足坐标系S4原点在踝关节球心。类似地有左股骨坐标系S2L、左胫骨坐标系S3L、左足坐标系S4L。

理想穿戴情况下，外骨骼髋板部件与人体骨盆相对位置固定，外骨骼基准坐标系Sp与人体骨盆坐标系S1重合。根据零部件结构形状，右髋板坐标系SHip原点在髋板关节球心，右股骨板坐标系SThigh原点在股骨板头关节球心，右胫骨板坐标系STibia原点在胫骨板头关节球心，右鞋板坐标系SShoe原点在鞋头关节球心。类似地有左肢部件坐标系SHipL、SThighL、STibiaL、SShoeL。根据零部件尺寸、装配关系和人体运动关节确定外骨骼各机构局部坐标系的转换矩阵[13-15]。如图3、图4所示。

2.3 参考点与驱动轴长度

为描述股骨板运动状态并假定其与人体股骨运动状态一致以便计算并联驱动轴的长度，先选定股骨板上一参考点P，可令其位于股骨板上靠近膝关节固定环位置。参考点在股骨坐标系中的位置 由股骨板固定。根据股骨绕骨盆旋转的角度 、 、 和股骨头球心在骨盆坐标系中的位置 ，可得：

式中： 为参考点在骨盆坐标系中的位置。

股骨板与骨盆之间3个直线驱动轴 、 、 （下标ABC表示并联的不同轴），在骨盆上连接端点 ＝ 、 ＝ 、 ＝ ，其中 、 表示 与S1、Sp部件连接点。在股骨板上连接端点 ＝ － 、 ＝ － 、 ＝ － ，其中 为 与SThigh部件连接点距离、 为S2与SThigh原点距离， 、 可在初始状态下由股骨板结构尺寸和股骨板头与髋关节距离测得，转换到同一坐标系下计算驱动轴长度，为：

同理，胫骨板与股骨板之间1个直线驱动轴 ，在股骨板固定环上连接端点 ＝ － ，在胫骨板上连接端点 ＝ ，在同一坐标系下计算驱动轴长度，为：

2.4 机构驱动轴逆解

外骨骼机构的位姿逆解即根据人体下肢各关节运动角度 、 、 （i＝1， 2， 3，j＝i＋1）和人体与机构尺寸关系，求得人体运动转换矩阵及各关节空间位置，进而求得机构各驱动轴定位数值的过程。反之，通过机构各驱动轴直线或旋转行程求得人体下肢各关节运动角度的过程为位姿正解。

由于参考点通过连接件与人体骨骼在骨骼关节坐标系中相对位置固定，人体骨骼正常状态下只相对人体关节转动而不会相对参考点转动，在参考点位置固定时，人体骨骼理论上只能以人体关节球心与参考点连线为轴线旋转，在实际情况下由于人体骨骼、肌肉生理构造与外骨骼关节部件的运动干涉，这种旋转运动范围很小且阻力臂较大，可以作为欠约束的冗余自由度，由人体关节或其他不承受主要负载的运动副约束[11]。则参考点位置与参考点连接件相对肢体部件的三维角度，可以是由人体运动约束确定的完全映射关系，只需通过3个驱动轴定位数值确定参考点位置，即可通过映射关系确定参考点连接件的3个旋转约束角度，这样就可减少自由驱动数量，减少运动状态求解的计算量。

实际机构中，外骨骼的髋板部件和骨盆环与人体骨盆相对位置固定，外骨骼骨盆环坐标系与人体骨盆基准坐标系重合，右侧下肢关节机构驱动轴逆解方程为：

式中：af、bt、gm为对于特定人体的映射关系。

式（13）左边为各驱动轴直线及角度位置。由于股骨板、肱骨板参考点的旋转约束角度 、 、 是通过3个驱动轴确定的映射关系，则af、bt、gm可通过实验采集作为初始参数。

2.5 机构奇异性分析

机构的奇异位形是指在运动过程中出现极限点、死点、增加或失去自由度等导致机构不稳定或失去控制的情况，当机构处于奇异形位时速度反解不存在，且其对应的雅可比矩阵行列式为0。以髋关节3-UCU并联机构为例，有式（14）。

式中： 为以人体关节转角表示的末端执行广义速度； 为各并联支链驱动轴伸缩速度；J为机构末端执行速度对各支链驱动轴速度的一阶影响系数矩阵，即雅可比矩阵； 和 分别为机构的逆、正雅可比矩阵。

根据机构雅克比矩阵的奇异性，可将并联机构奇异位形分为三类[18]：

式中： 、 、 、 、 、 分别为3个驱动轴两端点在关节坐标系中初始位置向量； 为旋转位移矩阵。 ～ 表示根据式（18）分离 后的未知矩阵元素。

可以看出，机构的逆雅可比矩阵的行列式不可能为0，故需以正雅可比矩阵为基础分析机构的奇异位形[19]。由于正雅克比矩阵的解析解比较复杂，采用迭代优化法求机构驱动轴行程范围内的所有位姿数值正解，见3.2节，进而通过同一位姿的不同速度取值解得正雅克比矩阵J2各项元素数值解，速度取值以L和X的微分增量近似表示。计算结果显示，在机构的工作空间内，不存在相应的驱动轴长度L和位姿X能够满足det（J2）≤10-5。因此，该机构在工作空间内不存在正解奇异。

3 测量尺寸与仿真实验

上一节公式中可通过结构尺寸测得的数据，及可假定的人体和装配参数，如表1所示。

根据实验测得各驱动轴 、 、 、 、 、 值，可绘制各个关节运动取值点的映射空间，映射关系也可由机构运动学逆解得出。

3.1 逆解仿真与驱动轴行程范围

已知3-UCU并联机构的结构参数和末端执行器的位姿 ，求解各驱动轴长度 ，即为运动学逆解，其数学模型为：

根据人体髋关节运动限制给定取值范围为 ∈[-20°， 110°]、 ∈[-60°， 20°]、 ∈[-20°， 20°]， 、 值变化时，分别确定 、 、 的边界取值，以右下肢髋关节为例，插值拟合得理想末端工作空间形状如图5所示。

根据 、 、 的取值和式（19）、式（20），在MATLAB软件中遍历计算各驱动轴的长度逆解值，其部分结果如表2所示。驱动轴行程范围的三维空间形状如图6所示。

3.2 正解仿真与机构工作空间

已知3-UCU并联机构的结构参数和驱动轴长度 ，求解末端执行器的位姿 ，即為运动学正解，其数学模型为：

式中： 为位姿X的多维非线性函数。

可根据多维函数优化求解的思想，采用PSO（Particle Swarm Optimization，粒子群优化算法）[21]，通过MATLAB迭代计算位置正解数值解[22]。

PSO算法通过初始化一群随机粒子，然后迭代优化找到全局最优解。在每一次迭代中，粒子通过跟踪共享个体最优解pBest和种群全局最优解gBest的信息来更新粒子。PSO算法具有收敛速度快、参数少、简单易实现的优点，对高维优化问题相比遗传算法收敛速度更快。

在MATLAB中编程计算得部分结果如图7所示，可见适应度在50次迭代内达到收敛水平，多次计算验证均可达到收敛，具有较好稳定性。图8显示了相应的粒子群运动遗迹图，可见粒子逐渐汇集到目标位姿X附近（图中蓝色密集区域）。

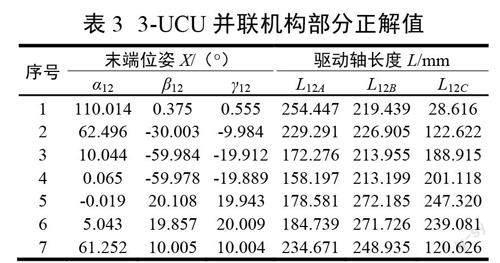
根据表2所计算的驱动轴长度逆解值，采用PSO算法正解其位姿结果如表3所示。对比可见，除了工作空间边界较远处正解位姿误差较大外，其他位姿正逆解角度误差均在0.5°之内，考虑到数值取舍和计算误差，可认为PSO算法正解3-UCU并联机构位姿具有较好的计算效率和精度。

由3.1节逆解所得的驱动轴行程范围，确定驱动轴机械设计的行程为 ∈[120， 260]、 ∈[200， 260]、 ∈[30， 300]，在MATLAB中遍历计算位姿正解值，最终得到机构的设计工作空间，如图9所示。

对比图9和图5可见，机构的设计工作空间与理想工作空间基本一致，即机构正解算法和逆解算法结果具有较好一致性。

4 总结

采用UCU型机构作为基本驱动轴部件设计了一款并联驱动式下肢外骨骼机构，采用多体系统理论对外骨骼机构进行运动分析，并建立数学模型，推导出同一坐标系下各部件上任意参考点的相对位置计算方法。

借助MATLAB软件对外骨骼并联机构的工作空间和驱动轴行程进行了数学编程仿真分析，结果显示，机构工作空间形状紧凑连续，没有明显空洞，因此该机构工作性能良好。

基于多体系统运动转换矩阵和PSO算法对机构位姿正逆解进行数值求解，为并联驱动下肢外骨骼机构的运动学分析、位姿仿真、优化设计以及下一步的运动控制研究奠定了基础，也为开发新型外骨骼机械结构积累了一定设计经验。

参考文献：

[1]YAN T，CEMPINI M，ODDO C M，et al. Review of assistive strategies in powered lower-limb orthoses and exoskeletons[J]. Robotics and Autonomous Systems，2015（64）：120-136.

[2]汪步云，王月朋，梁艺，等. 下肢外骨骼助力机器人关节驱动设计及试验分析[J]. 机械工程学报，2019，55（23）：55-66.

[3]陈学生，陈在礼，孔民秀. 并联机器人研究的进展与现状[J]. 机器人，2002，24（5）：464-470.

[4]黄真. 并联机器人机构学理论及控制[M]．北京：机械工业出版社，1997.

[5]GENG Z，HAYNES L. Neural network solution for the forward kinematics problem of a Stewart platform[C]. Robotics and Automation，1991. Proceedings，1991 IEEE International Conference on. IEEE，1991：2650-2655.

[6]BOUDREAU R，TURKKAN N. Solving the forward kinematics of parallel manipulators with a genetic algorithm[J]. Journal of  Robotic Systems，1996，13（2）：111-125.

[7]车林仙. 4-RUPaR并联机器人机构及其运动学分析[J]. 机械工程学报，2010，46（3）：35-41.

[8]休斯敦RL，刘又午. 多体系统动力学[M]. 天津：天津大学出版社，1991.

[9]刘又午. 多体动力学的休斯敦方法及其发展[J]. 中国机械工程，2000，11（6）：601-607.

[10]张策. 机械原理与机械设计[M]. 北京：机械工业出版社，2004.

[11]王焕定，章梓茂，景瑞. 结构力学[M]. 北京：高等教育出版社，2010.

[12]John J. Craig. Introduction to Robotics：Mechanics and Control [M]. Third Edition. Beijing：China Machine Press，2005：19-128.

[13]蔡自兴，谢斌. 机器人学[M]. 3版. 北京：清华大学出版社，2015：19-60.

[14]张福学. 机器人技术及其应用[M]. 北京：电子工业出版社，2000.

[15]史小华，王洪波，孙利，等. 外骨骼型下肢康复机器人结构设计与动力学分析[J]. 机械工程学报，2014，50（3）：41-48.

[16]陈占伏，杨秀霞，顾文锦. 下肢外骨骼机械结构的分析与设计[J]. 计算机仿真，2008，25（8）：238-241，334.

[17]陈伟海，徐颖俊，王建华，等. 并联式下肢康复外骨骼运动学及工作空间分析[J]. 机械工程学报，2015，51（13）：158-166.

[18]曹永刚，张玉茹. 6-RSS型并联机构奇异性分析[J]. 机械工程学报，2008，44（6）：79-87.

[19]叶增林，张良安，陈华，等. 2URR-SRR-RUPUR并聯式腿部康复机器人机构设计与运动性能分析[J]. 机械传动，2021，45（3）：82-89.

[20]徐化娟，李宏伟，张春燕. 一种新型3T1R并联机器人机构运动学分析与参数优化[J]. 机械传动，2021，45（5）：57-65.

[21]Kennedy J . Particle swarm optimization[J]. Proc. of 1995 IEEE Int. Conf. Neural Networks，（Perth，Australia），2011，4（8）：1942-1948.

[22]王启明，苏建，隋振，等. 一种新型冗余驱动并联机构位姿正解研究[J]. 机械工程学报，2019，55（9）：40-47.

收稿日期：2022-09-28

作者简介：陈铸（1999－），男，四川达州人，硕士研究生，主要研究方向为数字化设计与制造，E-mail：2020223025146@stu.scu.edu.cn；李恒（1998－），男，安徽六安人，硕士研究生，主要研究方向为机械电子工程，E-mail：2020223020033@stu.scu.edu.cn。