离心式喷嘴结构参数的多目标优化设计

盛 鑫，侯 力，游云霞，彭真臻

（四川大学机械工程学院，四川成都 610065）

1 引言

航空燃油喷嘴的喷雾形态、雾化锥角、液滴尺寸、出口流量等雾化性能对燃烧稳定性、启动点火可靠性、污染物排放等有着较大影响。大量试验表明：喷嘴的结构参数对雾化性能有很大的影响［1−2］，因此，对喷嘴的结构参数进行优化设计有重要的意义。

常用的喷嘴按其工作原理分类，主要有旋流式压力喷嘴（离心喷嘴）、旋转喷嘴、喷气喷嘴等。离心喷嘴由于拥有结构简单、雾化质量高、性能稳定等优点，被广泛用于各种飞机发动机和燃气轮机中［3−5］。文献［6］利用数值仿真得到了喷嘴孔径等结构参数对雾化锥角和流量系数的影响，结果表明：旋流室长度增加会导致雾化锥角增大；文献［7−8］通过试验给出了喷嘴结构参数对雾化锥角的影响及流量的分布特性，并通过拟合得到了关于雾化锥角和流量系数的表达式；文献［9］采用ALE 方法研究了旋流室收缩角、扩张段长度和扩张角对喷雾性能的影响，结果表明：雾化角随着收缩角的增大而减小，但随着扩张角的增大而增大；文献［10］采用VOF方法分析了离心喷嘴的旋流室直径、等直段直径、等直段长度、扩张段角度等结构参数变化对流量系数、液膜厚度及雾化锥角的影响。上述研究主要采用多次的试验和数值模拟等方法，在需要多次改变设计变量时，试验成本和计算成本较大，此外，得到的经验公式由于样本较少，有较大误差，预测分析效果较差，且没有考虑到喷嘴各结构参数对雾化性能的交叉影响。

为了考虑多个变量对雾化性能的影响，并尽可能减少试验及仿真的次数，选取扩张段长度Ld、等直段长度L0、等直段直径d0、扩张半角θ、收缩半角α为设计参数，基于验证后的数值模型，采用优化拉丁超立方抽样方法［11］进行试验设计，建立关于雾化锥角β和质量流率Q的响应面预测模型，根据得到的显示表达式，分析结构参数对雾化锥角和质量流率的影响，并求解单一目标最优时的结构参数；为达到全局最优，使用非支配排序遗传算法求得最优解集，确定使得雾化锥角和质量流率最佳的结构参数。

2 CFD数值模拟

流体流动的基本控制方程如下：

质量守恒方程：

动量守恒方程：

式中vx、vy、vz—流体沿着X、Y、Z轴的速度分量；ρ—流体密度；μ—运动粘度系数；F—微单原体的体积力；P—流体微原体上的压力。

离心式喷嘴中有燃油和空气两相，为了更好的捕捉气液分界面和每相的体积分数，便于提取雾化锥角，采用VOF方法来模拟喷嘴模型内部的流动过程，VOF的体积分数方程为：

考虑到喷嘴内部流动有较强的旋流和湍流，流体变化剧烈，因此，选择RNG k−ε湍流模型，相较于标准k−ε模型，RNG k−ε模型考虑了湍流旋涡，有更高的可信度和精度，湍动能耗散的输运方程如下：

2.1 网格划分与边界条件

双通道离心式喷嘴，主要由喷嘴壳体、旋流器、密封垫、旋流罩、节流管、滤网、支架等组成，也可以看作是两个离心式喷嘴组合而成［12］，这里主要对主通道的结构参数进行设计优化，主通道结构，如图1所示。采用ICEM对喷嘴模型进行非结构四面体网格划分，并对等直段和出口处流体变化剧烈的区域进行局部加密处理。分别采用40万、60万、80万和100万数量级的网格设置进行网格无关性验证，根据计算结果，对比出口截面处燃油的速度分布情况。

图1 喷嘴主通道结构Fig.1 Main Channel Structure of Nozzle

由图2可知，随着网格数量级从40万增加到60万时，出口速度分布结果逐渐趋于一致，当网格的数量级在80万及以上时候，出口速度的差异越来越小，最大相对误差为2.1%，此时能已经较好的反映出计算结果，计算结果不会随着网格数量的增加有较大的变化，但是当网格的数量为100万及以上时，会占用更大的计算资源，耗费更多计算成本。综合考虑，采用80万数量级的网格划分设置进行后续的数值模拟。边界条件，如图3所示。设置主项为空气，次项为航空燃油，壁面为无滑移壁面，进口条件设置为压力进口条件，根据喷嘴的实际工作要求，设置进口压力为2.1MPa，出口条件为压力出口条件。速度与压力耦合方法使用PSIO算法，其中压力插值方法为PRESTO！，动量采用二阶迎风格式，其余方程均为一阶迎风格式。

图3 网格划分及边界条件Fig.3 Grid Division and Boundary Conditions

2.2 结果及验证

为验证数值计算模型是否真实可信，对模型进行可靠性分析。以进口压力为单一变量，使用不同进口压力条件进行仿真计算，并将得到的雾化锥角的结果与试验结果比较，试验得到的雾化锥角，如图4所示。如图5所示，试验主要在燃油喷嘴雾化性能综合试验台上进行，试验台主要由工控机、燃油、空气供应系统、管路系统、摄影系统、测量系统及试验件等部分组成，将拍摄得到的图像进行降噪、提取边界等处理，得到雾化锥角的值。

图4 0.6MPa时的雾化锥角βFig.4 Spray Cone Angle β at 0.6MPa

图5 试验装置Fig.5 Experimental Device

由图6可知，数值模拟的雾化锥角值随着进口压力的增大，有小幅度增大的趋势，这与实验结果有相同的趋势。数值模拟得到的雾化锥角值比实验值要小，最大误差为2.6%，这主要是因为数值模拟中对模型进行了简化处理，省略了喷嘴的滤网、支架等部件，且实际喷嘴的加工过程中存在不可避免的误差。

图6 数值模拟值与试验值对比Fig.6 Comparison of Numerical Simulation and Experimental Value

3 喷嘴结构参数的优化设计

3.1 响应面代理模型的建立

离心喷嘴的结构设计中，需要多次改变设计参数，为了降低多次试验和CFD模拟的成本，提高优化效率，在不降低模型精度的条件下，使用高效近似数学模型代替试验或实际CFD 分析模型。常用的代理模型有响应面模型、Kriging模型、神经网络模型等，响应面模型有构建简单、计算速度快、可以得出简单的显示数学表达式等优点，故选择响应面方法构建代理计算模型。选取扩张段长度Ld、等直段长度L0、等直段直径d0、扩张半角θ、收缩半角α对喷嘴雾化性能有较大的影响的结构参数作为设计变量，参考设计要求和加工范围后，分别选取雾化锥角β、质量流率Q作为响应变量，设计变量的取值范围，如表1所示。

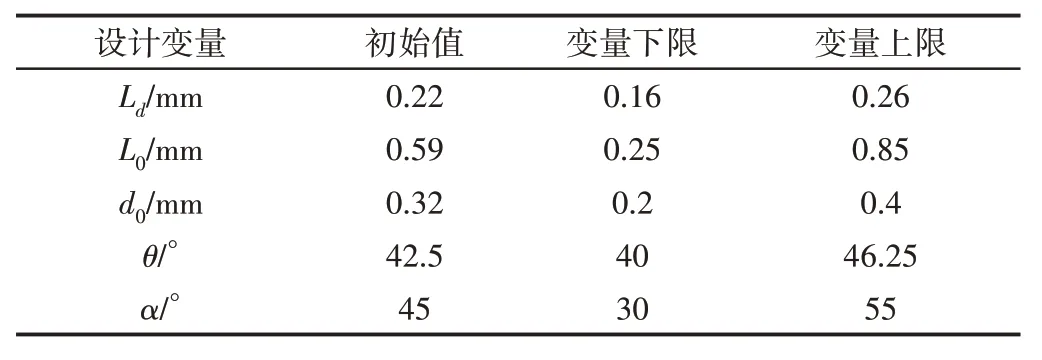
表1 设计变量的取值范围Tab.1 Value Range of Design Variables

试验设计是以概率和统计的方法为基础，从设计空间选取有限个数的样本点来反映整个设计空间的特性的方法。为了保证样本点最大可能均匀地覆盖到整个设计空间，采用优化拉丁超立方试验设计方法，生成100组设计变量的样本点，用得到的设计变量参数得到新的喷嘴三维模型，设置进口压力2.1MPa 进行CFD 模拟，获得100 组不同参数组合下的雾化锥角和质量流率值，设置其中80组为训练集，20组为测试集。为了消除样本点的量纲和奇异样本数据对代理模型精度产生的影响，对训练集和测试集所有样本点进行归一化处理，采用离差标准化方法将样本点值映射到［0，1］之间。

基于得到的训练集数据，通过Isight软件，采用RSM 四次多项式拟合分别建立关于雾化锥角和质量流率的代理模型。设置误差分析方法为交叉验证策略，并以残差平方最小为目标，使完全搜索（Exhaustive Search）进行关键项选择，选择使拟合误差最小的项，最终得到显式表达式如下：

代理模型精度，如表2所示。相关系数和修正相关系数都大于0.95，均方根误差值小，表明采用RSM方法建立的关于雾化锥角和质量流率的代理模型的全局误差小、全局逼近效果好。

表2 响应面模型的精度指标Tab.2 Precision Index of RSM

将测试集中的雾化锥角和质量流率值与代理模型得到的响应值进行比较，得到最大误差分别为2.53%和2.32%。图7可以看出残差点较好分布在直线上，符合正态分布，表明得到的模型可信度高适应性好。综合上述分析，可以认为，得到的RSM响应面代理模型有较高的可信度和可靠度，满足后续优化设计的要求。图8所示的参数贡献度图中，蓝色表示正效应，红色为负效应，图8（a）表明扩张半角和等直段直径对雾化锥角的影响最为显著，总体呈正相关。其中，扩张角对雾化锥角影响较大主要是由于喷嘴出口存在扩张角时，喷嘴的出口壁面较薄，提高了气液间的相互作用，外层喷雾速度和径向速度相较于没有扩张段时有了一定的提升，使得液膜分布的范围更广。扩张段长度、等直段长度与雾化锥角呈负相关，且相关性较小，由图8（b）可知，其中等直段直径和收缩半角对质量流率的影响最为显著，扩张段长度、扩张半角和等直段长度与质量流率均呈负相关，但相关性较小，表明这些参数对质量流率的影响很小。由图9（a）~图9（c）得出：无论等直段直径和收缩半角处于任何水平，雾化锥角都随着扩张半角的增大而增大，且变化速率越来越大。当收缩半角处于中等值域范围时，等直段直径增大，使得雾化锥角先增大后减小，随后再略有增加，收缩半角的增大使雾化锥角有较小程度减小；图9（d）分析了等直段直径和收缩半角对质量流率的交互影响作用，结果表明：当收缩半角处于较低水平时，随着等直段直径的增大，质量流率有较大幅度的变化，但收缩半角的增大导致质量流率呈下降趋势。

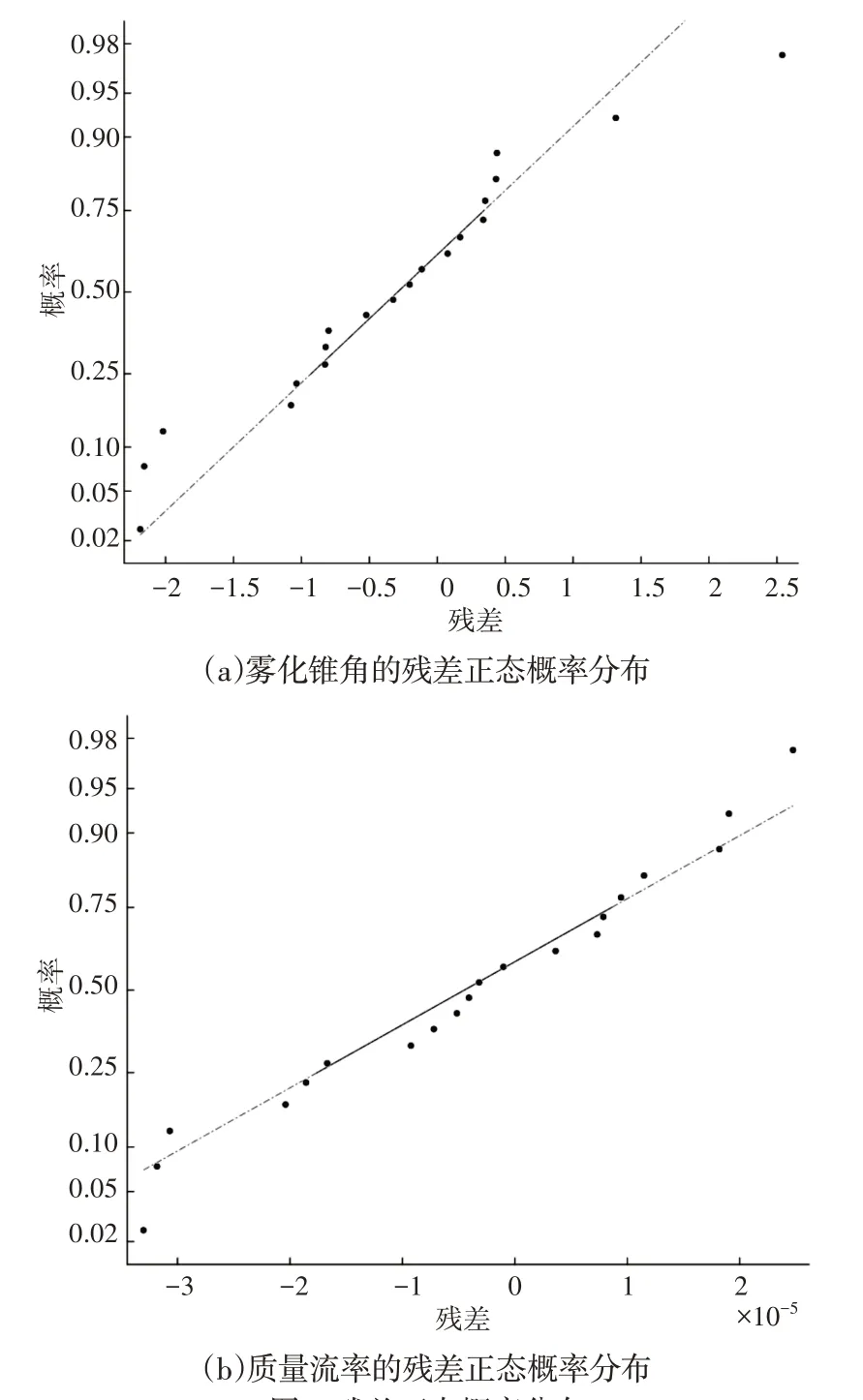
图7 残差正态概率分布Fig.7 Residual Normal Probability Distribution

图8 参数贡献度Fig.8 Contribution of Design Parameters

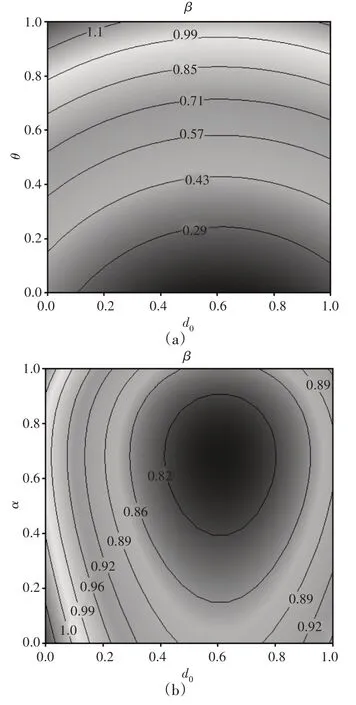
图9 交互作用响应图Fig.9 Response Map of Interaction

3.2 单目标优化

喷嘴的雾化锥角太小会使得燃油主要分布在燃烧室的中线附近，导致燃油颗粒过大使得燃烧不充分，容易冒烟；增大雾化锥角可以增大与空气的接触面，使得燃烧更充分，但是当其过大时，燃油喷射到燃烧室的壁面，会导致积碳，所以雾化锥角不宜过大或过小，在参考对应燃烧室的设计要求后确定雾化锥角的范围为［90°，100°］，同时，质量流率也是影响喷嘴性能的重要指标，它对燃烧室的输出功率和供热量大小有重要影响，质量流率过小会导致燃烧室点火性能下降，造成输出功率不稳定，严重时可致发动机停车。

因此，分别以雾化锥角和质量流率作为优化目标，以扩张段长度、直线段长度、直线段直径、扩张半角、收缩半角作为设计变量，基于自适应模拟退火算法（ASA）［13］，进行单目标优化，优化结果，如表3 所示。当以雾化锥角为最大作为优化目标时候，优化结果为99.82°，比初始模型提升了10.1%，但这时的质量流率较初始模型下降了7.8%；当以质量流率最大为优化目标时，最大为0.00162 kg/s，较初始模型提升了36.7%，但雾化锥角减少了8.8%。综上所述可知，在使用单目标优化时，其中一个目标的改善是以牺牲另一个为代价的，无法得到雾化锥角和质量流率同时达到最优的解，故接下来采用多目标优化方法进行优化设计。

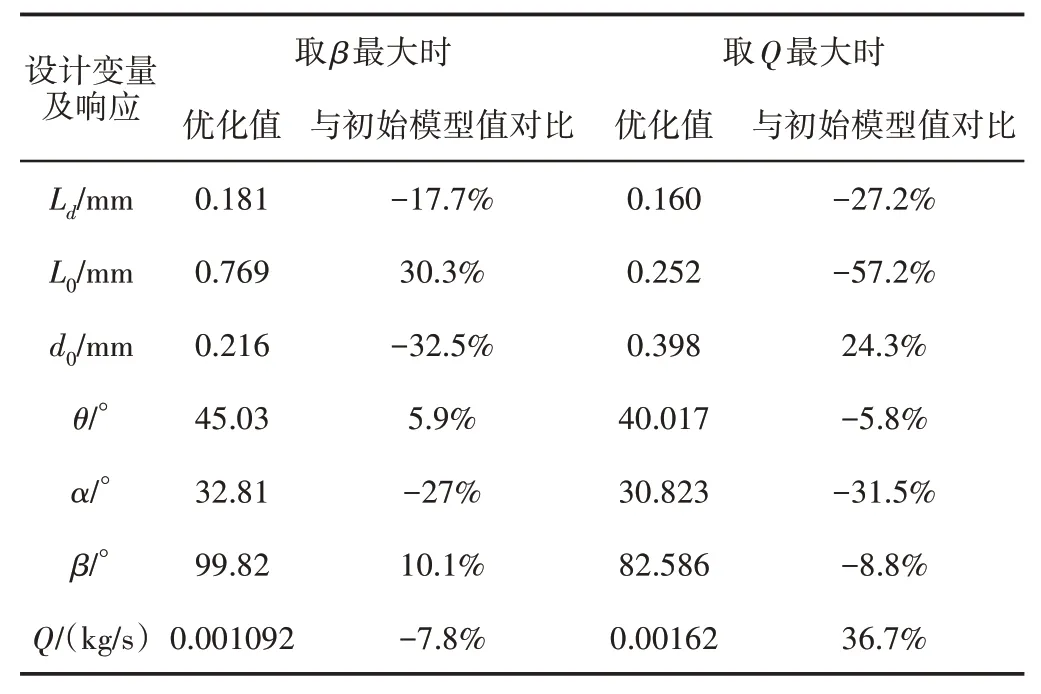
表3 单目标优化结果Tab.3 Single Objective Optimization Results

3.3 多目标优化

为了使得雾化锥角和质量流率同时达到最优，进而提升离心喷嘴的综合性能，采用非支配排序遗传算法（NSGA−Ⅱ）进行多目标优化设计，NSGA−Ⅱ算法是目前应用最广泛的进化多目标优化算法之一，由文献［14］在2000年通过对NSGA算法进行改进提出。

多目标优化的表达式，如式（8）所示。设置初始种群大小为20，交叉概率为0.8，遗传代数为200进行迭代。最终选出的4组候选优化结果，如表4所示。

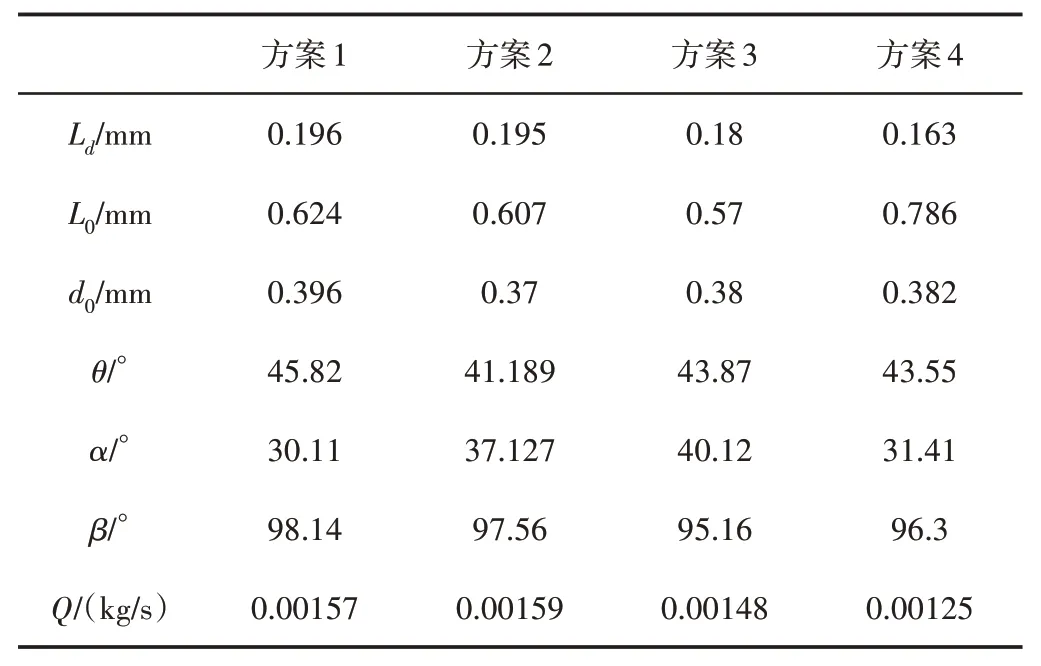
表4 候选优化结果Tab.4 Candidate Optimization Results

比较上述不同方案，综合考虑加工因素和雾化性能后，选择方案一中的结构参数作为最优参数，将优化后的离心喷嘴结构参数重新进行建模与数值仿真，x=0截面处的两相分布云图对比，如图10所示。

图10 优化前后雾化锥角对比Fig.10 Comparison of Spray Cone Angle After Optimization

将基于代理模型的优化计算结果与实际数值模拟计算结果相对比，雾化锥角的相对误差约为1.18%，质量流率的相对误差约为−1.08%，均在可接受范围之内，优化结果表明：相对于初始模型，优化模型的雾化锥角值提升了约8.3%，质量流率提升了约32.4%。

表5 优化结果与仿真值对比Tab.5 Comparison Between Optimization Results and CFD Values

4 结论

（1）影响度分析结果表明：喷嘴扩张半角、等直段直径对雾化锥角贡献程度较高，呈正相关，收缩半角、扩张段长度、等直段长度为负效应结构参数，对雾化锥角值贡献度较小；等直段直径对质量流率的影响最为显著，呈单增趋势，其次为收缩半角，随着收缩半角的增大质量流率越小；其余结构参数对质量流率的影响不大，这为后续喷嘴的结构设计提供了参考。

（2）通过单目标优化，分别得到了当雾化锥角约束条件内的最大值和质量流率最大时的结构参数，相较于原始模型，两个单项目标性能分别提升了10.1%和36.7%。

（3）为了使得喷嘴的整体雾化性能最优，使用NSGA−Ⅱ算法进行两目标优化设计，得到了使得雾化锥角和质量流率同时最优的喷嘴结构参数，当扩张段长度为0.196mm、等直段长度为0.624mm、等直段直径为0.396mm、扩张半角为45.82°、收缩半角为30.11°时，雾化锥角提升了8.3%，质量流率提升了32.4%，这表明优化后的离心喷嘴的综合雾化性能有较大的提高。