航空不锈钢编织软管压力脉动特性研究

赵龙超，李新浩，姚静，3，杨帅，张乾瑞

(1.新乡航空工业(集团)有限公司，河南新乡 453002；2.燕山大学机械工程学院，河北秦皇岛 066004；3.燕山大学河北省重型机械流体动力传输与控制重点实验室，河北秦皇岛 066004)

0 前言

压力脉动可直接造成管路产生应力脉动和机械振动[1]，进而使液压能源管路系统内流体和固体管路产生强迫振动，最终导致飞机液压系统振动[2]。如果固体管道的固有频率与流体的谐振频率相接近，或者与液压泵的脉动频率相接近，则会产生流固耦合共振[3]，将导致管路失效破裂[4]。国内外均有关于管路系统谐振所造成的管路破裂事故，因而对飞机能源管路系统的动态特性分析具有重要意义[3]。由于在泵控系统中从泵到执行机构的距离一般较长，因此其间的管道系统的影响较大[5]。软管由于其自身存在较大的弹性，在同样的长度下，对系统的影响要比钢管大许多[6]。因此分析压力脉动在软管中的传播机制对于制定相应的压力脉动抑制方法和控制策略至关重要[7]。

目前，不锈钢编织增强聚四氟乙烯软管是航空、航天领域各类液压、气动和燃油机构中的主要元件[8]，由导电的聚四氟乙烯内管和不锈钢丝编织增强层构成，具有质量轻、不需要基质就可以成为增强层等优点[9]。航空软管一般采用常规编织，此外还有菱形、大力神和三轴编织[10-14]。

近年来形成了几类管道压力传递模型的建模方法，包括电学比拟法、特征阻抗法、特征线法、分布参数法和集中参数法等。电学比拟法在实际工程中应用最广，基于该方法的供油系统软管、发电系统中的液压管路、风力发电机长管路以及水下控制模块长软管的压力传递模型都已相继被建立起来[1，6，15-16]。此外吴卫峰[17]基于特征阻抗法建立了液压管道模型。焦宗夏[3]给出了流体传输管路网络系统的特性阻抗解法，并进行了系统的动态特性仿真分析。周瑞祥等[4]利用特征线法建立了航空燃油管路模型。罗文俊等[18]建立了系统压力脉动瞬态模型，使用特征线法对系统管路中压力脉动进行仿真。在工程流体力学的基础上，高双锋[7]运用分布参数的频率方法详细研究了高压胶管的数学模型并对模型进行了适合于工程应用的简化。赵宇[5]建立软管集中参数模型，并基于模型分析了软管对系统的影响。KRUS[19]给出了软管的简化集总参数模型，进行了时间模型时域和频域仿真。除了上述经典模型以外，龚国芹[20]还建立了调功液压管路系统等效阻尼模型，提出降低软管材料弹性模量抑制脉动。

但是现有模型存在考虑不全面的问题，例如龚国芹[20]没有考虑软管中油液惯性即液感对压力脉动的影响，侯秉睿等[15]和吴卫峰[17]没有考虑软管变形对液容的影响，而李耿标[1]和高双锋[7]则是将软管当作各向同性材料而忽略了软管的各向异性以及复杂变形的结构特点。还有一些研究没有考虑压力脉动引起的软管流固耦合振动问题，此外这类研究也缺乏实验验证[3，19]。

作者建立了基于电学比拟的双编织层航空液压短软管压力传递模型，对聚四氟乙烯层和双层不锈钢编织层进行受力分析，建立了编织层本构模型计算其各向刚度，得到管各层变形与软管液容的解析解，仿真研究了编织钢丝直径、编织角度、编织股数和每股钢丝数对软管液容和软管压力传递的影响，及其对于软管共振的影响。最后通过某型飞机起落架应急放能源的软管实验验证了所建压力传递模型的准确性。

1 基于电液比拟的软管压力传递模型

某型飞机应急放能源压力影响研究中，涉及到的软管几何长度在0.35 m左右。液压泵的脉动频率1 140 Hz，计算得到的脉动波长1.09 m。本文作者所研究的系统脉动波长远大于软管长度，所以可以采用电学比拟的方法进行软管对压力传递的分析。

1.1 电学比拟模型

如图1所示，根据管道传输动力学，软管可以简化为一个感抗系统，液感和液容起到对压力脉动削峰填谷的作用。根据等效电路模型，软管输入输出压力之间的关系为

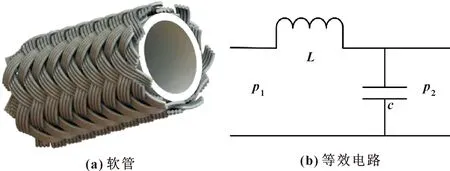
图1 软管等效电路

(1)

(2)

(3)

C=C0+CH

(4)

其中：L代表油液惯性力的影响；液容C代表单位压力变化量下流体体积的变化量。在管路中体积变化量包含两部分：一是油液压缩带来的体积变化量C0，它与管道的直径D0、长度l和油液弹性模量E0有关；另外是管道在内压作用下扩张变形带来的CH。由于不锈钢编织软管是非均匀各向异性的弹性体，目前没有准确的液容计算公式。

1.2 基于编织本构模型的软管液容计算

对两层编织层以及聚四氟乙烯层进行受力分析，由图2所示，分别受到单位长度的内压力p0D0、p1D1和p2D2与截面处的拉力T0、T1和T2，聚四氟乙烯层和编织层在这几个力的作用下达到受力平衡。

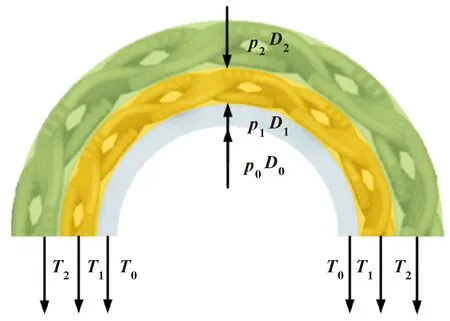
图2 双层钢丝编织聚四氟乙烯管受力分析

在如图2所示的截面内对内外层进行垂直方向的受力分析可得

p1D1+2T0=p0D0

(5)

p2D2+2T1=p1D1

(6)

p2D2=2T2

(7)

由胡克定律

(8)

(9)

(10)

其中：A0、A1、A2和l0、l1、l2分别为聚四氟乙烯层、编织层1和编织层2的抗拉刚度和环形周长。拉力、抗拉刚度和周长满足T0/T1=(Δl0l1A0)/(Δl1l0A1)，可认为Δl0/Δl1=l0/l1，故T0/T1=A0/A1。同理可得T0/T2=A0/A2，结合公式(6)(7)得到p1和p2

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

其中：H是聚四氟乙烯层的长度。液容为液体体积变化与引起它变化的压力变化之比，即C=-dV/dp，单位长度的体积变化量ΔV可由内径变化量ΔD0求得。

(19)

(20)

E1和E2分别是编织层1和编织层2的周向弹性模量，它们由筒状编织物的本构模型和坐标变换方法得到。钢丝坐标下的柔度矩阵如式(21)所示：

(21)

由于刚度矩阵是柔度矩阵的逆，所以有式(22)。

(22)

(23)

Γ=1-ν32ν23-ν12ν21-ν13ν31-ν21ν23ν13-ν31ν12ν32

(24)

(25)

由于304不锈钢材料具有各向同性，则有E1=E2=E3=E,ν12=ν21=ν13=ν31=ν23=ν32=ν。如图3所示，柔度矩阵从原始的钢丝坐标系到起伏坐标系的变换，如式(26)所示，再从起伏坐标系的柔度矩阵变换到起伏坐标系的刚度矩阵。

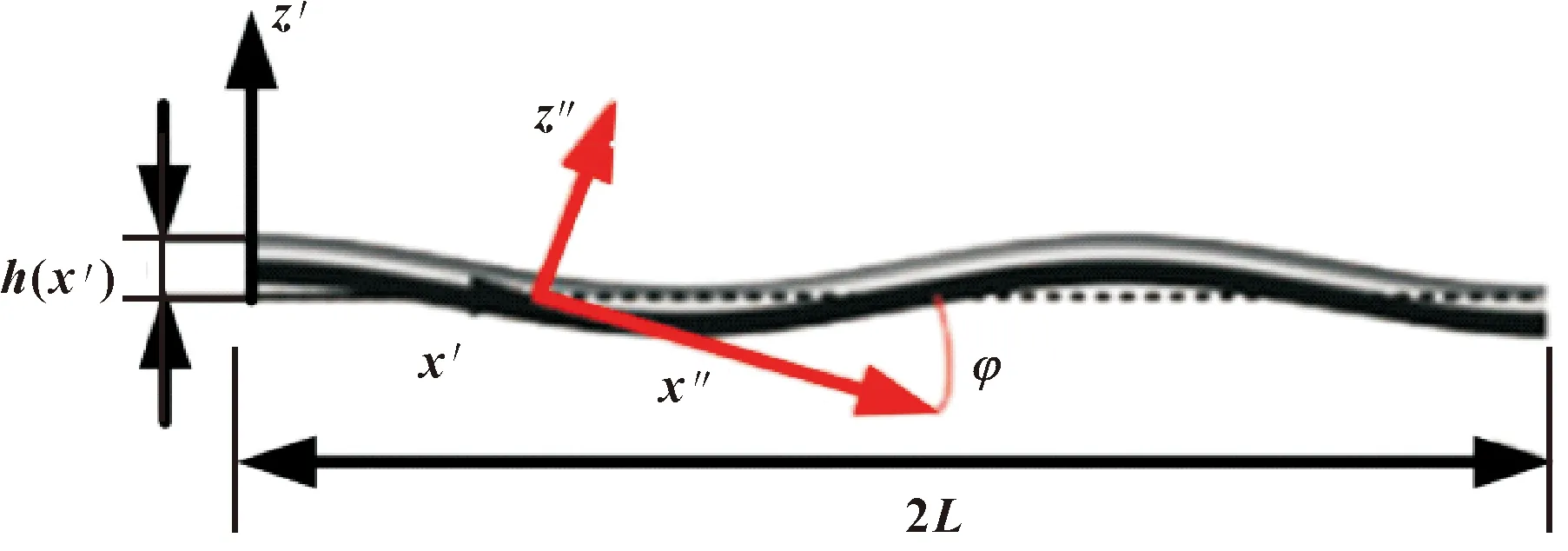
图3 钢丝坐标系(x′，y′，z′)到起伏 坐标系(x″，y″，z″)

(26)

(27)

(28)

m=cosφ

(29)

n=sinφ

(30)

(31)

(32)

(33)

式中：β为编织股之间的偏转角；r0为编织层到软管中轴的距离；N为编制股数；L为钢丝一个起伏周期长度。以上参数的几何关系可以参考图4。钢丝起伏可以视作符合正弦规律，其坐标系简图如图5所示，其方程可以由式(34)表示。从钢丝起伏坐标系到编织层轴坐标系变换由式(35)定义。

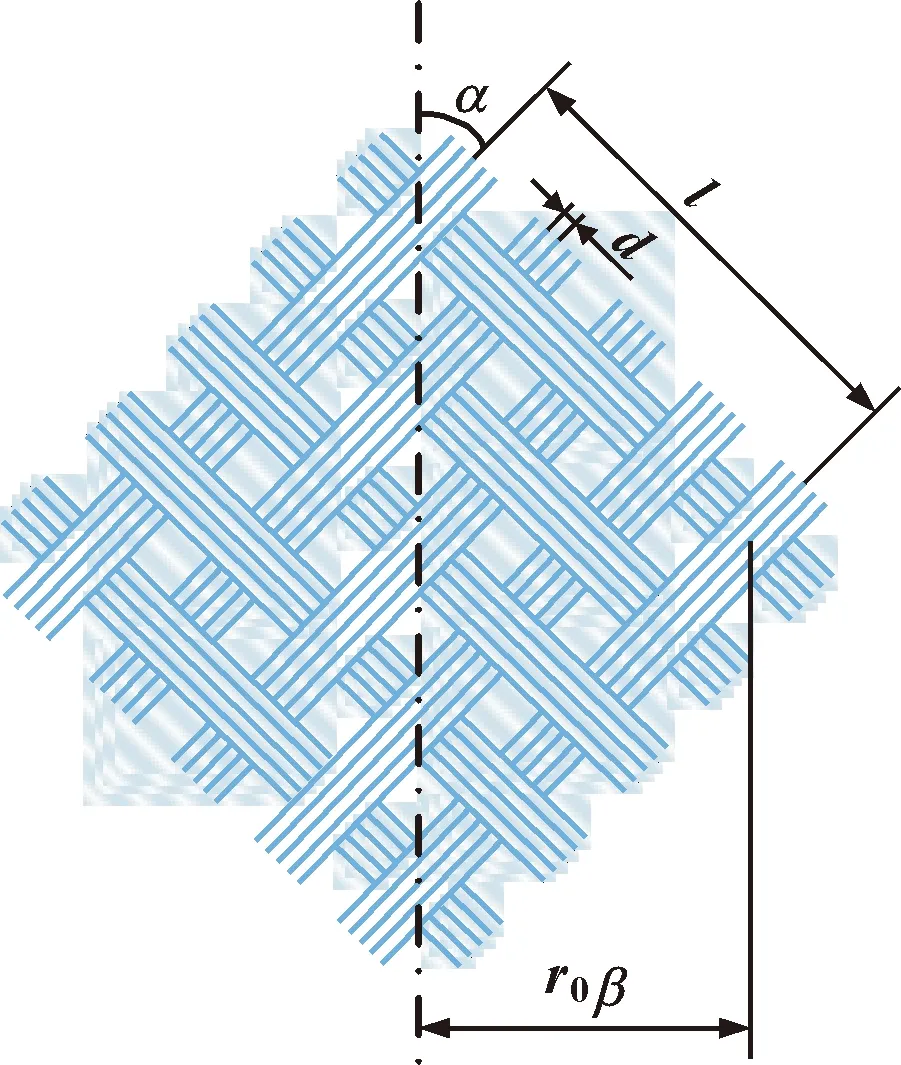
图4 编织晶胞几何形状

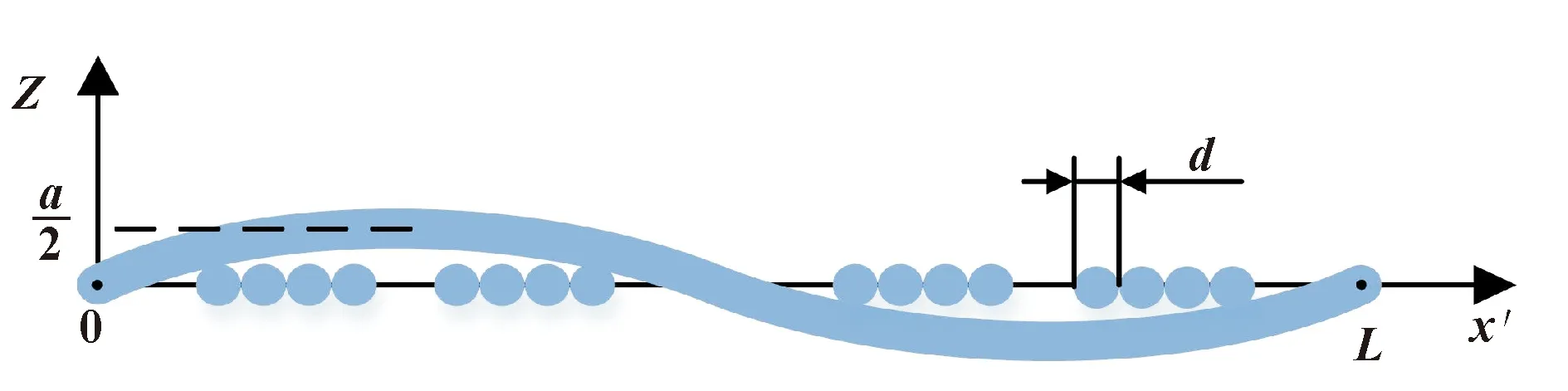
图5 钢丝起伏坐标系简图

h(x′)=asin(kx′)

(34)

Cxyz=P-1C′xyzRPR-1

(35)

(36)

c=cosθ

(37)

s=sinθ

(38)

由于编织层并不是紧密的实体，因此需要在刚度矩阵上乘以一个体积分数V，由式(39)定义。

(39)

(40)

SG=(CG)-1

(41)

(42)

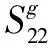
2 参数仿真模型与脉动影响因素研究

2.1 编织股数对软管液容与压力传递的影响

基于图6和图7所示的Simulink仿真模型，其他条件不变的情况下，将编织层1单方向编织股数分别设置为8、9、10、11、12，编织层2单方向编织股数分别设置为10、11、12、13、14。当增加编织股数时，液容随之减小。压力脉动抑制效果如图8所示，参考图9相比软管内的油液压缩变形，软管变形对脉动抑制效果极其有限，且编织股数的影响微不足道。

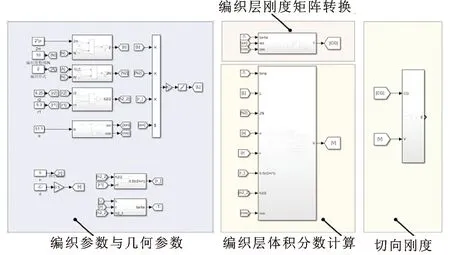
图6 编织层轴坐标下本构模型Simulink仿真模型

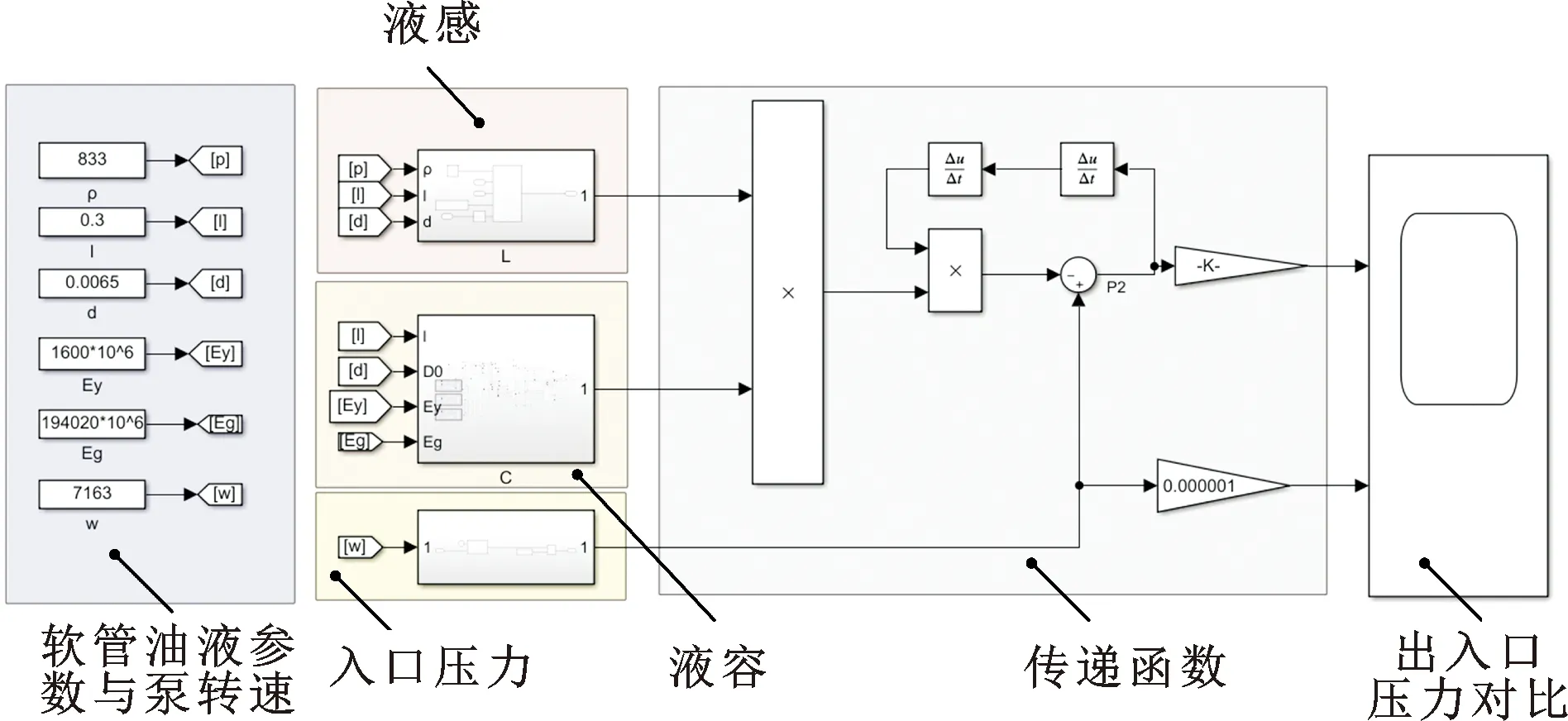
图7 软管电学比拟的压力传递Simulink仿真模型

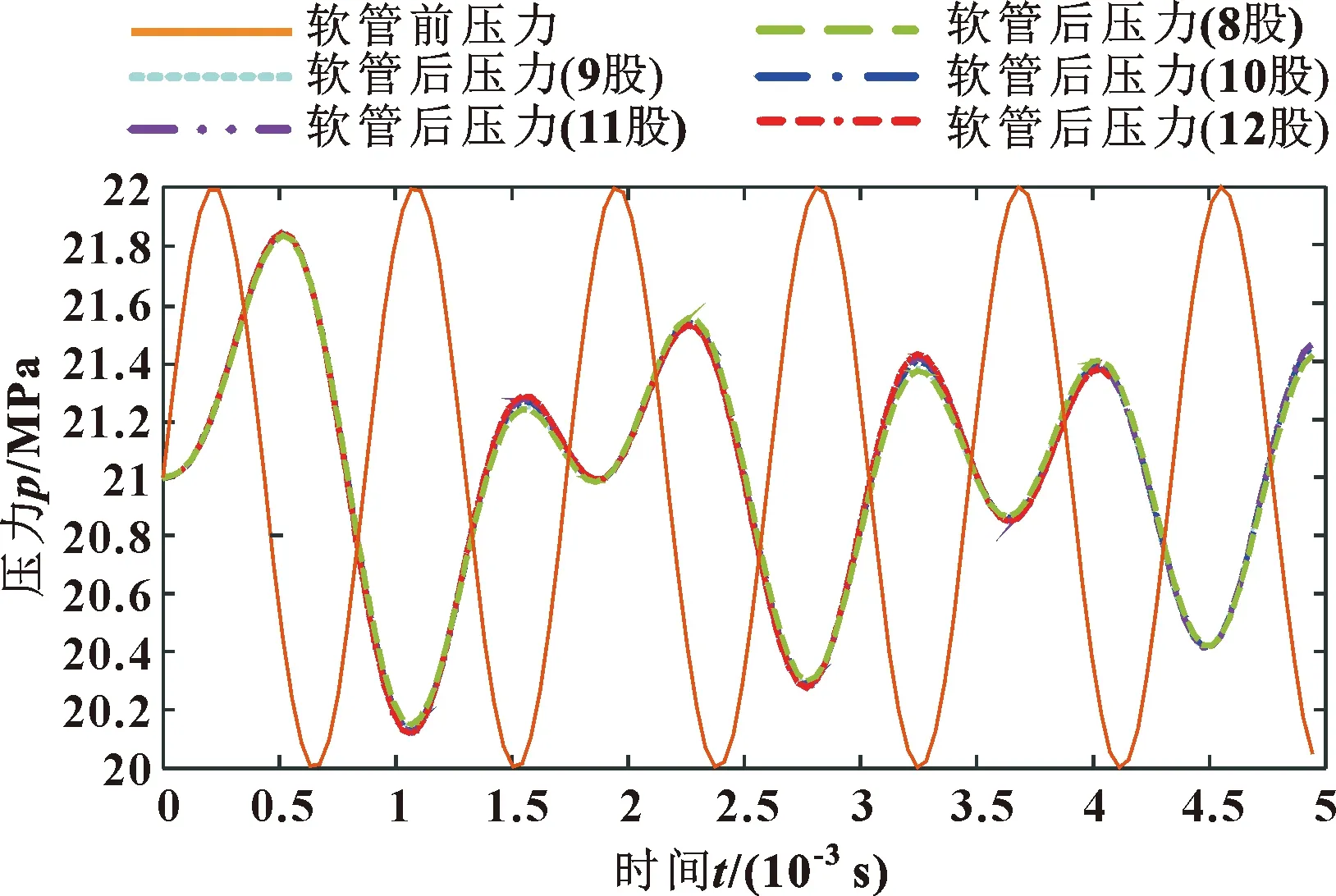
图8 不同编织股数压力脉动对比曲线

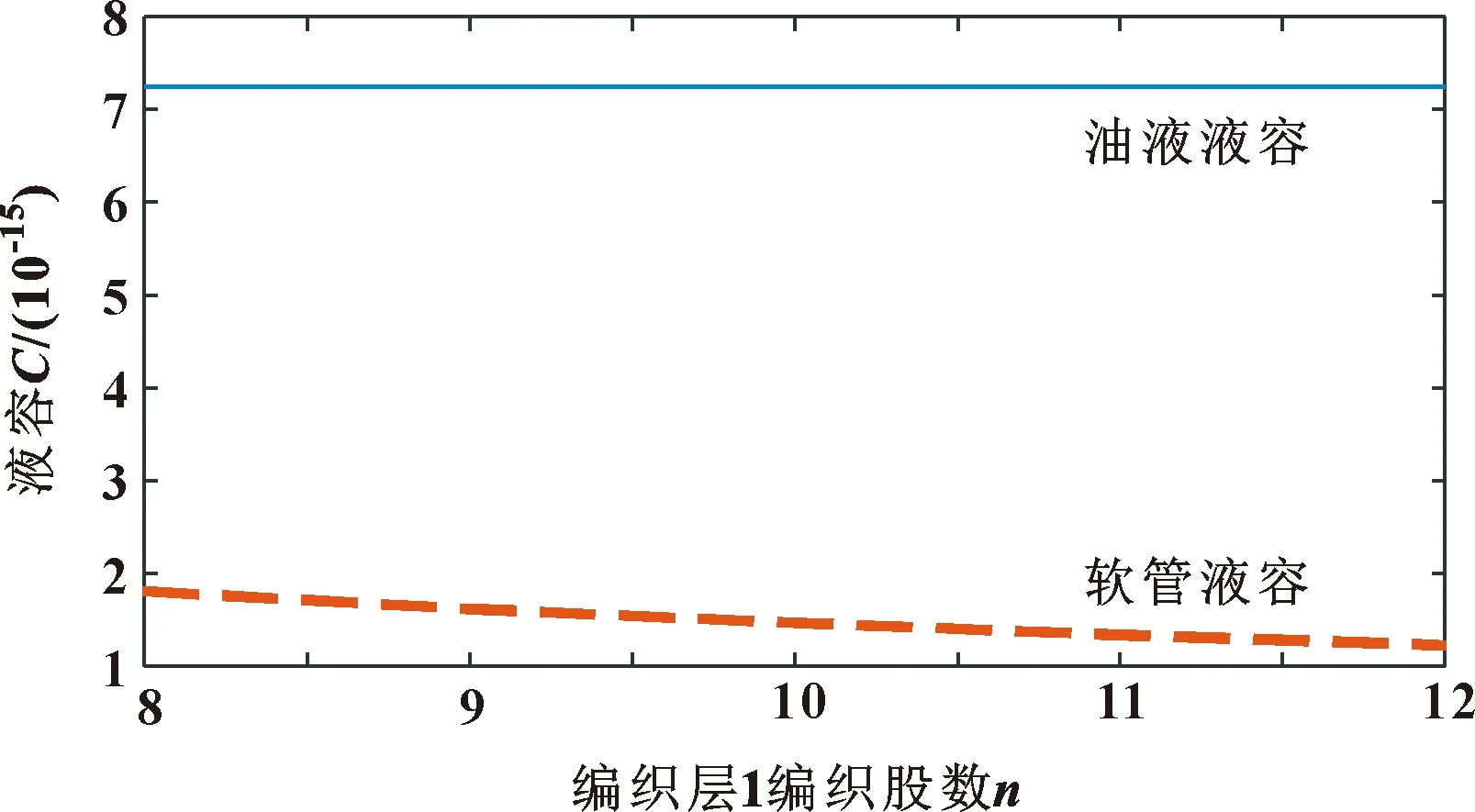
图9 不同编织股数下的软管与油液液容

2.2 编织角度对软管液容与压力传递的影响

其他条件不变的情况下，将编织角分别设置为47.1°、49.1°、51.1°、53.1°、55.1°。当编织角度增大时，压力脉动抑制效果如图10所示。可见软管通径和长度不变情况下改变编织角，软管液容减小(见图11)，但是相比软管内油液压缩变形，软管变形对脉动抑制效果依然十分有限。

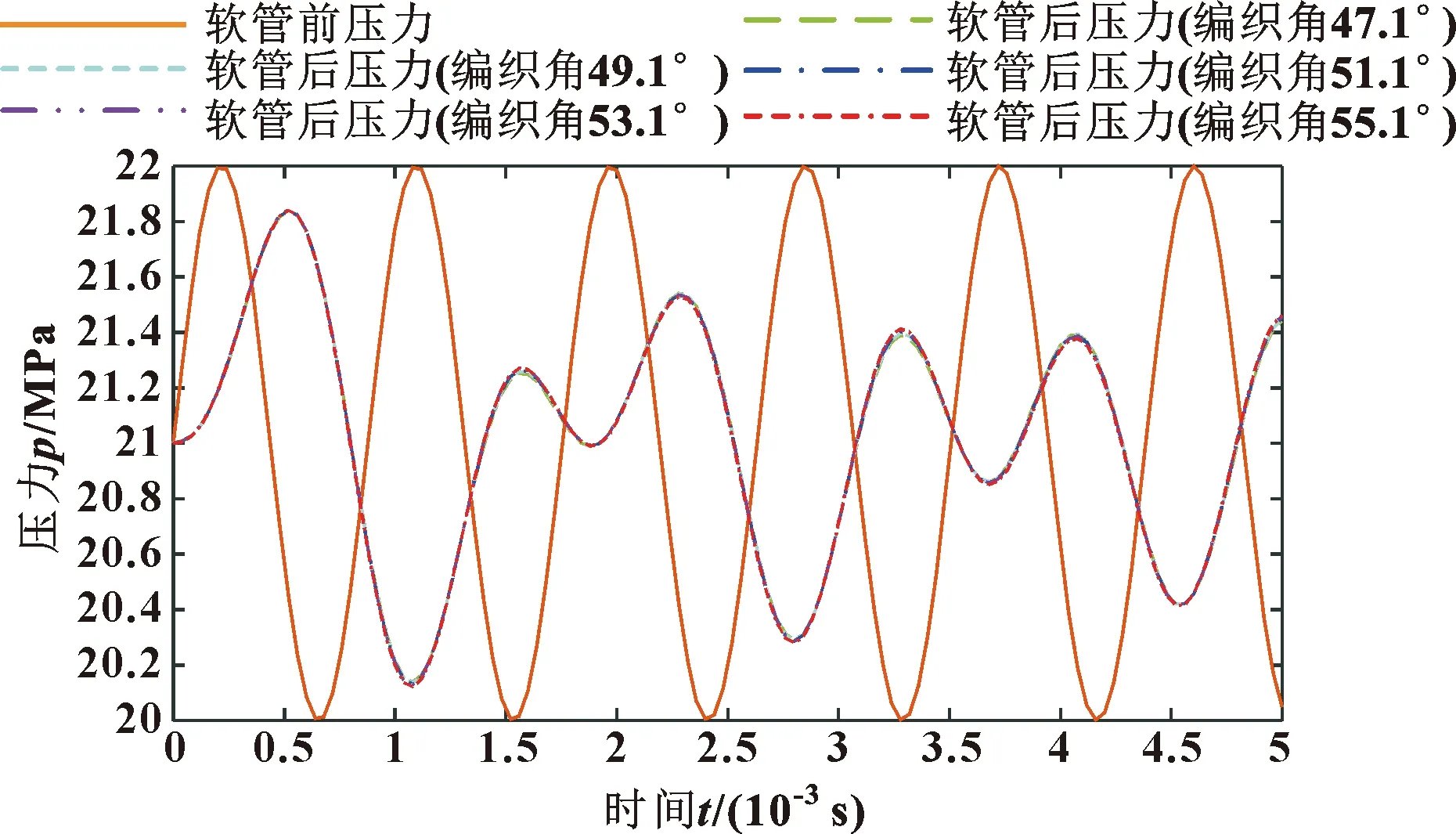
图10 不同编织角度压力脉动对比曲线

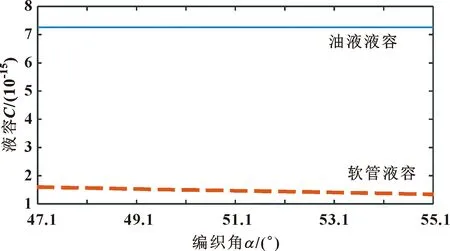
图11 不同编织角的软管与油液液容

2.3 钢丝直径对软管液容与压力传递的影响

其他条件不变的情况下，将钢丝直径分别设置为0.2、0.25、0.3、0.35、0.4 mm，当钢丝直径增大时，压力脉动抑制效果如图12所示，效果要好于前两种情况(油液液容随钢丝直径增大的变化情况如图13所示)，但是相比软管内油液压缩变形，软管变形对脉动抑制效果依旧很小。

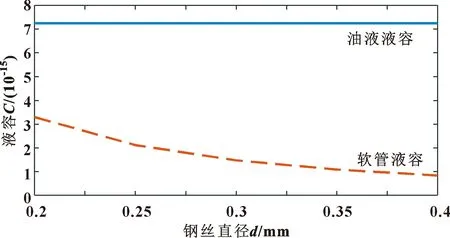
图13 不同钢丝直径的软管与油液液容

2.4 每股钢丝数量对软管液容与压力传递的影响

其他条件不变的情况下，每股钢丝数量分别设置为3、4、5、6、7，液容随之减小(见图14)，但是与软管内油液的液容相比，数量级过小对脉动抑制效果极为有限，且不如改变钢丝直径效果显著。因此如图15所示每股钢丝数对脉动抑制不起明显作用。

图14 不同每股钢丝数的软管与油液液容

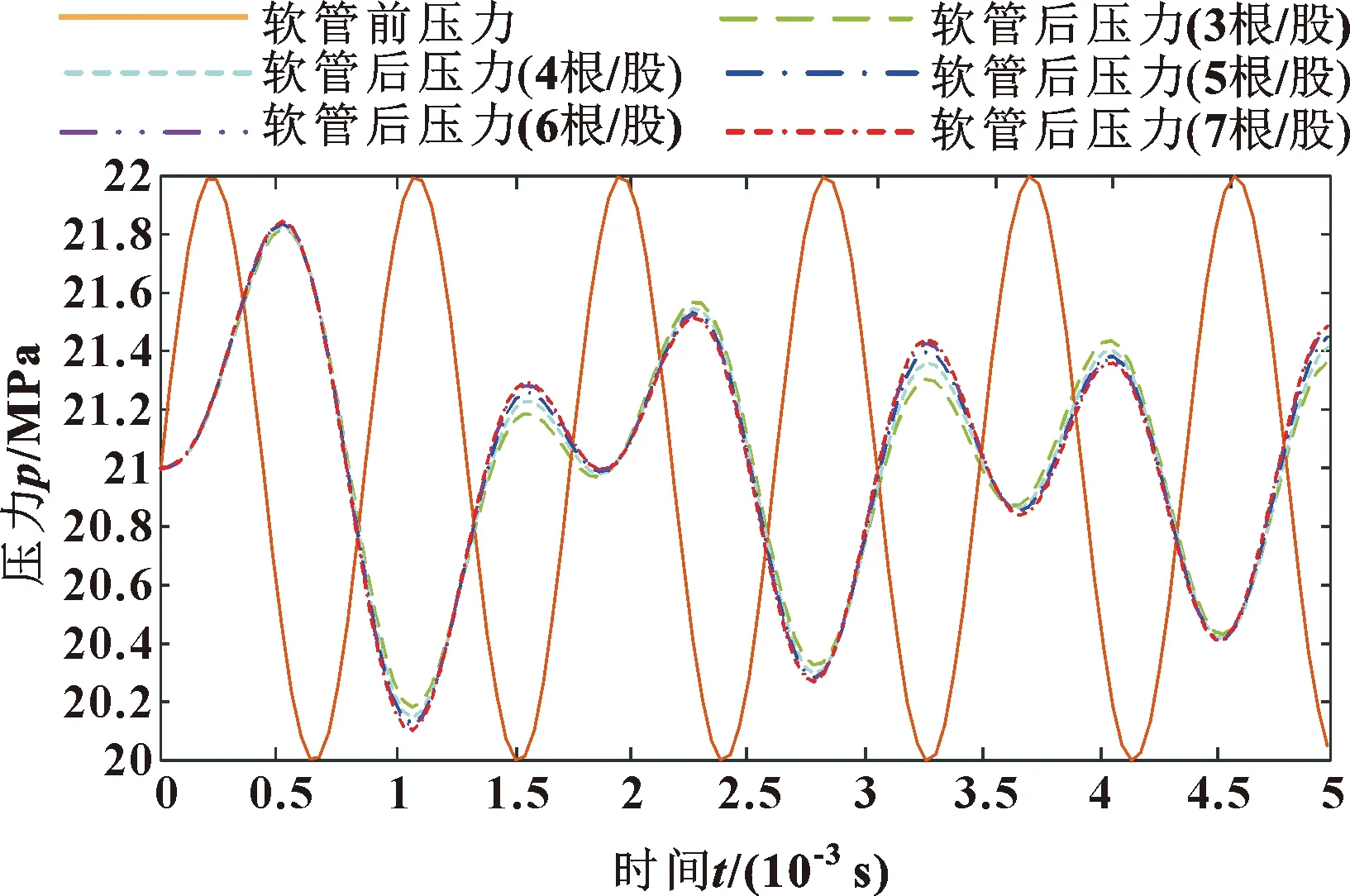
图15 不同每股钢丝数压力脉动对比曲线

2.5 软管通径对软管液容与压力传递的影响

其他条件不变的情况下，将软管内径分别设置为4.2、6.5、8.0 mm，压力脉动抑制效果如图16所示，可见软管长度不变情况下改变软管通径，抑制效果基本不变。

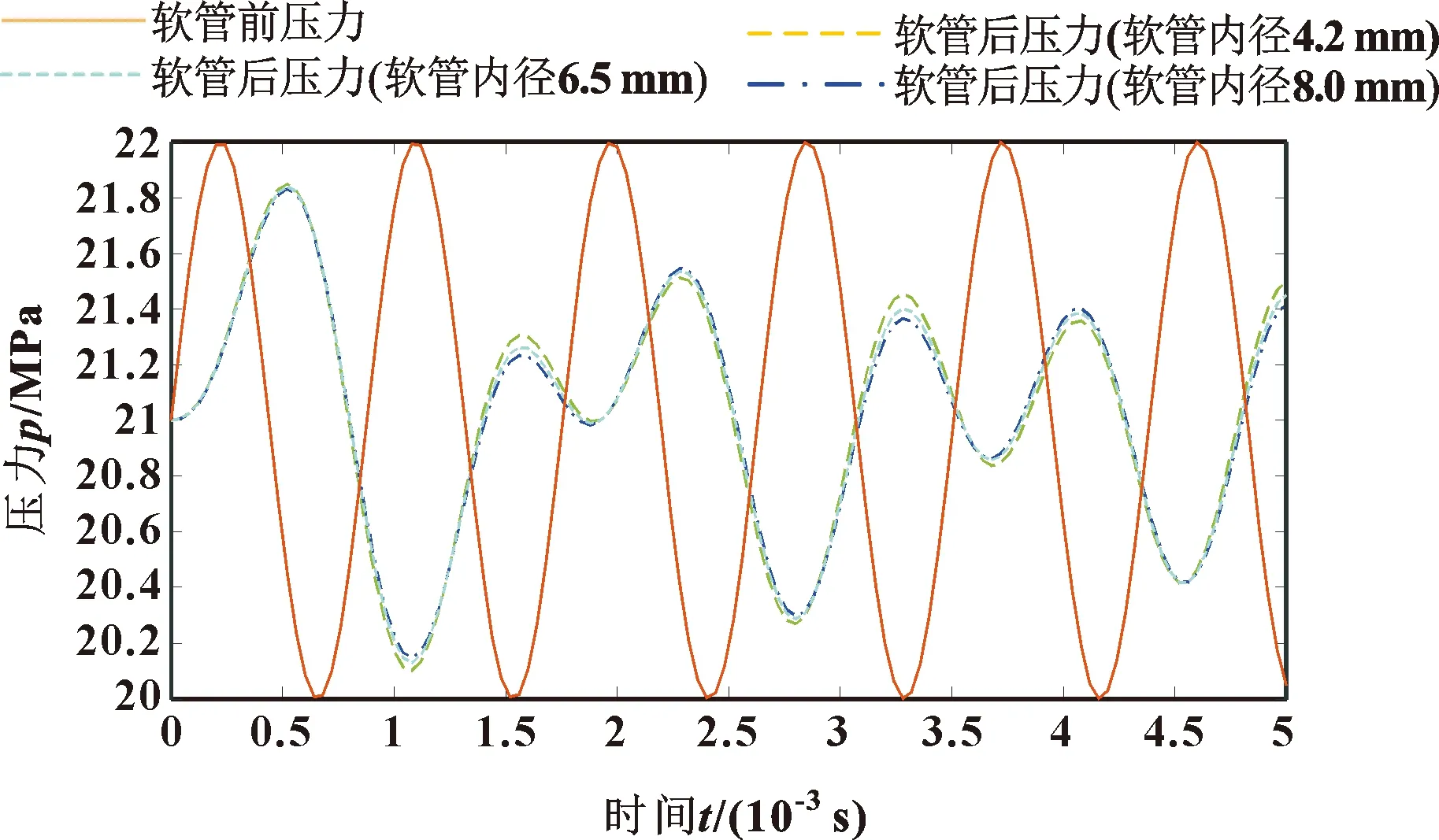
图16 不同软管内径压力脉动对比曲线

2.6 软管长度对软管液容与压力传递的影响

其他条件不变的情况下，将软管长度分别设置为300、350、400 mm。压力脉动抑制效果如图17所示，可见软管通径不变情况下增大软管长度，抑制效果显著提高。

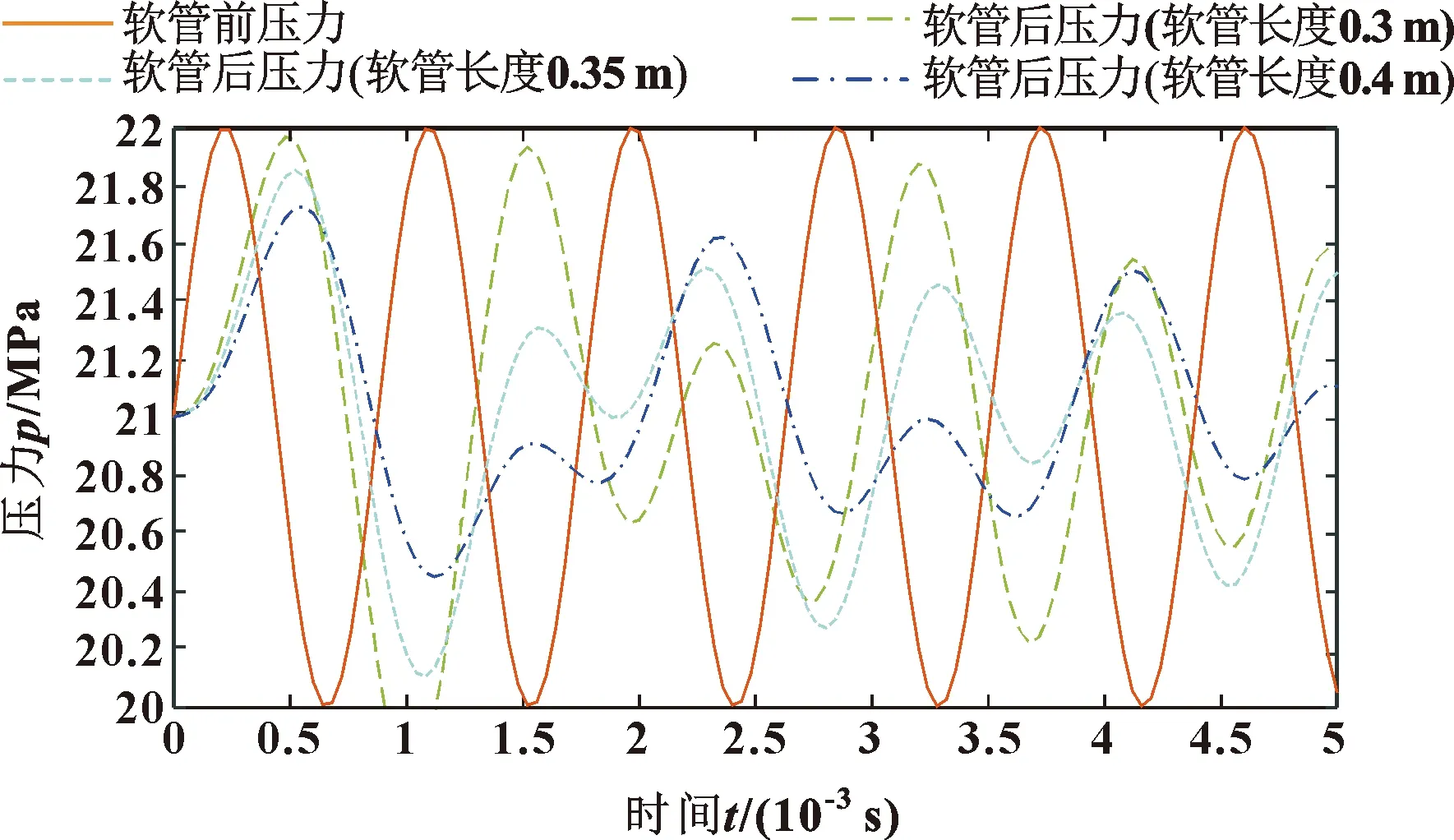
图17 不同长度压力脉动对比曲线

3 软管参数对固有频率影响的模态分析

3.1 软管编织股数对固有频率的影响

将编织层1单方向编织股数分别设置为8、9、10、11、12，编织层2单方向编织股数分别设置为10、11、12、13、14，软管编织层周向刚度如表1所示，并用体积分数计算等效密度与弹性模量输入ANSYS-Workbench，将简化软管三维模型导入Workbench中进行模态分析。得到结果如表1所示：随着编织股数增大各阶固有频率均有所增大，其中一、三阶固有频率离脉动激励频率1 140 Hz较远。当软管本身固有频率离脉动频率过近时会引起共振现象，严重损害软管和系统的寿命和健康运行。因此编织股数不宜太少，以使二阶固有频率远离激励频率。

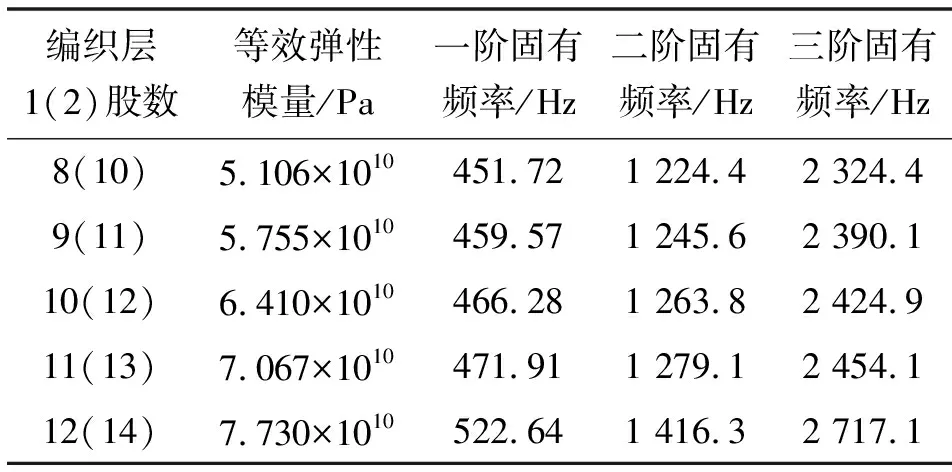
表1 不同编织股数情况下软管固有频率

3.2 编织角对固有频率的影响

其他条件不变的情况下，将编织角分别设置为47.1°、49.1°、51.1°、53.1°、55.1°，得到结果如表2所示，随着编织角增大各阶固有频率均有所增大，其中一、三阶固有频率离脉动激励频率1 140 Hz较远。编织角不能太小，应该大于等于47.1°。当编织角过小时，软管本身固有频率离脉动频率过近，会引起共振现象。

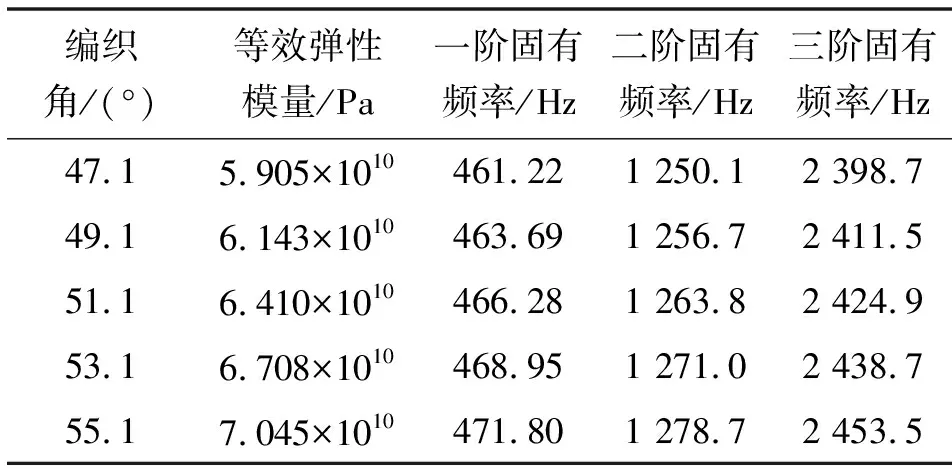
表2 不同编织角情况下软管固有频率

3.3 每股钢丝数对固有频率的影响

每股钢丝数量分别设置为3、4、5、6、7，得到结果如表3所示。随着每股钢丝数增大各阶固有频率均有所增大，其中一阶和三阶固有频率离脉动激励频率1 140 Hz较远。值得注意的是每股钢丝数量等于3时，软管的固有频率十分接近压力脉动的频率。

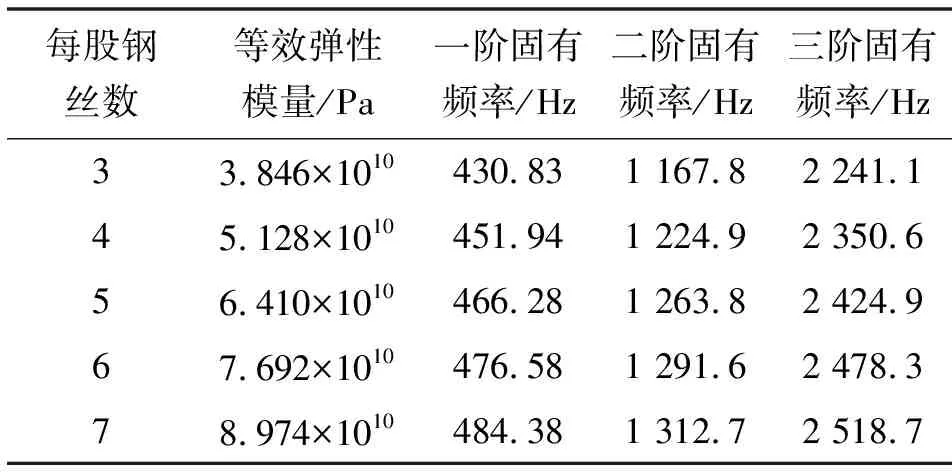
表3 不同每股钢丝数情况下软管固有频率

3.4 钢丝直径对固有频率的影响

将钢丝直径分别设置为0.2、0.25、0.3、0.35、0.4 mm，得到结果如表4所示。随着钢丝直径增大各阶固有频率均有所增大，当钢丝直径在0.25 mm与0.2 mm之间时，固有频率接近脉动频率。

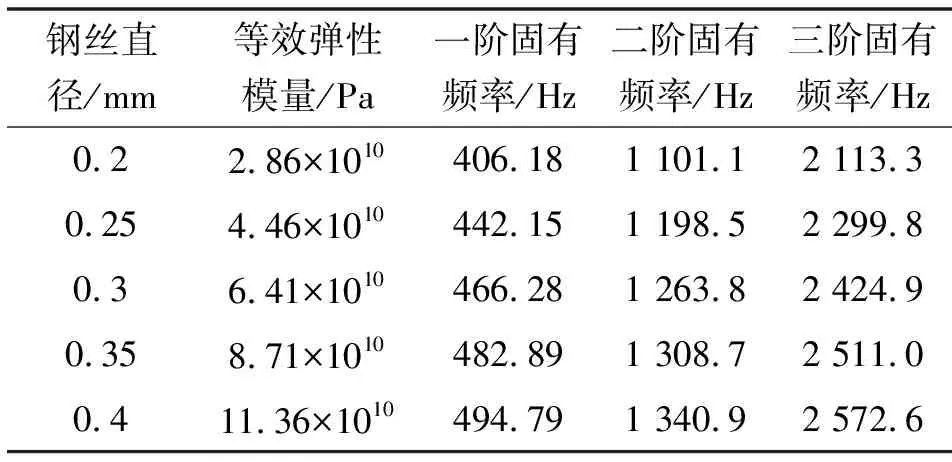
表4 不同钢丝直径下软管固有频率

3.5 软管内径对固有频率的影响

将软管内径分别设置为4.2、6.5、8.0 mm，得到结果如表5所示。随着软管内径增大，各阶固有频率均有所增大，3种内径情况下各阶固有频率均离脉动频率较远。

表5不同软管内径情况下软管固有频率

3.6 软管长度对固有频率的影响

其他条件不变的情况下，将软管长度分别设置为320、340、360、380、400 mm，得到结果如表6所示。随着软管长度增加，各阶固有频率减小，除380 mm外，其他长度软管固有频率距离脉动频率较远。

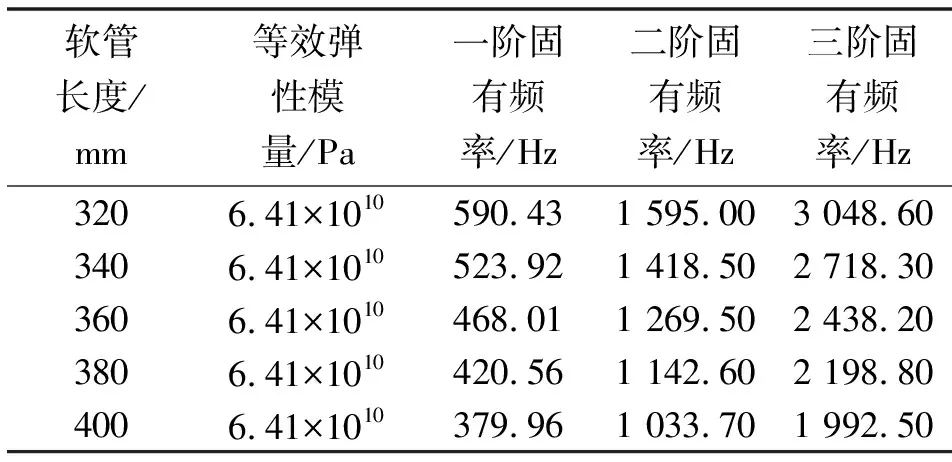
表6 不同软管长度情况下软管固有频率

4 应急放能源压力脉动实验

某型飞机起落架应急放能源最大压力和工作压力为21 MPa，此时负载缸保持完全伸出状态，柱塞泵的流量仅供自身泄漏，系统中的流量为0。在该工况下，柱塞泵产生的压力脉动通过泵口不锈钢编织软管、压油过滤器到负载缸。此时软管通径为6 mm，实际内径为6.5 mm，管长0.35 m，编织层1的编织股数为10，编织层2的编织股数为12，每股钢丝数为5，钢丝直径为0.3 mm，编织角为51.1°。测试软管前、软管后的压力脉动。测得压力脉动曲线如图18所示。

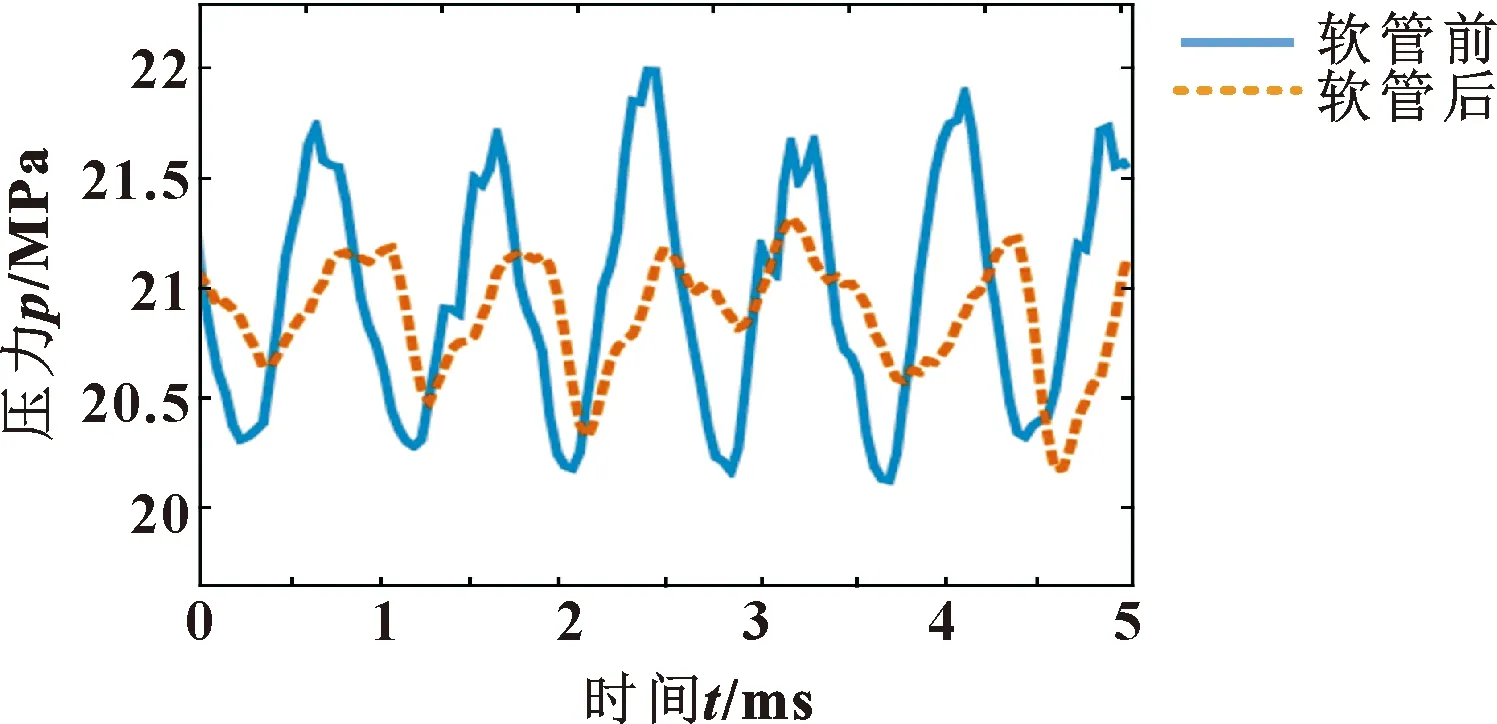
图18 带载21 MPa下软管前、后压力脉动实验曲线

可以看出：脉动幅值经过软管有衰减，软管的脉动衰减率为48%。再对两点的压力脉动曲线进行傅里叶变换，得到软管前、后压力脉动信号的频谱如图19所示。

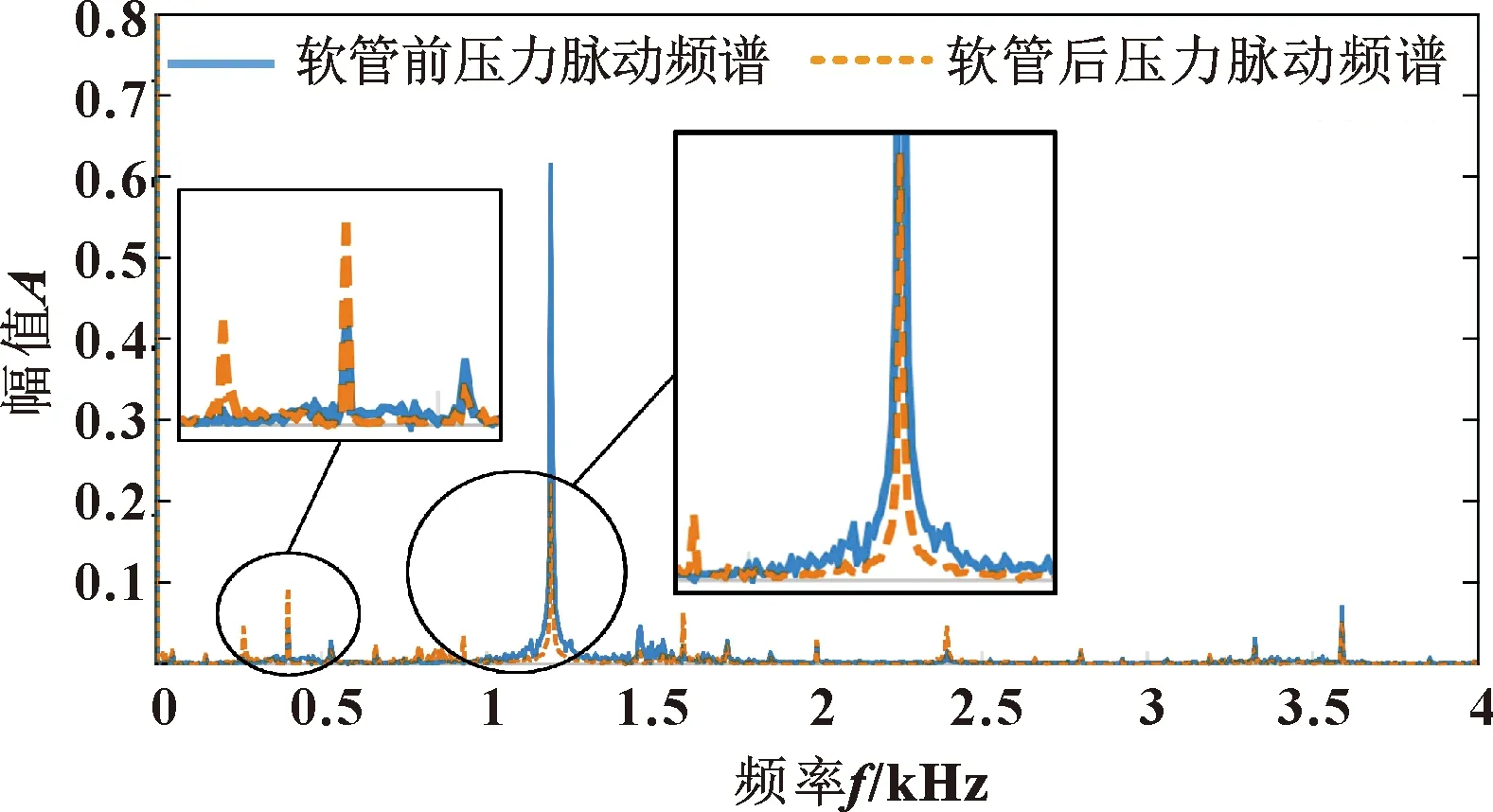
图19 带载21 MPa下软管前、后压力频谱

可以看出：软管前压力频谱曲线主频率是1 140 Hz，经过软管后各频率脉动幅值均减弱。对比图18和图20，可以看出脉动衰减效果与相同条件下仿真结果一致。

5 结论

采用参数化建模方法，从双层不锈钢编织本构模型入手，该模型可用于各种软管编织形式，通过实验一定程度上验证了该模型的准确性，并通过Simulink参数仿真模型研究了钢丝直径、编织股数、每股钢丝数、编织角等编织参数以及软管内径和软管长度等几何参数对不锈钢编织增强软管压力传递的影响。该模型的显著优势是利用精准的编织本构模型来计算软管各层刚度，得到电学比拟模型液容精确解析解，进而准确预测压力传递效果。但同时也存在着实验验证较为有限的问题，这也将是下一步研究的重点。