数控机床多轴联动铣削加工轨迹快速跟踪研究

赵鲁燕，李鹏，黄再辉

(桂林电子科技大学海洋工程学院，广西北海 536000)

0 前言

伴随科技水平持续提升，对机械加工产品的质量与精度的要求越来越高，产品各种零配件的加工环节朝着智能化方向发展[1]。为满足上述需求，提升机械加工产品及零部件质量与精度，需实时监控加工过程的各个环节，而对于机械加工刀具的加工轨迹监控尤为重要[2-4]。兼具高加工精度与自动化性能以及柔性等多种特点的数控机床，逐步应用至各类零部件加工等制造领域，同时在应用中其性能逐步改善[5]。随着制造领域竞争日益增强，为满足不同用户个性化需求，各制造企业对于加工零部件加工效率、质量以及精细化的需求越来越高，对数控机床的加工过程监控也越来越严格[6]。多轴联动数控机床是当前机械加工中的关键机械设备之一，能够有效提升企业加工的效率，提高企业产能。当前刀轴联动铣削加工已经成为现下自由曲面零件加工的一种关键加工方式，在模具加工、汽车与航天零件加工等领域内被大量运用[7-8]。数控机床多轴联动铣削加工过程中采用了加工工件相对铣削刀具轴线的平移进给运动与铣削刀具相对其轴线的旋转运动的一种复合运动形式，在刀具运动过程中会产生振动，使得正常切削过程受到干扰和破坏，导致多轴联动铣削加工轨迹偏离预设轨迹。为了有效降低其对零件加工质量的影响，需要快速跟踪多轴联动铣削加工轨迹，以及时减小加工轨迹误差[9]，提升加工精度，所以研究数控机床多轴联动铣削加工轨迹快速跟踪方法具有重要的研究意义。

卡尔曼滤波属于采用线性系统状态方程组，运用相关数据实现最佳预估的一种算法，同时可对数据内存在的噪声干扰等实施滤除处理[10-11]，其优点是鲁棒性强、效率高、误差低等，已经广泛应用在机械控制、导航、轨迹跟踪以及通信等领域中[12]。为了提升数控机床多轴联动铣削加工轨迹快速跟踪精度，本文作者将渐消因子融入到其中，并选取合适的卡尔曼系数，得到自适应卡尔曼滤波算法，通过强跟踪滤波运算提升跟踪精度。

综上所述，本文作者研究了一种数控机床多轴联动铣削加工轨迹快速跟踪方法，以期实现数控机床多轴联动铣削加工过程中加工运动轨迹的高效精准跟踪，为铣削加工过程监控、保障加工工件的精度与质量提供有效支撑。

1 数控机床多轴联动铣削加工轨迹快速跟踪方法设计

1.1 铣削刀具与工件坐标系构建

对于数控机床多轴联动铣削加工轨迹快速跟踪这一问题而言，多轴联动铣削刀具与加工工件坐标系间的转换关系是其基础与前提[13-14]。需通过构建多轴联动铣削刀具坐标系、加工工件坐标系以及参考坐标系，实现数控机床多轴联动铣削刀具加工轨迹的跟踪。本文作者以典型的六轴联动数控机床作为研究对象，六轴联动数控机床结构如图1所示。

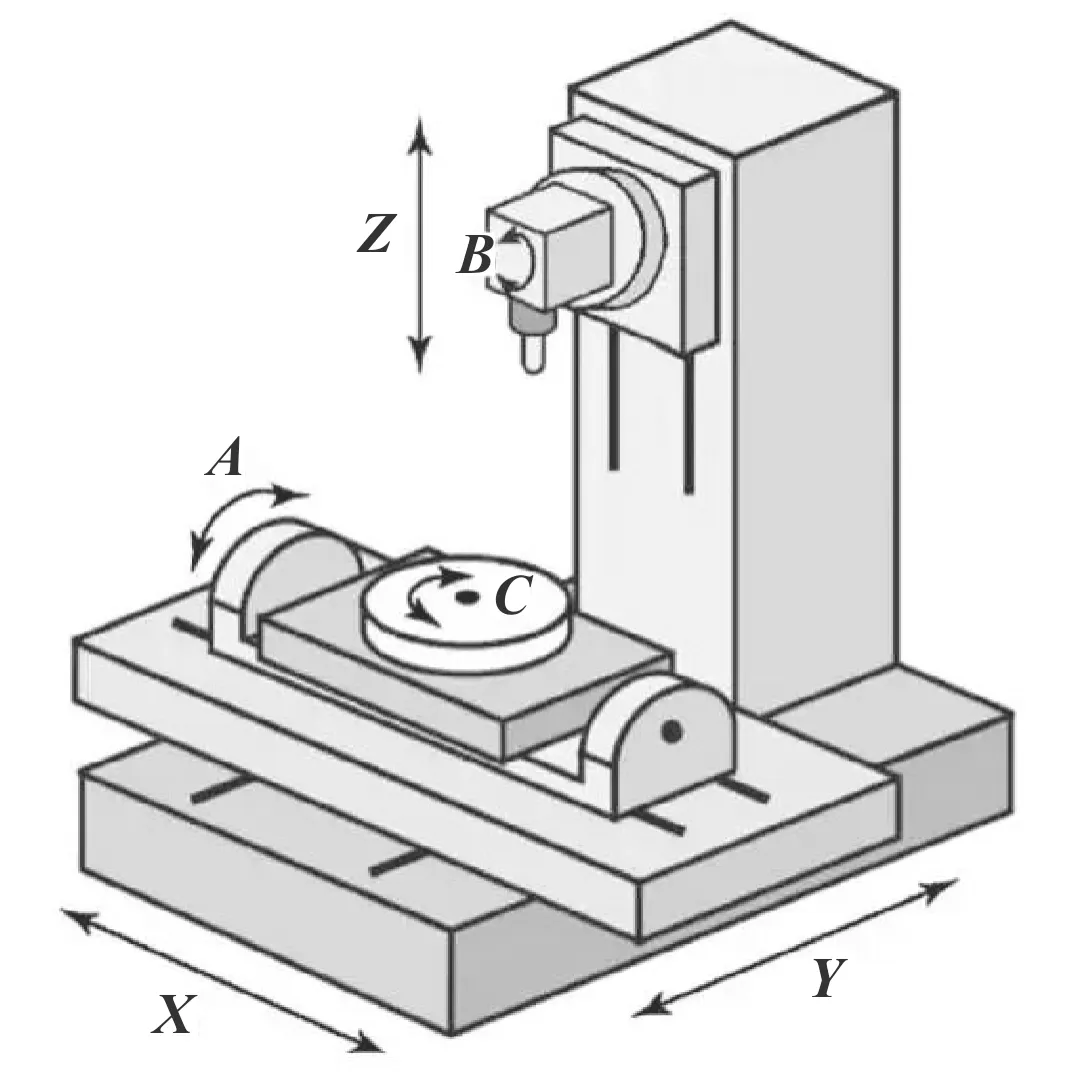
图1 六轴联动数控机床结构

分析图1可知，六轴联动数控机床具有3个平动联动轴X、Y和Z轴和3个旋转联动轴A、B和C轴，刀具为抛光轮。

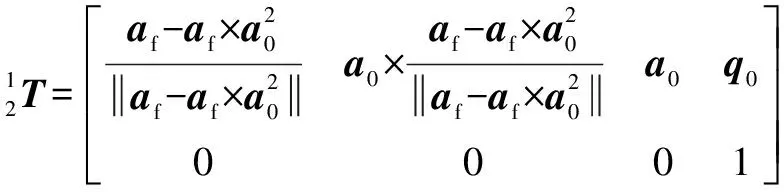
(1)

(2)

(3)

将公式(1)与公式(3)融合后，能够获得铣削刀具坐标系与加工工件坐标系的转换关系矩阵

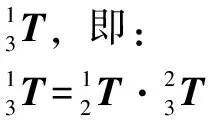
(4)

综合以上过程，完成数控机床多轴联动铣削刀具与加工工件的坐标系构建以及二者之间的转换。在此基础上，建立数控机床多轴联动铣削加工运动学模型，以期为数控机床多轴联动铣削加工轨迹的快速跟踪奠定基础。

1.2 数控机床多轴联动铣削加工运动学模型建立

建立数控机床多轴联动铣削加工运动学模型的目的是映射铣削刀具相对加工工件的运动为多个联动轴(文中以6个联动轴为例)的运动，也就是在加工工件位置不变的情况下，转变铣削刀具的加工运动轨迹为多个联动轴的运动轨迹，为之后实现铣削加工轨迹的快速跟踪奠定基础。在加工工件位置不变的情况下，可通过铣削刀具的轴线矢量s与中心点e描述铣削刀具的运动轨迹，二者之间的关系可表示成：

(5)

式中：在铣削刀具坐标系内3个坐标轴方向上轴线矢量s与中心点e的分量分别用sx3、sy3、sz3与ex3、ey3、ez3表示。

2008年6月，国务院发布了第二批国家级非物质文化遗产名录，评书名列其中。某种意义上，这也是评书生存困境的折射。

本文作者针对6个联动轴的数控机床展开研究，主要由3个旋转联动轴A1、A2、A3与3个平移联动轴X、Y、Z构成。位于旋转盘上的联动轴A2和A3处在加工工件位置，其中，A2轴的角度为-90°，A3轴的轴线平行于A1轴，便于加工上下料。创建数控机床整体坐标系，以便于对其多个联动轴的运动实施描述。多轴联动数控机床整体坐标系见图2。

图2中，数控机床整体坐标系用Ow-xwywzw表示；抛光轮摆动与平移坐标系分别用O3d-x3dy3dz3d与O3b-x3by3bz3b表示；加工工件的回转坐标系用O′1-x′1y′1z′1表示，刀具抛光轮中心点e与O3b重叠。假设O′1-x′1y′1z′1与Ow-xwywzw重叠，那么矢量γ1等于0。每个联动轴不运动时的状态即为数控机床的原始状态，在此状态下，抛光轮平移坐标系下其摆动坐标系原点的坐标即为矢量γ2，它的齐次坐标表现形式如下：

γ2=(γ2x3,γ2y3,γ2z3,1)

(6)

式中：X、Y、Z轴3个方向上的分量分别用γ2x3、γ2y3、γ2z3表示。综合以上过程，可创建出铣削刀具抛光轮轴线矢量s、中心点e同多个联动轴运动间的数学模型，即数控机床多轴联动运动学模型：

(7)

式中：旋转与平移两种运动的齐次坐标变换矩阵分别用R与T表示；旋转联动轴A1、A2、A3的转动角依次用βA1、βA2、βA3表示；u=(ux3,uy3,uz3,1)，ux3、uy3、uz3分别表示平动联动轴X、Y、Z的运动量。将公式(7)展开能够得到以下公式：

(8)

因s属于单位矢量，公式(8)中拥有旋转联动轴A1、A2、A3的旋转角度运动量，故可将该公式看作冗余方程组。因A3轴连接在加工工件上，能够直接操控加工工件的转动，故该轴可作为已知运动量的冗余联动轴。此种情况下，另外5个联动轴的运动量可通过公式(9)—(11)表示成：

βA1=-arcsin(sx3sinβA3+sy3cosβA3)

(9)

(10)

(11)

1.3 数控机床多轴联动铣削加工轨迹快速跟踪

通过构建加工工件和铣削刀具瞬时坐标系，建立数控机床六轴联动的铣削加工运动学模型，结合该模型与强跟踪卡尔曼滤波轨迹跟踪方法[15]对数控机床多轴联动铣削加工轨迹实施快速跟踪，获得铣削刀具的加工轨迹，依据加工轨迹跟踪结果分析目标铣削刀具实时加工的运动状态。

通过公式(7)对数控机床多轴联动铣削刀具的当前运动状态实施推理，但因推理过程中存在噪声的干扰，会导致推理结果产生不确定性。对于此种不确定性，在此选用协方差矩阵呈现。假设运动状态协方差主要用Q表示，在其中加入运动状态的齐次坐标转换矩阵R与T之后，能够得出：

(12)

式中：t时刻与其前一时刻的运动状态协方差分别用Qt与Qt-1表示；t时刻与其前一时刻的运动状态分别用Xt与Xt-1表示。t时刻的实际观测矩阵Bt为

Bt=GXt+kt

(13)

式中：t时刻的观测噪声用kt表示，它的协方差矩阵用C表示；观测参数矩阵用G表示，且G=[1 0]。t时刻铣削刀具运动状态的更新公式为

(14)

Kt=Qt-1GT(GQt-1+C)-1

(15)

设在t时刻状态下的最佳预估值为Xt，为实现持续迭代运算，需对运动状态协方差值实施更新，更新公式为

(16)

2 实验结果分析

以某六轴联动数控机床为例，运用文中方法对其铣削抛光加工轨迹实施快速跟踪，通过分析文中方法的实际跟踪结果，检验此方法的实际应用性能。此次实验所用的六轴联动数控机床如图3所示。

图3 实验用六轴联动数控机床

在实验数控机床多轴联动铣削抛光加工过程中，加工工件与数控机床的X轴和Z轴均为平行状态，铣削抛光加工所用的抛光轮厚度与直径分别为26 mm与120 mm，其平均转速与中心点的运动速率均值分别设定为1 010 r/min与3 010 mm/min。由实验机床铣削刀具的切削刀刃上随机选取A～D4个点作为文中方法的跟踪对象，主要通过下述过程确定这4个点的坐标：

将刀具试切后所在位置作为铣削刀具坐标系中的预设坐标值，通过机床操作面板手动输入到数控车床相应的刀具补偿单元中，数控系统对预设值进行坐标转换，以此进行铣削刀具坐标系原点定位，从而将机床坐标系原点O机床偏移到所需的铣削刀具坐标系原点，搭建以O为原点的铣削刀具坐标系，以此确定这4个点的实际坐标。

各点在铣削刀具坐标系中的坐标情况如表1所示。

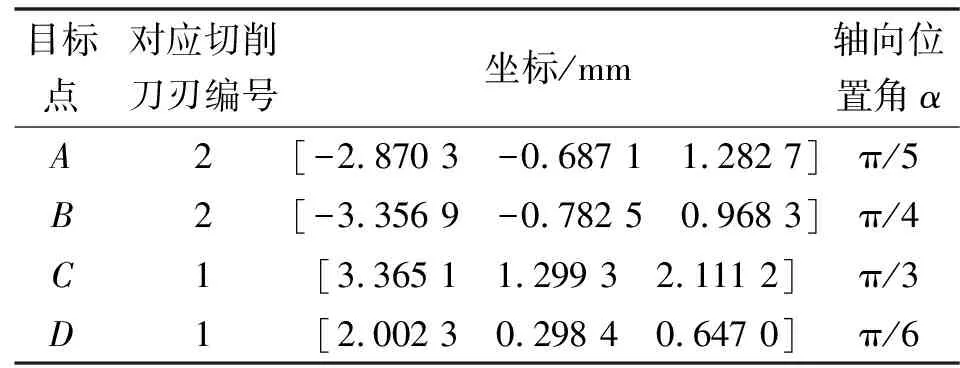
表1 各点在铣削刀具坐标系中的坐标

实验机床铣削刀具的关键参数如表2所示。

表2 实验机床铣削刀具关键参数

通过文中方法对实验机床铣削加工过程实施跟踪，所获得的某段时间内铣削加工过程中4个目标点的轨迹情况如图4所示。

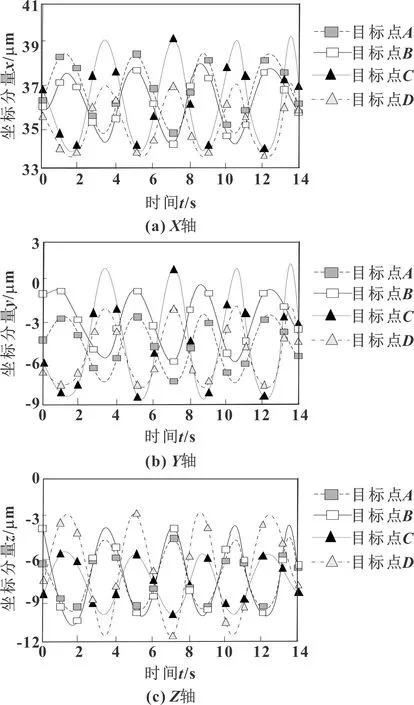
图4 铣削加工中4个目标点各方向的跟踪轨迹

由图4可知：文中方法能够跟踪实验机床铣削加工过程中铣削刀刃上各目标点在不同方向上的运动轨迹，有效呈现出实验机床的铣削加工运动过程及运动状态。

对文中方法所获取的各个目标点运动轨迹实施检验，分析此方法的轨迹跟踪效果。以各目标点实际位置变化情况为对比对象，统计文中方法所得的目标点运动轨迹的误差情况，以检验此方法的轨迹跟踪精度。所得统计结果如图5所示。

图5 文中方法所得各个目标点轨迹误差

分析图5可知：文中方法跟踪所得目标点A三个方向轨迹误差最高值分别为0.056 2、0.043 8、-0.028 1 μm，目标点B三个方向轨迹误差最高值分别为0.062 5、0.046 9、-0.031 3 μm，目标点C三个方向轨迹误差最高值分别为-0.068 8、-0.046 9、0.031 3 μm，目标点D三个方向轨迹误差最高值分别为0.034 4、0.065 6、-0.025 1 μm，4个目标点各个方向跟踪轨迹误差均低于0.1 μm。对比可知，文中方法的轨迹跟踪误差低，所获得各目标点运动轨迹精准可靠，实际跟踪效果理想，可用于数控机床多轴联动铣削加工轨迹的实际跟踪中，为有效控制加工精度提供帮助。

基于此，对文中方法的跟踪速度实施检验，以各个目标点的运动轨迹跟踪用时为指标，从全部跟踪轨迹目标点中各随机抽取3个目标点，统计文中方法跟踪到各个目标点的用时情况，所得检验结果如表3所示。

经过计算可知：文中方法对于点A跟踪平均用时1.121 ms，对于点B跟踪平均用时1.069 ms，对于点C跟踪平均用时1.164 ms，对于点D跟踪平均用时1.150 ms，说明该方法跟踪平均用时低于1.2 ms，跟踪用时少，跟踪速度较快，能够满足数控机床的多轴联动铣削加工过程中对跟踪速度的需求。

3 结束语

数控机床的多轴联动铣削加工过程监控是企业加工各类零部件过程中有效把控加工质量的关键环节，高效精准地跟踪铣削刀具的运动轨迹尤为重要。本文作者针对一种数控机床多轴联动铣削加工轨迹快速跟踪方法展开研究，通过构建铣削刀具和加工工件坐标系及参考坐标系，实现了铣削刀具坐标系与加工工件坐标系之间的转换，建立数控机床多轴联动铣削加工运动学模型，结合强跟踪卡尔曼滤波轨迹跟踪方法完成对其加工过程中运动轨迹的快速跟踪。将此方法应用到实际六轴联动数控机床的铣削加工的应用结果表明：此方法能够实现对铣削加工中铣削刀刃上任意目标点的运动轨迹跟踪，所得跟踪轨迹误差低，与实际运动轨迹几乎能够吻合，且跟踪速度较快，能够满足实际加工中快速获得铣削加工轨迹需求，达到实时高精度铣削加工轨迹跟踪效果，为铣削加工质量提供保障。但本文作者并未针对跟踪过程中卡尔曼滤波噪声的效果实施检验，同时实验中所选取的实验目标点仅为铣削刀刃上的部分点。在后续研究中，应继续针对跟踪过程的卡尔曼滤波噪声实际效果实施检验，并由铣削刀刃上选取出更多的目标点实施加工过程中的运动轨迹跟踪，为文中方法的实际应用提供更完善的支撑。