利用衍生特征预测新冠疫情的随机森林方法

龙 铁,付宇笙,王文达,费 宁

(南京邮电大学 计算机学院,江苏 南京 210003)

0 引 言

随机森林[1-2]是一种机器学习算法,相较于决策树,能很好地防止过拟合;在面对高维复杂的数据时,能较好地容忍噪声值和离群值[3];同时由于它实现简单,学习速度快,在天气预报、疾病分析、图像识别等众多领域都得到了应用。当下新冠肺炎病毒具有高传染性和高隐蔽性的传播特性,产生的疫情数据繁多复杂。在分析原始新冠疫情数据的基础上,该文通过衍生出新的关键特征值,对原本不均衡的数据集分组使用随机森林进行新冠疫情发展趋势的预测,从而有效提高整体的预测准确率。

1 相关研究

当前已经有许多方法用于新冠疫情的预测。常用的预测方法概括为两大类:(1)基于传统模型的预测;(2)基于机器学习的预测。

基于传统模型的预测方法主要包括:仓室模型[4](SIR和SEIR等)、时滞动力学模型[5](TDD-NCP等)。在通常的传染模型中,通过人群间相互转移的传播学机制建立常微分方程组来描述疫情的发展,建立仓室模型。时滞动力学模型在构建时考虑潜伏期对于传播时间的滞后效应,实际数据的拟合值与预测值在传播初期较容易吻合。此类模型对于特定地区有着很好的拟合效果,但不同国家疫情环境不同,比如人口密度、隔离措施、医疗条件等,换一个地区往往既有模型难以适应,需要重新调整,工作较为复杂。

基于机器学习的预测方法主要包括[6]:线性回归(Linear Regression,LR)、回归模型(Least Absolute Shrinkage and Selection Operator,LASSO)、支持向量机(Support Vector Machine,SVM)、指数平滑法(Exponential Smoothing,ES)以及随机森林(Random Forest,RF)等。其中随机森林能够比较好地适应高维度数据,具备较好的抗噪音能力以及免特征选择等优点,更适合预测新冠疫情发展趋势。在实验过程中发现,随机森林虽然能够对所选新冠疫情数据集合做出较好的拟合和预测,但由于疫情数据各地区差异较大,回归树进行判决时无法选择最优阈值,从而牺牲了判决的准确率。

在对现有传统模型和机器学习方法研究比较后发现,大多数研究更重视算法本身的应用和性能比较,却忽视了对现有数据的预处理。不同数据样本个数和特征差异巨大,其中不乏重复甚至错误的特征存在。对于这样的数据,进行适当的预处理比如降维或者增加衍生特征会明显提高预测的准确性。这正是本研究的切入点和主要贡献所在。该文使用一种在原有样本的特征值上进行变换和组合的方法,增加了新的特征值。对于差异较大的特性,通过筛选出异常数据并单独进行训练,从而更好地处理了异常数据干扰的问题,得到了较好的泛化性能。

2 设计思路

2.1 CART回归树和性能指标

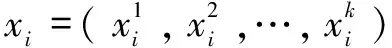
(1)

使用均方误差(Mean Square Error,MSE)最小化得到的最佳参数:

(2)

给每个叶子节点赋予相应的预测值:

(3)

其中,

(4)

式(4)中的∏为布尔类型,若样本落入区域则取值为1,若样本没有落入区域则取值为0。

遍历样本中所有的特征值和不同分割点,使得式(3)中平方误差最小时,则回归树训练完成。

回归树的评价指标包括平均绝对误差MAE1(Mean Absolute Error)和最大绝对误差MAE2(Max Absolute Error)[8]:

(5)

(6)

2.2 随机森林集成学习模型

随机森林是采用2.1节所示的CART回归树作为基本分类器的一个集成学习模型,包含多个由Bagging集成训练得到的决策树。预测过程如图1所示。

输入样本数据后,根据阈值访问下一个子节点,到叶子节点处结束,将所有叶子节点返回的决策树预测值求平均得到该样本的预测值。

CART回归树训练子集的方式是有放回的抽样,并且每个子集的样本数量必须和原始样本数量一致,但是子集中允许存在重复数据。CART树还对原始数据集上的特征属性进行随机采样,但采样的属性集是原始特征集的子集。

2.3 数据预处理和特征值选取

该文采用源于GitHub上的Johns Hopkins大学系统科学与工程中心提供的美国疫情相关数据[9-10],并从中人为选取了部分特征,去掉了一些冗余信息。表1列出了该数据集的数据类型和特征。

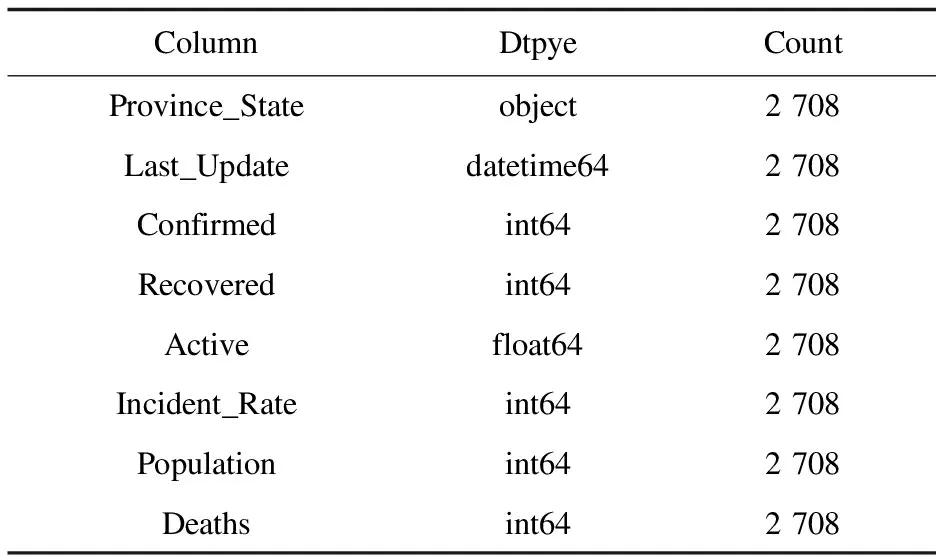
表1 Johns Hopkins新冠数据集特性

其中,Province_State是美国的州名,Last_Update是前一天数据更新的时间,Confirmed是累计确诊人数,Recovered是累计治愈人数,Active是现阶段的确诊人数,Incident_Rate是传染率,Population是州人口数,Deaths是累计死亡人数,Dtype表明数据类型。实验时间范围是2020年9月2日至2020年10月27日,共56天。样本共有2 708例。

原始数据中的Province_State和Last_Update对预测没有实际意义,Deaths也可以从Confirmed和Recovered中推算出来,不是一个独立变量。基于此,从清洗后的数据集中选取以下五个特征,如表2所示。

表2 随机森林实验特征值集

3 实验与分析

3.1 数据集的划分

数据集一般划分为训练集和测试集,训练集用于训练模型,测试集用于检验模型的效果。在模型建立的过程中,由于采用的数据跟时间有明显的相关性,因此以数据更新时间(Last_Update)作为组别,对数据按照留一组(leave-one-group-out)的方法来划分训练集和测试集[11],划分过程如图2所示。

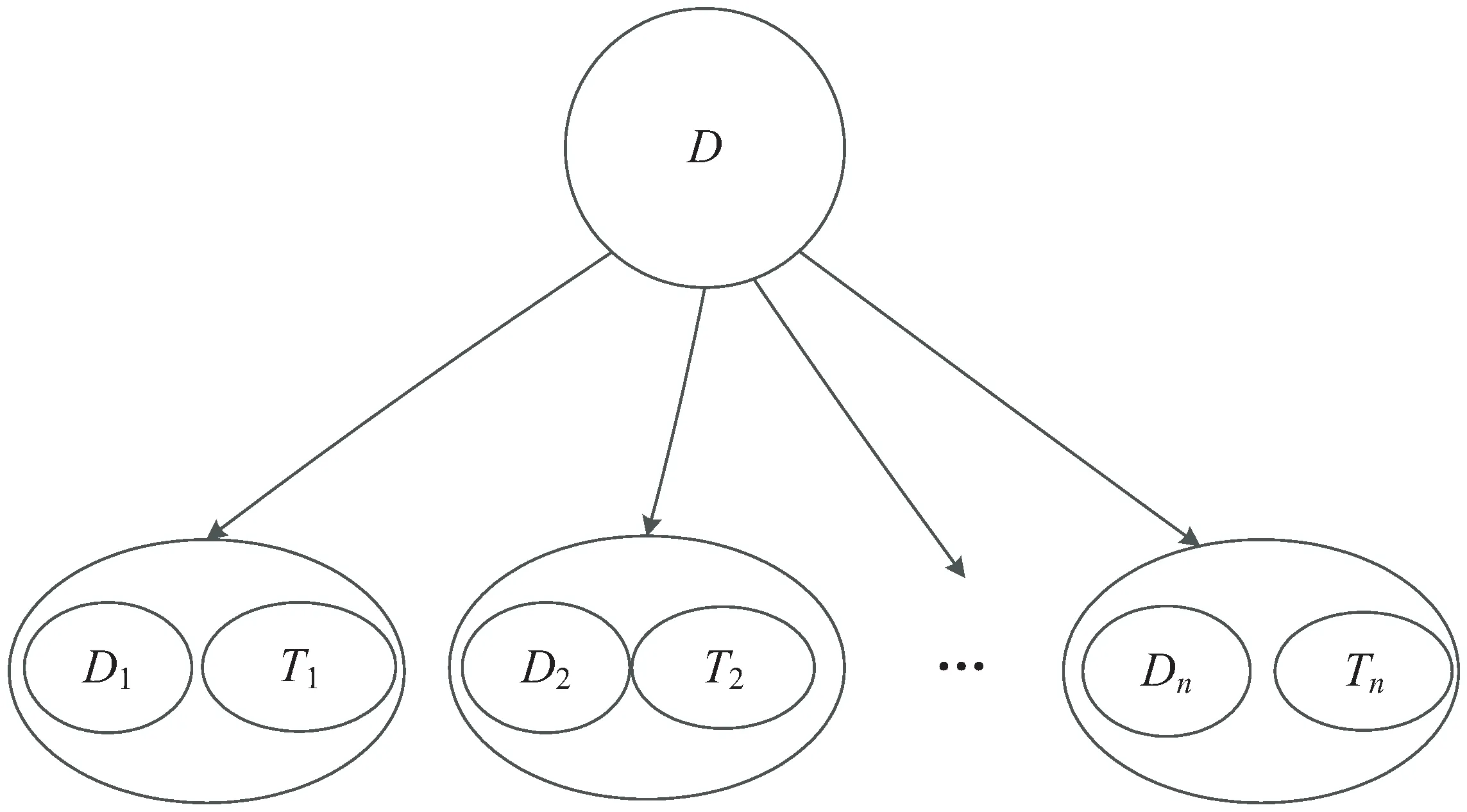
图2 数据划分

其中,D是原始数据集,D1是划分出来的第一个训练集,T1是划分出来的第一个测试集,D1中包含了除T1所在日期外的所有样本,T1中仅有一天的样本。如此反复,对原始的数据集进行多次划分,直到所有可能的训练集和测试集划分完毕。划分出来的训练集和测试集用于调整参数的交叉验证。

模型建立之后,需验证机器学习的效果,在此过程中,训练集则采用56天中的前49天进行训练,选取最后7天作为测试集进行验证。

3.2 模型的建立

表3列出了初始构建随机森林模型使用的参数。

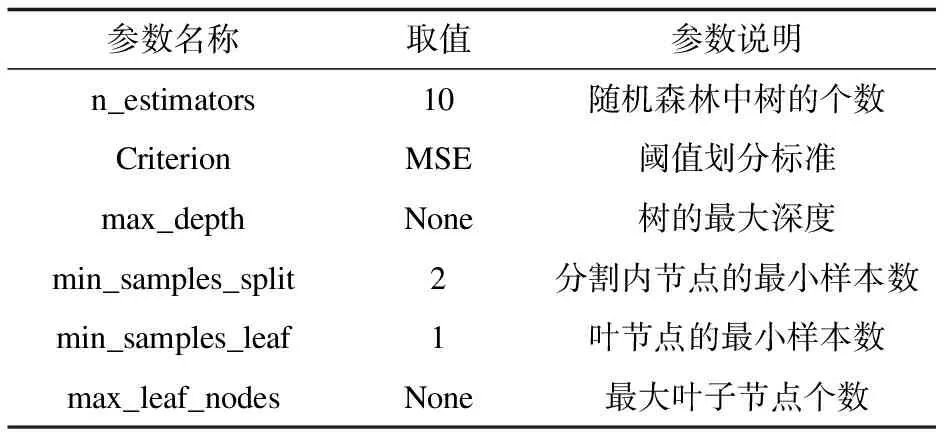
表3 随机森林部分参数

依据表3的随机森林参数,获得的拟合结果如图3所示。其中横坐标代表天数,纵坐标代表美国的总死亡人数,可以明显地观察到训练集前49天实际值和拟合值基本吻合,有着较高准确度。49天以后的实际值和预测值偏差较大,呈下降趋势。

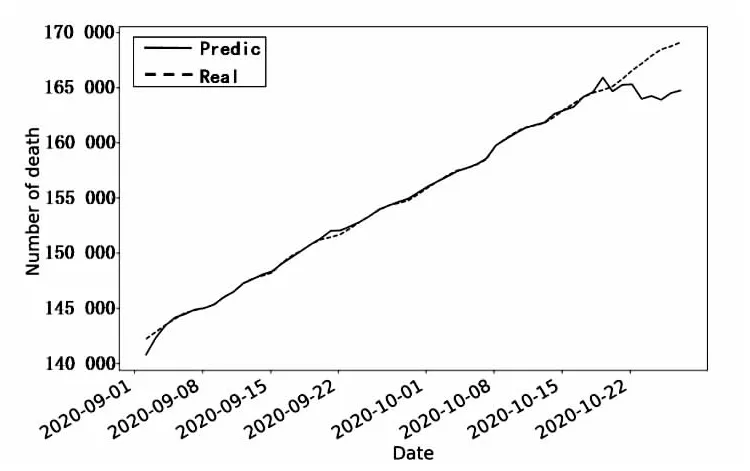
图3 模型未调参的结果

常用的超参数优化方法有Grid Search[12](网格搜寻)和Random Search[13](随机搜索)。由于随机搜寻的优化效果不稳定,该文采用Grid Search进行调参,对每一组的数据进行尝试,确保得到最佳超参数组合。

通过总结天津职业技术师范大学汉语国际教育专业极参与人文社科类学科竞赛的经验教训，成败利钝，可以看出，人文社科类学科竞赛对衡量文科专业的教学质量而言是非常重要的量化标准，对于提升学生思想道德水平和人文素养、实施社会主义核心价值观教育更具有潜移默化的涵养作用。积极组织、引导、培训文科学生参与到各层次的学科竞赛活动之中，有利于以教学相长的方式推动教学改革工作，提升教学质量，也能有效促进高校的思想政治教育的改革与发展。如何继续长效推进思想政治教育与人文社科类学科竞赛的紧密结合，完善工作和激励机制，发挥其更大的平台辐射作用，是目前我们继续思考和探索的重要课题。

从调参之后的结果图可以看出,调参的效果不明显,在49天之后的拟合效果偏差仍然较大。这表明随机森林模型对训练集匹配良好但与验证集差距明显且参数调优效果不佳。该预测结果表明,训练过程可能出现了过拟合或者现有的数据集并没有遵循特定趋势。

为了验证是否出现了过拟合的情况,将原训练集进一步划分为训练集和测试集,测试集为训练集的子集,并且子集中的样本为原训练集中随机抽取的样本。对新的训练集和测试集用随机森林进行学习和验证,学习曲线如图4所示。

图4 随机森林学习曲线

图中,横坐标代表学习的样本数,纵坐标代表验证时的准确率。在样本数达到1 200时,测试曲线基本拟合训练曲线,并且无论是测试集或者是训练集都与实际数据有着比较好的吻合效果,这表明模型学习效果良好,因此在该样本集合上的过拟合的可能性较低。

3.3 差异化处理

针对图3建模后49天拟合效果偏差较大这个问题,进一步从数据样本分析原因。数据分布如图5所示,从样本特征值分布图看出,少部分样本集中在高人口,高死亡和高确诊分布,部分样本呈现相近确诊,相近人口,但死亡人数差距大的复杂情况。由此该研究提出差异化处理。

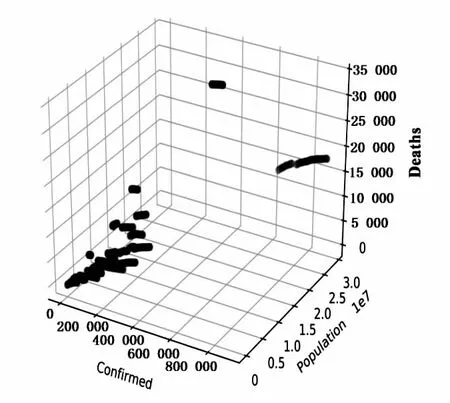
图5 样本特征值分布

根据随机森林得到的特征重要性[14-15]如表4所示。

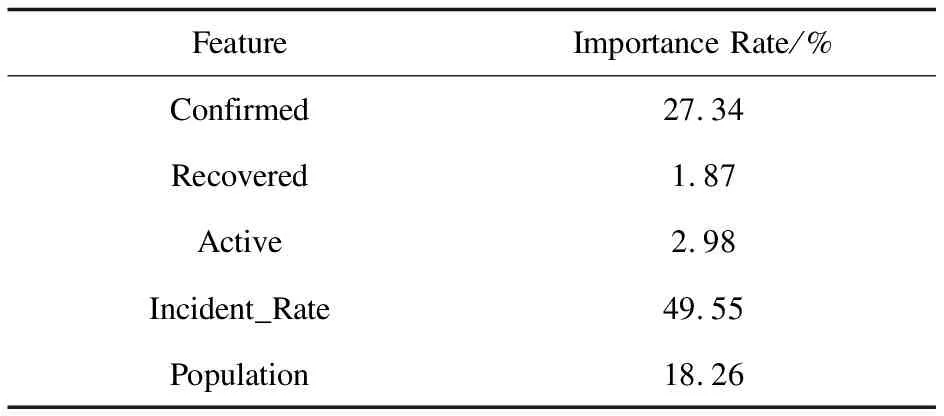
表4 特征重要性

可以发现,累计确诊患者数(Confirmed)和州人口数(Population)的重要性最为显著。表明回归树在划分子节点的过程中,较多使用这两个特征进行划分,因此随机森林对这两个特征的依赖性强。能够判断若两个州在累计确诊患者数(Confirmed)和州人口数(Population)两个特征相似的情况下,拥有差异显著的死亡人数d1和d2,回归树在训练过程中,会将这两个州划分到一个叶节点中,从而输出平均预测值r,r在d1和d2的影响下,只能折中为d1和d2的平均值。因此,r无论是对于d1或者是d2而言都具有很高的偏差,从而造成测试集中出现高偏差的情况。

出现以上情况的原因可以归为美国各州的医疗能力不同,地区环境不同,每一天的防控情况不同,因此,部分确诊人数和州人口数近似的地区之间在死亡人数上有巨大差异。此时,需要一个衡量医疗能力的指标,来体现出差异性,并作为特征值供随机森林模型学习训练,从而降低误差,最后达到泛化处理误差的效果。

该文将死亡率作为衡量每个样本医疗能力的指标,死亡率(Death Rate)定义如式(7)所示:

(7)

其中,Rd代表死亡率,D代表死亡人数,C代表确诊人数。根据每一个样本的死亡率划分医疗能力等级,不同死亡率的样本对应医疗能力等级范围为1到n。为了确定最佳划分的等级个数n以及使最佳等级划分阈值t1,t2,…,tn误差最小,采用迭代划分的方法遍历每种组合,寻找最优解。等级个数n取值范围为1到k,k为样本总个数。当n=k时,表明每个样本的医疗能力等级都不同,可以直接使用每个样本的死亡率作为衡量防控能力的指标进行划分。

图6是部分不同的n值(2～49)对应平均绝对误差MAE1以及最大绝对误差MAE2的取值。在图6中,为了使MAE1的变化更加直观,将MAE1放大了10倍。可以发现,在等级个数为39时,得到的MAE1和MAE2最小,因此确定最优划分等级个数为39。

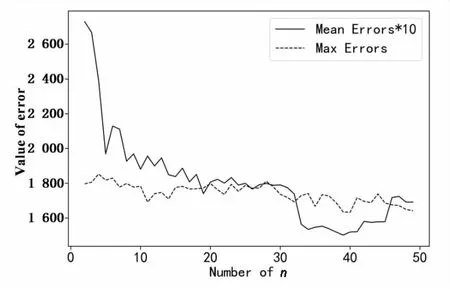
图6 取不同n值时MAE1*10和MAE2的取值

根据划分出来的最优等级个数39,将数据集划分成39份D1,D2,…,D39,每一个子数据集对应一个防控等级,对每一个子数据集建立相应的随机森林,将建好的随机森林进行训练。对于新输入的测试数据M采取以下步骤方法进行预测:

(1)取最接近M时间的训练集中的k个样本(在本例中k为州的个数),作为一天的各个州的数据。

(2)将M的州和k个样本中的州进行逐一比对,找出和M的州匹配的样本S。在实验中州匹配可以由州名直接确定或者由人口数据直接匹配,所以步骤1可以忽略。

(3)确定M的医疗防控能力等级和S的医疗防控能力等级相同,并将该等级作为M的医疗防控能力等级。

(4)用对应的随机森林来对M进行预测得到死亡人数。

采用n=39的情况对模型进行误差处理,最终的拟合结果如图7所示。

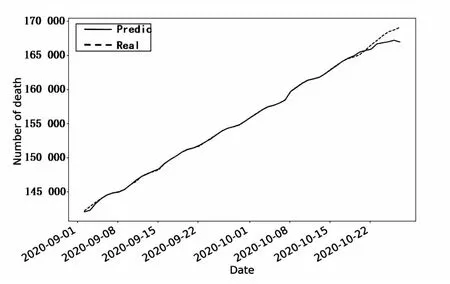
图7 引入衍生特征处理后的拟合结果

对比图3和图7可以发现,在引入衍生特征差异化处理调整参数后,该预测方法兼顾了样本的地区差异性和时间差异性,因此能够起到大幅减小误差的效果。直观地表明样本地区差异和时间差异的问题得到了较好解决。

4 结束语

运用随机森林对疫情数据进行了拟合预测,通过对原始数据样本进行变换衍生出新的特征值来更好地区分样本,起到缩小随机森林预测泛化误差的效果。在对新冠疫情趋势的训练过程中发现,由于各个州之间发展不均衡,医疗条件相差巨大,无法作为一个整体进行预测。在对原始数据分析的基础上,衍生出死亡率作为州医疗条件和防控能力的评价标准,并以此对数据进行分类并单独建立随机森林分类学习。在预测新样本的死亡数时,选用训练地区相近和时间相近的随机森林对新样本进行预测,兼顾了各州原有医疗能力的差异和采取不同防控措施引起的疫情发展的差异,对于其他类似的疫情预测和相近数据的差异化预测具有一定的参考意义。