基于改进灰狼算法的充电桩供电线路规划研究

战彦君,张玲华,2

(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.江苏省通信与网络技术工程研究中心,江苏 南京 210003)

0 引 言

近年来,煤炭、石油、天然气等化石燃料的大量消耗,使得能源危机和环境问题日益严重[1]。为了有效应对,中国提出了碳达峰、碳中和目标,致力于构建以电能为核心的清洁、低碳、高效能源体系,大力推广电动汽车是其中的重要一环。与燃油汽车不同的是,电动汽车续航能力较差,因此要在城市中布设充电桩。由于实际城市中建筑的限制以及区域需求不同,充电桩的分布具有随机性和不均匀性,假如充电桩和电力调度中心之间供电线路规划不合理,必然会大大增加建设成本和电力传输过程中的损耗。为此,研究合适的充电桩供电线路模型,以最高效率和最低成本对充电桩供电十分重要。

受到灰狼围捕和狩猎的行为启发,Mirjalili等人于2014年提出了灰狼算法[2](gray wolf optimization,GWO)。相较于粒子群算法[3]、遗传算法[4]、蚁群算法[5]等经典智能优化算法,该算法具有结构简单、参数少、求解精度高且速度快[6]等优点,被广泛应用于经济调度[7]、作业车间调度[8]、图像分割[9]和云计算资源负荷预测[10]等诸多领域。但是,GWO算法存在易陷入局部最优解、初始种群分布不均匀和后期收敛速度慢[11]等缺点。该文提出一种基于Tent混沌映射[12]和自适应收敛因子的改进灰狼优化算法(ITAGWO),将其应用于城市电动汽车充电桩供电线路规划中。首先,针对初始种群分布不均匀,采用Tent混沌映射来产生种群初始可行解,以丰富种群的多样性;其次,将线性收敛因子改为非线性自适应收敛因子,平衡其局部搜索和全局搜索能力,加快收敛速度;最后,改进灰狼围捕猎物时的位置更新公式,以不同权重采纳三类头狼的经验,并加入随机扰动因子。对区域的充电桩进行供电线路规划仿真,与传统灰狼算法、粒子群算法(particle swarm optimization,PSO)、遗传算法(genetic algorithm,GA)、免疫算法[13](immune algorithm,IA)、模拟退火算法[14](simulated annealing algorithm,SA)、布谷鸟算法[15](cuckoo search algorithm,CSA)、教与学算法[16](teaching-learning-based optimization,TLBO)进行了对比。在到达全局最优解的前提下,该算法迭代次数少、收敛速度快且稳定性好,相比于其他智能算法具有明显优势。

1 模型构建

该文主要提出一种充电桩供电线路规划模型,在连接区域中所有充电桩的同时,以路径最短为目标。模型可以描述为:在区域中有n个充电桩,并且充电桩坐标位置已知,供电线路从其中某一充电桩出发,依次为区域中所有充电桩输电,每个充电桩都只被经过一次。当区域中充电桩数目过多时,单线路输电效率过低,此时将区域分成多个子区域,每个子区域采用一条供电线路将区域内的充电桩遍历,可以显著缩短供电时间,提高充电桩输电效率。为构建适当模型,作以下假设:

(1)不考虑实际的交通道路情况,仅以直线距离为例;

(2)不考虑线路中仅有部分充电桩需要供电的情况,假设每次输电每个充电桩都需要被充电;

(3)假设电力调度中心距离哪个充电桩近,就以该充电桩为起点;

(4)不考虑充电桩需求量超过线路输送容量的情况,假设每次输电都能满足所有充电桩的需求;

(5)当划分子区域时,假设各子区域中的供电线路都与单调度线路模型一致。

1.1 单调度线路模型构建

(1)区域中第i个充电桩和第j个充电桩之间的距离Dij的计算公式为:

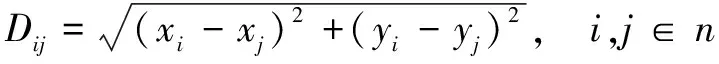
(1)

其中,xi和yi表示充电桩i的横纵坐标;xj和yj表示充电桩j的横纵坐标;n表示区域中的充电桩个数。

(2)定义0-1变量来判断是否经过某个充电桩:

(2)

(3)为了以最小运输成本给充电桩输电,就要使供电线路的总路径长度最小,所以目标函数的函数表示为:

(3)

其中,约束条件表示调度线路必须经过每个充电桩,并且只经过一次。

1.2 多调度线路模型构建

当区域中充电桩数量过多时,为了有效提高输电效率,将区域划分成多个子区域,分多条线路对供电桩进行高效率输电。在充电桩总数为n的情况下,将区域分成p个子区域,第k个子区域中的充电桩个数为xk(k=1,2,…,p)。

(1)在第k个子区域中,第i个充电桩和第j个充电桩之间的距离Dikjk计算公式为:

(4)

其中,xik和yik表示第k个子区域中充电桩i的横纵坐标;xjk和yjk表示第k个子区域中充电桩j的横纵坐标。

(2)定义0-1变量来判断是否经过第k个子区域中某个充电桩。

(5)

(3)要遍历子区域中的每个充电桩,同时供电线路总长度最短,目标函数表达式为:

(6)

其中,p表示所划分的子区域个数;xk表示第k个子区域中充电桩的个数;约束条件表示第k条供电线路必须经过子区域k中每个充电桩,且只经过一次,所有子区域中充电桩总数为m。

2 传统灰狼算法

2.1 灰狼种群的等级制度

灰狼种群具有十分严格的等级制度,狼群具体划分为α狼、β狼、δ狼、ω狼四类[17]。其中α狼是种群中的最高领导者,负责管理种群和各项重要决策事务;β狼的职责是协助α狼做出决策和管理整个种群,传送上级指令并反馈信息;δ狼服从前两类狼的调度命令,从事侦查、放哨等底层管理事务,能力不足或者生病的α狼、β狼也会降级成δ狼;而ω狼是种群的基本组成成员,等级最低且数量最多,需要服从三类头狼的命令,对于维持种群平衡有着不可或缺的作用。

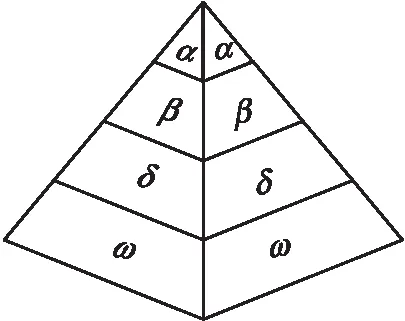
图1 灰狼种群等级金字塔

灰狼狼群的捕猎行为分成跟踪、包围和猎杀三个阶段。首先,灰狼群体会对目标猎物进行追踪;之后,由α狼带领整个狼群对目标猎物进行全方位的包围;最后,α狼指挥最靠近猎物的β狼、δ狼对猎物进行猎杀,若是猎物逃脱,由狼群中其余灰狼继续进行围猎,直到最终捕获猎物。

2.2 灰狼算法GWO

假设搜索空间为D维,数量为N的灰狼组成种群,其中第i只灰狼的位置记为:Xi=(Xi1,Xi2,…,XiD),将种群中适应度值前三个分别记为α狼、β狼和δ狼,种群中其它个体全部记为ω狼。

(1)在跟踪和包围猎物的过程中,相应的数学模型为:

(7)

(8)

(9)

(10)

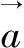
(2)在狼群锁定目标猎物的位置后,α狼会带领β狼和δ狼包围猎物。通常这三类狼对目标猎物的潜在位置更加了解,所以狼群其他成员根据三者的位置判断猎物的位置并不断更新自身位置,向着目标猎物靠近。狼群围猎行为的数学模型如式(11)～式(13)所示:

(11)

(12)

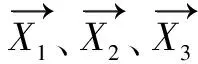
(13)

根据式(13)所求步长,最终确定灰狼个体下一步的更新位置。

3 改进灰狼算法(ITAGWO)

3.1 Tent混沌映射

针对GWO随机产生初始可行解导致的初始种群分布不均匀、物种多样性差的缺陷,采用Tent混沌映射的方法产生初始种群,其良好的多样性和遍历性有效提高了求解精度和收敛速度。Tent映射也即帐篷映射,是一种分段的线性映射,因其函数图像酷似帐篷而得名,其函数表示如下:

(14)

由于u=1/2时,Tent映射是具有均匀分布的典型序列,对不同的参数有近似一致的分布密度,因而该文引用u=1/2的Tent映射公式,如式(15)所示:

(15)

3.2 非线性收敛因子

在灰狼算法中,收敛因子a的选取决定算法的局部和全局搜索能力[18]。传统灰狼算法的收敛因子是从2线性递减到0的,而在实际优化问题中灰狼算法的搜索过程比较复杂,线性递减的收敛因子导致算法的搜索能力弱[19]。该文采用非线性递减的方式改进收敛因子[20]:前期递减速度慢,较大的a值增强全局搜索能力,避免陷入局部最优解;后期收敛速度慢,较小的a值增强局部搜索能力 ,加快收敛速度。这种非线性收敛机制可以协调灰狼算法的局部和全局搜索能力,并且a值切换具备自适应性。改进收敛因子表达式如式(16)所示:

(16)

其中,k为调节系数,它的取值决定着a随着迭代次数增加而递减的速度,该文取为e[6];t为当前迭代次数;tmax为最大迭代次数。

3.3 随机扰动

传统灰狼算法中,ω狼的位置更新是等权重地参考三类头狼的位置信息,在搜索后期所有灰狼都会向α狼、β狼、δ狼附近区域靠拢,这样极易陷入局部最优,影响算法的收敛速度。该文采用的位置更新公式采用不同的权重参考三类头狼的位置信息,对级别越高的狼参考权重相应越大,以加快收敛速度;并加入了随机扰动以防止陷入局部最优解,其公式表达如下:

(17)

3.4 改进灰狼算法流程

改进灰狼算法流程如图2所示。

图2 改进灰狼算法流程

4 仿真实验及分析

4.1 实验参数设置

实验仿真软件为Matlab R2018b。参照元启发式算法比较文献[21]和各算法的参考文献中对实验参数的设置,结合实际实验过程中算法的性能和收敛效果,对各个算法的参数设置如下:GWO和ITAGWO的种群大小为100;CSA的种群大小为100,鸟蛋被发现概率为0.3,步长因子α为0.015,莱维飞行中的β因子为1;PSO中粒子数量为500,个体学习因子为0.1,社会学习因子为0.075,惯性因子为1;IA的抗体种群个数为100,免疫选择比例为20%,抗体克隆扩增倍数为5,种群刷新比例为抗体种群的30%;SA的初始温度为1 000,终止温度为1e-3,降温因数为0.9,Metropolis准则链长为200,种群大小为100;GA的种群规模为100,交叉概率为0.7,变异概率为0.001;TLBO的种群大小为100。查阅群智能算法相关文献发现,其迭代次数一般设置为100～500,结合实验迭代终止时次数均在50以内的情况,考虑到未来更复杂区域和更庞大数量充电桩的场景,该文所有算法的终止迭代次数均为300次,种群搜索维度为10。

假设空间中存在一个100 km*100 km的正方形区域,坐标范围为(0,0)到(100,100),将空间划分成四个子区域,每个子区域中有10个充电桩,以区域中充电桩全部连接时总线路长度最小为目标进行实例仿真,各区域充电桩的坐标见表1。

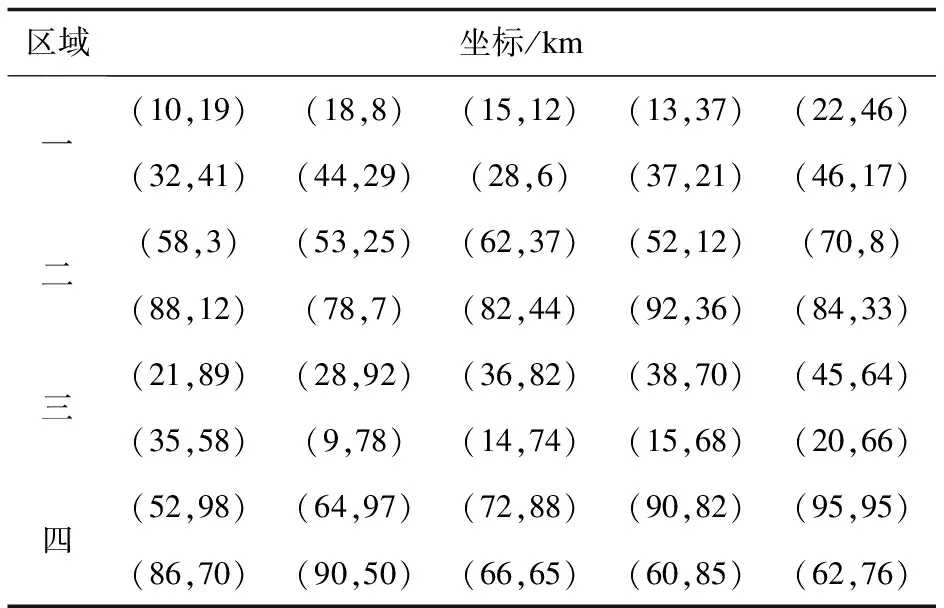
表1 各区域充电桩坐标

区域中所有充电桩的坐标位置分布情况见图3。

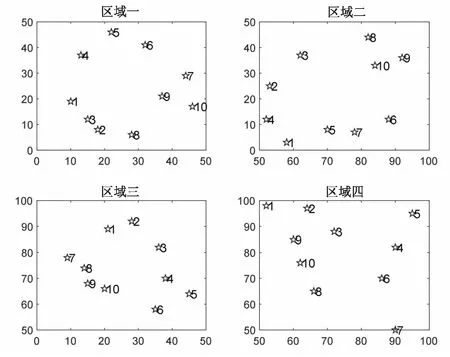
图3 区域充电桩位置分布

4.2 算法对比分析

利用ITAGWO和七种比较算法对表1中的充电桩仿真五次,虽然各种算法求得最优解的迭代次数不同,但其所求的最优解是相同的,且其最优供电线路也一致。各算法五次仿真的平均迭代次数和最优迭代次数见表2,最优供电线路规划方案见图4。

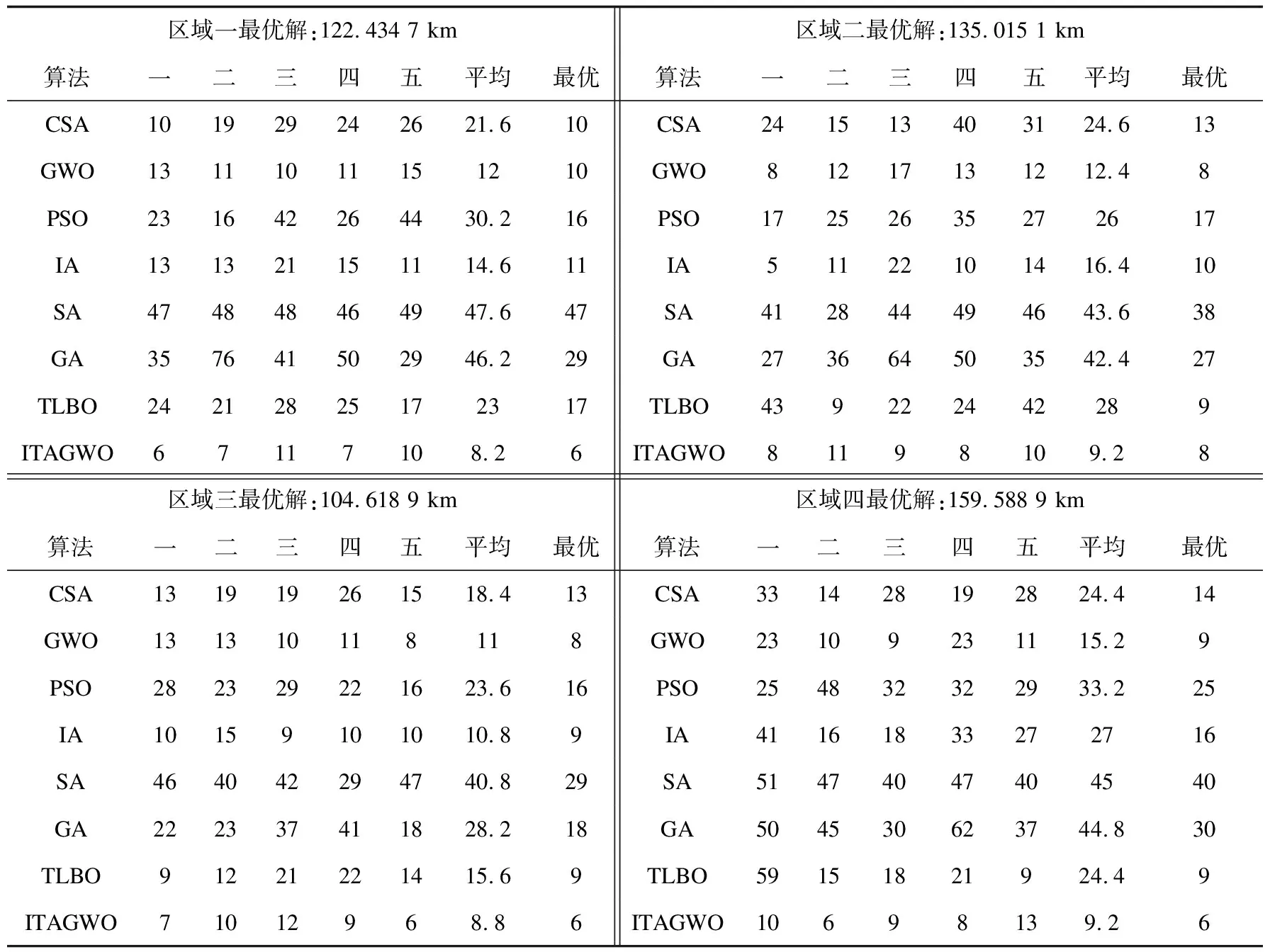
表2 各算法在四区域的迭代次数

图4 各区域能源调度路线规划

由表2,ITAGWO与其他七种比较智能算法都可以找到最优解,但ITAGWO的迭代次数更少,收敛速度更快,且迭代次数间方差较小,更具稳定性。

在区域一,各比较算法中GWO的平均迭代次数和最优迭代次数均最少,ITAGWO的平均迭代次数和最优迭代次数分别比GWO提高了31.6%和40%;在区域二,各比较算法中GWO的平均迭代次数和最优迭代次数均最少,ITAGWO的最优迭代次数虽然与GWO一致,但平均迭代次数提高了25.8%;在区域三,各比较算法中IA的平均迭代次数最少,GWO的最优迭代次数最少,ITAGWO的平均迭代次数比IA提高了18.5%,最优迭代次数比GWO提高25%;在区域四,各比较算法中GWO的平均迭代次数和最优迭代次数均最少,ITAGWO的平均迭代次数和最优迭代次数分别比GWO提高了39.5%和33.4%。

5 结束语

针对城市中电动汽车充电桩分布的随机性和不均匀性,将灰狼算法用于其供电线路规划。GWO算法存在易陷入局部最优解、初始种群分布不均匀和后期收敛速度慢等缺点,该文提出一种基于Tent混沌映射和自适应收敛因子的ITAGWO算法。实例仿真结果表明,在到达最优解的前提下,ITAGWO比其余七种算法的迭代次数少、收敛速度快且稳定性好,可以很好地应用于充电桩供电线路规划。