基于AADL模型航空安全软件可信性度量方法

刘歆宁,康 玲

(大连东软信息学院 软件工程系,辽宁 大连 116023)

0 引 言

近年来,随着安全关键软件在航空航天领域的广泛应用,安全关键软件在兼顾高可靠性和高安全性的需求不断提高,同时安全关键软件也面临着越来越复杂的窘境。近年来,模型驱动开发方法逐渐成为安全关键软件开发方法的一种发展趋势,例如国际民航领域使用的机载系统适航审定中的软件开发标准DO-178C就将模型驱动和形式化方法作为其核心标准的重要技术补充[1]。

美国自动机协会(Society of Automotive Engineers,SAE)体系结构描述语言附属委员会、嵌入式计算系统委员会及航空电子系统公司于2004年10月提出了专门针对安全关键的嵌入式实时系统的软硬件分析设计语言─体系结构分析与设计语言(Architecture Analysis and Design Language,AADL)[2]。AADL能够对嵌入式软件的功能和非功能属性进行建模和分析,是控制系统复杂性和保证软件质量的重要手段。目前,对基于AADL模型的软件可信性度量与分析,主要集中于将AADL故障模型附件转换为随机Petri网或故障树的方法[3-5],以实现对模型的可靠性分析,因此,研究全面的可信性的度量与分析方法是十分必要的。

基于以上考虑,该文提出了基于AADL模型的软件可信性的度量与分析技术的研究这一课题。该研究能够在软件开发的早期阶段对基于AADL模型的软件可信性进行度量、分析与评估,从而提高软件的质量。该文研究AADL模型特点,从AADL模型中提取可度量的指标并建立度量模型,将对象软件度量方法、软件体系结构度量方法、Markov分析方法及熵理论方法应用于各个度量指标的计算之中,对度量结果进行分析,并根据所建立的软件可信性度量模型,采用适合的评估方法对软件可信性的度量结果进行评估。最终实现一个基于AADL模型的软件可信性度量与评估的工具,该工具能够分析已有软件的AADL模型,提取模型中的可信性度量指标并计算指标值,对度量结果进行简单的分析并最终对度量结果进行评估。

1 基础理论

1.1 AADL标准及扩展附件

为了更好地设计与分析嵌入式实时系统的软、硬件体系结构及功能与非功能属性,嵌入式实时系统体系结构分析与设计语言(AADL)被提出。AADL标准由核心语言标准和扩展附件标准组成,是一种基于组件的建模语言,采用结构化的描述来对嵌入式系统的软硬件进行统一建模。

AADL的扩展附件是对AADL核心标准的补充描述,它们可以嵌入在AADL核心语言的包以及组件实现中。其中比较重要和常用的附件是故障模型附件EMA(Error Model Annex)和行为附件BA(Behavior Annex)。AADL故障模型由类型和实现两部分组成。故障模型类型(error model type)定义了故障状态(error states)、故障事件(error events)以及故障传播(error propagations)等,其中故障事件是针对组件内部的,故障传播则是针对组件之间交互的[6-7]。

1.2 软件可信性度量与分析技术

对于可信性的概念,不同的人员有不同的认识。微软的比尔盖茨提出了可信计算的4个基本属性[8],即可靠性、安全性、保密性和商业诚信。美国科学与技术委员会则认为:可信系统要求具有很多特性,包括功能正确性、防危性、容错性、实时性和安全性。陈火旺院士提出了高可信性质的概念[9],认为软件系统的可信性质是指该系统需要满足的关键性质。国际标准ISO/IEC 9126:2001[10]定义了软件的质量模型,该模型将软件质量属性划分为6个特性:功能性、可靠性、易用性、效率、维护性和可移植性。刘晗从源代码证据入手,建立面向航天领域的嵌入式软件可信度量评估方法[11]。

1.3 模糊综合评价法

模糊综合评价法[12]是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价[12]。此方法具有结果清晰、系统性强的特点,能较好地解决模糊的、难以量化以及各种非确定性的问题。

1.4 基于AADL模型软件可信性度量系统研究框架

目前基于AADL模型的度量与分析主要集中在利用AADL故障模型的可靠性度量,对AADL核心模型的度量涉猎极少。AADL核心标准描述了AADL的功能和非功能属性,这些属性直接影响到软件的可信性,因此对其进行度量是十分必要的。并且目前对AADL模型的度量主要是从可靠性和安全性两个角度进行,而仅这两个方面是不能全面反映软件在可信性方面存在的问题的。同时,缺少基于AADL模型的软件可信性度量与评估工具。

2 基于AADL航空软件可信性度量

2.1 核心模型的软件可信性度量方法

2.1.1 AADL核心模型复杂性度量

软件复杂度度量作为软件工程的重要组成部分,可为高质量软件的研究提供支撑[13]。组件之间存在依赖关系,则被依赖组件的变化将影响到依赖于它的组件。显然,组件之间的依赖关系越多,组件之间的相互影响越大,系统复杂性越高。

模式modes是AADL核心模型所特有的,它用来描述运行时体系结构的动态演化。通过分析模式modes的特点,可得到如下几个度量指标:

指标一:平均模式转换总数(Average Number of Mode Transitions,ANMT)。

定义NMT(i)为第i个有模式转换组件的模式转换总数,则ANMT的计算方法如公式(1)所示:

(1)

其中,n为有模式转换的组件的总数。

度量原则:ANMT越大,组件在不同的模式之间转换次数越多,则系统的复杂性越高。

指标二:系统所含有模式转换的子组件数(Number of Modes in System,NMS)。

在AADL核心模型中,使用in modes语句指定一个子组件在模式modes中是活跃的,则NMS为所有含有模式转换的子组件总数。

度量原则:NMS越大,则该子组件的职责越多,整个系统也就越复杂。

由本节度量指标的计算方法,得到计算模式复杂性所涉及的AADL核心模型的元素与所使用的度量方法的对应关系,如表1所示。

表1 模式复杂性度量与度量方法对应关系

AADL核心模型中的包与面向对象中的包的概念相似,通过引入一个独一无二名字空间,提供了一个方式来组织组件类型、组件实现及特性组等元素。本节通过对AADL核心模型中包的分析,从中提取出以下几个度量指标:

指标一:平均包中关联关系的总数(Average Number of Associations in a Package,ANAP)。

在AADL核心模型的每个包中,组件及组件之间的连接connections描述了系统的组成和结构,体现了软件体系结构的主要信息。从这个方面考虑,定义NAP为包中connections的总数,则ANAP的计算方法如公式(2)所示:

(2)

其中,NAP(i)为第i个包的NAP值,n为包总数。

度量原则:ANAP越大,包复杂性越高。

指标二:平均包中的关联关系数(NAP)与包中组件的数目的比值(Average Number of Associations vs.Component in a Package,ANAVCP)。

包中平均每个组件的关联关系越多,包就越复杂,从而导致包越难理解和维护,则:

(3)

其中,NAP为包中的关联数,compn为包中的组件数,则ANAVCP的计算方法如公式(4)所示:

(4)

其中,NAVCP(i)为第i个包的NAVCP值,n为包的数目。

度量原则:ANAVCP越大,包复杂性越高。

由本节度量指标的计算方法,得到计算包复杂性所涉及的AADL核心模型的元素与所使用的度量方法的对应关系,如表2所示。

表2 包复杂性度量与度量方法对应关系

2.1.2 AADL核心模型耦合性度量

耦合性度量是软件结构中各个模块之间联系紧密程度的度量。耦合性越高表示该元素与其它元素的调用关系越多,则该元素设计改动的敏感性越明显,这给软件的维护和修改造成了困难[14]。因此,组件间的耦合性可用来度量组件的可理解性、可靠性、可维护性和可用性等。本部分针对AADL核心模型的特点,分别从连接connections、特性features、继承extends和包package的角度考虑,提取出以下度量指标:

指标一:平均继承耦合(Average Extends Coupling,AEC)。

定义EC(i)为系统中所有从组件i继承而来的组件的信息量的集合,则AEC的计算方法如公式(5)所示:

(5)

其中,n为继承父组件的个数。

度量原则:AEC越大,继承父组件与继承子组件之间的关联越密切,耦合度越高。

指标二:包间耦合因子(Coupling Factor between Packages,CFP)。

如果包ci使用了包cj中的属性或特性,则isclient(ci,cj)=1,否则isclient(ci,cj)=0,则CFP的计算方法如公式(6)所示:

(6)

其中,TC表示系统的包的总数。

度量原则:包间耦合因子越大,包之间的关联越密切,耦合度越高。

由本节度量指标的计算方法,得到计算耦合性所涉及的AADL核心模型的元素与所使用的度量方法的对应关系如表3所示。

表3 耦合性度量与度量方法对应关系

2.2 基于AADL故障模型的软件可信性度量方法

AADL故障模型附件是一种半形式化的语言,直接对基于AADL故障模型的软件进行可信性度量是比较困难的,而形式化方法可以对语义进行更加精细的描述,能够更好地用于模型的可信性分析,为此需要考虑对AADL故障模型进行形式化的语义描述。

2.2.1 AADL故障模型到Markov模型的转化规则

通过对AADL故障模型的研究可知,AADL故障模型同Markov模型相同,都是指明了状态和状态的转移,即故障状态及故障状态之间的转移,一个故障状态转移到其他故障状态的概率值由Occurrence属性指明。将AADL故障模型转换为Markov模型,是模型转换的过程,通过对AADL故障模型和Markov模型进行分析,得到将AADL故障模型转化为Markov模型的整体规则是:将AADL故障模型中组件的故障状态对应于Markov模型中的状态,故障状态迁移对应于Markov模型中的状态迁移,故障状态迁移的Occurrence属性值对应于Markov模型中状态迁移的概率。为了体现AADL故障模型的相关信息,在传统的Markov模型的形式化定义的基础上,提出了一种扩展的Markov链:

定义1 扩展Markov链(Expanded Markov Chain,EMC):EMC=(S,S0,∑,P,Q),其中:

(1)S是组件的故障状态的集合,是一个有限集,可表示成:S={S0,S1,…,Sn};

(2)S0是组件的初始故障状态,一般是无故障状态,且S0∈S;

(3)∑是故障状态转移集合,每一个集合用一个两元组表示:{TriggerType,TriggerName},其中TriggerType是触发故障状态转移的类型,此类型包括故障事件error event和故障传播error propagation两种,该文只考虑故障事件error event,对于故障传播error propagation在以后的研究中再将其考虑在内,故此处的类型均为故障事件error event ,TriggerName是触发故障状态转移的事件的名字;

(4)P是故障状态之间转移的概率集,每一个概率集定义为一个三元组:{Probability,ProbabilityType,ProbabilityDefinition},其中Probability是故障状态转移的概率,ProbabilityType指明是失效率还是恢复率,分别用failure rate和recovery rate表示;ProbabilityDefinition指明转移的概率是服从1-e-λ的指数分布,还是一个0～1的小数值,分别用poisson和fixed表示;

(5)Q表示故障状态之间转移的关系,即:

S×∑→S

根据定义1的基于AADL故障模型的扩展Markov链的形式化描述,将AADL故障模型的各个元素与扩展的Markov模型中的各个元素相对应,得到AADL故障模型到扩展Markov链的对应关系,如表4所示。

表4 AADL故障模型的元素与扩展Markov链的元素的对应关系

图1是一个组件的AADL故障模型实例,将它用上文提出的转换规则转换为扩展的Markov链如下:

图1 故障模型实例

EMC={S,Error_Free,∑,P,Q},其中:

S={Error_Free,Erroneous,Failed};

∑={∑1,∑2,∑3,∑4},其中∑1={error event,Perm_Falult},∑2={error event,Temp_Fault },∑3={error event,Restart},∑4={error event,Recover}

P={P1,P2,P3,P4},其中P1={0.125,failure rate,fixed},P2={0.175,failure rate,fixed},P3={0.8,recovery rate,fixed},P4={0.9,recovery rate,fixed}

Q={Error_Free×∑1→Failed,Error_Free×∑2→Erroneous,Failed×∑3→Error_Free,Erroneous×∑4→Error_Free }

2.2.2 AADL故障模型的可信性度量

从AADL故障模型的Markov形式化描述中,可以获取从无故障状态到故障状态的失效率,以及故障状态到无故障状态的恢复率,从而得到一步状态转移概率矩阵。AADL故障模型之间的状态转移满足Markov链的齐次性,因此由AADL故障模型转换的扩展Markov链也是齐次的,因此可采用Markov分析方法预测组件在长期运行后的失效率。以图1的AADL故障模型为例,该模型有一个初始无故障状态和两个故障状态,可转换为三态的Markov链,其一步状态转移概率矩阵P如公式(7)所示:

(7)

设稳态状态向量为Y(3)={y1,y2,y3},其中y1为组件长期运行时处于正常状态的概率,y2和y3分别为组件长期运行时处于两个故障状态的概率,则y2+y3为组件长期运行时的总体失效率,即稳态失效率。由方程组(8)得:

(8)

计算出单个组件的相关度量指标之后,通过指定各个组件的权重,可以得到系统的相关的度量指标如下:

(1)系统的稳态失效率为:

(9)

其中,λi为第i个组件的稳态失效率,Simpi为第i个组件的权重,且该指标与软件可信性是负相关。

(2)系统的恢复率为:

(10)

其中,μi为第i个组件的恢复率,Simpi为第i个组件的权重,μi的值通过从第i个组件的AADL核心模型中的属性集中提取出来,且该指标与软件可信性是正相关。

(3)系统的MTBF为:

(11)

其中,MTBFi为第i个组件的MTBF,Simpi为第i个组件的权重,且该指标与软件可信性是正相关。

(4)通过Markov分析方法,可以求出系统的可用度。可用度是指系统在任一随机时刻处于工作或可使用状态的概率,它是系统效能的重要因素。当Markov链是齐次的,且系统的稳态失效率和恢复率分别为λsum和μsum时,系统的瞬态可用度为:

(12)

当t→∞时,可得系统的稳态可用度为:

(13)

3 基于AADL模型的软件可信性度量模型与评估方法

在对软件进行可信性评估之前,可以对软件可信性进行一些简单的分析,总结2.1与2.2中AADL模型可信性度量的研究成果,得到基于AADL模型的质量属性相关的度量指标列表,如表5所示。

表5 AADL质量属性相关的指标列表

除了对度量结果进行如上的定性分析,还可以利用AADL模型中的属性集property sets对度量结果进行定量分析。AADL模型中的属性properties定义了组件以及组件描述的约束,用户可根据自己的需求对属性properties进行扩展,这些属性主要定义了系统的质量属性方面的约束,文中的用户可以为设计人员或者相关领域专家。

将各个度量指标值与属性集中相应属性的属性值相比较,有如下两种情况:

(1)度量指标与可信属性成正相关时:当度量指标值大于属性值时,该度量指标值满足用户需求;当度量指标值小于属性值时,该度量指标不满足用户需求;

(2)度量指标与可信属性成负相关时:当度量指标值小于属性值时,该度量指标值满足用户需求;当度量指标值大于属性值时,该度量指标不满足用户需求。

这样,设计人员可以根据分析结果对所设计的模型进行修改,使模型尽可能地满足用户的需求。

4 工具实现及案例分析

4.1 工具实现

基于AADL模型软件可信性度量与评估工具的目标是对基于AADL模型的软件可信性进行度量、分析与评估。该工具组件给予基于AADL模型的软件可信性度量、分析与评估的全方位支持,能够在软件开发早期为相关人员做出决策提供参考。

该工具包括基于AADL模型的软件可信性度量模型的定制、AADL数据采集、AADL模型的可信性度量与分析及AADL模型的可信性评估四个模块,见图2。工具首先需要通过数据采集模块采集度量数据,解析以XML形式表示的AADL模型,从模型文件中提取被度量组件及组件之间的关系,以实现对这些被度量组件的解析。

图2 基于AADL模型的软件可信性度量与评估系统体系结构

AADL模型度量与分析模块以定制的可信性度量模型为依托,统计采集到的数据,度量与分析统计的结果可以反映出软件的可信性。系统对采集的数据进行度量后,将度量的指标值传递给软件可信性评估模块。

4.2 案例分析

本节以一个应用实例来详细介绍基于AADL模型的软件可信性度量与评估工具的操作步骤和实验结果。该课题以AADL官方网站上的航空电子系统Avionics_System为例。针对该航空电子系统Avionics_System中的主要组件,根据以往的经验,给出了相应的故障模型,并给出了属性集。图3显示了航空电子系统Avionics_System的图形表示,由于系统中的端口交互较为复杂,图3只给出了系统的主要结构。

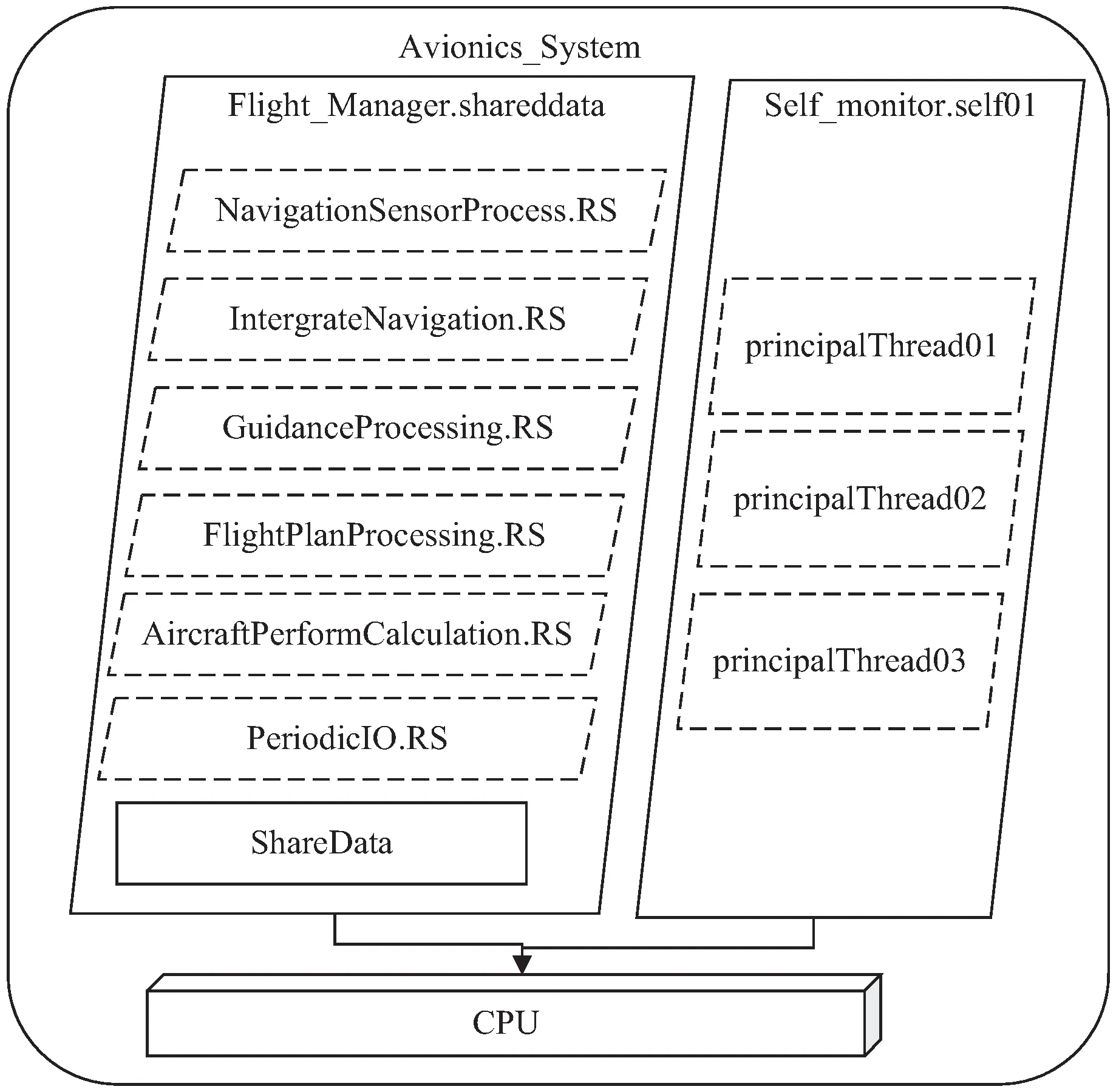
图3 航空电子系统模型

进入基于AADL模型的软件可信性度量与评估工具主界面。本节以航空电子系统Avionics_System为例,按照可信性度量模型定制->AADL数据采集->AADL模型度量与分析->AADL模型评估的操作步骤对该工具进行介绍,并对系统运行的结果进行分析和总结。

(1)可信性度量模型定制。

通过系统结构树中的可信性度量模型定制节点,进入基于AADL模型的软件可信性度量与评估工具的可信性度量模型定制功能,用户可以根据实际需要或自身经验定制软件的度量模型。

(2)AADL模型数据采集。

软件可信性度量模型定制完成后,进入AADL数据采集界面,该模块包括3个子模块:AADL核心模型数据采集、AADL故障模型数据采集和AADL属性集采集。

(3)AADL模型度量与分析。

通过采集AADL模型数据并对AADL模型进行解析之后,该工具可以对AADL模型进行度量与分析,该度量与分析由两方面组成,即AADL核心模型度量与分析和AADL故障模型度量与分析。

(4)AADL模型评估。

根据评价矩阵建立的方法,该部分针对各个度量指标设定隶属函数中的μ值,从而计算出各个度量指标在各个可信等级上的隶属度,进而得到该航空电子系统Avionics_System隶属于各个可信等级的结果。从图4中的结果可以看出,评估结果对应可信第一级“肯定可信”隶属度最大,第二、三级“很可能可信”的隶属度明显低于第一级,第四、五级的隶属度很低,该结果表明该航空电子系统Avionics_System属于五个可信等级中的第一等级。

图4 航空电子系统可信性评估结果

若对该飞行Avionics_System的AADL模型的某一方面进行修改,如修改该系统的故障模型的概率转移值,其他条件不变,最终得到软件可信等级隶属度和最终系统可信性评估结果。从图5中可以看到:与修改之前相比,该系统在第一等级的隶属度有所降低,在第四、五级的隶属度有显著增加。这说明对被评估模型的任意一个方面修改都能够影响软件可信性评估结果,说明该工具是敏感的。

图5 修改模型后系统可信性评估结果

(5)实验结果。

该工具实现了对基于航空电子系统Avionics_System的AADL模型进行可信性度量、分析与评估的功能,对实验结果的分析表明:利用该工具可以对基于AADL模型的软件进行可信性度量、分析与评估,得到的度量与评估结果可供设计人员参考,以便在软件开发早期发现软件可信性方面存在的问题,从而提高软件的质量。利用该工具对软件进行可信性度量、分析与评估的步骤简单便捷,用户可以很快熟练使用该工具。

5 结束语

基于AADL的核心语义和AADL故障模型,提出了一种软件可信性度量与评估方法,由于时间和工作量的限制,方法的研究与工具的实现还存在不足,进一步的工作应该从以下几个方面展开:

(1)对基于AADL故障模型的度量进行更深入的研究,将其转换为其他形式化模型以提取更多体现软件可信属性的度量指标。

(2)对软件可信性进行评估时,存在历史数据严重不足的问题,因此公式的参数可能存在不准确的问题,下一步将收集历史数据来进一步验证公式。

(3)对AADL的行为附件behavior annex进行研究,提取出可度量的指标,完善基于AADL模型的软件可信性度量与分析模型的指标体系,从而能够更全面且充分地对软件可信性进行度量与评估。