例析整体代换在一道三角函数问题中的运用

汪海鹏

三角函数图像性质问题一直是高考数学试题中的常考问题，在破解此类问题时，经常用到“整体代换”的思想方法.整体代换方法可以实现化繁为简、简便运算，对一些难度较高的三角函数问题可以达到事半功倍的效果.本文结合实例探析“整体代换”在三角函数问题中的应用.

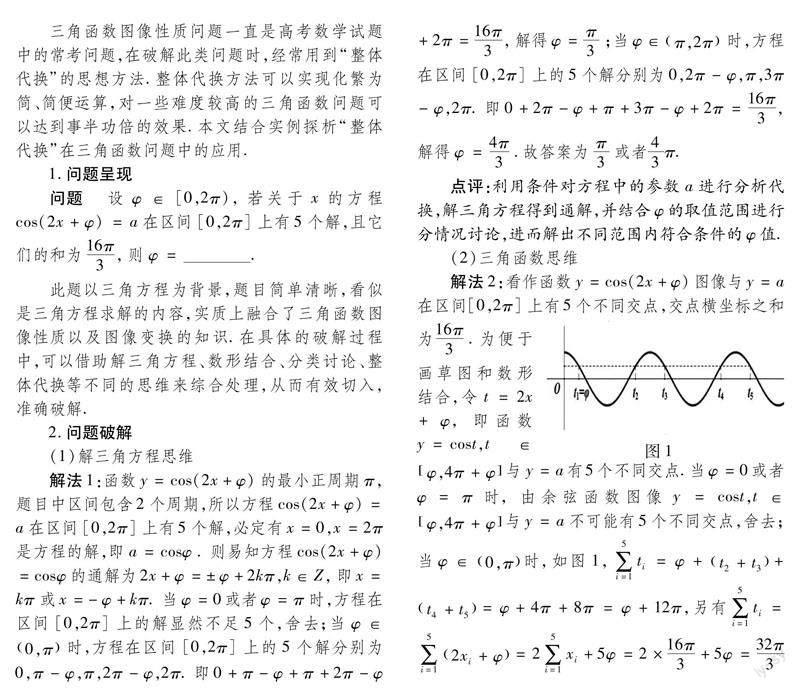
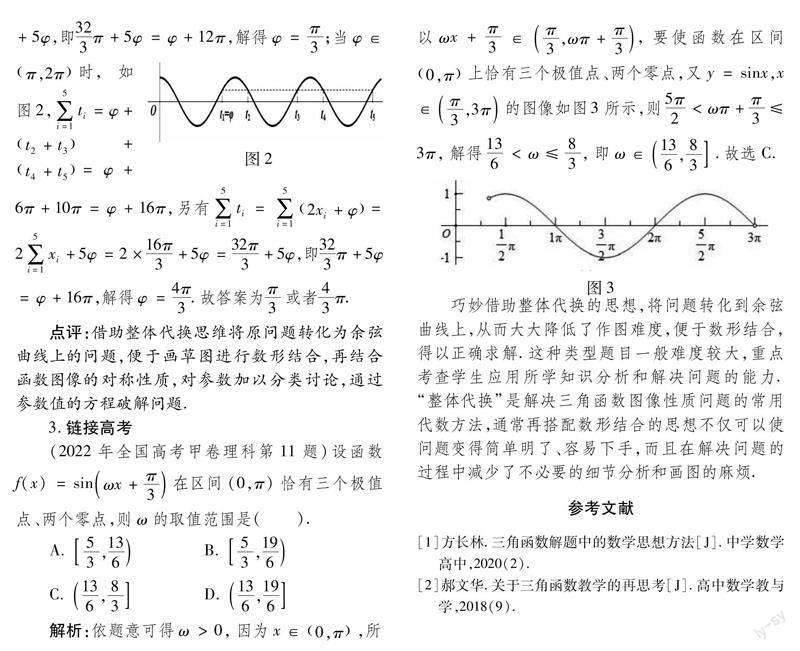
巧妙借助整体代换的思想，将问题转化到余弦曲线上，从而大大降低了作图难度，便于数形结合，得以正确求解.这种类型题目一般难度较大，重点考查学生应用所学知识分析和解决问题的能力.“整体代换”是解决三角函数图像性质问题的常用代数方法，通常再搭配数形结合的思想不仅可以使问题变得简单明了、容易下手，而且在解決问题的过程中减少了不必要的细节分析和画图的麻烦.

参考文献

［1］方长林.三角函数解题中的数学思想方法［J］.中学数学高中，2020（2）.

［2］郝文华.关于三角函数教学的再思考［J］.高中数学教与学，2018（9）.