动压气浮永磁同步电机高稳定性转速控制

李玉猛, 马官营, 惠 欣, 朱梦如

（北京控制工程研究所, 北京 100094）

0 引言

因运转起来无机械接触, 动压气浮电机被广泛应用于长寿命、高可靠液浮陀螺仪［1］中。 液浮陀螺仪基本都采用了磁滞电机, 该型电机的优点是驱动控制简单, 缺点是功耗大, 这限制了液浮陀螺仪精度的进一步提高。 永磁同步电机因工作效率高、功率密度大而在工业中被广泛应用, 并在高精度陀螺仪中逐渐被采用。 与磁滞电机相比,永磁同步电机的控制较为复杂, 其换相控制需要转子位置信息。 因受陀螺仪体积和导电游丝数目的约束, 其内部无法安装位置传感器, 所以陀螺动压气浮永磁同步电机均采用了无位置传感器控制方法。

因不需要安装位置传感器, 永磁同步电机无传感器控制方案降低了系统的复杂性和使用成本,因而备受关注。 其中, 研究较多的方法主要有:滑模观测器法［2-3］、Kalman 滤波法［4］、模型参考自适应法［5］、高频信号注入法［6-7］等。 文献［2］提出了一种扩展滑模观测器, 将反电势估计值反馈至定子电流观测器中, 同时采用饱和函数替代开关函数, 有效地解决了传统滑模函数观测器存在的抖动问题。 针对数字计算产生的转子位置估计延时问题, 文献［3］设计了一种延时抑制滑模观测器,通过在一个开关周期内进行双采样, 实现了电流的前置补偿, 经过补偿后电机转子位置估计精度和控制性能得到提高。 文献［4］提出了一种基于迭代容积Kalman 滤波来估计电机转速和转子位置的方法, 与传统Kalman 滤波器相比, 该方法具有估计精度高、抗负载变化干扰强的优点。 文献［5］研究了一种新型模型参考自适应控制方法, 利用电机反电势重构和分段PI 调节器实现了永磁同步电机在高低速全范围内的稳定运行。 文献［6］提出了一种基于补偿矩阵的高频注入转子位置估计方法,解决了电感矩阵计算转子位置存在的过程繁琐、计算量大的问题, 改善了无传感器控制在低速时的动态性能。 相似地, 为了增强无传感器低速控制性能, 在基于磁通模型的自适应位置观测器基础上, 文献［7］设计了一种包括除法器和低通滤波器的相电压测量回路, 同时补偿硬件滤波器产生的相位延迟和幅值衰减, 并通过试验验证了措施的有效性。 虽然前三种无传感器方法取得了良好的控制效果, 但计算量较大, 工程化实现上较为困难。 与前三种方法相比, 高频信号注入法实现起来相对简单, 但要求转子磁场具有或能够实现凸极性, 因此不适用于定子无铁芯、隐极式陀螺动压气浮永磁同步电机。 此外, 上述无传感器控制方法在很大程度上只关注了转子位置估计的准确性、电机低速下的控制性能以及转速运行范围,而对高转速下的稳定性研究较少。

电机为陀螺仪提供角动量, 其转速平稳性直接影响陀螺仪的测量精度, 因此电机转速控制的目标是获得尽可能高的转速稳定性。 当前, 永磁电机的高稳定转速控制大多采用了锁相环控制方法［8-9］。 文献［8］以晶振输出的高精度脉冲信号为基准对整形后的电机反电势信号进行锁频, 实现了陀螺无刷永磁电机的高稳定性恒速控制, 但电机的动态性能难以保证。

陀螺动压气浮永磁同步电机工作时转速一般在20000r/min 以上, 要实现无传感器高转速高稳定性控制, 转子位置估计必须实时。 因此, 本文设计了基于锁相环的转子位置估计器对反电势过零脉冲信号进行倍频计数来获取转子位置, 保证了位置估计的实时性, 且工程上易于实现。 陀螺电机高速运行时主要克服外部气流产生的阻力,且在正常工作条件下转速是恒定的, 因此受到的阻力矩为恒值, 而电机输出转矩的平稳性也将直接影响转速的稳定性。 针对永磁同步电机的工作特点, 本文提出了一种正弦波线性驱动来减小电机转矩波动; 同时建立了电流环和转速环构成的电机双闭环控制系统, 来提高电机的动态响应特性, 增强系统的抗负载扰动能力。

1 锁相环转子位置估计器

在永磁同步电机众多电气参数中, 反电势是一个比较稳定的参数, 基本不受外部环境影响,因此利用反电势来估计电机转子位置具有很高的准确性。 从反电势波形与转子位置对应关系看,其过零位置代表着转子的一个电气零位。 锁相环属于一种闭环控制系统, 它能够将反馈信号与参考信号进行频率锁定, 同时保持它们之间的相位差恒定, 因而被广泛应用于数字信号处理。 本文通过锁相环对动压气浮永磁同步电机的反电势过零脉冲信号进行频率倍频, 然后再计数来获取转子位置信息, 同时使倍频信号和过零脉冲信号的上升沿保持对齐, 即相位差保持恒定。

基于锁相环的转子位置估计器组成如图1 所示, 主要包括两大部分: 一部分是外围硬件电路,包括反电势拾取电路和过零比较器; 另一部分是FPGA 内部编程实现模块, 包括锁相环、上升沿判别器和计数器。 反电势拾取电路的作用是从电机端电压信号中消除定子电阻压降来获取反电势信号; 比较器的作用是将反电势信号与中性点参考信号进行比较, 来得到过零脉冲信号; 锁相环对反电势过零脉冲信号进行频率倍频, 同时将倍频信号上升沿与反电势过零脉冲信号上升沿锁定;计数器通过对倍频信号的上升沿进行计数, 来获取转子位置。 为了得到转子电气零位信息, 在每个过零信号的上升沿需要对计数器进行一次清零。

利用VHDL 语言编程设计了锁相环、过零脉冲上升沿判别器和计数器, 其RTL 实现框图如图2所示。

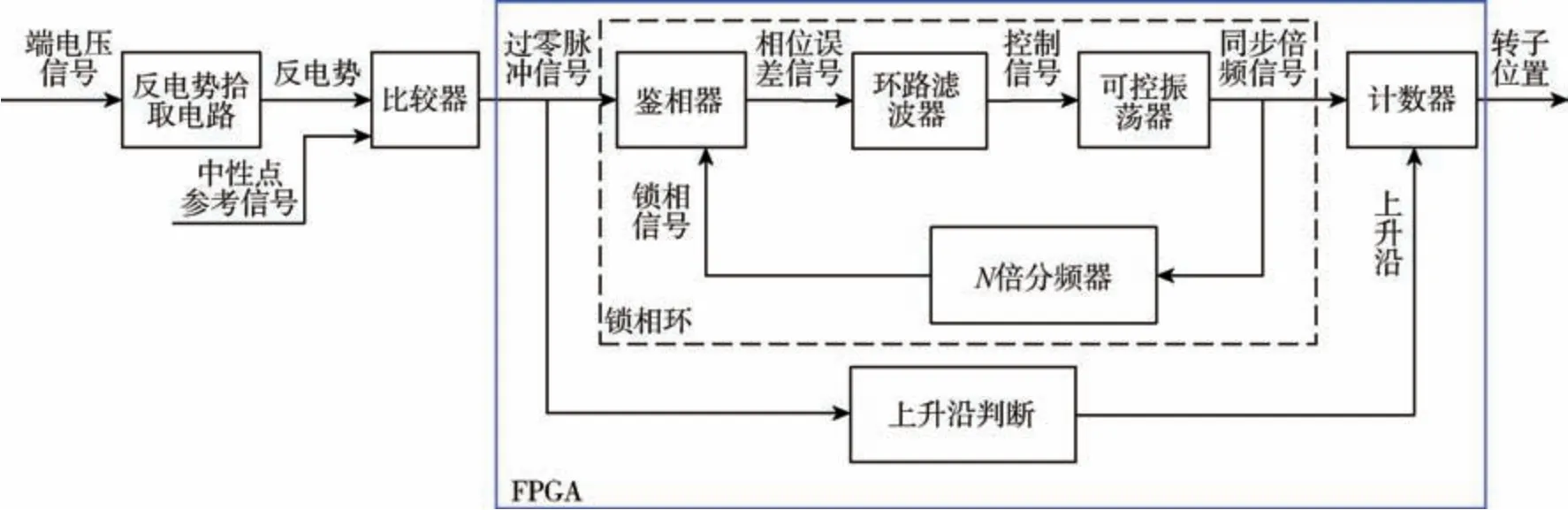
图1 锁相环转子位置估计器组成Fig.1 Constitution of PLL rotor position estimator

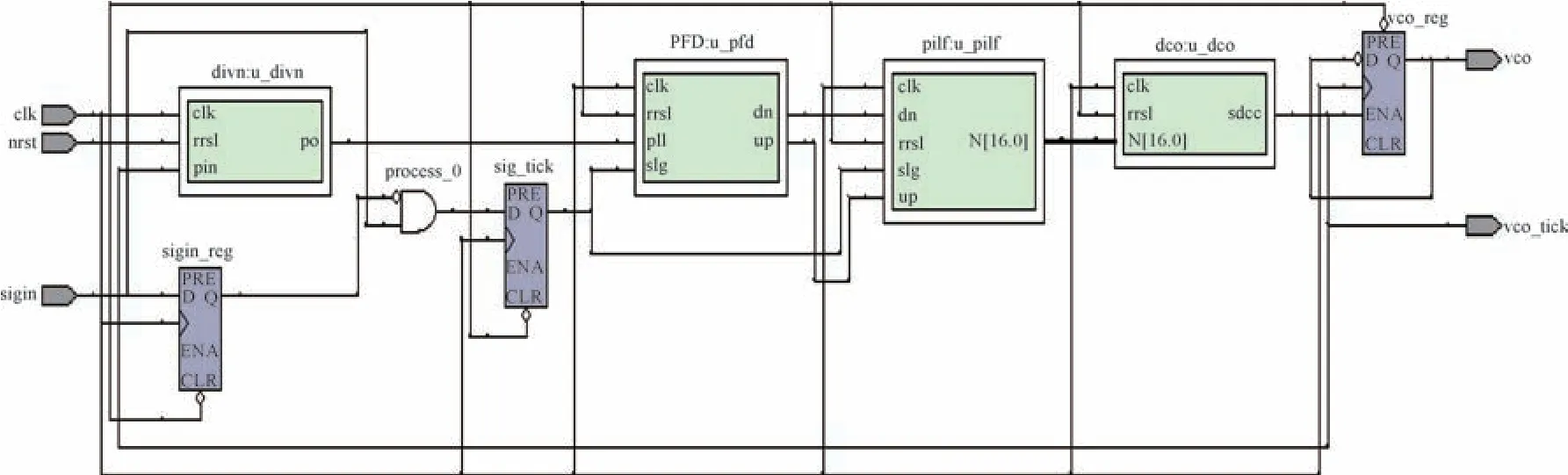
图2 锁相环RTL 实现框图Fig.2 Implementation block diagram of PLL RTL

基于Quartus II 软件对转子位置估计器进行了功能仿真, 结果如图3 所示。 从仿真结果可以看出, 锁相环可以对输入的过零脉冲信号进行频率倍频和相位锁定, 利用计数器对倍频信号进行计数便得到了转子位置。 图3 中, clk 为系统时钟信号, nrst 为上电复位信号, ph 为过零脉冲信号,position 为估计转子位置。

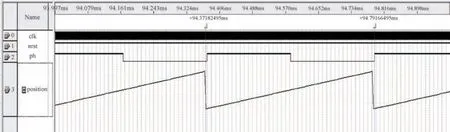
图3 锁相环转子位置估计器仿真图Fig.3 Simulation diagram of PLL rotor position estimator

2 正弦波驱动

理想情况下, 永磁同步电机的空载气隙磁密波形为正弦波, 也即转子磁动势为正弦波。 从电机工作原理上讲, 电磁转矩是转子磁动势和定子磁动势相互作用产生的, 所以仅当定子磁动势也为正弦波时, 永磁同步电机产生的电磁转矩才为恒定值。 对于已给定的电机, 定子本体参数是常数, 为了产生正弦波定子磁动势, 需要定子电流是正弦波, 这时定子绕组电流可表达为

式（1）中,I为定子绕组电流幅值,ωe为电机电气角速度,θ为转子磁场与定子电流之间的相位差。

陀螺永磁同步电机转子大都采用无铁芯设计,在定子电流为正弦波时, 其电磁转矩计算公式可表示为［10］

式（2） 中,P为转子极对数,λaf为转子永磁磁链。

从式（2）可以看出, 定子绕组电流为理想的正弦波时, 永磁同步电机输出的电磁转矩将为恒定值, 转矩波动最小, 这有利于电机实现转速的高稳定性控制。 因此, 本文采用了永磁同步电机正弦波线性驱动方案, 方案具体实现如下: 首先基于转子位置估计器获取的转子位置在FPGA 内部通过查表产生正弦给定电流, 然后利用外部D/A 转换器产生理想的正弦波电流去驱动陀螺动压气浮永磁同步电机。

3 电机控制系统设计

本文设计了速度环和电流环组成的双闭环控制系统, 来提高系统抗扰动性能, 增强转速波动抑制能力, 从而保证高速动压气浮永磁同步电机的转速控制精度, 控制系统组成如图4 所示。

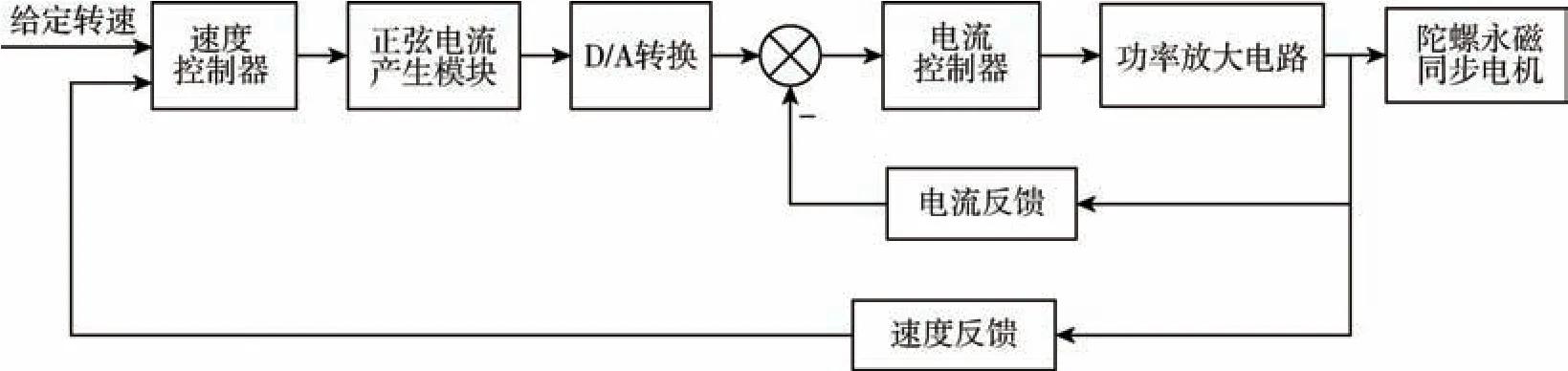
图4 电机控制系统组成框图Fig.4 Block diagram of motor control system

动压气浮永磁电机控制采用id=0 矢量控制方式, 其在dq旋转坐标系下的磁链方程、转矩方程和电压方程可描述为

式（3） ～式（5）中,ψd为d轴磁链,ψq为q轴磁链,ψr为转子磁链,Lsq为q轴电感,iq为q轴电流,ud为d轴电压,uq为q轴电压,Rs为定子电阻。

对于定子无铁芯、转子表贴式动压气浮永磁同步电机, 忽略直轴电枢反应影响, 其电压方程可描述为

式（6） 中,E=ωeψr为反电势,为电气时间常数。

对式（6）进行Laplace 变换, 经整理可得

动压气浮永磁同步电机的机械运动方程可写为

式（8）中,J为动压气浮电机的转动惯量,B为风阻摩擦系数。

将电磁转矩方程带入机械运动方程, 经整理可得

式（9）中,Kt=Pψr为电机转矩系数。

对式（9）进行Laplace 变换, 经整理可得

在多闭环控制系统设计时, 先设计内环, 再设计外环。 设计外环-速度环时, 可把内环-电流环看作速度环的一个调节对象。

3.1 电流环设计

永磁同步电机正弦波驱动的电流环主要由电流反馈回路、电流控制器和功率放大环节组成。电流反馈回路采用差分运算放大电路对电机相电流进行采集, 同时增加了电容滤波来消除电磁干扰。 因此, 电流反馈回路可等效为一阶惯性环节,传递函数可写为

式（11）中,Kc为线性放大系数,To为滤波延迟时间。

功率放大环节采用推挽电路来实现, 作用是对电流控制器的输出信号进行线性放大, 因此它可看作一个比例环节, 传递函数可表示为

式（12）中,Ko为比例放大倍数。

综合各环节的模型函数, 建立的电流环等效结构图如图5 所示。 图5 中,Gc（s）为电流控制器函数。

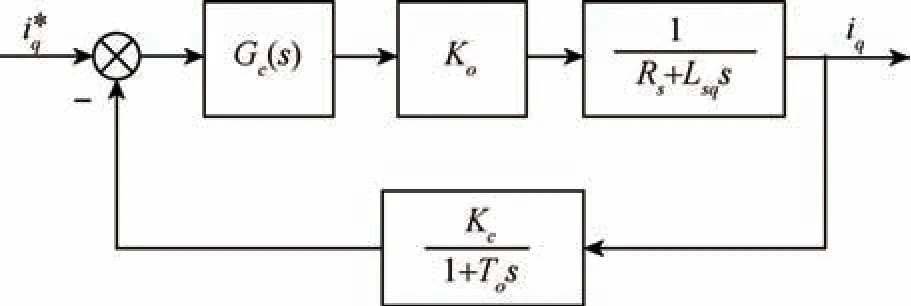
图5 电流环等效结构图Fig.5 Equivalent structure diagram of current loop

根据电流环等效结构图, 其开环传递函数可描述为

电流环作为电机双闭环控制系统的内环, 在系统动态响应上应保证快速跟随, 在稳态控制上应实现系统无静差, 因此电流调节器采用比例-积分控制。 为了保证电流控制的实时性, 本文采用运算放大器来构建PI 调节器, 其传递函数可表示为

式（14） 中,Kp为比例系数,τc为积分时间常数。

3.2 速度环设计

速度环的作用是消除负载转矩扰动, 保证电机实际转速精确跟踪给定转速。 本文设计中, 速度环的组成主要包括速度控制器、电流环、永磁同步电机本体和速度采集环节等。 考虑到速度环的带宽远低于电流环, 因此本文将电流环等效为一个比例环节, 其传递函数可表示为

对于永磁同步电机本体, 其机电时间常数与电气时间常数相比一般大很多, 所以其数学模型可近似为一阶惯性环节。 综上, 速度环的调节对象可看作是一个比例环节和一阶惯性环节的串联。

速度采集通过计算电机机械频率信号的周期来得到, 其中时钟基准由系统晶振提供, 这在一定程度上对瞬时转速进行了滤波平均, 所以速度反馈环节可以看作一阶惯性环节。

根据各环节的等效模型, 建立的速度环等效结构图如图6 所示。 图6 中,Kda为D/A 电路的转换系数, 为常数。

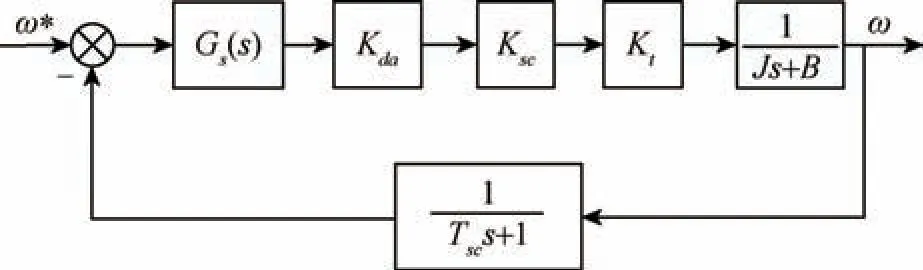
图6 速度环等效结构图Fig.6 Equivalent structure diagram of speed loop

由图6 可得速度环的开环传递函数为

为了实现速度控制无静差, 同时具有较强的抗干扰能力, 本文设计的速度控制器采用比例-积分调节, 其传递函数可表示为

式（17）中,Kn为控制器增益,τn为控制器积分时间常数。

利用Matlab 软件对搭建的动压气浮永磁同步电机双闭环控制系统进行了仿真, 仿真参数如表1所示。 工作转速为25000r/min, 在给定速度阶跃后得到的速度响应曲线如图7 所示。 由图7 可知, 速度上升时间很短, 系统具有很快的响应速度, 因此可保证电机控制系统具有良好的动态性能。

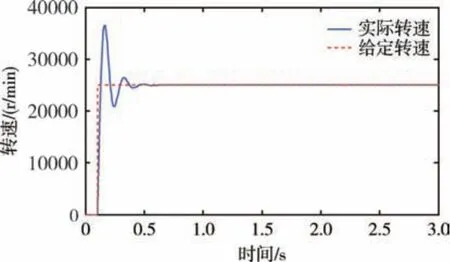
图7 速度阶跃响应仿真图Fig.7 Simulation diagram of speed step response

4 试验结果

利用正弦波驱动电路连接动压气浮永磁同步电机进行了试验。 在25000r/min 下, 锁相环可以很好地对反电势过零脉冲信号进行倍频, 然后利用计数器对倍频信号进行计数便得到了转子位置。基于获得的转子位置, 通过查找正弦表产生了理想的正弦波给定电流去驱动陀螺永磁同步电机,如图8 所示。 因此, 电机可以产生平稳的电磁转矩, 使得动压气浮永磁同步电机具有较高的转速稳定性。 另外, 在定子驱动电流为正弦波时, 由于电机空载反电势为正弦波, 且电机电感很小近似可以忽略, 所以电机相电压波形也近似理想正弦波。

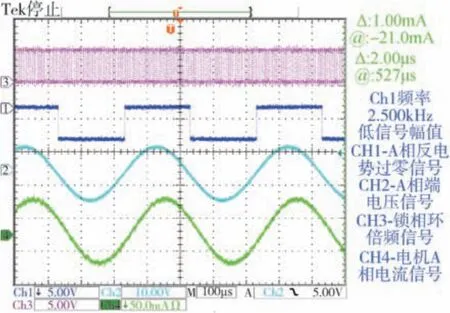
图8 锁相环转子位置估计测试Fig.8 Estimation test of PLL rotor position

采用正弦波线性驱动时, 测试得到的动压气浮永磁同步电机转速曲线如图9、图10 所示, 电机参数如表2 所示。 由图9 可知, 不同转速下电机均可稳定运行, 本文提出的控制方法可以适应电机较宽的工作转速。 对于陀螺动压气浮电机来说,工作转速一般是恒定的, 在额定转速25000r/min下, 稳定工作时标准差为0.380r/min, 转速稳定性达到了1.52 ×10-5, 这有利于保证陀螺仪输出的高精度。

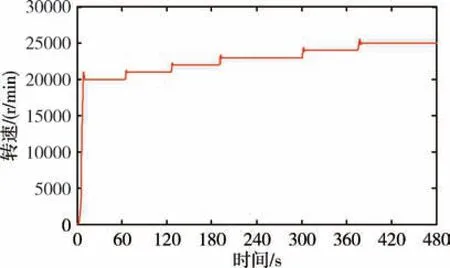
图9 电机不同转速曲线Fig.9 Curve of different motor speeds

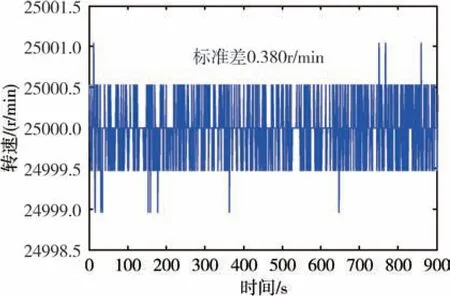
图10 稳定状态下的电机转速曲线Fig.10 Motor speed curve under steady-state

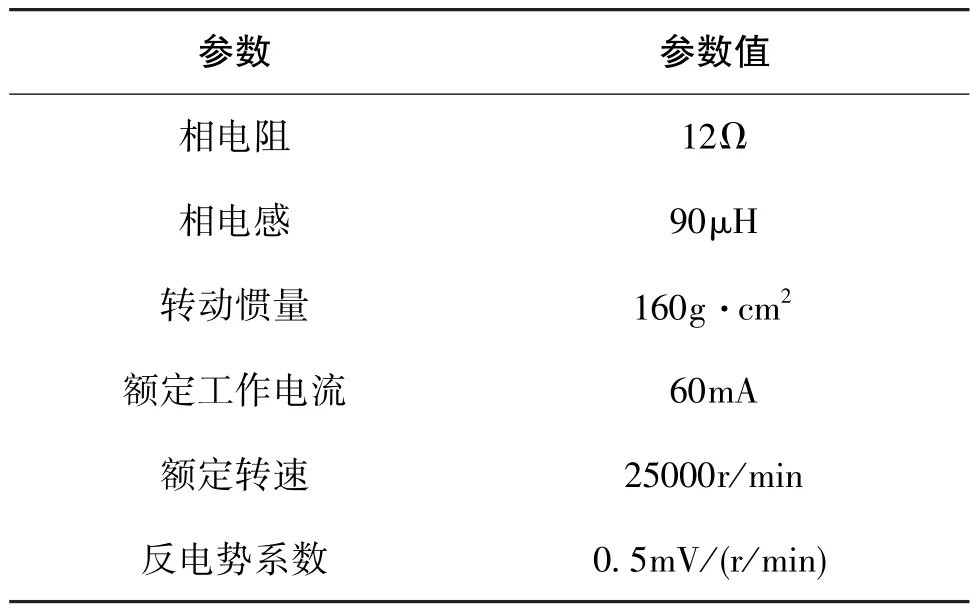
表2 电机参数Table 2 Motor parameters

同时, 基于反力矩系统测试了动压气浮永磁同步电机稳定运行时力矩的变化情况, 反力矩系统组成如图11 所示, 测试得到的力矩曲线如图12所示。 由图12 可知, 电机稳定运行时的力矩波动与反力矩测试仪自身零位波动相当, 所以采用正弦波驱动时电机输出的转矩是比较平稳的, 因此可以保证陀螺电机高转速稳定性。

5 结论

本文针对动压气浮高速永磁同步电机无位置传感器控制, 基于锁相环设计了一种转子位置估计器, 获得了转子位置; 采用了正弦波线性驱动,降低了电机转矩波动; 构建了电机双闭环控制系统, 提高了转速波动抑制能力。 仿真和试验表明,锁相环可以精确对反电势过零脉冲信号进行倍频来获取转子位置, 然后基于转子位置信息通过D/A 转换器产生理想的正弦波电流去驱动动压气浮永磁同步电机, 电机转速稳定性达到了1.52 ×10-5, 因而可保证陀螺仪测量的高精度。