基于信号源优化选择的集群飞行器协同定位方法研究

何 辉, 王 融, 熊 智, 刘建业, 刘瑶凯

（南京航空航天大学自动化学院导航研究中心, 南京 211106）

0 引言

现代战争以信息化为主要特征, 一体化程度不断提高。 为了提高整体作战效能, 实现资源优化配置, 作战飞机会成群出动组成机群网络共同执行任务, 机群组网将成为空中行动的一种工作模式［1］。 机群的精确定位技术是机群组网、协同空战的关键技术, 得到精确的导航定位信息是完成飞行器集群任务的必要条件之一, 一定精度以上的导航信息也是实现编队控制的基础。 实现协同作战的关键在于机群之间共享导航数据, 使机群里的任一成员都能将各自传感器检测到的信息实时共享［2］。因此, 如何根据收集到的数据高效合理地选取信号源信息是实现高精度协同导航定位的关键。

近年来, 多篇论文反映了国外在协同导航信号源方面进行的深入研究: 文献［3］ 研究了GPS/INS 三种不同组合情形下的相对导航; 文献［4］研究了GPS/INS 相对导航, 将长机的GPS 和INS 量测信息发送于僚机, 在僚机上采用容错联邦滤波器用相对GPS 量测信息估计相对INS 误差; 文献［5］基于编队成员相互测距信息优化惯导位置精度实现了机群组网定位; 文献［6］提出了利用RBF辅助的导航算法修正相对导航的精度; 文献［7］研究了基于GDOP 的JTIDS 相对导航定位源选择, 分析了JTIDS 相对导航性能及误差源; 文献［8］建立了混合概率模型, 降低了积分误差, 利用视觉与INS 的IMU 数据进行自主相对导航。

本文的集群编队系统采用了对等式结构, 相较于集中式和分布式结构, 对等式结构具有无源定位和高精度相对导航的能力［9］, 能够实时截获和锁定节点相对坐标, 间接校正飞行器节点导航系统的数据, 并传递分享自身导航源数据。 基于机载数据链, 结合INS 和GPS 数据, 引入高精度的测距测角信息, 研究飞行器的位置误差分布和信号源选择对协同导航定位精度的影响, 优化协同定位信号源选择, 提高集群系统的导航定位精度。

1 集群飞行器协同导航定位架构

每架飞行器均配备了导航定位设备、相对测距传感器、测角传感器、气压高度计、板载计算机等。 其中, 待定位飞行器自身定位精度低, 而基准飞行器定位精度较高。 如图1 所示, 整个集群系统通过数据链路进行通信, 在飞行过程中各机获得的导航信息均可通过数据链进行共享, 待定位飞行器可以获取基准飞行器的位置坐标信息和相对方位角、高度角信息以及相对测距信息, 系统的专有链路可以保障集群节点间共享的大信息量与高更新速率。

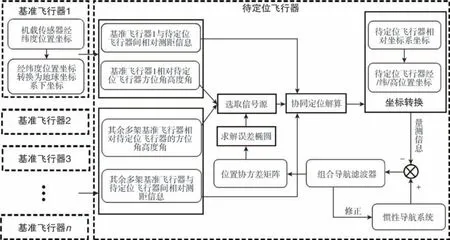
图1 协同导航定位架构图Fig.1 Diagram of collaborative navigation and positioning architecture

通过待定位飞行器导航系统中组合导航Kalman 滤波器得到反映待定位飞行器位置不确定度的位置协方差矩阵, 进一步求解得到待定位飞行器的位置误差椭球, 根据位置误差椭球的轴长及方向以及基准飞行器所处方位选取信号源, 结合待定位飞行器与信号源基准飞行器之间相对距离和信号源位置信息完成协同定位解算, 将得到的待定位飞行器位置信息进行坐标转换后作为量测信息对待定位飞行器的定位辅助修正, 以提高待定位飞行器的导航定位精度。

2 集群飞行器相对观测关系模型

2.1 协同定位原理

如图2 所示, 基准飞行器Aj的相对位置矢量坐标为（xj,yj）（j=1, 2）, 待定位飞行器B的相对位置矢量坐标为（x,y）, 两架基准飞行器对区域内的待定位飞行器进行观测, 所测得的相对距离分别为d1和d2, 以基准飞行器的位置为圆心, 相对距离为半径的两条圆弧的交点即为待定位飞行器的位置。

图2 协同导航定位示意图Fig.2 Schematic diagram of cooperative navigation and positioning

测量的过程中会存在误差, Δd1和Δd2分别为两架基准飞行器的距离测量误差, 并假设它们服从正态分布且相互独立。 测距误差对待定位飞行器位置估计的影响体现在位置线不再交于一点,虚线表示带有测量偏差的位置线。 因为测距误差是随机的, 所以四条虚线围成位置不确定域表示待定位飞行器的位置误差椭圆（灰色阴影部分）。

2.2 位置误差椭圆

导航系统误差等于导航系统计算位置与实际位置之差, 该误差包括系统误差和随机误差两部分。 其中, 系统误差为固定误差, 是稳定量, 可以通过测试得出; 对于随机误差, Kalman 滤波的协方差矩阵给出了导航系统的随机误差估计值,其中的经纬度误差可以用于位置不确定度的计算,得到如图3 所示的误差椭圆。

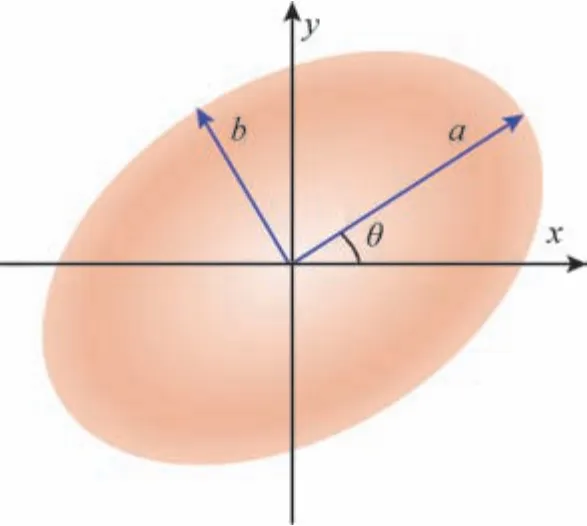
图3 误差椭圆示意图Fig.3 Schematic diagram of error ellipse

对于使用扩展Kalman 滤波的组合导航系统,其各项误差之间是相互独立的, 而且都是随机误差。 假定所有误差均服从Gauss 分布, 可以利用Kalman 滤波的协方差矩阵获得位置误差矩阵Epos和位置协方差矩阵Ppos

式（2）、式（3） 中,δL为纬度误差,δλ为经度误差,σ2为方差。

将导航系统的经纬度误差转化为平面内的直线误差

式（4）中,R为地球半径,L为待定位飞行器所在纬度。

由式（4）可将Epos和Ppos转换得到位置误差的协方差矩阵ppos

计算得到位置协方差矩阵ppos的特征值γ1和γ2, 用来确定待定位飞行器误差椭圆E的长半轴和短半轴［10］

式（7）中,a为长半轴,b为短半轴, 且误差椭圆长半轴与x轴成θ角

3 集群飞行器协同导航信号源选择分析

在集群飞行过程中, 定位精度高的飞行器作为信号源基准飞行器, 自身定位精度较差的飞行器被设定为待定位飞行器, 通过数据链路得到周围基准飞行器的导航信息。 根据相对几何关系选择信号源, 选取误差椭球长轴方向的信号源辅助定位, 可有效减小待定位飞行器定位误差［9］, 从而提高协同导航定位精度。

首先, 需将各飞行器机载导航传感器的经度、纬度和高度坐标转换为地球坐标系坐标（Earth-Centered, Earth Fixed, ECEF）, 转换公式如下

式（9）中,RN为地球卯酉圈曲率半径,f为地球扁率,λj为飞行器j的经度,Lj为飞行器j的纬度,Hj为飞行器j的高度,为转换的各飞行器地球坐标系坐标。

进一步建立以待定位飞行器为坐标原点的相对坐标系, 计算待定位飞行器至各基准飞行器间的相对角度信息, 并得到相对高度角αj、相对方位角βj和飞行器相对坐标关系方程

式（10）中,αj为待定位飞行器至各基准飞行器间的相对高度角信息,βj为待定位飞行器至各基准飞行器间的相对方位角信息, （x,y,z） 为待定位飞行器在相对坐标系下的位置坐标,为基准飞行器在相对坐标系下的位置坐标。

如图4 所示, 点O为待定位飞行器的原点位置,E为待定位飞行器的位置误差椭球,A为基准飞行器,a为误差椭球长轴, 具体迭代选择流程如图5 所示。

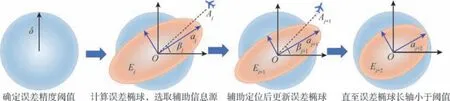
图4 椭球迭代示意图Fig.4 Schematic diagram of ellipsoid iteration

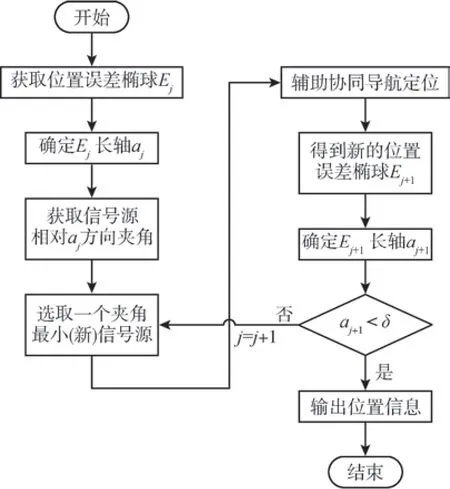
图5 迭代算法流程图Fig.5 Flowchart of iterative algorithm

算法的流程步骤为:

1）设定初始半径为δ的球体作为误差精度的阈值, 由Kalman 滤波器的位置协方差矩阵求得待定位飞行器当前时刻的位置误差椭球Ej;

2）计算误差椭球Ej的轴长大小, 根据椭球Ej长轴aj所在方向, 选取与长轴方向最近的信号源基准飞行器Aj;

3）利用选取的Aj信息对待定位飞行器进行辅助定位, 再根据更新后的协方差矩阵得到新的误差椭球Ej+1;

4）判断Ej+1长轴aj+1大小是否已小于预设的阈值δ, 若aj+1＞δ, 则根据新的长轴aj+1选取其所在方向最近的信号源基准飞行器Aj+1, 再次进行辅助定位后得到新的误差椭球Ej+2及长轴aj+2;

5）继续比较aj+2和δ的大小, 重复迭代至aj+n＜δ, 停止继续选取信号源, 并输出辅助定位后的位置信息。

4 仿真与分析

4.1 仿真条件设置

本次仿真设置参与集群的飞行器数量为11 架,其中的10 架高精度飞行器作为基准飞行器, 1 架定位精度较低的飞行器作为待定位飞行器。 图6 为仿真设置的11 架集群飞行器飞行航迹, 各飞行器仿真参数如表1 所示。

图6 集群飞行器轨迹Fig.6 Trajectories of cluster aircrafts

表1 集群飞行系统仿真参数Table 1 Simulation parameters of cluster flight system

图6 中, 虚线为待定位飞行器, 其余实线（编号1 ～10）为基准飞行器。 在飞行过程中, 待定位飞行器根据定位误差椭球选取合适的基准飞行器作为信号源辅助定位, 仿真记录飞行过程中误差椭球的变化以及所选取的信号源基准飞行器编号,并对信号源优选的协同定位结果进行分析。

4.2 结果分析

如图7 所示, 选取第300s 的待定位飞行器定位误差进行分析。 图7（a）为待定位飞行器初始的误差椭球, 根据误差椭球长轴所在方向选取基准飞行器作为信号源辅助定位, 得到修正后的误差椭球如图7（b） 所示。 对比可知, 误差椭球的各轴长变小, 表示待定位飞行器的定位误差经过信号源辅助修正后减小。 图8 选取了某一时刻飞行器位置分布情况, 并用星形（★）标注了被选取的辅助定位信号源基准飞行器编号。

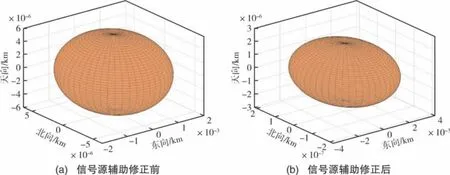
图7 第300s 待定位飞行器位置误差椭球Fig.7 Position error ellipsoid of the aircraft to be positioned in the 300th second

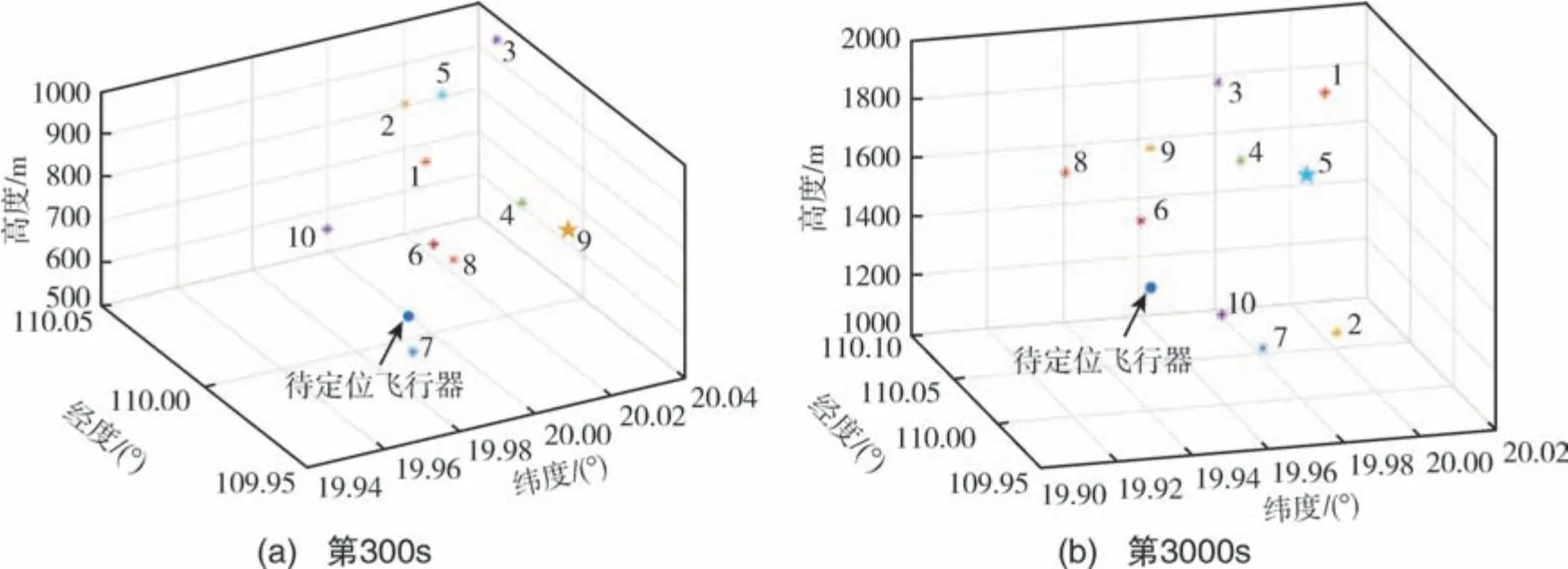
图8 飞行器位置分布及信号源Fig.8 Schematic diagram of aircraft position distribution and signal sources

由图9 可知, 在选取信号源基准飞行器辅助定位过程中, 按照优选顺序使用所有信号源辅助定位, 随着信号源迭代次数增加, 椭球的轴长有递减的趋势, 在迭代4 ～5 次后, 椭球轴长已趋近于阈值, 表明后续选取信号源对定位精度提升的作用较小。 图10 显示了飞行仿真过程中被优化选取的信号源飞行器编号变化情况。 在实际飞行中,飞行器的高度数据一般由气压高度计给出, 在仿真结果中主要分析经纬度误差, 将经纬度误差综合转换为“米”, 分别计算选取所有信号源辅助定位和随机选取信号源辅助定位, 通过待定位飞行器的位置误差累积分布概率与本文采用方法对比。由图11 可知, 采用本文信号源迭代优化选择方法可较快地提高协同定位精度, 且定位精度和效率优于随机选取信号源辅助定位的结果。

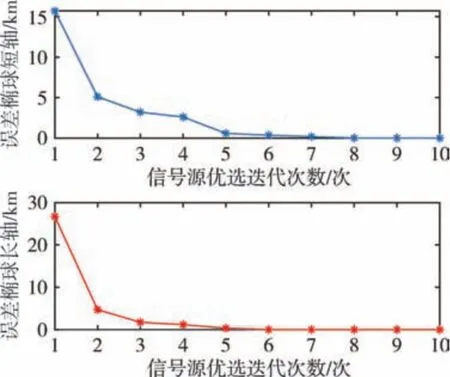
图9 误差椭球轴长变化情况Fig.9 Axial length changes in error ellipsoid

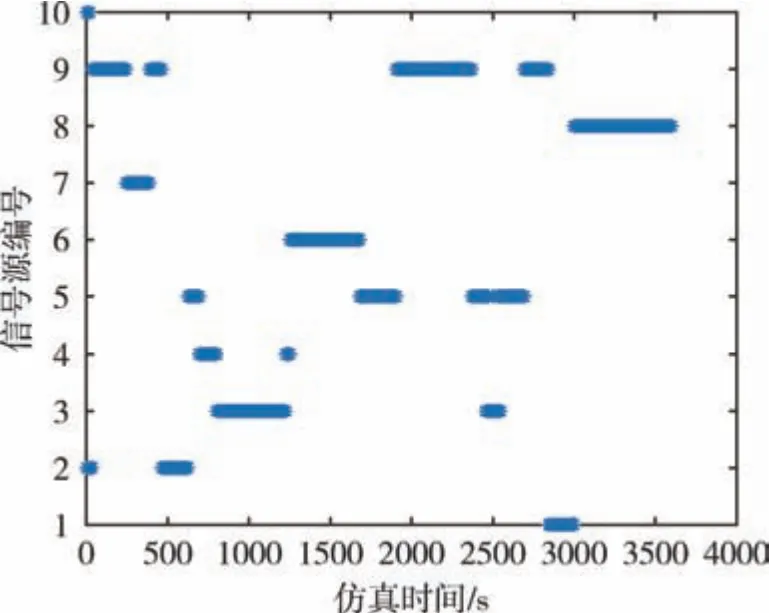
图10 信号源优选编号变化情况Fig.10 Number changes in signal source optimal selection

图11 定位结果位置误差对比Fig.11 Position error comparison of positioning results

5 结论

针对集群飞行器协同导航定位问题, 本文提出了一种基于飞行器位置误差椭圆的信号源选择协同导航算法, 通过位置误差椭球迭代的方式选取信号源进行辅助定位, 对低精度飞行器的机载导航信息进行修正, 最后从飞行器误差椭球轴长的变化、飞行器位置误差的累积分布概率等方面进行了对比仿真验证。 仿真结果表明, 椭球迭代信号源选择算法可以有效提升待定位飞行器的定位精度, 增强集群协同导航定位效率。