高过载惯导误差建模与补偿方法

白钲皓, 张 琨, 王国栋, 程 玉, 陈 帅

（1. 南京理工大学, 南京 210094; 2. 北京航天控制仪器研究所, 北京 100039）

0 引言

因自主性强、尺寸小、成本低等特点, 微惯性测量单元（Miniature Inertial Measurement Unit,MIMU）被广泛应用于现代军事领域。 在弹载冲击环境下, 惯性器件会受到非常严重的影响, 过载前后的性能（零偏、标度因数等） 很难保持一致［1］,由此产生的误差在惯性导航解算中会迅速积累。因此, 研究过载冲击对惯性器件的影响十分必要。现有的标定模型大多工作在低动态、低过载环境下［2］, 有学者在此基础上建立了导弹过载段的多源误差模型［3］, 主要针对过载段的系统误差模型进行分析。

惯性导航系统的误差与初始参数和器件误差的标定精度直接相关, 需对器件误差进行标定以保证惯性导航系统的定位精度［4］。 区别于传统标定方法, 借助于武器平台的高精度主惯导系统提供的信息, 利用传递对准可实现精确的初始对准和子惯导系统误差的估计与补偿［5］。 传递对准常用的匹配方式有速度匹配、速度+姿态匹配等, 在引入姿态作为观测量后可以极大缩短对准时间［6］。 由于GPS 信号易受到干扰, 不能完全依赖GPS 进行组合导航, 有学者针对此问题提出了速度约束和高程约束两种方法, 提高无卫星导航情况下的导航系统能力［7］。 非完整性约束利用载体的侧向和天向速度为零的约束条件对惯导导航误差进行修正,可实现无外部传感器条件下的自主导航［8］。 目前,纯惯性导航的研究都采用较高精度的惯导和自对准的方式进行验证, 存在惯导成本高昂、自对准精度低且机动性差等问题。 因此, 针对低精度惯导, 有必要研究一种动基座精确对准的方法以提高惯导的纯惯性导航定位精度。

本文分析了过载冲击对惯性器件的影响, 建立了冲击误差补偿模型以实现对惯性器件误差的补偿。 提出了一种传递对准与运动约束辅助的导航定位方法, 针对该方法的两种算法建立了统一的系统模型和不同的观测模型。 通过半实物仿真验证该方法的可行性, 实现了惯性传感器误差的标定与校正, 提高了无卫星导航情况下的自主导航定位精度。

1 过载冲击下的MIMU 误差建模

1.1 MIMU 误差分析

目前, 惯性器件一般采用刚体外框架和灌胶封装实现抗高过载, 当惯导受到过载冲击时可以保证其完好, 但不可避免地会发生性能参数（如零偏、标度因数、稳定性等）变化［9］, 导致惯导的零偏与标度因数相较于冲击前会产生一定变化, 而静态标定模型未对其进行修正, 造成测量结果的误差。

陀螺仪的输入输出模型为

式（1）中,F为陀螺仪的输出,Kg为陀螺仪的标度因数,Ωr为陀螺仪的输入,Kg0为陀螺仪的零偏,v为拟合误差。 假设此时标度因数和零偏因陀螺仪受到冲击而存在误差, 则冲击后的陀螺仪测得的输出为

式（2）中,Fc为陀螺仪冲击后的输出,δKg为冲击引起陀螺仪的标度因数变化量,δKg0为冲击后陀螺仪的零偏变化量,vc为拟合误差。 根据式（1）所示的陀螺仪输出模型计算角速度, 并将式（2）带入式（1）得到陀螺仪的角速度

式（3）中,v1为拟合误差。 令, 可得陀螺仪受到冲击后的输出误差模型

式（4）中,δΩc为陀螺仪角速度误差,δg0为陀螺仪冲击后的拟合零位变化量。

同理, 加速度计受到冲击后的输出误差模型为

式（5）中,δfc为加速度计比力误差,Kf为加速度计的标度因数,f为加速度计输入,δKf、δf0分别为冲击引起加速度计的标度因数与拟合零位的变化量,v2为拟合误差。 由式（4）和式（5）可知, 当载体受到高过载冲击时, 标度因数会增大比力和角速度误差, 使定位精度快速发散。

1.2 MIMU 误差补偿模型

考虑到MIMU 的零偏误差、标度因数误差与安装误差, 根据器件物理特性建立陀螺仪与加速度计的误差模型［10］。 根据式（4）和式（5）, MIMU 受到过载冲击后, 标度因数与零偏会发生变化, 使已有的误差模型不再完全适用。 对惯性器件沿x轴方向进行过载冲击, 对MIMU 的x轴在不同冲击下产生的冲击误差进行建模分析, 惯性器件沿冲击方向的轴向（x轴）受冲击作用影响明显。 利用标定模型计算每次冲击后的各项参数, 利用基于最小二乘法的多项式回归模型拟合参数的变化, 多项式如下

式（6）中,s为MIMU 受到的冲击量级,ai（i=1, 2, …,n）为多项式系数。 在原有的标定模型上, 利用拟合的变化曲线代替原有模型中的部分常值, 构建基于冲击量级的动态补偿模型, 其补偿原理如图1 所示。

图1 惯性传感器冲击补偿模型Fig.1 Shock compensation model of inertial sensor

根据上述补偿原理可得新的MIMU 陀螺仪和加速度计的误差模型, 此处以陀螺仪为例

式（7） 中,W= ［WxWyWz］T为MIMU 陀螺仪的实际测量值,fωx（s）、fx（s）为陀螺仪x轴的零偏和标度因数为冲击量级的函数,ωy0、ωz0为其余两个轴的零偏,Kωi、Kωij（i=x,y,z;j=x,y,z）分别为陀螺仪的标度因数与安装误差系数,ω=［ωxωyωz］T为陀螺仪实际的角速度。

2 MIMU 在线误差补偿与约束

由于微惯性传感器会存在各种固有误差, 包括陀螺零偏、加速度计零偏、安装误差角等, 导致纯惯性导航定位误差随时间累积迅速发散。 传统的分立式标定方法需要对MIMU 进行转台实验,这既增加了设备成本, 也不利于现场标定的应用需求。 通常, 系统模型采用固定误差会存在较大的剩余误差, 需要对MIMU 进行实时修正。 考虑到系统无外部辅助信息的定位需求, 直接采用惯性导航算法无法有效地抑制系统累积误差。 针对上述问题, 采用一种传递对准与运动学约束辅助的方法, 既可以实现精确对准和实时误差修正, 又能提高无卫星导航情况下的纯惯性导航定位精度。

2.1 传递对准系统模型

传递对准分为粗对准和精对准两个阶段, 粗对准是将主惯导精确的初始姿态、位置、速度信息传递给子惯导, 精对准是利用Kalman 滤波在线估计子惯导的零偏误差, 同时对主子惯导杆臂和安装误差角进行实时估计［11］, 选取系统状态量为

式（8）中,φ为子惯导姿态误差,δvn为速度误差,εb为子惯导陀螺零偏,Δb为加速度计零偏,μb、lb分别为主子惯导安装角误差和杆臂误差。 本文使用基于地理系（东北天坐标系）的惯导系统误差模型, 结合捷联惯导误差方程可得系统方程［12］为

建立Kalman 滤波器状态方程

式（10） 中,Φ为状态转移矩阵,W为系统噪声矩阵。

根据文献［13］构建系统量测方程

式（11） 中,V1为量测噪声,H1为量测矩阵。H1满足

2.2 运动学约束

定义载体直角坐标系m系,y轴指向载体前进方向,x轴沿横轴指向右侧,z轴指向载体上方。载体运动学约束条件是指: 载体在运动过程中仅有前向动力, 不发生侧滑和跳跃, 则载体在x轴和z轴的速度分量为零, 即

载体运动速度可表示为

对式（14）进行全微分, 得到

由式（13）和式（16）可以构造运动学约束的量测方程

式（17） 中,V2为量测噪声,H2为量测矩阵。H2满足

3 实验与仿真分析

本次实验使用了MEA200 高过载惯导作为子惯导, 对上文提出的MIMU 冲击补偿模型和传递对准与运动学约束辅助进行验证: 首先, 对子惯导进行不同量级的冲击实验, 采集惯导数据建立冲击补偿模型; 再将高精度组合导航系统安装在实验车内, 用于模拟武器平台的导航系统, 为子惯导提供必要信息; 将子惯导与高精度导航系统安装在支架上并置于车厢内, 进行跑车实验并实时采集子惯导和组合导航系统数据, 利用冲击补偿模型修正子惯导的数据信息; 最后, 验证传递对准与运动学约束辅助方法的有效性。 MIMU 过载冲击实验如图2 所示, 跑车实验现场装车如图3 所示。

图2 过载冲击安装实验Fig.2 Diagram of overload shock installation experiment

图3 跑车实验现场装车图Fig.3 Diagram of the vehicle loading in the experiment equipment

3.1 冲击误差补偿实验

实验采用过载冲击设备对固定在落台上的高过载惯导撞击造成过载冲击, 冲击轴向为陀螺仪和加速度计的x轴。 实验对惯导依次进行了2000g～15000g的过载冲击, 该设备对惯导施加半正弦波的冲击, 冲击整体时间为0.5ms 左右, 每次冲击前后各采集3 组数据并对惯导进行性能测试与标定。

通过分析不同冲击量级的惯导数据, 惯性器件沿冲击方向的轴向（x轴） 受冲击作用影响明显,选取其一组数据对陀螺仪和加速度计x轴的零偏与标度因数进行多项式拟合。 综合考虑模型的计算量和准确性, 采用3 阶多项式模型对不同冲击量级造成的影响进行误差补偿。

为验证冲击误差补偿模型的效果, 以冲击后惯导的标定结果为基准, 选择另外一组数据比较惯导受过载冲击后的前1000 帧输出数据。 在10000g冲击下, 加速度计x轴冲击误差补偿曲线如图4 所示。 不同冲击量级下, 冲击误差补偿模型在x轴的补偿效果如表1 和表2 所示。 实验结果表明, MIMU 在受到10000g、15000g冲击情况下,相较于未补偿情况, 使用冲击误差模型补偿加速度计和陀螺仪, 其误差明显降低。

图4 加速度计x 轴冲击误差补偿曲线Fig.4 Diagram of accelerometer x-axis shock error compensation curves

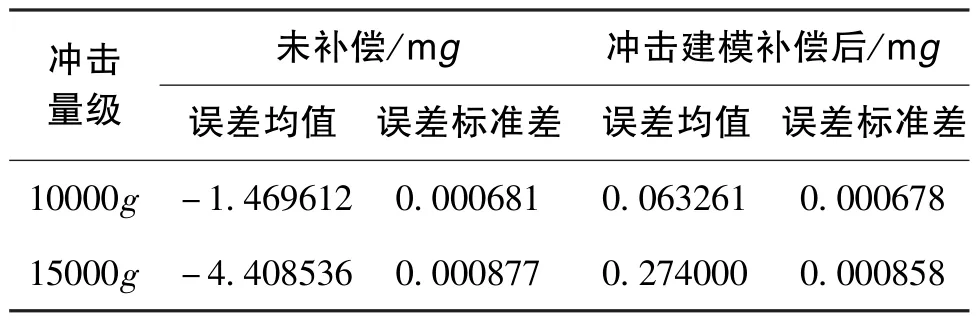
表1 加速度计x 轴冲击误差补偿对比Table 1 Comparison of accelerometer x-axis shock error compensation

3.2 跑车实验

跑车实验地点选在南京市麒麟公园空旷路段,行驶时间约为13min, 前6min 绕圈行驶进行主子惯导传递对准, 最后在500s 时行驶到指定位置, 停止传递对准, 子惯导切换为运动学约束导航行驶3min, 主惯导作为导航基准进行比较, 包含车辆直线行驶的所有状态, 跑车实验路线如图5 所示。

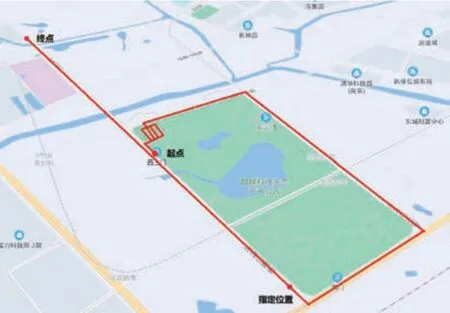
图5 跑车实验路线图Fig.5 Diagram of vehicle experiment route

实验采用MEA200 作为子惯导, 输出频率为50Hz, 陀螺仪三轴平均零偏稳定性实测优于11（°） /h,加速度计零偏稳定性为0.1mg。 主惯导采用KVH1750 高精度激光惯导, 陀螺仪零偏稳定性为0.05（°） /h。 选用NovAtel 公司的PwrPak7 接收机和KVH1750 惯导作为高精度组合导航系统, 其主要性能指标如表3 所示。 同时, 采集MIMU 和高精度基准数据, 离线进行导航算法验证。

表3 高精度组合导航系统主要性能指标Table 3 Main performance indexes of high-precision integrated navigation system

跑车实验行驶路径如图6 所示, 姿态误差曲线如图7 所示。 可以看出, 在行驶过程中主惯导姿态误差会影响子惯导误差估计。 在前6min 内绕圈行驶进行传递对准, 主惯导姿态存在波动, 因此子惯导姿态也存在较大波动, 姿态误差在0.8°以内;当传递对准完成后, 三个姿态角全部收敛, 姿态误差稳定在0.05°以内。 图8 为约束算法速度误差曲线, 速度误差在载体运动时存在波动, 主要是因为姿态不准确造成的。 从500s 开始停止传递对准, 之后进行运动学约束。 可以看出, 速度误差逐渐增大且存在一定幅度的波动, 原因是由于载体的前向通道没有约束。 图9 为纯惯性导航速度误差曲线, 前500s 与图8 一致, 存在小范围波动,之后停止传递对准开始纯惯性导航, 则速度误差相较于图8 明显发散。

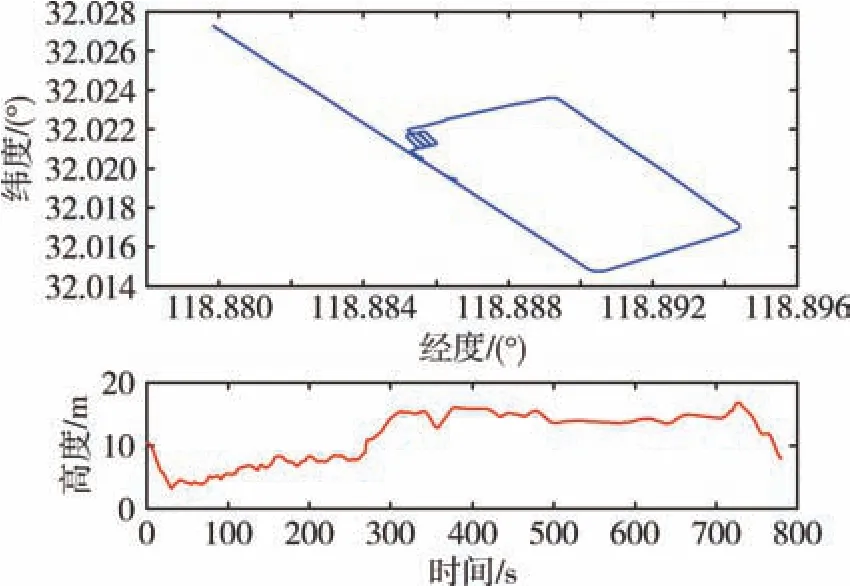
图6 跑车实验行驶路径Fig.6 Driving path of vehicle experiment

图7 姿态误差曲线Fig.7 Curves of attitude error

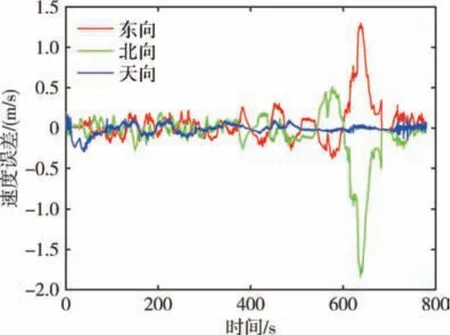
图8 约束算法速度误差曲线Fig.8 Speed error curves of constraint algorithm

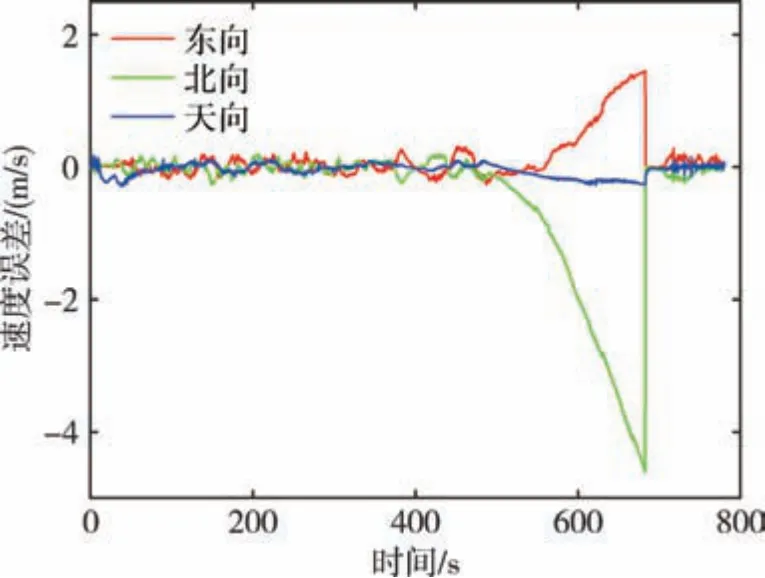
图9 纯惯性导航速度误差曲线Fig.9 Speed error curves of pure inertial navigation

图10 为运动学约束辅助下的惯性导航定位误差, 单向位置误差小于50m, 由于直线行驶期间偏航角未发生改变, 前向通道无法约束造成某个方向位置误差呈现一定累计趋势。 图11 给出了纯惯性导航定位误差, 可以看到位置误差快速积累, 单向位置误差在350m 以内, 由于主惯导通过传递对准为子惯导提供了相对准确的初始姿态, 也使得纯惯性导航定位精度得到一定程度的优化。 比较图10 和图11可知, 采用运动学约束辅助后, 导航定位精度提升了85%, 高度通道的发散趋势明显得到抑制。

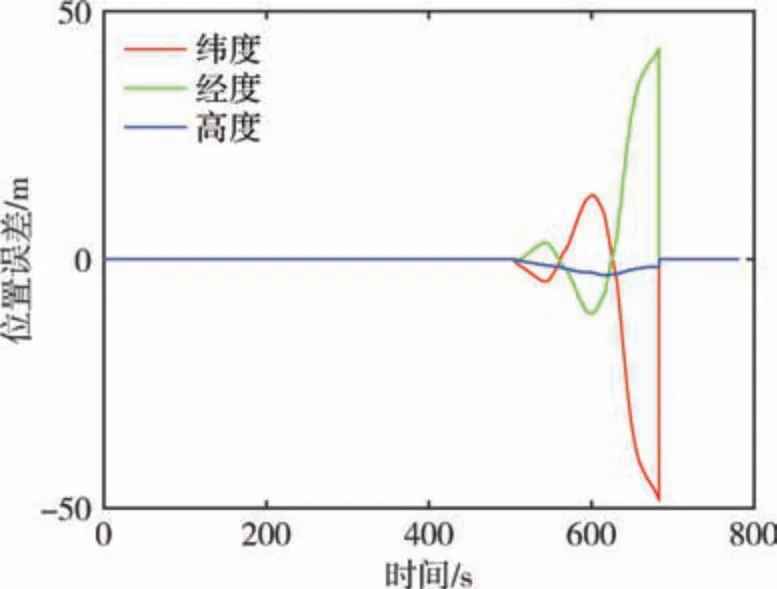
图10 约束辅助下的惯性导航定位误差Fig.10 Diagram of inertial navigation positioning error assisted by constraints

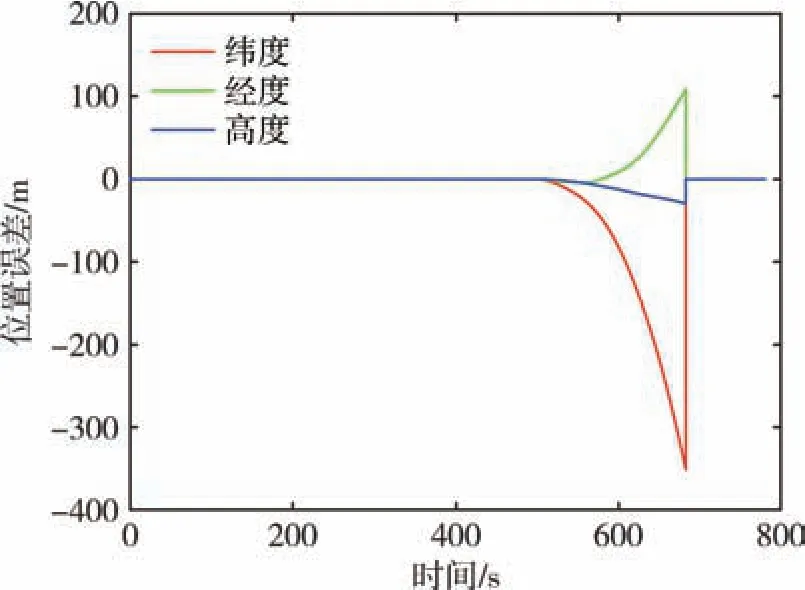
图11 纯惯性导航定位误差Fig.11 Diagram of pure inertial navigation positioning error

4 结论

针对高过载惯导受到冲击后零偏与标度因数产生一定变化的问题, 本文构建了基于冲击量级的动态补偿模型, 利用拟合参数动态调整MIMU 的误差模型, 从而减小了加速度计和陀螺仪的误差。同时, 本文研究了一种传递对准与运动学约束辅助的方法, 可对MIMU 进行误差在线标定与约束。仿真结果表明, 该方法可有效提高系统对准精度,实时修正系统误差, 可提高无卫星导航情况下的自主导航定位精度。