无人机视觉地理定位研究综述

朱得糠, 李东泽, 郭鸿博, 李 彤

（军事科学院国防科技创新研究院, 北京 100071）

0 引言

无人机具备低成本、高精度以及便捷飞行等优点, 近年来发展迅速, 特别是搭载光电载荷（可见光/红外相机） 的无人机, 被广泛应用于航空摄影测量与遥感［1-2］任务中, 为地理信息系统（Geographic Information System, GIS） 提供 基础 数据［3］,如绘制地形图。 无人机对地视觉定位任务模式不同于GIS 应用, 但其主要视觉处理原理与航空摄影测量一致, 属于航空摄影测量的一个分支, 该技术在军事领域的研究和应用由来已久［4］, 为侦察和引导打击提供情报支持。 随着无人机在民用领域的普及, 其应用也日益广泛, 如抢险救灾人员搜救、警用巡逻、森林植保防范火情等。

机载相机遵循小孔成像原理, 将三维空间目标投影到二维图像的过程中丢失了一个维度（深度）信息, 单个观测图像仅提供了目标的方向角度测量, 据此无法定位目标。 目前主要通过以下两种类型的方法解决上述问题: 一是补充额外信息的方法, 引入补充信息解算深度值从而确定目标位置; 二是统计估计方法, 从多角度观测的方向测量值中利用优化或滤波等方法估计目标位置。 补充额外信息方法的核心是利用相机的内外参数进行齐次坐标转换, 通过相机标定获得内参数, 从相应传感器读取外参数, 如从全球导航卫星系统（Global Navigation Satellite System, GNSS）读取无人机位置, 从航姿参考系统（Attitude and Heading Reference System, AHRS）读取无人机偏航/俯仰/滚转角等。 统计估计方法基于回归和优化对静止目标进行三角定位; 基于滤波估计定位运动目标, 原理上与纯角度跟踪（Bearing Only Tracking, BOT）一致。 虽然补充额外信息的许多算法也利用多次测量和统计方法提高定位精度, 但它们不是纯角度测量值的位置估计问题, 本文仍然把它们归为前者。

目前, 成熟的对地视觉定位手段是: 观察员从无人机回传的视频图像上人工识别并框选目标位置, 图像处理算法锁定或跟踪目标, 提供目标的图像位置测量值给定位算法。 识别框选目标主要由人工操作, 通常一次定位单个目标已经难以满足军事和民用需求, 特别是军用方面, 智能化战争时代正在加速到来, 战场的动态性和复杂性日益加强, 对多目标的快速识别和定位能力提出了迫切需求。

深度学习引领的人工智能高潮首先在计算机视觉领域取得了巨大突破, 目标检测识别性能在某些方面已经达到甚至超过了人类的水平, 出现了一批高效实用的算法, 如Faster RCNN［5］系列、YOLO［6］系列等。 算法引入航空遥感图像处理领域,能够替代观察员快速准确地在图像上识别框选多个目标。 目标检测能力的提升也提高了多目标跟踪性能, 典型的算法如DeepSort［7］与YOLO 算法相结合, 成为工程应用中的流行算法。 以上智能算法作用在图像域, 与无人机控制技术相结合提升无人机系统在空间域的智能化程度, 如自动跟踪飞行、自主打击引导等, 都需要以空间域目标定位技术为中介。 因此, 结合最新的人工智能计算机视觉技术拓展对地定位能力, 是无人机系统智能化升级的重要途径。

在军事领域, 无人机蜂群作战是近年的一个热门研究方向。 大量低成本无人机组成蜂群协同作战, 可以代替单个多功能无人机执行侦察监视、区域拒止等任务。 蜂群无人机协同目标探测, 具备感知范围大、重访周期短、多角度同时观测等优势, 通过信息融合可获得更高的识别准确率和定位精度。 多机协同探测的一个重要研究内容就是数据关联, 尤其是多目标检测和跟踪任务, 目标视觉特征和空间位置信息相耦合, 不同来源的数据关联时既要考虑视觉特征的相似性又要考虑空间位置的远近程度。 此应用场景为对地视觉定位提供了新的研究内容。

鉴于以上所述视觉定位技术的新要求和新思路, 非常有必要及时梳理总结其关键技术和研究现状, 以加速无人机的智能化发展。 本文系统总结了该领域近二十年的研究工作, 首先详细描述了对地视觉定位过程中各种坐标系的定义和相互转换关系, 从数学原理上指明问题的关键所在;其次全面梳理了单架无人机对地视觉定位研究现状, 按技术手段分为基于辅助地理信息、基于某一维距离、三角定位和纯角度跟踪滤波等四类方式; 然后整理了多架无人机协同定位的研究现状;最后预测了无人机对地视觉定位的未来发展趋势。

1 对地视觉定位坐标关系

无人机对地视觉定位任务涉及多个坐标系,许多文献为了简化算法描述, 没有全部用到, 或者忽略安装位置偏差等, 简化了坐标之间的转换计算。 本文从工程实践的角度出发, 将定位任务定义在常见的大地坐标系下, 由机载光学相机图像域中的目标位置求解大地坐标, 基于此全面细致描述了全部涉及的坐标系, 并给出相互转换计算方法。

1.1 坐标系定义

无人机对地定位需要利用无人机的空间位姿,涉及坐标系较多, 包括世界大地坐标系（World Geodetic System 1984, WGS84）、机载参考系、机体系、相机系、云台系和图像系, 下面分别展开描述。

（1）世界大地坐标系

因GNSS 广泛采用WGS84 世界大地坐标系,故而使其成为无人机导航领域广泛采用的地心坐标系——即原点与地球质心重合、固定在地球上与地球一起旋转的坐标系。 WGS84 有空间直角坐标和大地坐标两种等价表示形式, 它采用十分近似于地球自然形状的参考椭球作为描述和推算地面点位置和相互关系的基准面。 两种形式的坐标定义如下:

1） 空间直角坐标系是一种地心地固坐标系（Earth-centered Earth-fixed, ECEF）, 也称为地球坐标系, 简记为e系。Z轴指向BIH（1984.0）定义的地极（CTP）方向,X轴指向BIH 定义的零度子午面和CTP 赤道的交点,Y轴垂直于XOZ平面构成右手坐标系, 记为Oe-XeYeZe, 如图1 所示［8］。

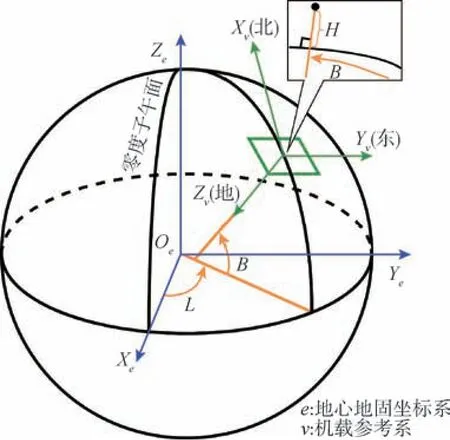
图1 WGS84 坐标系Fig.1 Schematic diagram of WGS84 coordinate system

2）大地坐标系是GNSS 定位数据采用的坐标系, 坐标（B,L,H）分别表示大地纬度B、经度L和高程H。 纬度是空间点与参考椭球面的法线与CTP 赤道面的夹角, 经度是空间点与参考椭球的自转轴所在的面与BIH 定义的零度子午面的夹角,大地高程是空间点沿着参考椭球的法线方向到参考椭球面的距离, 具体如图1 所示。

（2）机载参考系

以无人机质心为原点的北东地（North-East-Down, NED）坐标系依据WGS84 椭球模型定义,X轴指向北极（即正北方向）,Y轴指向正东方向,Z轴垂直于O-XY平面向下指向地面, 记为Ov-XvYvZv, 如图2（a）所示。

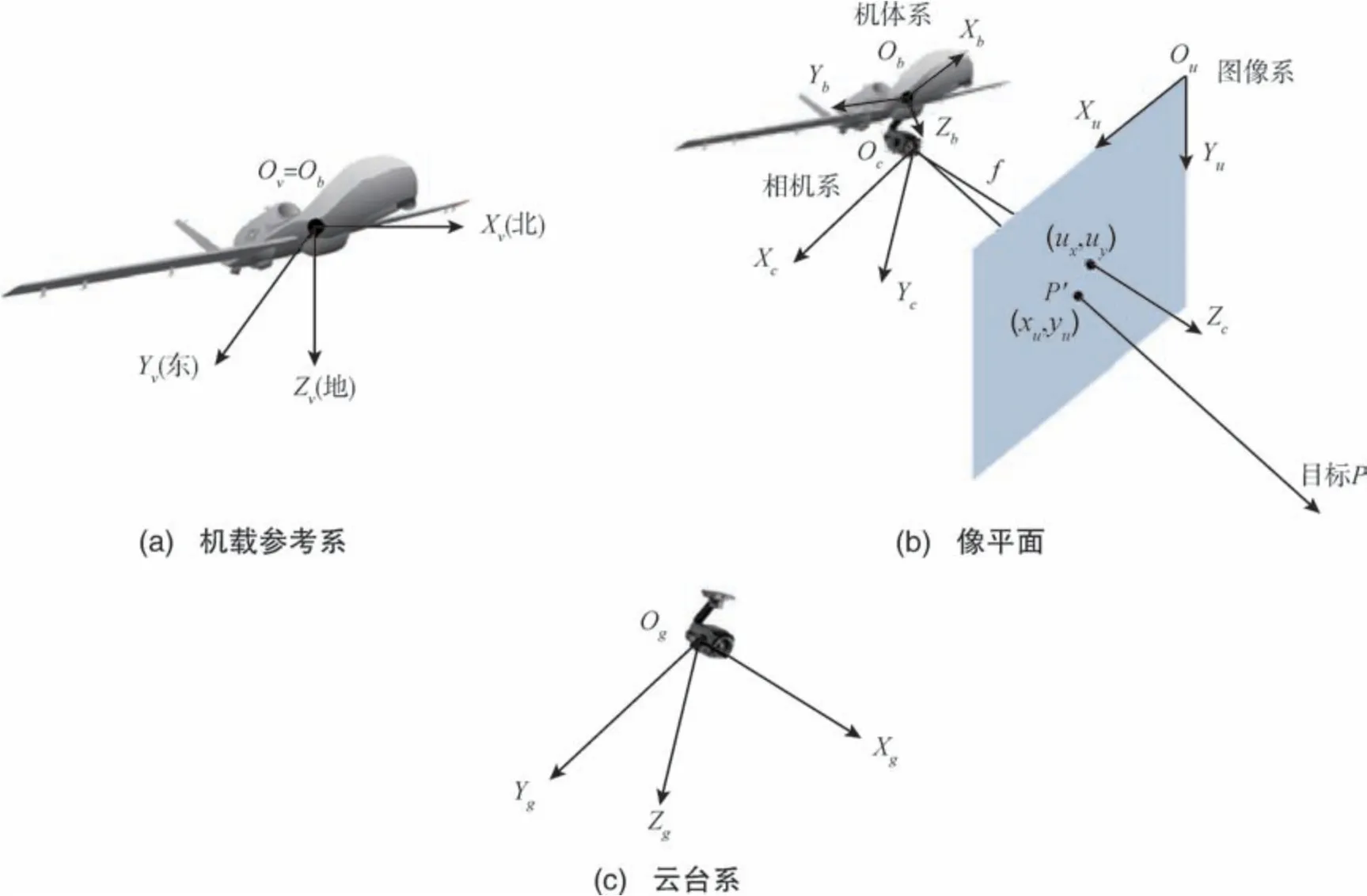
图2 无人机视觉定位相关坐标系Fig.2 Coordinate system related to UAV visual geolocation

（3）机体系

原点取在无人机质心处, 坐标系与飞机固连,X轴在无人机对称平面内平行于机体轴线指向机头,Y轴垂直于无人机的对称平面指向机身右方,Z轴在无人机对称平面内与轴垂直并指向机身下方, 记为Ob-XbYbZb, 如图2（b）所示。

（4）相机系

相机系也叫视线坐标系, 原点为相机的光心,Z轴指向相机视线方向（前方）, 根据小孔成像几何关系,X轴与像平面水平轴在三维空间方向平行指向右,Y轴与平面竖直轴在三维空间方向平行指向下, 记为Oc-XcYcZc, 如图2（b）所示。

（5）图像系

即像素坐标系, 原点是二维矩形图像左上角点,X轴为图像上边沿指向右,Y轴为图像左边沿指向下, 记为Ou-XuYu。 注意, 像平面位于小孔成像几何关系确定的三维空间位置处, 如图2（b）所示。

（6）云台系

相机固连在云台上随之转动, 云台旋转中心即为原点,X轴一般与相机系Zc轴平行同向,Y轴与相机系Xc轴平行指向右,Z轴与相机系Yc轴平行指向下, 记为Og-XgYgZg, 如图2（c）所示。

云台系与相机系的区别有两方面: 一是严格考究, 二者的原点不一定是重合的; 二是相机系和云台系一般分别出现在几何光学和控制领域,二者的X轴、Y轴、Z轴选取遵从各自惯用定义。

1.2 坐标转换关系

已知目标在无人机航拍图像上的投影点坐标（xPu,yPu）、相机内参数K及焦距f、无人机在WGS84 坐标系的位置（Buav,Luav,Huav）、无人机姿态角、相机相对机体的姿态角和位置, 定位任务的目的是求解目标点的大地坐标（BP,LP,HP）。

目标坐标由图像系转换到经纬高坐标系的过程如图3 所示。 其中,依据小孔成像几何原理, 由投影点在图像系的二维坐标计算目标点在相机系的三维坐标, 是两个空间位置点的坐标解算, 随后的过程均是对目标点在不同系的坐标转换。 除e系和大地系外, 其它转换都发生在空间直角坐标系之间, 本文采用齐次坐标转换的方式。 对转换矩阵求逆可获得反方向的转换矩阵, 本文不再赘述。

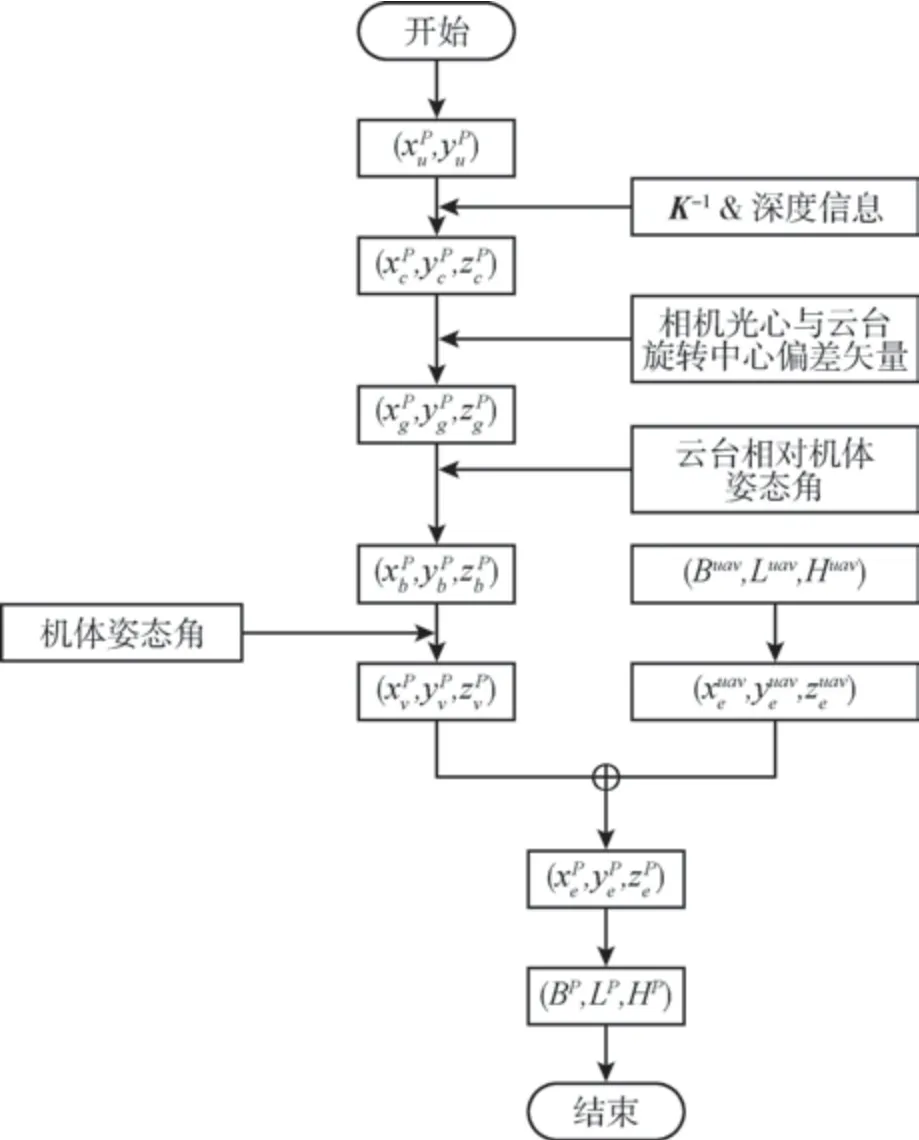
图3 坐标转换定位流程图Fig.3 Flowchart of coordinate transformation geolocation

（1）目标在c系的坐标解算

小孔成像空间定位关系如图4 所示, 设目标点P在图像上的投影点为P'。 在c系中, 设P的坐标为,P'的坐标为; 在u系中, 设P'的坐标为。u系向c系转换是把二维图像系坐标转换为三维相机系坐标, 将图像坐标在末尾添加1 表示为齐次坐标, 即, 则其对应的相机系坐标按如下公式计算

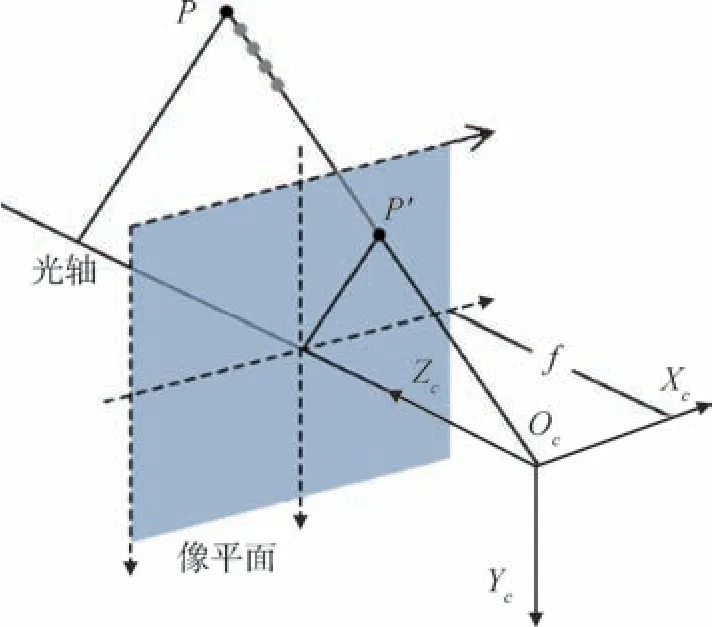
图4 单目视觉几何关系Fig.4 Geometry of monocular vision

要唯一确定P, 需要确定λ的值。

无论从代数或几何的角度看, 由图像系坐标求解相机系坐标均需要提供目标位置的一个额外信息（约束方程）, 即投影过程中丢失的深度信息,这正是单目视觉定位的难点所在。 通常的解决思路是额外估计或光心与目标连线的距离OcP的长度, 或对静止目标采用三角定位的方法（即增加约束方程求解）。

式（1）可变形为

（2）c系向g系转换

从该步开始, 采用齐次坐标转换的方法处理目标点位置在多个空间直角坐标系之间的转换,将三维坐标扩展到四维, 即从开始。c系向g系转换的旋转矩阵为,令为在g系中云台质心指向光心的三维列矢量,一般情况下吊舱都是令二者重合, 偏差忽略不计,即令,O为三维全零列矢量。 则c系向g系的齐次转换为

（3）g系向b系转换

云台相对于无人机的姿态角为（α,β,γ）, 偏航角α为云台Xg轴在b系XbObYb平面内投影与Xb轴的夹角, 右偏为正; 俯仰角β为云台Xg轴与XbObYb平面之间的夹角, 抬头为正; 滚转角γ为g系XgOgZg平面与无人机对称平面之间的夹角, 右滚为正。g系向b系转换的旋转矩阵为

注意, 若云台只有偏航和俯仰两个维度可调,则式（5）中去掉等号右边关于γ角的乘项即可。为b系中无人机质心到云台质心的三维列矢量, 则齐次转换矩阵为

齐次坐标转换具有和式（4）相同的形式, 这里不再重复列出。

（4）b系向v系转换

无人机姿态角表示为（φ,θ,ψ）, 偏航角φ为机体轴在v系XvOvYv（水平）面上的投影与Xv轴之间的夹角, 右偏为正; 俯仰角θ为机体轴与XvOvYv面之间的夹角, 抬头为正; 滚转角ψ为无人机对称平面与通过机体轴的铅垂平面间的夹角, 右滚为正。b系向v系转换的旋转矩阵为

两个坐标系的原点都是无人机质心, 所以没有平移矢量, 则

（5）v系向e系转换

由文献［9］可知,v系向e系转换的旋转矩阵为

（6）e系与大地系之间的转换

在v系向e系转换中需要将无人机GNSS 位置（大地系下的坐标） 转换到e系中得到, 根据文献［10］, 转换方法如下

其中,

最终, 目标在e系下的坐标按如下方法转换为大地系坐标

2 单机对地视觉定位关键技术与研究现状

单架无人机挂载光电载荷对地视觉定位是目前的主流方式, 也是多架无人机协同的技术基础,相关研究较多。 目前的主要方法可分为四种类型,分别是基于辅助地理信息的定位、已知目标距离的定位、三角定位和纯角度滤波定位。 按前文对技术手段的粗分类, 这里的前两类属于基于补充额外信息的定位, 后两类属于对多个角度观测数据采用统计方法估计位置的定位。

2.1 基于辅助地理信息的定位

常用于辅助视觉定位的地理信息数据是数字高程模型（Digital Elevation Model, DEM） 和数字地表模型（Digital Surface Model, DSM）［11］。 DEM 是地形表面形态的数字化表示, 是将地面划分为网格,用网格坐标（x,y,z）表示实体地面模型, 其中的z表示高程数据。 DSM 是在DEM 基础上进一步包括了地面上所有固定物体, 如建筑、森林、桥梁等在内的高程模型, 通常DSM 可与正射影像结合,也就包含了图像特征信息。

基于辅助地理信息的对地视觉定位思路为:求目标在图像上的点与光心连线和DEM/DSM 模型交点的坐标。 因为相机的内外参数均已知, 即可确定连线方向, 因而可以求解交点。 定位原理示意图如图5（a）所示［12］; 求解交点通常是利用迭代计算直至收敛的方法, 迭代计算过程与利用割线法对连续函数求根一致, 如图5（b）所示［13］。 联系1.2 节c系的坐标解算容易看出, 该类方法从几何角度理解很直观, 求解线和面的交点; 从代数角度看, 相当于增加了一个约束方程。 采用该方法定位的工作包括文献［13］ ～文献［18］等。

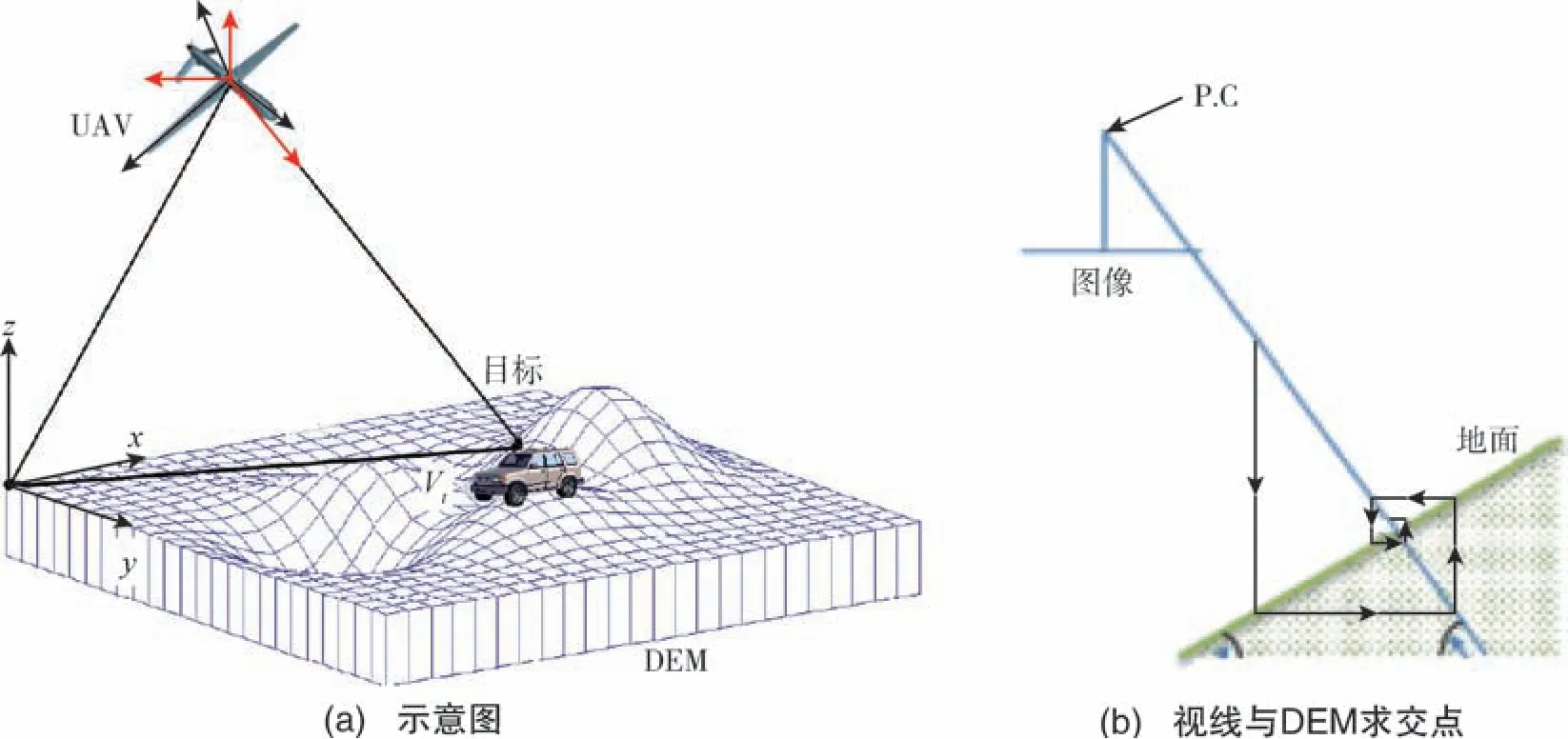
图5 基于DEM 的定位Fig.5 Schematic diagram of geolocation based on DEM

部分算法利用DSM 校正后的图像特征进行定位。 文献［13］、文献［19］ ～文献［21］对无人机实拍图像提取SIFT 特征、SURF 特征或CNN 特征, 与参考图片的特征进行匹配, 根据匹配点几何约束修正无人机导航参数再解算目标点位置, 或者直接在参考图上匹配定位目标。 文献［22］提取实拍图像特征与DSM 正射影像特征匹配, 计算单应（Homography）矩阵, 将目标映射到参考图像上, 直接提取经纬高。 文献［23］用Sobel 算子提取参考图线特征保存于无人机中, 与相机拍摄的图像经过相同处理后配准, 即可得到目标位置, 该方法假设地面是水平的, 并且通过气压测高仪获得无人机和地面的相对高度。 文献［24］对无人机视觉导航定位中的配准定位算法有详细总结, 该类方法主要用来确定无人机自身的位置, 用于定位目标的研究比较少, 不是对地视觉定位的主流方法。

基于地理信息支持的定位方法优点是基于一次观测即可对静止或运动目标定位, DSM 模型的图像特征信息还可以用于改进定位精度, 缺点则是先验地理信息数据通常难以获得。

2.2 已知目标距离的定位

由1.2 节c系的坐标解算可知, 若是能给出成像时丢失的某一个维度的深度信息, 则可以直接计算得到目标位置, 这是实践中运用最为广泛的一类方法。 这类方法原理上相当于增加了一个目标三维坐标的约束方程, 结合式（1）由图像坐标系反解到相机系, 再经过一系列坐标系转换求得参考系下的坐标值。 相关研究算法非常多, 对坐标系的定义不同, 具体求解公式不同, 但思想是一致的。 下面依据本文设定的坐标系, 给出原理性公式描述, 并梳理主要方法。 常用的补充距离信息包括以下三种:

（1）已知目标海拔高度

这类方法通常假设目标区域地面平坦, 则可用测量区域内某个参考点的高度值近似目标高度,参考点的高度可以通过GNSS 测量或者DEM 查询获得。 无人机海拔高度由GNSS 实时可查, 所以等效于已知目标与无人机之间的高度差, 用h表示。也可以直接获得高度差, 例如通过气压计测量大气压强差再转化为高度差。 其中, 文献［25］、文献［26］不需要从无人机状态传感器来测量高度差,而是通过立体视觉的方法估计高度差。

文献［28］ ～文献［32］均采用此类方法, 此类方法优点是只需一次测量即可确定目标位置, 适用于运动和静止目标, 缺点是精度不高。 更进一步的研究采用多次测量的统计估计方法, 对于静止目标, 通常采用回归分析、最小二乘等方法, 对于运动目标, 则建立运动状态方程和测量方程,采用Kalman 滤波等方法进行估计。 对静止目标的多次测量通过统计估计的方法定位, 基本思想就是建立如式（14）等号右边所示的多个测量方程, 利用统计方法求解最优三维位置坐标。 如文献［33］ ～文献［35］采用迭代最小二乘（Recursive Least Squares, RLS）、误差滤波、Monte Carlo 等方法减小误差; 文献［36］、文献［37］采用回归分析的方法在定位的同时估计方位角偏差, 提高估计精度,同时考虑无人机航迹优化, 提高测量精度; 文献［24］、文献［27］、文献［38］、文献［39］用扩展Kalman 滤波（EKF）提高估计精度, 同时提出规划路径和云台控制等提高精度的方法; 文献［40］、文献［41］采用容积Kalman 滤波（CKF）算法进行估计;相似的工作还包括文献［42］ ～文献［46］, 上述算法都是补充海拔高度测量值的统计方法。

（2）已知目标斜距

随着无人机载荷技术的进步, 越来越多光电吊舱具备主动激光测距能力, 可以直接测量目标到光电吊舱的精确斜距。 激光测距指向和视场中心同向, 因此斜距就等于, 可代入式（1）中解算目标位置, 这种方式不需要额外测量目标高程,不需要假设地面平坦。 文献［8］、文献［47］、文献［48］均是通过激光测距获得斜距, 并进一步解算或滤波估计目标位置。

（3）已知目标尺寸

在某些情况下, 已知目标某一个维度的绝对尺寸, 通过图像处理的方法能够计算得到无人机与目标之间的相对高度, 从而按照前面所述已知高度差的方式定位目标。 如文献［49］提出的定位方法, 已知目标（车）的长度, 在其处于水平状态时,通过测量车头、车尾之间的像素距离, 可求解出目标相对于无人机的高度差, 从而再利用文献［33］中的算法对目标进行定位, 如图7（a）所示。 图7（b）为其几何原理, 已知PQ尺寸, 则根据ΔGHP、ΔGHQ和ΔGPQ的关系, 可以求解出GH的长度。

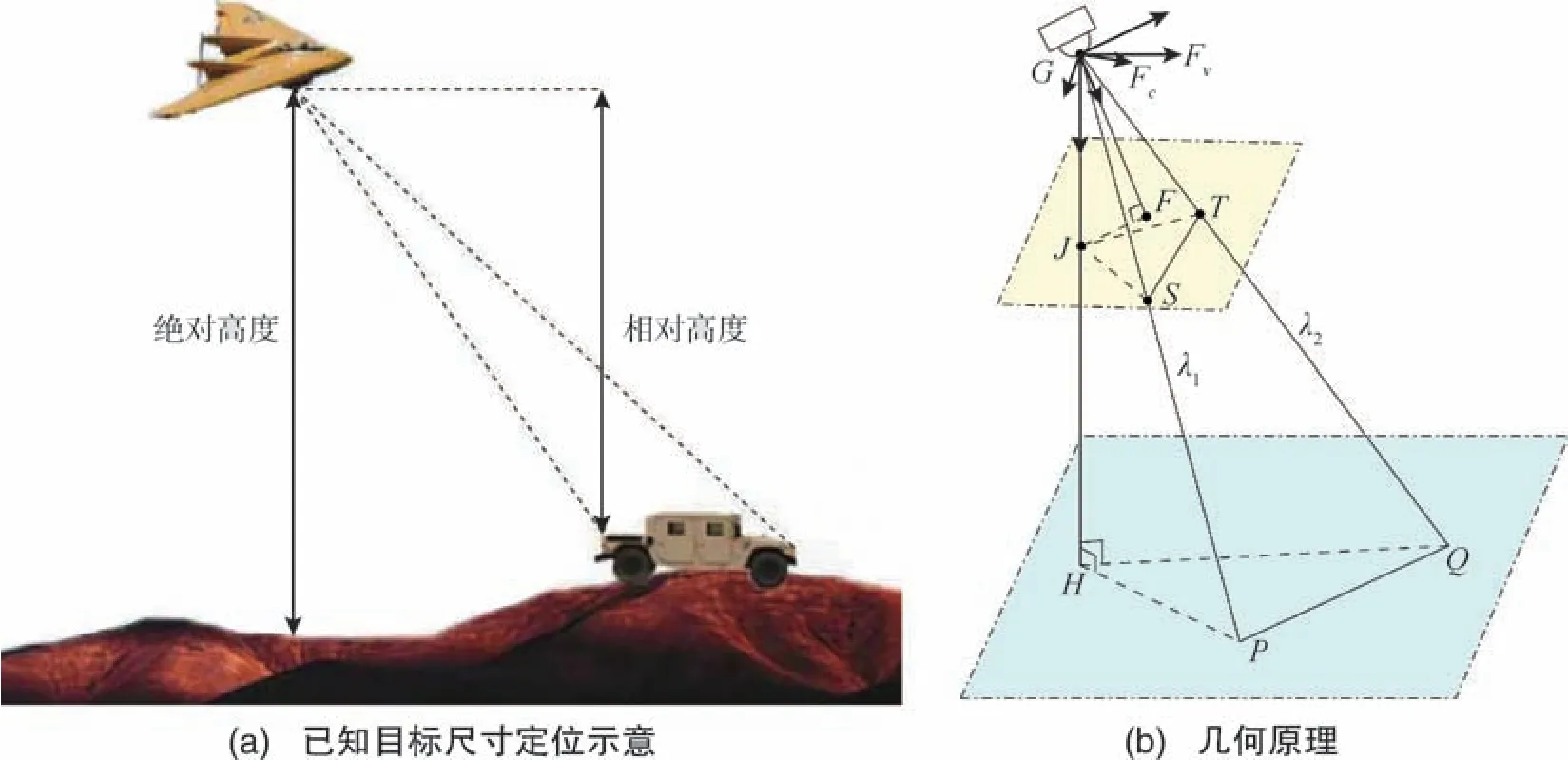
图7 已知目标尺寸的定位Fig.7 Schematic diagram of geolocation based on target size known

2.3 三角定位

三角定位利用目标的两个或多个不同方向角测量值来计算目标位置, 原理是目标与两个测量点构成三角形。 已知两参考点的坐标以及参考点与目标点连线方向矢量, 则可以唯一确定目标点坐标, 如图8（a）所示［50］。 实际应用中, 由于无人机和目标相距较远且各类误差叠加, 两个参考点处测量值估计的定位误差较大, 通常对多次测量进行滤波或非线性优化求解以减小定位误差, 如图8（b）所示［50］。 文献［50］、文献［51］ 采用非线性Kalman 滤波的方法估计最优位置, 文献［52］采用Levenberg-Marquardt 非线性优化的方法求位置最优解。 采用该方式定位的无人机通常绕目标点进行盘旋飞行, 多次观测, 最优路径规划也是一个重要研究点。 对于单个无人机单相机而言, 该方法只能定位静止目标, 因为需要无人机运动到不同 位置对同一点进行观测。

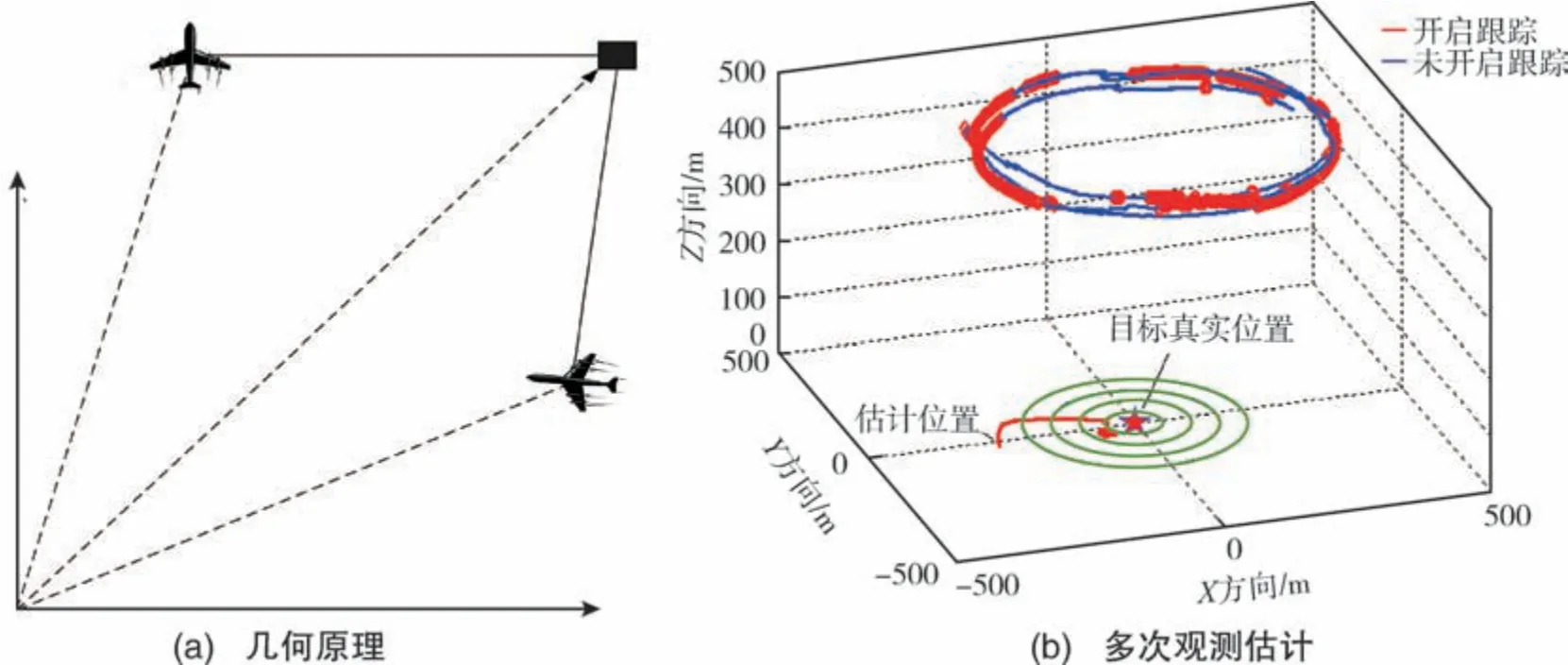
图8 三角定位Fig.8 Schematic diagram of geolocation based on triangulation

2.4 纯角度滤波定位

纯角度跟踪是指仅由测量点到目标点的方向角测量值估计运动目标的位置和速度, 常用于无源定位领域, 如被动雷达、声呐或光学定位［53］。由于丢失深度信息, 单目光学定位处理的也是纯角度测量问题, 部分研究采用纯角度滤波的方法对运动 目 标 进行 跟踪 定 位, 如 文献［54］ ～ 文献［57］。

纯角度滤波问题的核心是建立目标运动状态方程和观测方程, 从而通过Kalman 滤波方法估计目标状态。 对地定位问题一般建立线性运动状态方程和非线性观测方程, 具体如下

式（15）中, 目标状态矢量x为目标位置和运动速度,wk为状态转移误差（可描述随机加速度）,非线性测量函数hk（xk） 为k时刻无人机的测量值（一般包括目标图像坐标、各种无人机传感器状态参数等）,vk为观测误差, 以上误差一般采用Gauss 分布。 在建立了目标运动状态方程后, 可以采用经典非线性Kalman 滤波方法如EKF、UKF、CKF 等来估计目标状态。

地基无源雷达对空目标跟踪是经典的纯角度跟踪应用, 该场景中测量平台静止, 且目标背景简单, 因而跟踪精度较高。 而在无人机对地视觉定位应用中, 测量平台和目标都在运动, 尤其是目标在地表运动, 随机误差更大, 这种纯角度滤波定位方法精度不高。

3 多机协同对地视觉定位研究现状

多机协同对地视觉定位方法主要有两种, 一种是多机三角定位, 一种是多机融合滤波定位,后者也包括了在纯角度测量值的基础上辅以额外信息的方法。

多机三角定位是单机三角定位方法的直接扩展, 相比于单机, 在满足同时测量的条件下可以定位静止以及运动目标。 这类方法通常是中心化的, 多架无人机将其观测同一个目标的测量数据传送到一个中心节点, 利用各无人机状态确定多个视线方向, 则交汇点就是目标位置。 文献［58］、文献［59］分别采用两架或多架无人机目标视线交汇求解目标点位置, 利用最小二乘、自适应Kalman滤波等方法对多个观测估计最优值。

相比于单机, 多机融合滤波定位有更多测量数据, 能够获得更高的精度, 同时多机协同更容易识别目标, 多机融合分为中心化与非中心化两种。 以单个目标为例, 目标状态方程如式（15） 所示, 目标测量方程个数由无人机架数决定, 每架无人机对应一个如式（15）所示的测量方程, 在中心节点汇成总的测量方程。 文献［60］ ～文献［68］较早研究了多架无人机融合滤波对地定位, 广泛采用Kalman 滤波、粒子滤波和信息滤波等多种滤波方法, 在滤波过程中通过估计通信延时和偏差, 或引入更多观测量, 或非中心化处理等方式提高位置估计精度。 文献［69］侧重研究多个无人机如何调整队形跟踪目标。 文献［70］ ～文献［72］提出分布式无人机传感器资源管理方法以及单架无人机吊舱姿态角控制方法, 保证多个目标尽可能地在视场中。 文献［73］引用文献［33］的方法先让每一架无人机对自身看到的目标进行定位, 再利用多假设检验、对转换矩阵误差进行融合滤波等方法提高估计精度。

目前, 多机协同对地视觉定位方法主要处理单一目标, 回避复杂的多目标数据关联问题, 因而主要是对单机方法的直接扩展。

4 展望与结论

随着基于深度学习的计算机视觉技术飞速发展, 为光电吊舱赋予智能目标检测与跟踪能力成为当下的研究和应用热点。 目前, 中小型无人机已经实现了嵌入式AI 边缘计算平台的部署, 具备机载端在线实时多目标检测与跟踪能力［32］。 由于不需要人工操作, 目标定位算法可实现实时多目标定位, 从而具备与决策系统全自主衔接的能力,极大地提高了无人机感知的反应速度, 提高了无人机智能化水平, 强化了无人机在军事和民用领域的应用能力。 多目标定位的智能化是未来的一个重要研究方向。

在军事上, 无人机“蜂群战” 的概念及相关技术已经成为美军的重要战略布局, 实质是以大规模、低成本无人机集群为主体实现跨域分布式协同作战。 基于视觉的协同感知是分布式协同的重要组成部分, 协同目标识别和定位是其主要任务。 协同必然涉及多源信息融合, 在多目标任务中, 数据关联是影响融合效果的重要方面, 准确的识别判断和精确的定位能够提高数据关联的准确率, 从而提高后续识别和定位精度, 二者是一个耦合的过程。 因此, 与多源数据关联和识别相耦合的多源多目标协同定位技术是未来无人机视觉对地定位的一个重要研究方向。

当前, 无人机光电吊舱通常配备具有高倍变焦功能的相机以观察远距离小目标, 其定位原理是把目标放到视场中心, 令目标的方向角与吊舱视线轴指向重合, 从而规避相机内参数。 若要实现视场内多个目标的同步定位, 对于非视场中心的目标, 内参数必须参与计算过程。 变焦相机标定研究由来已久［74-75］, 无人机吊舱变焦镜头通常具有视场大、变焦倍数大的特点, 变焦相机标定方法在无人机吊舱领域的应用和研究未来必将成为一个重要的研究方向, 以支撑无人机光电吊舱定位技术。

无人机飞控传感器精度有限, 尤其是小型低成本无人机, 在此条件下以提高定位精度为目标的研究也是一个重要方向。 该方向可从两方面开展研究, 一是通过更加合理的航迹规划［37-38,67］特别是多机协同规划来提高定位精度; 二是融合多源传感器提高定位精度, 尤其是主动激光雷达、微波雷达等。

综上所述, 受益于计算机视觉智能的跨越式提升, 无人机将具备实时精准的多目标识别与跟踪能力、高效的飞行控制与协同能力以及多模态异构传感器信息融合能力, 无人机视觉地理定位技术未来将向着多目标、高精度和高可靠性地理定位方向发展。