基于非线性虚拟材料法的栓接结合部动态特性分析

李 鹏, 杨 成, 刘秀宇, 魏 超, 吴齐运

（北京航天控制仪器研究所, 北京 100039）

0 引言

栓接结合部对航天器的影响表现为使箭体结构及箭载设备的整体刚度降低和阻尼增加, 经栓接形式连接的构件及仪器仪表整体刚度中30% ～50%决定于结合部的刚度特性, 阻尼90% 以上来源于结合部。 栓接结合部的力学行为显著影响到航天器及武器装备的结构安全和可靠性, 影响搭载仪器的稳定输出。 在栓接结合部研究领域, 学者们分别从宏观和微观角度对栓接结合部动静态特性进行了大量研究, 涉及航空航天、汽车工业、数控加工等诸多领域［1-5］。 子结构耦合方法［6-7］是辨识栓接结合部刚度、阻尼的主要方法之一, 然而该方法辨识结果易受测试噪声影响, 且难以建立栓接结合部刚度、阻尼与接触面积、预紧力等因素之间的函数关系, 因此辨识结果难以被应用于栓接形式的分析与优化。

由于传统辨识方法的不足, 国内外学者则从微观角度去研究栓接结合部的接触机理。 1966 年,Greenwood 等［5］将微观表面形貌上微凸体的高度分布看作随机变量, 提出了著名的基于统计学分析的GW 接触模型。 GW 接触模型假设: 微凸体的峰顶是球形, 具有相同的曲率半径, 微凸体高度服从高斯分布, 表面粗糙度各向同性, 微凸体弹性接触且变形相互独立。 1991 年, Majumdar 等［4,8-9］基于机械加工表面具有自仿射分形特征提出了包含分形维数D和分形粗糙度参数G的M-B 模型。M-B 模型指出: 结合面承受的负载越小, 塑性变形的比例越大。 其研究获得了真实接触面积的表达式, 并估算了从弹性变形转变为完全塑性变形的临界粗糙体尺寸。 研究结果表明: 尺寸较小的微凸体产生塑性变形, 而尺寸较大的微凸体则产生弹性变形。 2010 年, Jiang 等［10］利用分形几何和赫兹接触原理对三种不同加工方式（铣削、磨削、刮研）下的粗糙表面形貌、微凸体弹塑性形变以及单个微凸体接触刚度进行了研究, 利用构造函数方法计算出表面轮廓的相关参数, 理论计算得出的接触刚度与不同载荷下实验获得的刚度是一致的, 证明了其模型的合理性。 温淑花等［11-12］在对粗糙表面分形理论和球体与平面接触刚度问题研究的基础上建立了具有尺寸独立性的结合部法向和切向接触刚度分形模型, 通过对该模型的仿真分析得出法向和切向刚度与结合部外载荷的非线性关系。 2012 年, 黄开放等［13］通过计算特定螺栓预紧力下虚拟材料模型各项参数, 验证了采用虚拟材料方法模拟栓接结合部的可行性。 2013 年, 基于赫兹接触理论及分形几何理论, 田红亮等［14］考虑结合部法向和切向特性之间的相互作用, 推导出虚拟材料的弹性模量、泊松比等材料属性, 但是没有考虑虚拟材料的非线性特征。 2017 年,De Filippis 等［15］采用子空间算法推导接触区非线性回复力, 解释了飞机机翼与油箱间因螺栓连接导致的模态相互作用现象。

基于分形接触理论和赫兹基础理论, 本文推导出了非线性虚拟材料的等效弹性模量、泊松比和密度特征参数与接触应力的函数关系。 采用有限元方法获得栓接结合部接触表面应力分布, 建立栓接结合部非线性虚拟材料模型。 设计L 形试件验证所提出模型的有效性, 通过对比理论与试验结果可知, 所提出模型能够准确地反映栓接结合部的动态特性, 验证了模型的有效性。

1 栓接结合部非线性虚拟材料模型

1.1 传统虚拟材料建模方法

目前对结合面刚度与阻尼的研究较多, 但这些刚度与阻尼数据难以直接应用于实际工程中,且与试验相比精度较低。 刚度与阻尼不是材料的固有属性, 而弹性模量、剪切模量、泊松比、密度是材料的固有属性。 因此, 虚拟材料法可以用来研究栓接结合部的接触问题, 由于栓接结构在结合部处可以看作是由很多微凸体相互接触而成,该方法是把微凸体接触的部分看作是一层厚度相同的虚拟材料层, 其模型如图1 所示。 虚拟材料模型具有建模简单和较传统统计模型具有贴近结合部接触机理、准确性、普遍性等优点, 但机加工表面的一些物理参数譬如粗糙度、波纹度、平面度等与虚拟材料相关, 但是虚拟材料方法忽略了这些因素的影响。

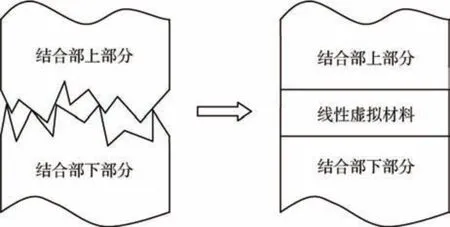
图1 结合部虚拟材料模型示意图Fig.1 Schematic diagram of virtual material model at bolted joint

模态分析中, 虚拟材料的固有属性即弹性模量E、剪切模量Gx、泊松比v和密度ρ。 依据文献［16］,虚拟材料的特性参数中, 弹性模量和剪切模量只发生在微凸体发生弹性变形阶段, 可用如下理论公式计算得出

式（1） ～式（5）中,D为分形维数,G为分形粗糙度参数,ψ为分形维数D决定的域扩展因子,aL为微凸体最大接触面积,ac为微凸体临界接触面积,E'为当量弹性模量,E1、E2为接触体的弹性模量,v1、v2为接触体的泊松比,v'为当量泊松比,E*为无量纲的虚拟材料弹性模量,为无量纲的虚拟材料剪切模量,ρ1、ρ2为两接触材料的密度,l1、l2为两接触表面实体的厚度。

式（1）、式（3）和式（4）中的参数计算公式分别为

式（6） ～ 式（10） 中,Ar为真实接触面积,为硬度和屈服强度相关系数,为材料特性,H、σ0.2分别为较软材料硬度和屈服强度,G'为当量剪切模量,G1、G2为两接触体材料的剪切模量。

1.2 非线性虚拟材料栓接结合部模型

本文提出的非线性虚拟材料接触模型是在图1右侧所示的线性虚拟材料模型基础上将微凸体接触部分替换为非线性虚拟材料, 通过对非线性虚拟材料相关材料属性的定义推导及计算, 进而构建成栓接结合部非线性虚拟材料模型。

本文将以最大平截面积a'L为自变量, 通过对非线性虚拟材料弹性模量、泊松比、密度及材料应力的计算, 推导计算出虚拟材料固有属性。 虚拟材料的弹性模量、泊松比、密度表现出非线性特性, 即随着应力的改变而改变。 弹性模量、泊松比、密度的非线性体现在两方面: 随着结合部整体外载荷改变引起的应力改变, 虚拟材料弹性模量、泊松比和密度随之改变; 当外载荷一定时,虚拟材料内部因为应力分布不均导致材料各个部分弹性模量、泊松比和密度也各不相同。 本文还推导出了非线性虚拟材料的应力-应变曲线, 进一步证实并说明了虚拟材料的非线性特征, 虚拟材料的本构模型可用于有限元软件分析, 弥补了商用软件在接触力学分析上的不足。

1.3 栓接结合部的弹性模量、泊松比和密度

由于机加工表面具有分形的特性, 因此分形理论已经被国内外许多学者应用到栓接结合的研究中, Wang 等［7］提出了可以用W-M 函数来表征机加工表面特性, 粗糙表面微凸体平截面积的统计学分布函数满足

式（12）中,a'为单个微凸体的平截面积, 且有a'=2a,a为单个微凸体的实际接触面积,为最大接触面的平截面积。 区别弹性变形和塑性变形的临界接触面积可写为

两个粗糙表面栓接在一起, 实际上可以看成是很多不同大小微凸体的接触, 如图2 所示。

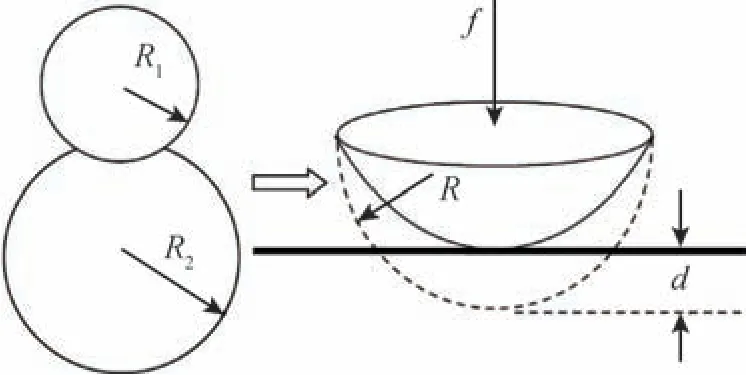
图2 两个球形微凸体接触转化为球体与刚性平面接触模型Fig.2 Schematic diagram of two spherical asperities contact model transform into spherical-rigid base contact model

图2 中, 左侧有两个半径为R1和R2且接触的弹性球体, 而两个球体的接触问题又可以等效转化为弹性球体和刚性平面的接触问题。 一个半径为R的弹性球体, 在外力f作用下与一个刚性平面接触并产生形变, 弹性球体产生的形变量为d,由赫兹弹性接触理论可知, 当微凸体只发生弹性变形时, 法向力f和接触面积a分别为

对于单个微凸体, 可得接触应变ε的函数

式（15）中,d和R分别为单个微凸体的变形和等效曲率半径。

单个微凸体的应力函数可表示为

已知单个微凸体的应力和应变函数, 依据弹性模量的定义, 单个微凸体的弹性模量可写为

由分形理论可知, 单个微凸体的变形量和等效曲率半径分别为

将式（18）和式（19）代入式（17）中, 单个微凸体的弹性模量可重新表示为

加权平均弹性模量和相应的实际接触面积可获得虚拟材料的等效弹性模量, 当微凸体发生塑性变形时, 弹性模量为零; 当微凸体只发生弹性变形, 即平截面积满足a'c＜a'＜a'L时, 可获得等效弹性模量

式（21）中,A0为名义接触面积。 将式（12）代入到式（21）中, 结果为

式（23）中,β为剪切力和预紧力之比,fτ为静摩擦系数。

依据接触表面剪切刚度、剪切变形和剪切力之间的关系, 加权平均剪切模量和相应的实际接触面积可获得虚拟材料的等效剪切模量, 当平截面积a'满足时, 对式（23）积分, 已知剪切模量和相应的实际接触面积可获得虚拟材料的等效剪切模量

栓接结合部由表面微凸体组成, 结合部的质量只是很小的一部分。 因此, 虚拟材料的密度对栓接结合部的动态特性影响较小。 依据真实接触面积与名义接触面积之比, 提出一个简化等效密度定义

1.4 栓接结合部的接触应力

假设: 在整个名义接触面积A0上, 接触应力均匀分布, 则平均接触应力σV为平均弹性微凸体接触应力σt与平均塑性微凸体接触应力σs之和。

当平截面积满足a'＞a'c时, 即微凸体发生弹性变形时, 此时单个微凸体的法向力可表示为

将式（12）、式（27）代入式（28）中, 可得

将式（12）、式（30）代入式（31）中, 可得接触表面的塑性应力

最终, 可得非线性虚拟材料的平均接触应力

2 非线性虚拟材料的验证

2.1 非线性虚拟材料模型试验验证

为了验证所提出模型的准确性, 考虑航天器常用的栓接形式, 本文设计了L 形组合件, 尺寸参数如图3 所示, 所用L 形试件厚度为20mm。 设计的L 形组合件具有不对称的特性, 在模态试验中通过求解振型及各阶频率, 可以很好地体现结合部特性。 L 形组合件为两个相同尺寸、相同加工方式的L 形件通过螺栓装配组成, 如图4 所示, 图中蓝色部分表示的是根据虚拟材料模型理论添加的可在有限元模型中表示结合部特性的结构层。在结合部垂直方向均匀布置2 个φ16 的孔, 其编号为1 和2, 该L 形件分形维数D=1.28, 分形粗糙度参数G=3.5 ×1012, 域扩展系数ψ=2.04, 复合弹性模量E*=92GPa。

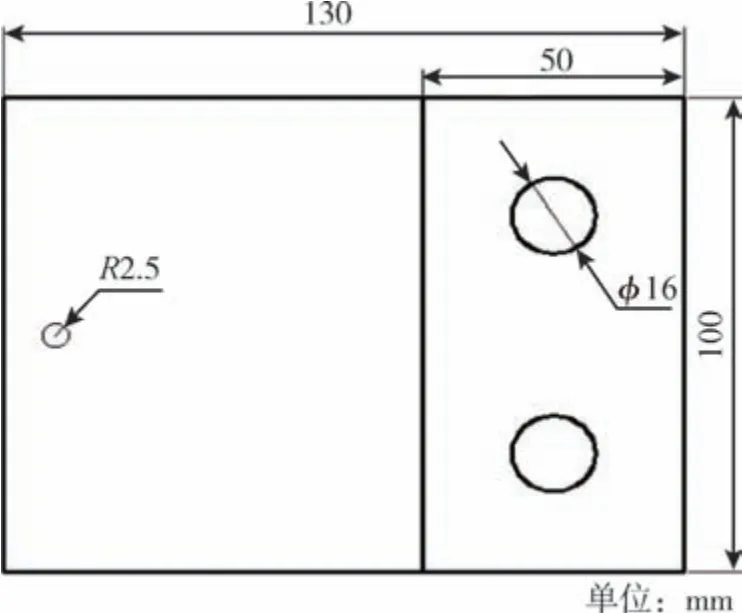
图3 L 形试件尺寸Fig.3 Dimensional diagram of L-shaped specimen

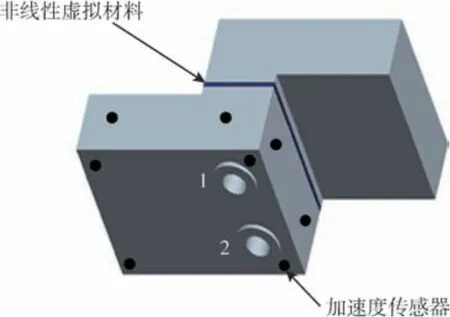
图4 L 形试件组合体Fig.4 Schematic diagram of L-shaped specimen assembly

L 形件的材料为球墨铸铁, 型号为QT600-3,通过磨削加工获得粗糙表面, 其粗糙度为Ra=1.6μm, L 形件的材料属性如表1 所示。 为了精确获得栓接结合部的动态特性, 试验过程中L 形组合件被绳索吊起以模拟自由模态, 利用8 个加速度传感器（型号为PCB Model330B30）分别测试试件三个方向的振动数据, 图4 展示了单个试件上传感器的布置情况, 另一个试件的传感器布置与其对称。采用力锤提供激振力, 连续敲击8 次, 将振动数据和力锤数据采集并利用LMS Test. Lab 振动噪声测试系统进行数据分析, 得到L 形组合件各阶模参数和振型。 试验过程中为最大限度消除实际噪声等各种外在因素的影响, 提高信噪比, 在一定的预紧力情况下, 试验反复重复测试6 组, 取加权平均值作为最终的实际数值。

表1 L 形件的材料特性参数Table 1 Material properties of L-shaped specimen

（1）传统虚拟材料模型试验验证

在传统线性虚拟材料方法中, 虚拟材料层的厚度应保持不变, 本文选择厚度为0.1mm 的虚拟材料层作为研究对象。 在试验过程中, 两个螺栓提供相同的预紧力F=10kN, 采用传统虚拟材料模型可以计算出虚拟材料的平均应力、等效弹性模量、泊松比和密度, 如表2 所示。

表2 传统虚拟材料法的特征参数Table 2 Characteristic parameters of traditional virtual material method

利用ANSYS 有限元软件对L 形组合件进行建模和静力学分析, 获得栓接结合部各节点压强值。通过Matlab 软件, 根据各节点的压强值计算出各节点对应接触刚度和接触阻尼值, 通过MATRIX27矩阵单元建立栓接结合面节点-节点的接触刚度和接触阻尼单元。 结合面之间采用目标面单元为TARGE170 单元、接触面单元为CONTA174 单元进行柔-柔面接触, 选择初始绑定, 其他条件默认。

将有限元仿真分析得到的固有频率与力锤敲击试验所得到的固有频率进行对比, 如表3 所示。结果表明: 传统虚拟材料方法与试验结果的误差均在10%以上, 误差较大, 传统线性虚拟材料模型不能够准确地表征栓接结合部的动力学特性。该方法的不足之处在于没有考虑螺栓分布对结合部动态特性的影响, 忽略了栓接结合部表面非线性的特点。

表3 L 形组合件均布预紧力下试验模态与普通虚拟材料模态Table 3 Test modal and common virtual material modal for L-shaped specimen assembly under uniformly distributed preload

（2）非线性虚拟材料模型试验验证

栓接结合部的动态特性影响因素不仅仅包括虚拟材料的特征参数, 还包括虚拟材料的厚度。本文引用等效刚度方法［17］来获得虚拟材料的厚度,假设在整个名义接触面积A0上的平均压强分布为PE, 力F和虚拟材料变形δ及栓接结合部刚度的函数关系可表示为

式（34）中,E为虚拟材料的等效弹性模量,h为虚拟材料的厚度,KN为栓接结合部的法向接触刚度。 根据文献［18］, 其表达式为

依据式（34）, 虚拟材料厚度为

虚拟材料的厚度和弹性模量成正比关系, 和接触刚度成反比关系。 根据等效刚度方法, 可以推出虚拟材料厚度和接触压强的函数关系, 如图5所示。

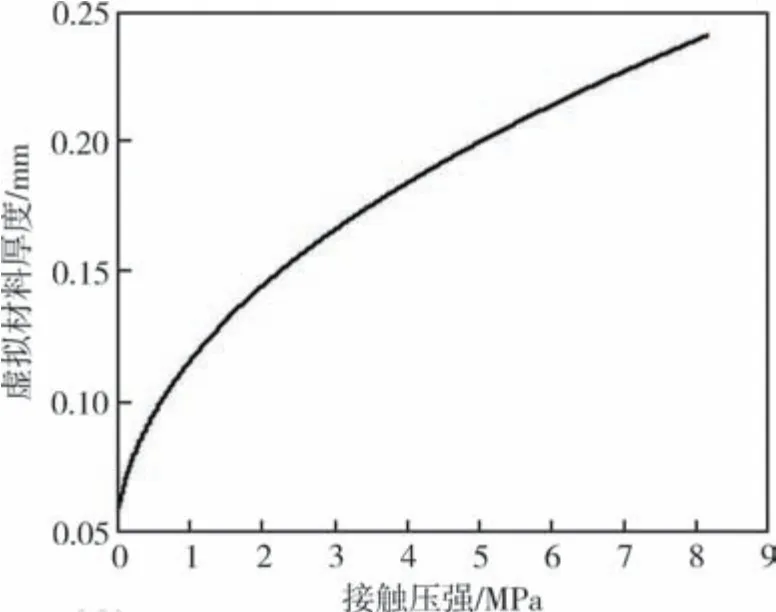
图5 虚拟材料厚度和压强的关系Fig.5 Relationship between virtual material thickness and contact pressure

由图5 可知, 虚拟材料的厚度随着接触压强的增大而增加。 为了建立栓接结合部非均匀压强分布的模型, 整个接触表面的虚拟材料层厚度应该保持一致, 故选择厚度为0.1mm 的虚拟材料层作为研究对象。

2.2 非线性虚拟材料模型有限元分析

对L 形组合件进行静力学分析, 获得的栓接结合部的应力分布情况如图6 所示。

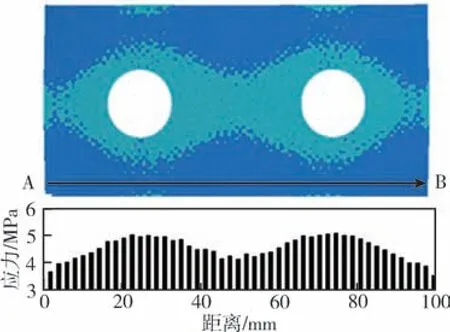
图6 结合面的应力云图和AB 线上的应力分布Fig.6 Stress nephogram and stress distribution on AB line of L-shaped specimen assembly bolted joint

从栓接结合部中选择一条直线AB, 当每个螺栓预紧力为10kN 时, 栓接结合部的应力分布呈现不均匀的特性, 靠近螺栓孔的位置应力最大为5.1MPa, 而在远离螺栓孔的A 点接触应力值最小为3.2MPa。

在理想情况下, 结合部虚拟材料由于具有非线性, 因此材料处处弹性模量均不相等。 如果能利用所得到的连续且各点不相等的弹性模量进行模态分析, 则可完全达到分析非线性虚拟材料模态情形的效果。 但由于受有限元分析软件的限制,本文设计了折中方案, 即根据集合面静力分析得出的应力分布情况将中间虚拟层划分为数个区域。在试验过程中, 由于每一个螺栓的预紧力是相同的, 因此压力分布是对称的。 为了研究栓接结合部虚拟材料的非线性特性, 把栓接结合面的一半分成7 个区域, 如图7 所示, 以此来近似逼近材料非线性效果。

图7 结合面的虚拟材料区域划分Fig.7 Virtual material areas division of L-shaped specimen assembly bolted joint

在有限元模型中, 根据栓接结合部非线性虚拟材料不同区域的压强值可以获得对应的非线性虚拟材料参数, 如表4 所示。 最后进行栓接结合部结构动力学仿真分析, 获得栓接结合部的动态特性, 并且通过与传统虚拟材料法分析结果进行对比, 验证模型的准确性。

表4 L 形试件结合部虚拟材料的特征参数Table 4 Characteristic parameters of different L-shaped specimen bolted joint virtual material areas

将有限元仿真软件分析得到的1 ～3 阶振型图与力锤敲击试验所得到的振型图进行对比, 结果如表5 所示。 可以发现, 仿真结果和试验结果各阶振型均高度吻合。

表5 L 形组合件有限元及试验振型Table 5 Finite element analysis and test vibration mode of L-shaped specimen assembly

2.3 结果对比

传统线性虚拟材料法和非线性虚拟材料法的试验结果和理论结果如表6 所示。 非线性虚拟材料法三阶模态误差分别为3.10%、8.80%、2.20%,其误差小于传统线性虚拟材料法12.98%、12.60%、-10.50%的结果, 表明非线性虚拟材料法可以更好地表现出结合部在受外载荷情况下的模态特性。

表6 L 形组合件均布预紧力下试验模态及普通虚拟材料、非线性虚拟材料模态Table 6 Test modal, common virtual material modal and nonlinear virtual material modal for L-shaped specimen assembly under uniformly distributed preload

3 结论

考虑到栓接结合部的动态特性对航天器结构可靠性以及箭载仪器仪表的输出精度都有重要的影响, 故本文基于分形理论提出了一种基于非线性虚拟材料法的栓接结合部模型。 通过对模型研究, 可得出以下结论:

1）本文将传统中对结合部的刚度、阻尼的研究转化为对结合部的非线性虚拟材料固有属性的研究, 该模型将结合部看作由结合部上部分、结合部下部分及中间非线性虚拟材料层组成, 基于分形理论和赫兹接触理论, 计算出非线性虚拟材料的等效弹性模量、泊松比和密度特征参数, 并研究接触表面应力与虚拟材料特征参数的函数关系。

2）本文利用ANSYS 有限元软件, 通过栓接结构静力学分析获得栓接结合部各节点压强值。 通过Matlab 软件, 根据各节点的压强值计算出各节点对应的接触刚度和接触阻尼值, 通过MATRIX27矩阵单元建立栓接结合面节点-节点的接触刚度和接触阻尼单元。 在有限元模型中, 根据栓接结合部非线性虚拟材料不同区域的压强值可以获得对应的非线性虚拟材料参数, 进行栓接结合部结构动力学仿真分析, 获得栓接结合部动态特性。

3）设计L 形组合件进行试验, 验证非线性虚拟材料的可行性。 与传统线性虚拟材料法进行对比可知: 在相同螺栓预紧力的条件下, 非线性虚拟材料固有频率的最大误差为8.80%, 最小误差为2.20%, 结果远远优于传统线性虚拟材料法10%以上的误差, 表明非线性虚拟材料模型可以更准确地表征栓接结合部的动态特性。