浮油组分分离对三浮陀螺仪误差系数变化的机理分析

梁 涛, 王 巍, 李 亮, 孙文利, 凌林本, 沙 立

（1. 北京航天控制仪器研究所, 北京 100039; 2. 中国航天科技集团有限公司, 北京 100048）

0 引言

三浮陀螺仪采用动压气浮支承、液浮支承、磁悬浮定中、高性能铍材、高阻尼氟油等技术,具有精度高、抗过载能力强等优点［1］。 浮子组件利用高密度浮油实现全液浮, 同时利用磁悬浮进行精确定中［2-3］。 浮油是三浮陀螺仪的关键材料之一,主要用来卸载浮子组件的重力。 在陀螺仪工作温度下, 其密度与浮子组件的平均密度相等, 使得浮子组件的重力由浮油产生的浮力平衡, 消除了机械支撑带来的摩擦力矩。

在惯性仪表浮油应用方面, 以美国研制的高精度三浮陀螺仪和三浮陀螺加速度计采用的浮油为代表, 1958 年以前采用全氟油, 后来采用的是高比重、高阻尼的氟溴油、氟氯油、聚三氟乙烯、卤化碳等。 这些浮油的制造及性能鉴定非常严格,要求无尘、无腐蚀、高击穿强度、高介质常数、低介质损耗、低介质吸收。 同时, 为了避免浮油在工作过程中分解、分离, 采用了同一温度下分馏的单馏分浮油。 国内从20 世纪80 年代起就生产液浮陀螺仪所使用的氟油, 包括氟溴醚油、氟溴油和氟氯油。 三浮陀螺仪在研制历史上, 先后使用了氟氯油、氟溴油、氟溴醚油等浮油, 由多种分子量不同的聚合体调和而成, 其化学特性较稳定, 广泛应用于高精度液浮仪表。 但氟油的缺点是生产工序较多、工艺复杂, 其批次间一致性较差, 成本也较高。

在Denhard 所著《惯性元件试验》 一书中, 描述了浮液对液浮陀螺仪精度的影响［4］。 液浮陀螺仪使用的浮油为具有一定聚合度的短链聚合物, 链长和组成成分因聚合工艺参数的变化而不同。 一方面, 长链分子在冷却时, 由于高黏度和体积收缩会对软导线产生损伤, 导致仪表精度发生变化;另一方面, 聚合物会在热对流的过程中分离, 较重的长链分子扩散到较冷的面, 较轻的短链分子扩散到热面, 发生相互对流。 浮油分成密度不同的层, 并在密度梯度正方向产生质量不平衡, 在陀螺仪姿态变化时产生干扰力矩, 引起漂移。

浮油的黏滞干扰力矩对陀螺仪精度有较大影响, 而上述密度分离造成的干扰力矩与陀螺仪温度场息息相关。 流体层中的温度梯度引起流体微团密度变化, 从而受到浮力作用产生对流, 这也是Rayleigh-Benard 对流发生的原理。 针对静压液浮陀螺仪和三浮陀螺仪内部浮油温度场, 采用有限元仿真分析的方法［5-7］得到了陀螺仪内部温度场,并通过试验方法对三浮陀螺仪内部温度场进行了测试, 仪表内部温度场的局部梯度达到0.1℃～0.3℃。 目前, 这一温度梯度无法消除, 该温度梯度仍会导致浮油组分分离, 从而在陀螺姿态变化时产生额外的干扰力矩, 引起漂移。

在使用过程中发现, 陀螺仪在工作状态下的某一位置长时间放置后, 再次标定的一次项误差系数有较大的变化。 经过初步定位, 发现该问题确实为浮油引起, 而且不同类型的浮油、甚至同一类型不同批次的浮油对陀螺仪姿态变化时引起的漂移不同, 但其影响机理需要进一步分析。

本文首先建立了浮油分布态下的温密方程,以此参数对浮油在重力场及温度梯度下进行了组分分离的仿真, 计算了组分分离引起的质量不平衡力矩。 其次, 建立了密度差异对陀螺仪形成的质量不平衡力矩的数学模型。 最后, 通过对姿态变化前后一次项误差系数的测量, 证实了这种密度差异造成的质量不平衡力矩的存在。

1 浮油密度分离仿真计算

利用分子动力学模拟产生的各组分温密方程,采用Fluent 软件对浮油密度分层现象及干扰力矩进行了数值模拟分析, 获得了长时间静置状态下的浮油整体密度分布及组分分布, 并对三浮陀螺仪位置突然转换90°后由浮油密度不均引起的干扰力矩进行了分析与定量计算。

1.1 浮油各组分的温密方程建立

为了研究分子量和温度对氟溴醚油密度的影响, 采用Materials Studio 软件构建了不同分子量的氟溴醚油密度计算模型, 并计算模型在不同温度下的密度。 通过APC 凝胶色谱仪测试氟溴醚油的分子量, 如图1 所示。 峰1、峰2、峰3 对应组分1、组分2、组分3, 分子量测试结果分别为8600、8400、8100, 并对分布峰进行分峰处理, 计算其组分占比, 如表1 所示。

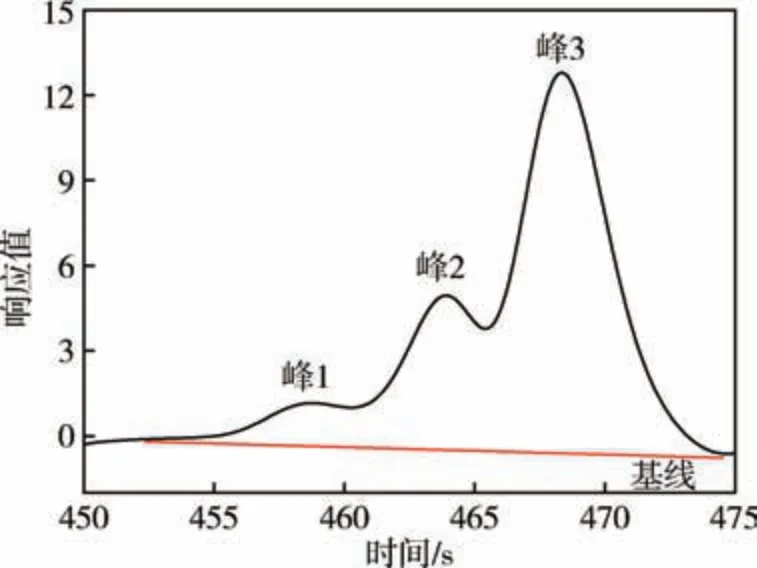
图1 氟溴醚油分子量分布峰Fig.1 Molecular weight distribution peak of fluorobromoether oil

表1 不同氟溴醚油组分的体积占比Table 1 Volume proportion of different fluorobromoether oil components

构建分子量依次为8600、8400、8100 的氟溴醚油组分, 在仿真软件中单位尺寸的立方体盒子中进行填充, 为直观体现温度对单组分氟溴醚油密度的影响, 设置模型的温度分别为58℃、62℃、66℃、70℃, 得到不同分子量在不同温度下的分子动力学密度计算模型。 如图2 所示, 三种分子量的密度与温度均呈现出明显的线性关系, 拟合后得到直线的斜率作为密度随温度的变化率, 即可得到如表2 所示的温密方程。 根据温密方程的斜率变化可以得出, 温度的变化对低分子量氟溴醚油的密度影响更大, 这是由于低分子量氟溴醚油的链长较短, 分子链的卷曲与链间的缠结现象较少,因此运动能力更强, 环境的变化对其自身物化性质的扰动较大。 高分子量氟溴醚油具有更长的链长和更为复杂的微观结构, 因此具备更强的抗温变能力。 对于不同分子量的氟溴醚油, 温度的增加造成密度不同程度的降低。

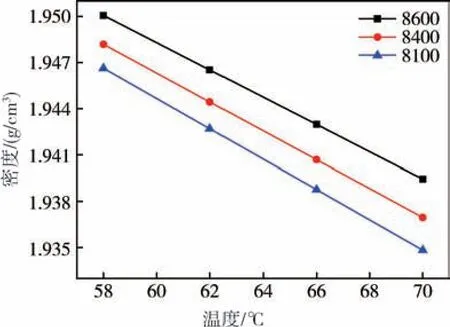
图2 不同氟溴醚油组分的温密方程曲线Fig.2 Temperature-density equation curves of different fluorobromoether oil components

表2 不同氟溴醚油组分的温密方程Table 2 Temperature-density equations of different fluorobromoether oil components

各组分质量与整体质量的关系如下

在一定分子量范围内, 忽略分子间间隙, 假设各组分体积之和即为总体积, 式（1） 两边除以V得

式（2）中,φi（i=1, 2, 3）为氟溴醚油各组分的体积分数。 代入66℃时各组分的密度与体积分数,表3 所示计算结果与实测结果较为一致, 差异仅0.001g/cm3, 说明氟溴醚油各组分的温密方程建立正确。

表3 计算密度与实测密度对比（66℃）Table 3 Comparison between calculated density and measured density（66℃）

1.2 材料属性及边界条件

（1）材料属性

浮油之间的导热系数、比热容、黏度参照氟溴醚油测试的数据, 并认为分子量差距较小时对这三个性能的影响可忽略不计, 各组分物性参数如表4 所示。

表4 不同氟溴醚油组分的物性参数Table 4 Physical parameters of different fluorobromoether oil components

其中,T的单位为摄氏度（℃）, 导热系数与黏度的定义温度为66℃。

（2）边界条件

①内壁面

浮油受到的热量来源主要是浮子内部元件发热, 其发热功率恒定, 内部热源产生的热量首先传递到内壁面上。 在内壁面厚度方向上, 热传导是热量传递的主要方式, 内壁面另一端与浮油接触。 因此在设置边界条件时, 由于内热源发热量恒定, 且材料导热系数可知, 在仿真分析中则设定为恒温壁面。

②重力方向

求解长时间静置状态时, 设定重力方向沿y轴负半轴; 姿态瞬时改变90°时, 通过改变重力方向进行模拟, 设定重力方向沿x轴负半轴。

③初始计算条件

给定浮油、内外壁面初始温度, 对壁面换热系数等进行设定, 同时设置各组分所占比例, 并将各组分均匀分布, 求解类型为稳态。

1.3 静置状态下密度场及温度场分布计算结果与分析

（1）浮油密度分布

计算得到的浮油密度分布如图3 所示。 从整体上可以看出, 浮油内部轻组分上升, 重组分下降,形成了顶部轻组分聚集、底部重组分聚集的现象,因此导致浮油顶部密度小, 底部密度大。 由分析得到, 顶部密度最小处密度为1.938g/cm3, 底部密度最大处密度为1.943g/cm3, 最大密度差为0.005g/cm3, 平均密度差为0.001g/cm3。

（2）扭矩计算

在长时间静置状态下, 浮油发生了轻重组分分离现象, 造成了浮油密度不均, 呈现出底部密度大、顶部密度小的特点。 当陀螺仪状态突然改变时, 这种密度差异会产生一种质量不平衡力矩,造成了陀螺仪精度误差。

在经过静置状态的计算后, 将重力方向沿原平面旋转90°, 通过此方式模拟陀螺仪旋转90°后的情况, 以此计算最大质量不平衡力矩。 计算得到的力矩如表5 所示。

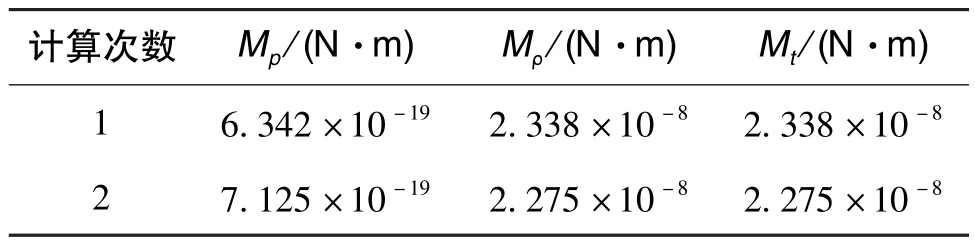
表5 质量不平衡力矩计算值Table 5 Calculated value of mass imbalance torque

表5中,Mp为压力引起的力矩,Mρ为密度差异引起的力矩,Mt为总力矩。

按照三浮陀螺仪角动量H为29mN·m·s 计算, 该综合力矩引起的三浮陀螺仪一次项误差系数变化为0.17（°） /（h·g）。

2 浮油密度分离造成的不平衡力矩数学模型

将浮油看作一个整体, 流体为附着在陀螺仪浮子组件浮筒外壁面上的一个流动整体, 考虑其与三浮陀螺仪浮筒之间的相对流动, 计算此状态时流体在温度场下形成的密度梯度, 计算该梯度引起的对输出轴的干扰力矩。

将液体分成许多微元体, 计算每一微元体对输出轴的干扰力矩, 并通过积分求得合力矩。

首先, 计算在标准柱坐标系下的柱体体积

将密度ρ、重力加速度g代入式（4）中, 考虑每一微元体对输出轴的作用力, 得到

每个微元体的质心为作用力的作用点, 其与输出轴距离为rsinθ, 将该距离代入式（5）并展开得到干扰合力矩计算公式, 求积分并整理（注: 力矩公式M=F·r）

式（6）中,R＜r＜R+δ,R为浮子组件半径,δ为浮子组件与壳体组件之间的间隙; 0 ＜l＜L,L为浮子组件浮筒的长度; 位置转换后, 且认为大密度物质与小密度物质各占一半, 则在三重积分中有0 ＜θ ＜π, 对于项, 计算得

因为δ与R相比为小量, 则忽略带有δ2与δ3的高次项, 保留δ的一次项, 则化简后得到

将式（8）代入式（6） 中, 并继续求解三重积分,得到

该力矩为0≤θ≤π 范围内力矩, 当浮油在温度梯度下, 在重力的作用下在垂直方向形成密度梯度后, 下层和上层的平均密度为ρ1、ρ2（ρ1＞ρ2）,则当三浮陀螺仪发生转位如图4 所示时, 三浮陀螺仪浮子组件圆周方向形成的质量不平衡力矩为

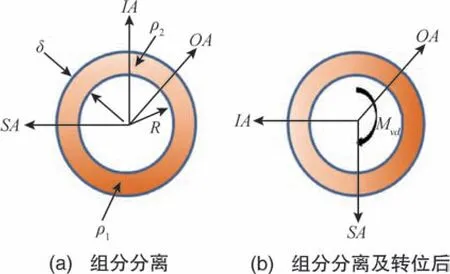
图4 浮油组分分离及分离后形成的质量不平衡力矩Fig.4 Schematic diagram of oil components separation and mass imbalance torque formed after separation

式（10）中,Mvd为浮油密度分离引起的输出轴上的质量不平衡力矩,ρ1为浮油分离形成的较大平均密度,ρ2为浮油分离形成的较小平均密度。

三浮陀螺仪浮子组件半径R取22.5mm, 浮子组件与壳体组件之间的间隙δ取0.1mm, 浮子组件浮筒的长度L取42mm, 分离后的密度ρ1、ρ2未知, 若按照0.001g/cm3的密度差计算, 其引起一次项常值变化为0.28（°） /（h·g）, 该数值在量级上与仿真结果相近。

3 浮油对陀螺仪姿态变化下的精度测试

三浮陀螺仪输入轴相对于惯性空间的总漂移为

式（11） 中, 忽略二次项,ωe为地球自转角速度沿陀螺输入轴的分量,Df、Di、Ds、Do为漂移系数。Df大小与重力加速度无关, 称为零次项;Di、Ds、Do与重力加速度一次方相关, 称为一次项,一般采用六个位置力反馈法进行陀螺仪误差系数的分离标定。

初始状态下, 将三浮陀螺仪在位置3 放置。 陀螺仪在自身温度梯度、重力场影响下, 如图5 所示, 在位置3 的IA轴负向形成了较高密度层。 当陀螺仪转至位置4 或位置6 进行误差系数标定时,就引入了OA轴上的质量不平衡力矩。

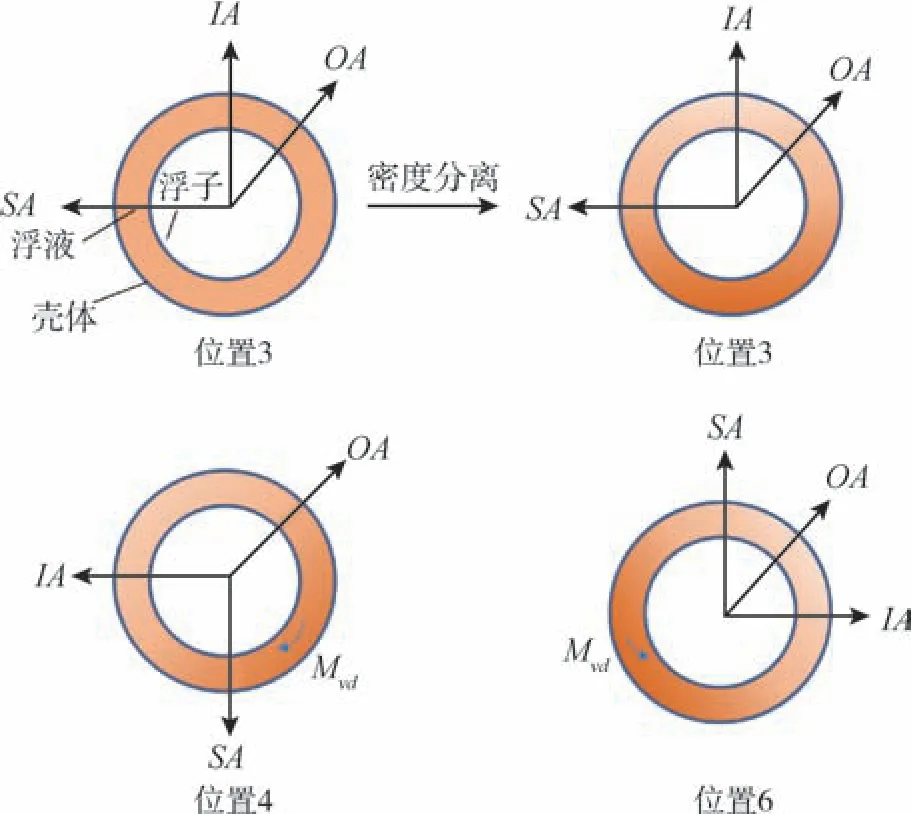
图5 浮油密度分离导致姿态变化后输出轴形成的力矩Fig.5 Viscous torque of OA-axis caused by oil density separation after attitude change

在多位置误差系数静态测试标定时, 有

式（12） ～式（14）中,wI4、wI6分别为位置4、位置6 下的陀螺仪漂移系数;KT为陀螺仪标定因数;I为力矩器电流;Df为与重力加速度不相关干扰力矩引起的误差系数;为IA轴上与加速度一次项相关的质量不平衡量;Ds为测试求解到的与重力加速度一次项相关的误差系数;为由于浮液密度分离引起的OA轴上的质量不平衡力矩, 并假设在多位置误差系数标定时, 这部分力矩在多位置下是相等的。

当三浮陀螺仪在图5 位置3 停留较长时间后,需重新开始误差系数标定。 陀螺仪在位置4 测试时, 在OA轴上的质量不平衡力矩为正力矩; 在位置6 测试时, 在OA轴上的质量不平衡力矩为负力矩, 通过式（12） ～式（14）可计算出求解到的与重力加速度一次项相关的误差系数Ds。 所以就体现出图6 中Ds在位置3 放置后向负向变化的趋势, 而测试前后的变化值约为0.25（°） /（h·g）, 这与数学模型中0.001g/cm3密度差异的计算结果十分接近,也说明了数学模型的正确性。

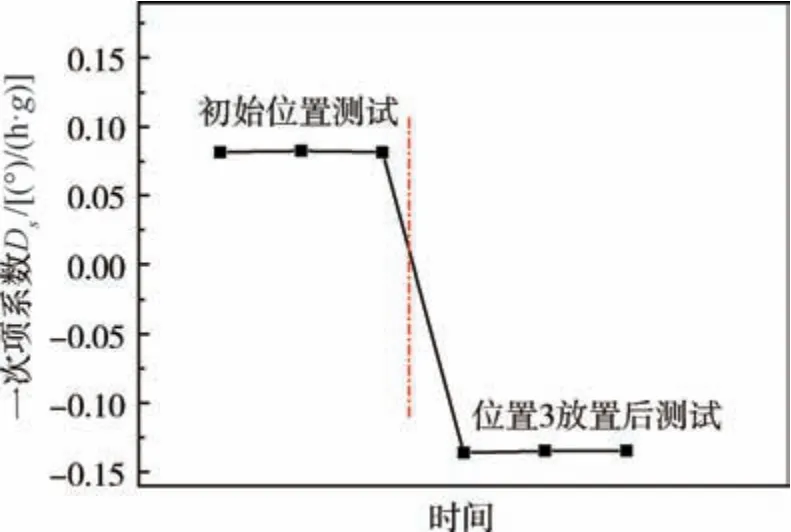
图6 陀螺仪姿态变化下一次项系数Ds 的变化Fig.6 Ds changes of gyroscope after attitude change

4 结论

本文通过建立陀螺仪浮油分布态下的温密方程, 以此参数对浮油进行了组分分离的仿真, 并计算了组分分离引起的质量不平衡力矩。 提出了一个数学模型求解该质量不平衡力矩, 并通过了陀螺仪一次项误差系数分离测试。 测试分离的该力矩, 三者数值均在一个数量级上, 互相证明了这种密度差异造成的质量不平衡力矩的存在, 该结论对后续研究高精度惯性仪表用浮油指标特别是分子量分布特性具有一定的意义。