求解抛体运动的极值问题

聂应才 杨小毓

(江西省南丰县第一中学)

抛体运动是以一定速度将物体抛出且物体在运动过程中受到恒力作用的运动。它是典型的曲线运动,体现了“化曲为直”的物理思想,运动规律是学习的重点,其极值问题是运动学的难点,它综合了运动合成与分解法、数学处理法等,考查了科学推理论证的科学思维。

1 速度的极值

抛体运动一般以抛出点为坐标原点O、沿恒力方向为y轴、与恒力垂直方向为x轴建立直角坐标,x轴方向做匀速直线运动,y轴方向做匀变速直线运动。联立x轴、y轴运动规律解决速度极值问题。

【例1】一带有乒乓球发射机的乒乓球台如图1所示,水平台面的长和宽分别为s1和s2,中间球网高度为h。发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为2h。不计空气的作用,重力加速度大小为g。若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )

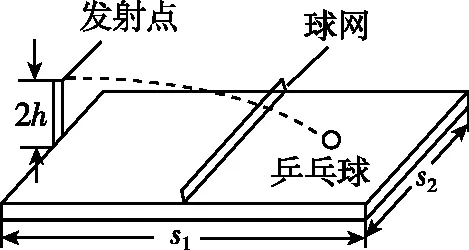
图1

【答案】B

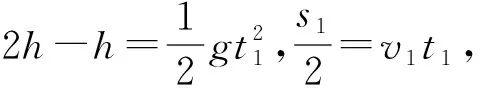
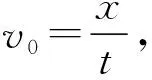
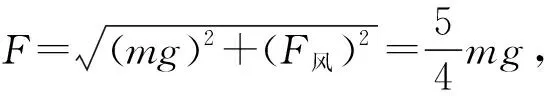
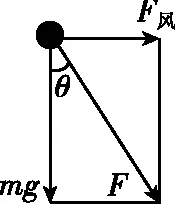
图2

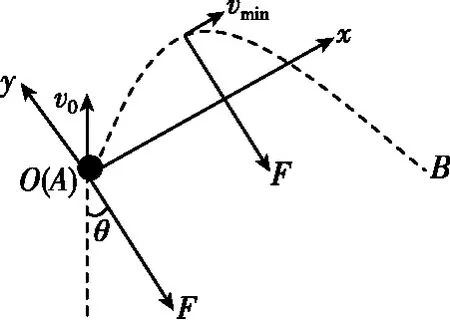
图3

【点评】小球速度最小处,合力F与速度vmin垂直,之前合力F与速度v夹角为钝角,速度减小,之后合力F与速度v夹角为锐角,速度增大。

2 位移的极值

根据抛体运动规律,列出位移表达式,结合数学知识解决位移极值问题。

【例2】某科技比赛中,参赛者设计了一个轨道模型,如图4所示。模型放到0.8 m高的水平桌子上,最高点距离水平地面2 m,右端出口水平且高度可调。现让小球在最高点由静止释放,忽略阻力作用,则小球飞得最远水平距离x是多少?

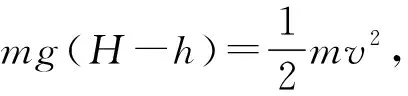
【点评】右端出口调低可获得较大的平抛初速度v,但平抛时间t变短,反之右端出口调高平抛初速度v较小,平抛时间t变长,水平距离x不是右端出口高或低就大,而是要写出水平距离x与右端出口高度h的函数关系,由数学知识求得当h为某值时,x最大。

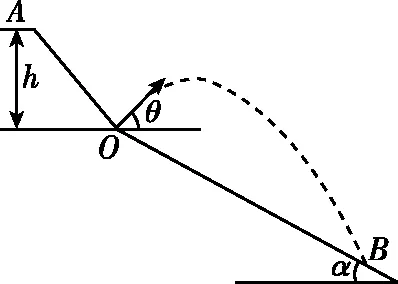
图5

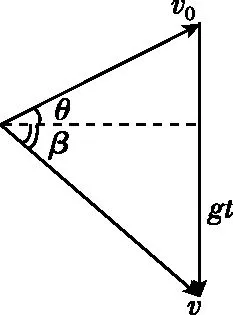
图6

3 时间的极值

抛体运动的分解不是唯一的,在斜面上实验,把它分解为沿着斜面和垂直斜面这两方向的直线运动,能快捷解决问题。

【例3】如图7,倾角为37°的斜面足够长,从斜面上b点正上方2.5 m处的a点,以2 m/s的速率抛出一个小球,方向不定,且小球的轨迹与abO在同一竖直平面内,则小球落回斜面的最长时间为(g取10 m/s2,sin37°=0.6)( )

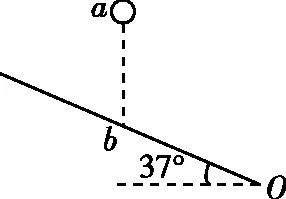
图7

A.0.5 s B.1 s C.1.5 s D.2 s

【答案】B

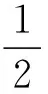
【训练3】例3中球落回斜面的最短时间为( )

A.0.5 s B.1 s C.1.5 s D.2 s

【答案】A

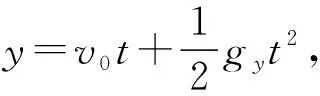
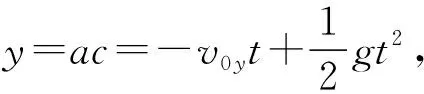
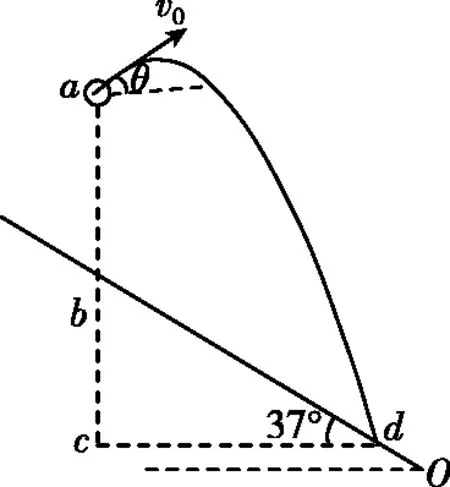
图8

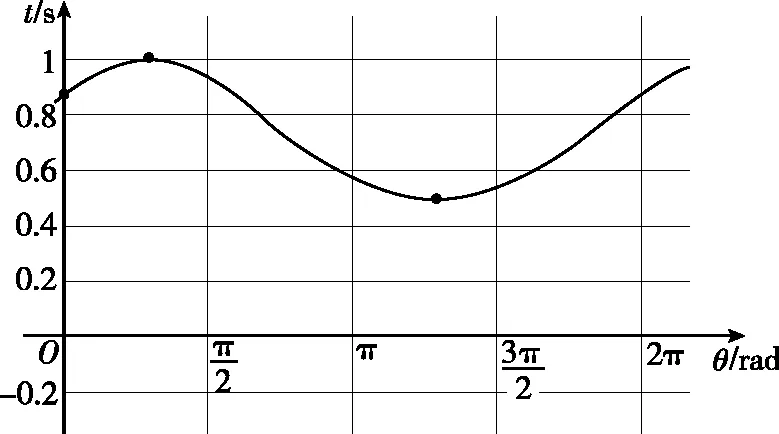
图9

4 动能的极值

物体做抛体运动时,动能会发生变化,根据动能定义,动能的极值实质是速度的极值,可有时需要用动能定理来推理判断。

【例4】光滑水平面上有一个以O为圆心,半径为R的圆,AB为圆的直径,如图10所示,质量为m的小球进入圆内会受到一个平行于圆面的恒力F。小球自A点先后以不同的速度进入圆内,速度方向与恒力F的方向垂直。已知刚进入圆内时速度为零的小球,自圆周上的C点以速率v0穿出圆区域,AC与AB的夹角θ=60°。

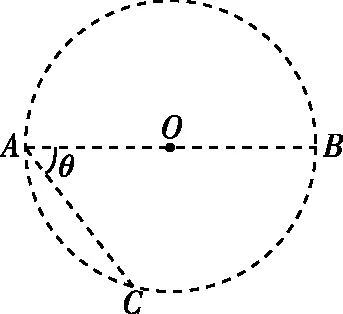
图10

(1)求恒力F;

(2)为使小球穿过圆区域后的动能增量最大,该小球进入圆内时的速度应为多大?

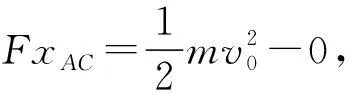
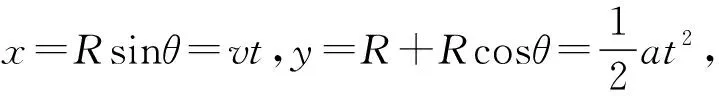
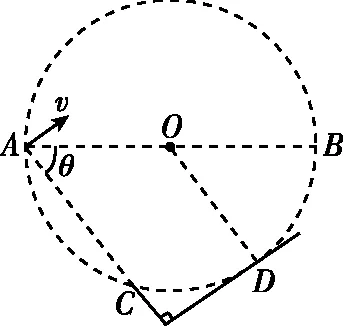
图11

【训练4】如图12所示,AB是竖直平面内半径为R的圆上水平方向的直径。质量为m的小球进入圆内会受到一个平行于圆面的恒力F,其大小等于重力大小mg,g为重力加速度。当小球从A点以相同的初速度v0抛出,抛出方向不同时,小球会经过圆上不同的点,在这所有点中,到达C点时小球的动能最大。已知∠CAB=30°,求:

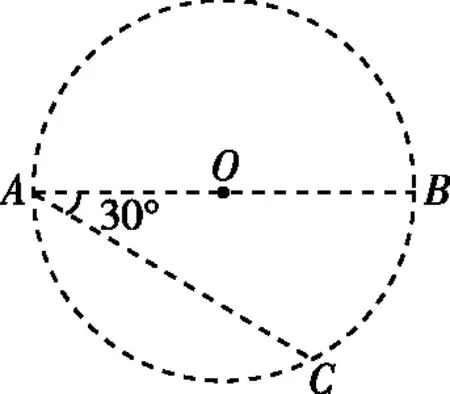
图12

(1)恒力F的方向;

(2)小球在C点时的动能EkC;

(3)小球在B点时的动能EkB。

【解析】(1)小球在圆内受到重力mg和恒力F两个力,要使小球从A点以相同的初速度v0抛出,到达C点时小球的动能最大,小球的合力F合做功最多,C点就是合力F合方向与圆相交的最远的点,则F合方向就是由O指向C,根据平行四边形定则和几何关系,可知恒力F的方向是由A指向C。

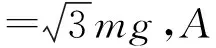
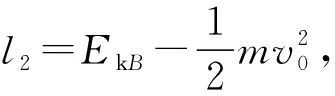
【点评】物体做抛体运动,求解动能极值时,应该优先运用动能定理,把求动能的极值问题转换成做功的极值问题,可以不必考虑抛体运动轨迹,使问题得以顺利解决。

高三复习要整合物理观念,抛体运动不能仅停留在只有重力作用下的运动,提炼出本质的恒力作用,更有正迁移性,如带电粒子在匀强电场下的抛体运动;不能只是运动与相互作用分析思路,还可以用能量动量观看待抛体运动。以问题链方式培育学生的核心素养,发展学生的思维品质。抛体运动的分解不能仅是沿力方向和垂直力方向这两个方向的分运动,有时还要灵活分解。加强应用数学知识处理物理问题的意识和能力,善于运用二次函数、均式不等式、三角函数等数学知识解决物理中的极值问题。