基于主成分分析和聚类分析的不同地区农产品产量研究

焦登丹 王 兰 何远霞

（作者单位：贵州财经大学）

中国作为全球十大农业大国之一，农产品种类繁多且数量庞大。农产品是指来源于种植业、林业、畜牧业和渔业等的初级产品[1]。农产品可以加工成各种各样的食物，为人们提供碳水化合物、蛋白质等基本营养物质和能量。因此，本文对我国31 个省（自治区、直辖市）的农产品进行主成分分析和聚类分析，以使读者了解各地区农产品产量分布情况和不同农产品的产量差异。

一、主成分分析与聚类分析方法介绍

（一）主成分分析思想

主成分分析（Principal Component Analysis，PCA）[2]是一种线性降维的方法，当变量之间存在相关性时，将多个原始变量转化为一个或几个综合指标，这些综合指标叫作主成分。每个主成分都是原始变量的线性组合。设样本资料矩阵X=(x1,x2,…,xp)T是由容量为n的p维向量构成的矩阵，其协方差阵为∑，λ1,λ2,…,λp为协方差阵∑的p个特征值，e1,e2,…,ep为特征值λi对应的单位正交矩阵的特征向量，矩阵X的第i个主成分为yi=eiTX，指标称为方差贡献率，用来度量每个主成分包含原有信息的多少。

（二）聚类分析方法

聚类分析是一种利用某种度量方式来度量样品间亲疏关系的方法，将关系较近的样品聚为一类，而关系较远的聚为另一类[3]。本文采用系统聚类法进行聚类分析，具体步骤如下。

设样本资料矩阵是由容量为n的p维向量构成。首先，选择样品之间和类别之间距离的度量方式，本文使用欧式距离，见式（1）。将n个样本点看作n类，即每个类中只包含一个样品，此时计算类与类之间的距离。设定一个阈值T，若对i∀i,j∈G,i≠j，均有dij＜T，则称G对于阈值T构成一个新类，并计算这个新类与其他类的距离dij，若满足dij＜T，则继续合并成另一个新类。不断重复这样的操作，直到所有样品合并成一个大类。

二、实证分析

本文所使用的所有数据均来自《中国统计年鉴》。选取2020 年我国31 个省（自治区、直辖市）的农产品产量，共9 个相关指标，分别是肉类产量（x1）、水产品总产量（x2）、水果产量（x3）、家禽出栏量（x4）、木材产量（x5）、粮食产量（x6）、蔬菜产量（x7）、油料产量（x8）、棉花产量（x9）。其中，木材产量和棉花产量的部分数据缺失，使用均值对缺失数据进行填充。

（一）各地区农产品产量的主成分分析

使用SPSS 软件对数据进行主成分分析之后得出如表1 和表2 的结果。

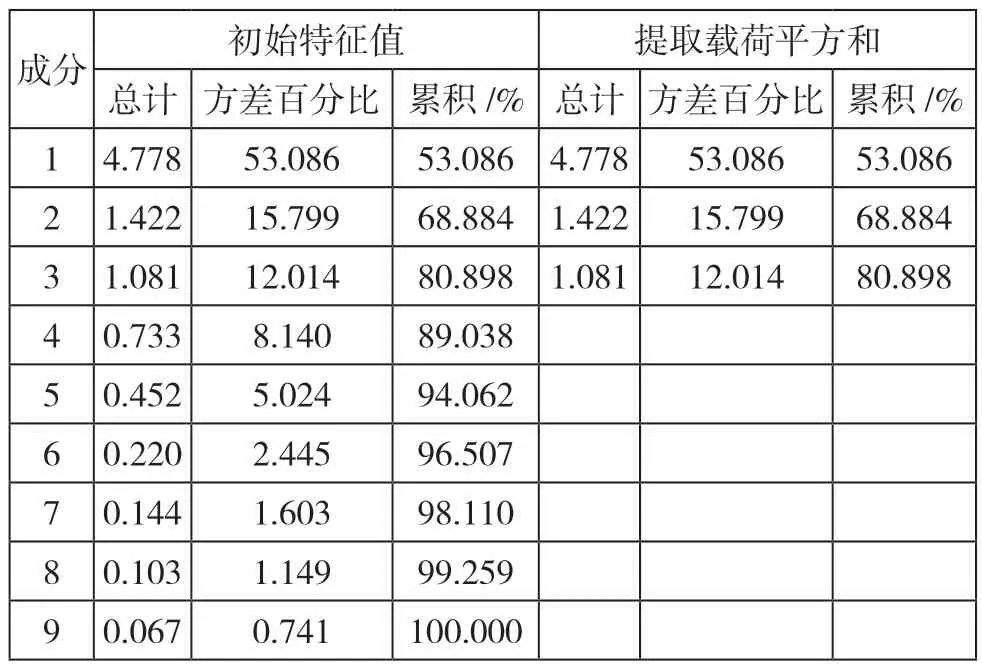
表1 总方差解释

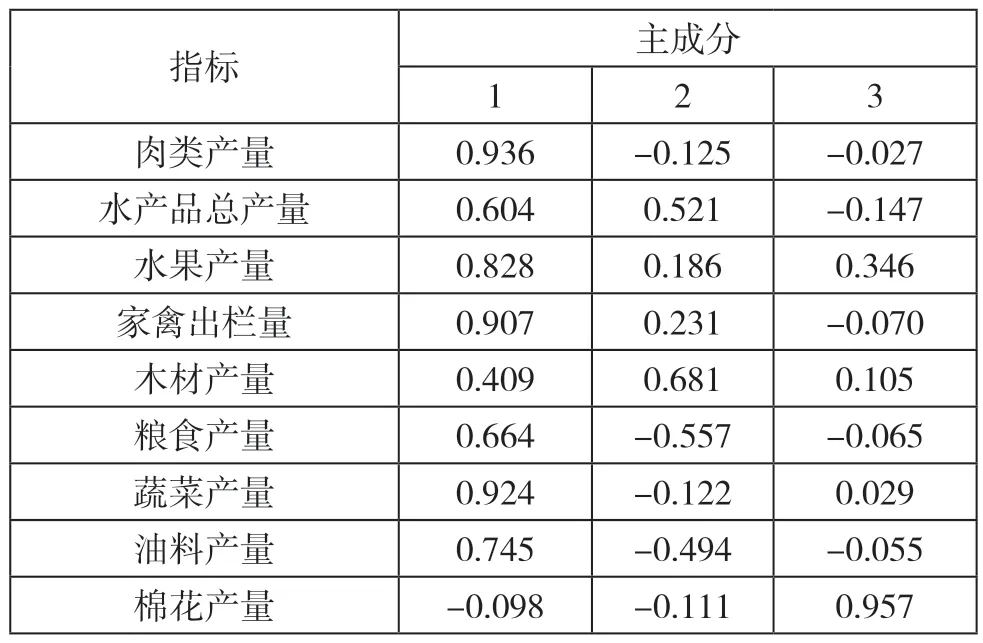
表2 初始因子载荷矩阵

按照特征值大于1 的原则，可以选择前3 个主成分。这3 个主成分的累计贡献率是80.898%，可以反映原变量80.898%的方差，说明效果良好。

从表2 可以看出，蔬菜产量、粮食产量和油料产量等指标在第一主成分（PCA1）中的载荷较大，该主成分主要反映了主食的产量情况；水产品产量、木材产量指标在第二主成分（PCA2）中的载荷较大，反映了木材产量和水产品产量信息；第三主成分（PCA3）主要反映棉花产量信息。

选定主成分yi之后，根据表1 和表2 进一步写出各主成分方程：

式（2）中，ωij表示各主成分载荷，θj是表2 中各变量对应的系数，λi是表1 中各主成分对应的特征值。

将求得的主成分载荷带入主成分方程，可得出：

方差百分比表示各主成分提取原始信息的多少，因此综合得分表达式为

将数据进行标准处理后代入式（2）可以得出各主成分得分，见式（7）。将各个主成分得分代入式（6）可得出综合得分。主成分综合得分情况如表3 所示。

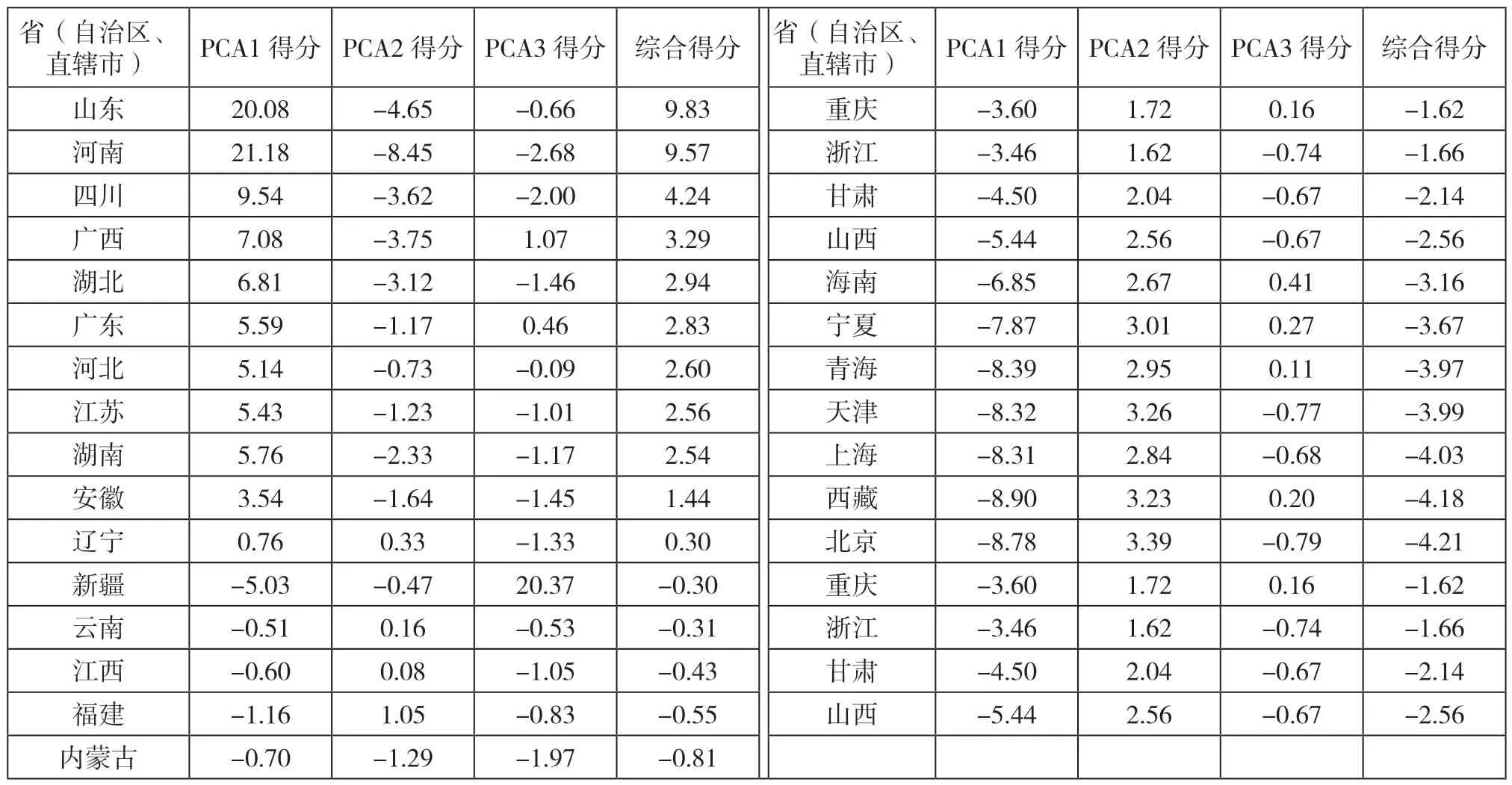
表3 主成分得分情况

由表3 可知，山东省的综合得分最高，说明山东省的农产品产量总和最多；PCA1 得分也最高，说明山东省的蔬菜产量和油料产量较高。这主要是因为山东省土壤肥沃、雨水充足，农业机械化[4]程度较高。河南省各项得分与山东省类似，说明这两个地区农产品产量分布情况相似。天津市、西藏自治区和北京市的PCA1 得分很高，说明这3 个地区各项产量分布相对均衡。新疆维吾尔自治区的PCA3 远高于其他地区，说明该地的棉花产量远高于其他地区。

（二）各地区农产品产量的聚类分析

经过主成分分析降维后，本文选择系统聚类法对31 个省（自治区、直辖市）的3 个综合指标进行聚类分析，采用欧氏距离[5]度量类间距，使用SPSS 软件建立如图1 所示的谱系图，从树状图能看出类与类之间的距离大小。

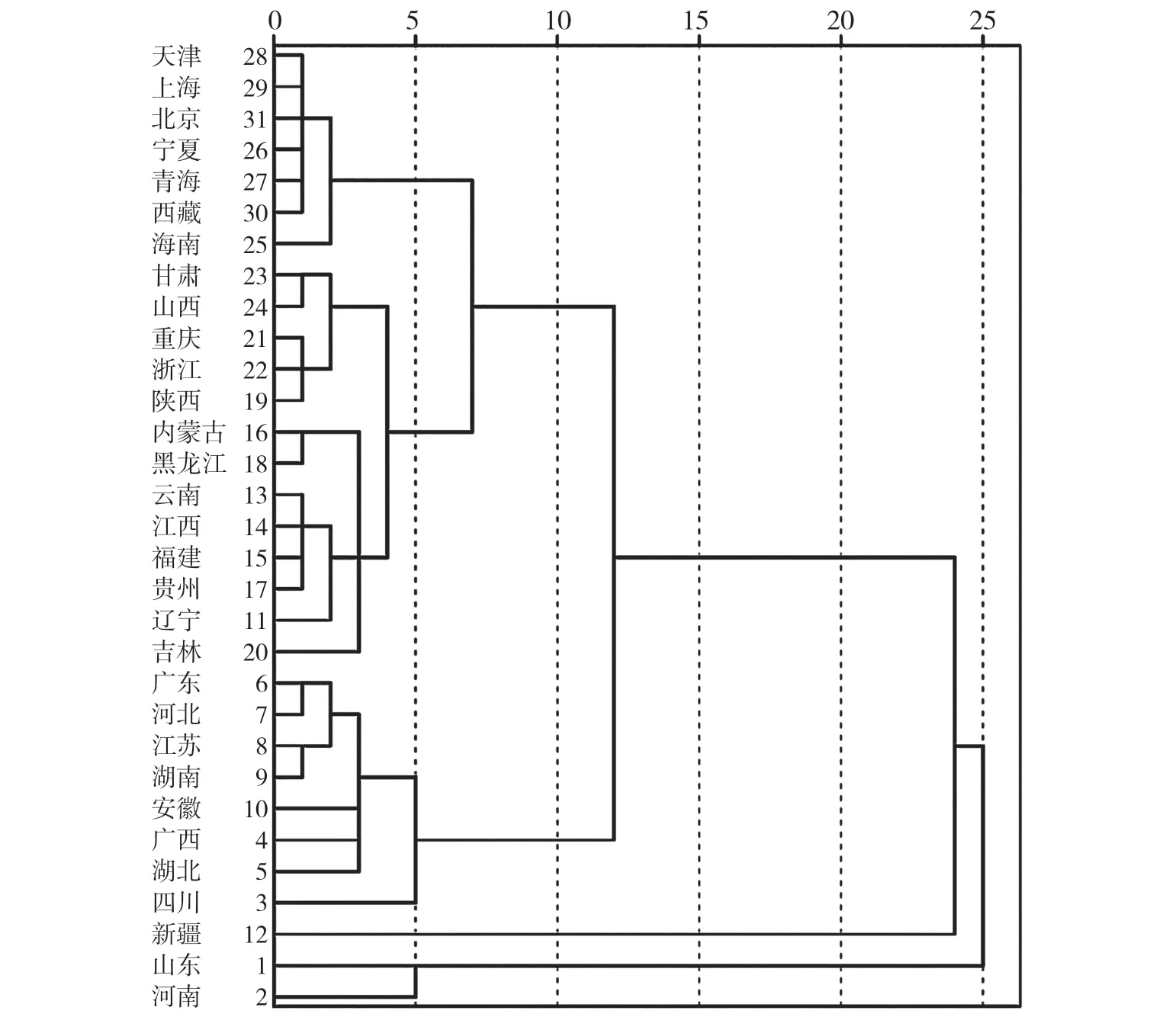
图1 谱系图

根据图1 可将31 个地区的农产品产量划分为4 个大类：第Ⅰ类包含20 个省（自治区、直辖市）：天津、上海、北京、宁夏、青海、西藏、海南、甘肃、山西、重庆、浙江、陕西、内蒙古、黑龙江、云南、江西、福建、贵州、辽宁、吉林；第Ⅱ有8 个省（自治区）：广东、河北、江苏、湖南、安徽、广西、湖北和四川；第Ⅲ类仅有山东省和河南省；第Ⅳ类更少，新疆自成一类。结合主成分综合得分可知，第Ⅲ类是农产品产量最大的两个省份，然后是产量较大的第Ⅱ类，最后是产量较少的第Ⅰ类，新疆自成一类很显然是因为棉花产量大。

三、结语

从整体上看，全国各地农产品产量差异较大，山东省和河南省因农产品产量综合得分远高于其他地区而被分到一类，而新疆棉花产量较大，单独成类。即使综合得分接近的地区，各主成分的得分也存在差异。鉴于我国农产品产量分布不均的现状，建议相关部门能合理分配资源。