探析内在逻辑 强化关键能力
——一道高考压轴题的多视角探析与背景探源
巨小鹏
(陕西省汉中市龙岗学校)
《中国高考评价体系说明》将关键能力作为整个“四层”考查内容的重心,是推进新时代高考内容改革的必然选择,也是教育测量学的规律性要求.2022年全国甲卷理科第21题以考查基础概念和基本解题技能为核心,考查关键能力,以极值点偏移问题为核心问题,极具创新性,问题情境较往年的此类题型更加复杂,更具有综合性,考查了导数在函数中的应用,体现了“四翼”的要求、高考命题以“能力立意”的命题理念以及稳中求新的特点,有利于对学生思维品质和关键能力的考查.
1.试题呈现
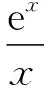
(Ⅰ)若f(x)≥0,求a的取值范围;
(Ⅱ)证明:若f(x)有两个零点x1,x2,则x1x2<1.
2.试题分析与解答
解析:由题意知f(x)的定义域为(0,+∞).
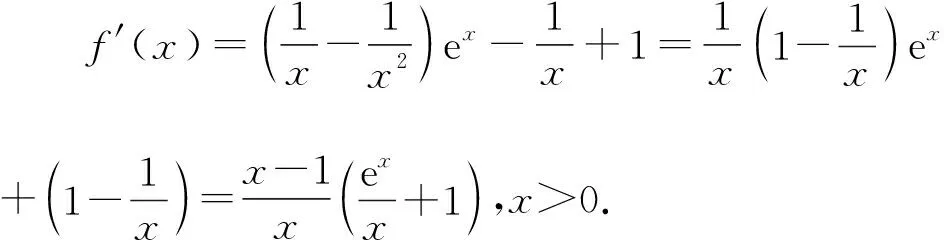

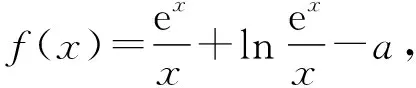
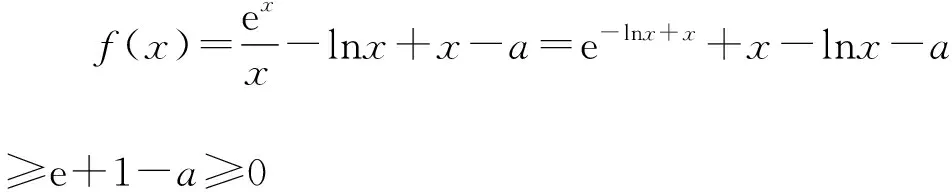

解法6(必要性探路视角):
必要性:f(x)的定义域为(0,+∞),要使f(x)≥0,则满足f(1)≥0,即e+1-a≥0,则a≤e+1.
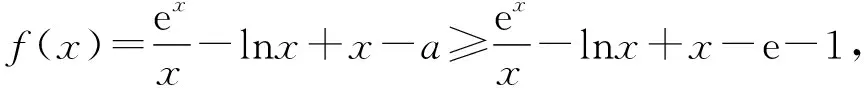
综上所述,a的取值范围为(-∞,e+1].



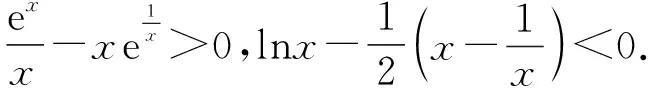




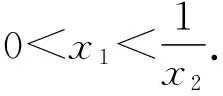
证法4(同构+构造函数视角2):根据证法3可得x1-lnx1=x2-lnx2,由题可设0
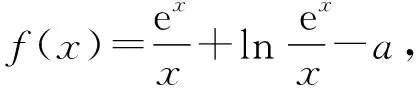



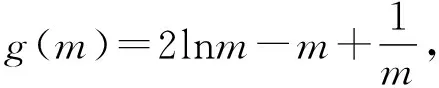


评注:本题是极值点偏移问题,其本质是函数值变化快慢的问题,利用导数研究函数问题.关键点是通过分析、构造函数解决问题.证法1和证法2直接构造函数;证法3和证法4利用同构化繁为简,继续构造使得计算量和思维量大大降低;证法5和证法6借助对数均值不等式使得问题更容易解决;证法7和证法8通过比值和差值换元解决问题.求解极值点偏移问题常用的思考方向是构造对称函数、比值换元、差值换元和利用对数均值不等式解决问题.渗透数形结合、分类讨论和函数与方程的思想,考查学生关键能力和综合核心素养.
3.试题背景探源
3.1 竞赛背景
云散月明谁点缀,天容海色本澄清.近几年高考试题特别是压轴题以竞赛试题为背景,将竞赛题逐渐分解分步,使得试题难度下降,考查学生关键能力.此类竞赛试题很多,选题两个如下:

(Ⅰ)当m=-2时,求函数f(x)的所有零点;
(Ⅱ)若f(x)有两个极值点x1,x2(x1
(答案:(Ⅰ)x=1;(Ⅱ)证明略.)
例2.(2018·全国高中数学联赛福建省预赛)已知f(x)=ex-mx.
(Ⅰ)当x>0时,不等式(x-2)f(x)+mx2+2>0恒成立,求实数m的取值范围;
(Ⅱ)若x1,x2是函数f(x)的两个零点,求证:x1+x2>2.
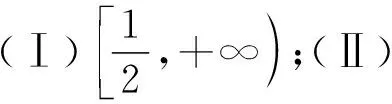
3.2 高考背景
极值点偏移问题常考常新,最早追溯到2009年辽宁卷,2010年天津卷,2016年首次在全国卷中出现,直到2022年考查角度依然新奇,题干创新,情境更加综合,此类往年高考试题选题两个如下:
例3.(2021·全国新高考Ⅰ卷·22)已知函数f(x)=x(1-lnx).
(Ⅰ)讨论f(x)的单调性;

(答案:(Ⅰ)f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞);(Ⅱ)证明略.)
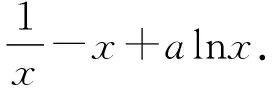
(Ⅰ)讨论f(x)的单调性;
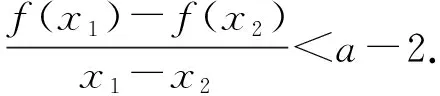
基金项目:陕西省教育科学“十四五”规划2021年度课题:“教材‘阅读材料’在数学学习中的渗透与引领策略研究”(项目编号:SGH21Y1194)

