镁/铝爆炸焊接的数值模拟

赵 宇，缪广红，孙志皓，马秋月，刘自伟

(1. 安徽理工大学 土木建筑学院，安徽 淮南 232001；2. 安徽理工大学 力学与光电物理学院，安徽 淮南 232001)

爆炸焊接是利用炸药的爆轰作用，在普通金属表面覆上一层具有特殊性能的优质金属，制成双层的金属材料，具有更良好的物理化学性质，避免全部使用优质材料带来的浪费。通常的制作双层多层复合材料的方法有焊接法、轧制法等。这些方法在面对各种金属材料时有很大的局限性，如生产复合产品效率低，生产成本较高等。爆炸焊接相当于一种新的途径适用于广泛的材料组合：熔点差距较大（铅/钽）；硬度差距较大（铅/钢）；热膨胀系数差距较大（钛/304 不锈钢）等。爆炸焊接有更大的复合比选择，对于材料的大小、形状、尺寸限制较小[1]。爆炸焊接的复合板质量较好，有很好的再加工条件。爆炸焊接工艺简单，价格低廉，潜力很大，现已成为金属加工领域的重要方法。为便于观察爆炸焊接过程，Oberg 等[2]最先采用数值模拟来分析爆炸焊接的过程，取得较好的效果，后各国学者纷纷采用数值模拟，对爆炸焊接过程的波形、射流等进行模拟。

王呼和等[3]通过ANSYS/LS-DYNA 软件对爆炸焊接过程波形的形成进行数值模拟，模拟结果与实验高度一致。王宇新等[4]应用MPM 法计算三维爆炸焊接问题，在爆轰载荷作用下的飞板和基板的金属动态变形过程进行了三维数值模拟，并且对飞板的碰撞点速度和爆轰压力变化进行了计算分析。太原理工大学袁晓丹[5]采用ANSYS 有限元对铝合金/镁合金进行模拟，观察了材料运动状态以及界面的结合机制；张婷婷[6]采用数值模拟观察出铝/镁合金界面的特征连接机制。王梦茵[7]用SPH 方法对双金属爆炸焊接进行模拟，观测界面波形。SPH 是以粒子代替网格，采用Lagrange算法，让粒子具有材料的力学性质，且精度较高，在爆炸焊接领域具有很好发展潜力。本文借助ANSYS/LS-DYNA 软件，采用SPH-FEM 耦合算法，对铝/镁合金爆炸焊接进行数值模拟。

1 建立爆炸焊接窗口

临界碰撞角度、临界冲击压力、最大冲击速度和临界流体传输速度4 个变量放在同一坐标内，就可以建立爆炸焊接窗口，在焊接窗口内部，才能获得良好的爆炸焊接复合材料。平行法爆炸焊接中，任选2 个变量即可建立爆炸焊接窗口，如图1，以碰撞点速度与复板碰撞速度建立窗口。

图1 爆炸焊接窗口

1.1 流动限（vc, min）

为保证金属板在高速碰撞时产生射流，撞击点所满足的最小速度vc,min。当复板碰撞时，如果撞击点的移动速度小于vc,min，碰撞区的压力小于材料的动屈服强度，无法产生射流现象，焊接失败[8]。撞击点最下移动速度可由Ezra 公式[9]确定：

式中：vc,min是临界碰撞速度，cm/s；σ 是2个材料中较高的屈服强度，MPa；ρ为2 个材料中密度较小值，g/cm3；

表1 实验参数

根据表内参数计算出vc,min=1 447 m/s。由文献[10]在平行法爆炸焊接时，碰撞点的速度等于炸药的速度，即炸药爆速需要大于1 447 m/s。对应图中边界ad。

1.2 声速限（vc, max）

进行异种金属焊接时，为确保界面出现射流现象，撞击点的移动速度要小于金属材料较小的体积声速c[11]。

求得vc,max=4 516 m/s，对应图中边界bc。

1.3 下限（vp, min）

要想成功焊接镁/ 铝合金复合板，爆炸焊接界面必须产生射流和较大的塑性变形。这就需要复板要以足够大的速度与基板发生碰撞，产生足够大的压力，以保证焊接成功。这个焊接成功的最小临界速度，即为焊接下限，可由以下公式求得[11]：

式中：σb——材料的抗拉强度，Pa；

ρ——材料的密度，kg/m3。

由于进行的异金属镁/铝合金爆炸焊接，则vp,min需要其强度最高的金属材料发生塑性变形，此最小速度可通过下面步骤计算：

（1）分别计算出铝镁合金产生射流所需的vp,min。

（2）计算该速度vp,min下的碰撞压力即：

式中：ρ——密度，kg/m3；

up——最小碰撞速度，m/s；

c——体积声速，m/s。

（3）由式（4）计算出镁铝的压力为pmin1和pmin2。

（4）要想使2 种材料都发生射流，就需要以最大的碰撞压力，代入（4）重新计算最小碰撞速度，此碰撞速度与较大压力的临界速度之和，即为焊接所需最小临界速度vp,min。

按照上面步骤计算得vp,min=411.4 m/s。因此，复板的碰撞速度必须大于411.4 m/s。

1.4 上限（vp, max）

为了防止焊接过程动能损失较大，导致界面出现熔融层等现象，需要对镁铝板最大碰撞速度vp,max做出限制，可用以下经验公式[12]求出：

式中：N——实验测得常数，通常取0.11；Cp——复板比热容；J/（kg·K）；C0——材料声速，m/s；k——热导率，W/（m·K）；ρ——复板材料密度，g/cm3；h——复板厚度，25 mm；Tm——熔化温度，K。

将参数带入可得vp,max=548 m/s，可得爆炸焊接窗口的ab 边界。

2 模型与材料参数

2.1 模型

根据长安大学唐亮亮[13]的以实验模型，复板为5052 铝合金，基板为AZ31B 镁合金，利用LS-DYNA 建立如图2 模型，为减弱边界效应带来的影响，炸药尺寸为31 cm×32 cm×2.5 cm/2.0 cm/1.8 cm，复板尺寸为31 cm×32 cm×0.5 cm，基板尺寸为30 cm×30 cm×1.3 cm，基复板间隙为0.5 cm/0.3 cm。炸药进行SPH 粒子化处理，基复板均采用拉格朗日网格划分，采用膨化硝铵炸药，密度为0.68 g/cm3，爆速为2 100 m/s，边部中心起爆方式。考虑到模型具有对称性，为提高计算效率，选取1/2 模型进行计算，单位制cm-g-µs。

图2 计算模型

2.2 模拟的参数选择

LS-DYNA 软件对炸药选用高能燃烧模型，JWL 状态方程的表达式[14]为：

式中：V——相对体积，E0——初始能密度，A、B、R1、R2、ω——实验测得参数。

炸药的具体JWL 状态参数见表2。

表2 硝铵炸药JWL 状态参数

数值计算中，金属板均采用Mie-Gruneisen 状态方程和Johnson-Cook 材料模型[14]。Johnson-Cook材料模型和Mie-Gruneisen状态方程的参数见表3。

表3 Johnson-Cook 材料模型和Gruneisen 状态方程参数

3 模拟结果与分析

在三维模拟计算中，分别设置下表4 所示爆炸焊接参数建立模型。采用Deribas 提出的公式计算出复板碰撞速度vp，以及文献[15]给出的理论公式计算出碰撞角。

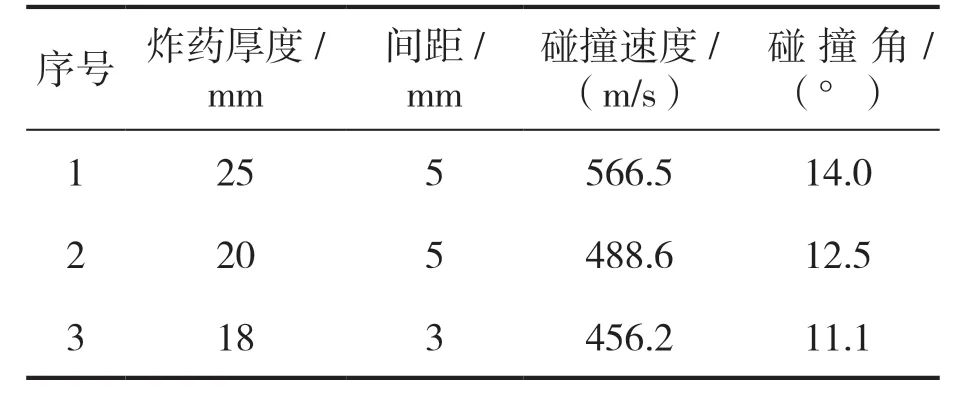
表4 爆炸焊接参数和理论计算结果

3.1 不同焊接参数下复板位移

在三维模拟中，材料参数各项不变，得到如图3 所示位移-时间曲线。由图3（b）、（c）、（d）可知，在复板上分别选取的A、B、C、D 四个单元，均大于基复板间距，证明焊接质量较好。关于位移大于间距，文献[13]认为，复板位移大于间距，可能是因为基复板在碰撞时，在界面发生互相渗透，也存在界面发生融化现象。此外，由爆炸焊接模拟过程可以看出，基复板都有一定程度的压缩变形，致使爆炸焊接过程中有一定的减薄率。

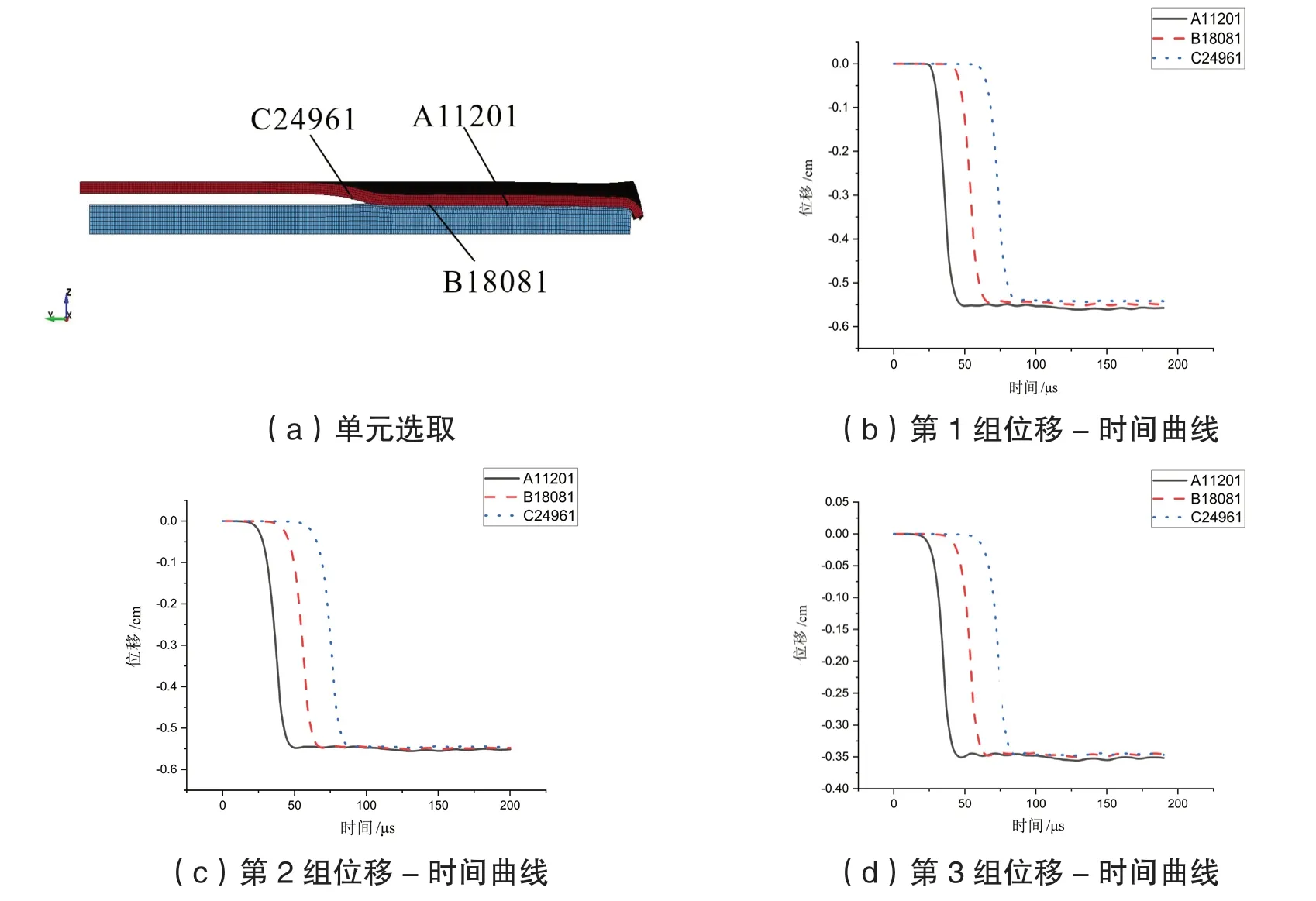
图3 不同参数下位移-时间曲线

3.2 复板的碰撞速度及压力分布

在3 组模拟中，选取复板上同一单元13281，分别绘制速度-时间曲线（a），压力-时间曲线（b）。模拟速度与理论计算对比结果见表5。

表5 速度模拟与理论计算

由速度-时间图4（a）可知，3 组复板的碰撞速度均在爆炸焊接窗口内部，548 m/s ＞411.4 m/s，证明焊接质量较好。由1、2 组数据可知，炸药复板质量比对碰撞速度有较大的影响，如图4，一定范围内质量比越大，复板撞击的能量越大[16]，碰撞速度越大，碰撞压力也越大。碰撞能量与碰撞速度关系由公式（8）[17]确定：

图4 复板碰撞速度和压力分布与时间关系曲线

式中：E 为碰撞能量、mf、mb分别为复板、vp基板的质量；vp为碰撞速度。

由式（8）可知，碰撞产生的能量与碰撞速度成正比。硝铵炸药爆轰压力公式：

式中：p 为爆轰压力p0——炸药密度；D——炸药爆速；γ——炸药多方指数，常数。

平行法爆炸焊接过程中，炸药爆轰压力传递给复板，复板受到爆轰压力作用，与基板发生碰撞。由式（9）可知，p0、γ 为常数，爆轰压力与爆速平方成正比，所以爆速与单位面积装药量也是成正比[16]，碰撞压力与炸药厚度成正比。由图4（b）所示，模拟结果与理论分析符合。

上述表5 数据分析可知，3 组模拟速度与Deribas 公式计算结果均较为吻合，证明数值模拟的合理可靠性，表明Deribas 公式对镁/铝合金爆炸焊接具有较好的指导意义。

4 焊接波形分析

为观察界面波形，用上述材料炸药参数，建立二维爆炸焊接模型。将基复板粒子化，模拟结果观察到波形如图5 所示，左边为实验金相观察所得[13]，右边为SPH 二维模拟所得。实验与模拟波形基本一致，证明二维SPH 法模拟波形的可靠性。

图5 波形对比

第2 组的金相实验显示，界面波形较大，且存在融化块，焊接质量较差；王耀华[18]认为微波界面的焊接强度大于小波形界面焊接强度大于大波状界面焊接强度。故认为第3 组的焊接质量较好，第2 组金相显示，波形比第1 组略小，文献[19]认为炸药厚度的减少，炸药与复板的质量比减小，铝/镁合金碰撞角减小，结合区波形较小，与模拟结果一致。张越举等[20]认为波形的参数与碰撞速度也有关系，碰撞速度越大，越容易产生射流，易形成波形界面，与模拟结果较为一致。铝/镁合金在碰撞速度为434 m/s 时是微波结合，焊接质量较好。

为分析界面波形参数与碰撞速度与碰撞角度的关系，由模拟结果可知，第1 组在复板发生碰撞时，碰撞速度523 m/s，碰撞角14.0°，第2 组为485 m/s，碰撞角12.5°，第3 组碰撞速度434 m/s，碰撞角11.1°。如图5，第1 组振幅和波长为0.27 mm 和0.923 mm，第2 组振幅和波长0.19 mm 和0.78 mm。第三组波长0.65，波幅0.08 mm。在爆炸焊接过程中，复板对基板的碰撞速度vp可分解为x、y 轴方向，将上面三组带入计算可得：vpx1=63.74 m/s、vpy1=519.10 m/s；vpx2=52.80 m/s，vpy2=482.12 m/s；vpx3=41.97 m/s，vpy3=431.97 m/s。

该结果证明，波长与碰撞速度x 方向的速度分量有关；波幅与碰撞速度在y 方向的速度分量有关。经分析，波长和振幅随着碰撞速率的减小而减小。

5 结论

（1）采用SPH-FEM 耦合算法，建立5052/AZ31B 合金爆炸焊接的三维数值模型，并计算出铝/镁合金爆炸焊接窗口。设计的3 组实验，均在爆炸焊接窗口内部，表明复合质量较好。

（2）分析质量比对碰撞速度、碰撞压力的影响；将模拟速度与Deribas 公式计算的复板速度进行对比，模拟与理论计算较为吻合，表明Deribas公式与SPH 算法对铝/镁合金爆炸焊接的有效性。

（3）SPH 法建立二维模型，观测界面波形，与实验对比，表明SPH 法研究界面波形的可靠性；通过理论计算分析碰撞速度、碰撞角对界面波形影响，碰撞速度水平方向分量与界面波形波长成正比，竖直方向速度与波幅成正比。