蹦极加速度计算方法研究与评价分析

赵九峰

（河南省特种设备检验技术研究院，郑州 450000）

蹦极是一项广受大众喜爱的无动力游乐设施，弹跳者从高处平台跳下，依靠系在身上的弹性绳来确保安全。当弹跳者向下坠落时，展开双臂，向下俯冲，仿若雄鹰展翅，气概非凡，让弹跳者紧张刺激后体验重生的欣喜。

弹跳者从蹦极平台下落过程中瞬间加速度较大，就会产生较大惯性力[1]。弹跳者本身质量产生的惯性力会直接作用在弹跳者身上，加速度越大，惯性力越大。当加速度超过一定限度时，就会对弹跳者身体造成伤害[2]。轻则会引起弹跳者头晕目眩、呕吐等不适的生理现象，重则会危及弹跳者的生命安全。近年来，部分学者对蹦极的运行特性进行了研究，文献[3]采用ADAMS 动力学仿真与能量守恒理论计算，对绑腿式蹦极进行加速度分析；文献[4] 使用Matlab 软件对蹦极过程进行建模和仿真。以上蹦极加速度的计算过程过于繁琐，不利于实际的工程应用。

蹦极设计的一个关键是确定合理的加速度，以保障弹跳者的身体健康和生命安全[3]。而现行的标准规范并未给出蹦极加速度的计算方法，样机测试成本高，不利于实际的工程应用。基于此，本研究在蹦极运行特性分析的基础上，详细推导了蹦极的加速度方程；以国内某蹦极为例，利用瞬态动力学仿真分析技术，构建质量—弹簧系统仿真模型，获取弹性绳的变形曲线和弹跳者加速度时间历程曲线，并对其进行分析评价，以期为蹦极加速度的设计计算和校核评价提供指导。

1 蹦极加速度评价方法

游乐设施标准中规定的“加速度”与动力学中“加速度”的概念不同。为了真实反映弹跳者承受的载荷大小，游乐设施规定的加速度为惯性加速度，其大小包含重力加速度[5]。游乐设施采用G 加速度作为加速度的评价指标，G 加速度为弹跳者承受的惯性加速度与重力加速度g 的比值[6]。G 加速度是乘客承受载荷的直接反映，方向与惯性力的方向一致。

对蹦极加速度进行分析，不能直接提取运行加速度作为参数指标，需根据弹跳者承受弹性绳的拉力载荷进行换算。

由牛顿第二定律，惯性加速度a（单位为m/s2）的大小[7]：

式中：F 为惯性力，即弹跳者下落过程中弹性绳的拉力，单位为N；m 为弹跳者的质量，即体重，单位为kg。

蹦极按照束缚方式的不同分为3 种形式：绑腰式蹦极、绑胸式蹦极和绑腿式蹦极[3]。GB/T 31257-2014《蹦极通用技术条件》4.1.5 规定，绑腰式蹦极和绑胸式蹦极的加速度不应超过4.5 g，绑腿式蹦极的加速度不应超过3.5 g[8]。

2 理论分析

2.1 下落阶段分析

蹦极主要由塔架、平台和弹性绳组成，蹦极示意简图如图1 所示。

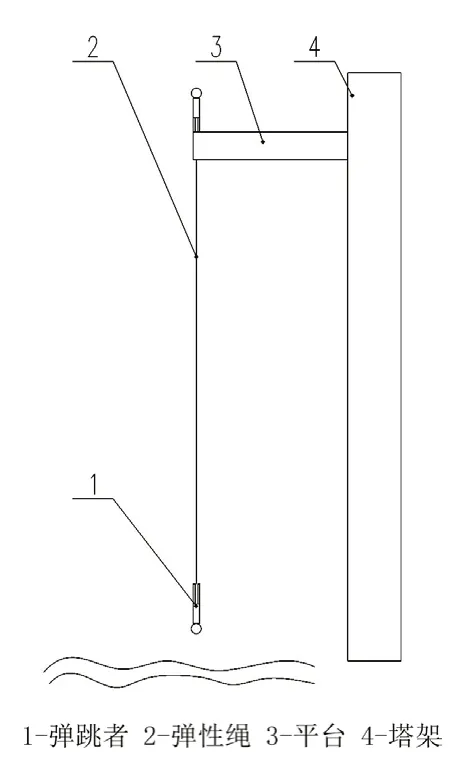
图1 蹦极示意简图

蹦极下落过程可分为4 个阶段：自由落体阶段、加速下落阶段、减速下落阶段和反复震荡阶段。

（1）自由落体阶段：弹跳者从蹦极站台跳下，开始阶段由于弹性绳未伸展开，弹跳者处于自由落体状态。

（2）加速下落阶段：当弹跳者下落一定距离，弹性绳被拉开，当拉力小于人体的重力时，弹跳者加速下落。

（3）减速下落阶段：弹性绳继续被拉长，当拉力大于人体的重力时，弹跳者减速下落。

（4）反复震荡阶段：当到达最低点时弹性绳再次弹起，弹跳者被拉起，随后又落下，这样经过多次弹起和落下，直到弹性绳不再弹起为止[3]。

蹦极所处阶段不同，弹跳者所承受的加速度也会不一样。在减速下落阶段末尾，即准备回弹的瞬间，弹性绳被拉到最长状态，此时弹跳者承受的拉力最大，加速度最大[9]。因此，可仅对蹦极的减速下落阶段进行分析研究。

2.2 加速度方程

整个下落过程中，弹跳者唯一的装备就是一条绑缚在身上的弹性绳，弹性绳作为蹦极的生命线，承载着弹跳者的自重和冲击载荷等。如果不计任何阻力，即忽略弹性绳的自重和空气阻力的影响，弹跳者和弹性绳组成的系统机械能守恒[10]。弹跳者和弹性绳的相互作用可以简化为近似的质量—弹簧系统模型描述[10]。蹦极的质量—弹簧系统模型如图2 所示。

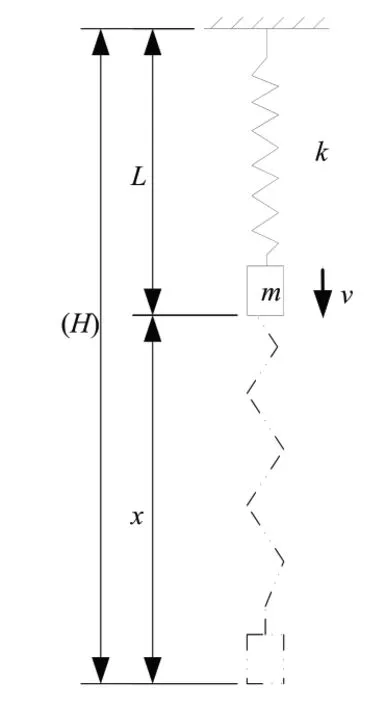
图2 质量—弹簧系统模型

初始状态，重力势能Ep（单位为J）：

式中：g 为标准重力加速度，其值为9.8 m/s2；H = L + x 为弹跳者的最大下落高度（弹性绳的最大伸长量）；L 其中为弹性绳原始长度，单位为m；x 为弹性绳最大变形量，单位为m。

第一阶段结束瞬间，仅有重力做功，机械能守恒[11]：

式中：v 为第一阶段结束时的瞬时速度，单位为m/s。

由公式（3）得第一阶段结束时的瞬时速度：

第三阶段结束，下落到最低点时，弹性绳的弹性势能Ee（单位为J）：

式中：k 为弹性绳的劲度系数，单位为N/m。

根据机械能守恒定律，下落到最低点时弹跳者的重力势能全部转化为弹性绳的弹性势能[12]，即：

由公式（2）、（5）、（6），可得弹性绳的劲度系数：

由胡克定律，可知弹跳者下落到最低位置时弹性绳的拉力[13]：

由公式（1）、（7）、（8），可得弹跳者体在蹦极下落过程中的最大加速度：

按照GB/T 31257-2014《蹦极通用技术条件》6.3.1 规定，蹦极的弹性绳在弹跳者设计载荷范围下，其最小伸长量应不小于无载长度的2.5 倍，对所有形式蹦极的弹性绳在最大动载荷下最大伸长量应不超过无载长度的4 倍[8]，即：

联立公式（9）、（10）、（11），可得蹦极的G 加速度方程：

3 实例计算

3.1 瞬态动力学模型

Workbench 是ANSYS 公司开发的协同仿真平台，提供了开放的框架结构，将产品设计所需的各种分析工具整合在一起，并且以图形化的方式管理工程分析过程，实现基于虚拟样机的线性、非线性、静力、动力等仿真模拟分析[13]。瞬态动力学分析为Workbench 集成下的一个分析模块，主要用于分析结构在任意随时间变化载荷作用下的响应[14]。以某景区一高空蹦极为计算对象，蹦极弹性绳无载荷时的原始长度L=20 m，劲度系数k=50 N/m，蹦极设计载荷，即弹跳者的体重范围为m=50~100 kg。

蹦极弹性绳由橡胶材料制成，具有密度小、弹性大的优点，20 m 弹性绳的自重约为4 kg，由于弹性绳自重较小，可忽略弹性绳的自重影响[3]。利用Workbench 的瞬态动力学分析模块，构建质量—弹簧系统模型，蹦极弹性绳用等效弹簧来代替，设置弹簧的刚度k 为50 N/m，设置弹簧的阻尼系数为0[15]。

以弹性绳伸展到原始长度时为仿真计算的初始状态，由公式（4）可得初始状态时弹跳者的瞬时速度:。

弹簧顶部施加全约束，弹跳者的初始速度设置为19.8 m/s。整体施加向下的重力加速度9.8 m/s2，蹦极动力学模型如图3 所示。

图3 蹦极动力学模型

3.2 加速度评价

定义仿真分析时间为4 s，最小时间步为0.01 s，由于弹性绳大变形为位移非线性问题，求解设置下定义大变形（Large Deflection）选项为打开状态（On），进行大变形瞬态动力学分析。弹跳者质量m=50 kg 时，蹦极仿真计算结果如图4 所示。

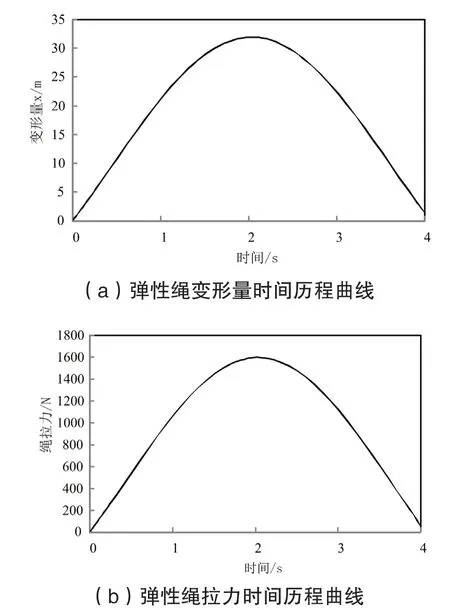
图4 蹦极仿真计算结果（m=50 kg）

由图4（a）可知弹跳者质量m=50 kg 时，弹性绳的变形量在2.0 s 达到最大值x=31.9 m，最大伸长量H=20 m+31.9 m=51.9 m，弹性绳伸长量与无载长度的倍数n=51.9/20=2.60；此时弹性绳拉力在2.0 s 达到最大值F=1590 N，由公式（1）可得加速度a=1590/50=31.8 m/s2，换算为G 加速度3.24 g。

同理，在瞬态动力学分析软件中对其他不同体重弹跳者进行仿真计算，不同体重弹跳者蹦极仿真计算结果如表1 所示。

表1 不同体重弹跳者蹦极仿真计算结果

从表1 的仿真结果可知，随着弹跳者体重的增加，蹦极加速度逐渐减小；弹跳者体重为50 kg时加速度最大，该蹦极的最大加速度为3.24 g，小于标准规范要求的3.5 g，表明该蹦极加速度满足规范要求；该蹦极弹性绳伸长倍数的范围为2.60~3.69，满足标准规范要求的2.5~4。

蹦极加速度的仿真结果和解析结果对比曲线如图5 所示，不同体重弹跳者蹦极加速度结果对比如表2 所示。

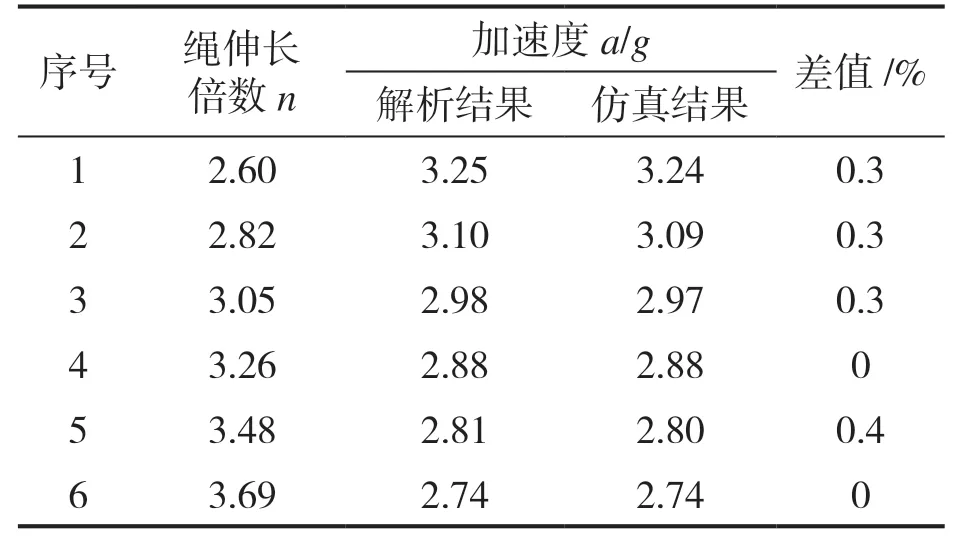
表2 不同体重弹跳者蹦极加速度结果对比

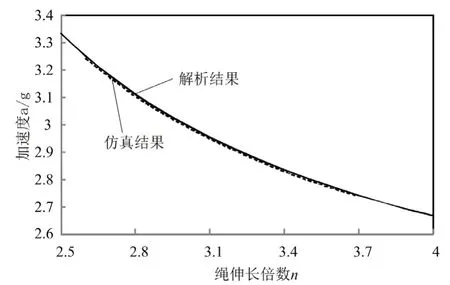
图5 蹦极加速度对比曲线

由图5 可以看出，蹦极理论计算的加速度范围为2.67 g~3.33 g；蹦极弹性绳的伸长倍数不断增大，蹦极加速度不断减小；由表2 可以看出，仿真结果和解析结果的偏差很小（不到1%），仿真结果基本与理论计算结果相符，表明了仿真结果的可靠性。

综上，蹦极理论加速度的最大值为3.33 g，小于标准规范中绑腿式蹦极加速度3.5 g，更远小于绑腰式蹦极和绑胸式蹦极加速度4.5 g 的要求。因此，GB/T 31257-2014《蹦极通用技术条件》限定弹性绳伸长倍数的前提下，无需再重新限定蹦极加速度的范围。

4 结论

加速度作为蹦极重要的设计参数，关系到乘弹跳者的生命安全。在对蹦极运行特性分析的基础上，结合实例对蹦极在不同体重下分别进行瞬态动力学仿真计算，并对其加速度仿真结果和解析结果进行对比和分析，得出以下结论：

（1）蹦极加速度只与弹性绳伸长倍数有关，随着伸长倍数的增加，加速度逐渐减小。

（2） 蹦极理论加速度的范围为2.67 g~3.33 g，小于规范要求的加速度值，规定蹦极弹性绳伸长倍数，就等同于规定蹦极的加速度，规范中无需再规定蹦极的加速度。

（3）对某蹦极进行仿真计算，弹性绳的伸长倍数和蹦极加速度均满足规范要求，仿真结果与解析结果的最大误差小于1%，表明仿真计算结果可靠。

（4）对于某一确定的蹦极设备，弹跳者体重不同，蹦极的加速度也不同，在实际运行过程需精确计算并严格限定弹跳者的体重范围，以保障弹跳者的生命安全。