运动能力标准化评价的研究——基于NBA选秀测试成绩标准分数及TSA的分析

赵祎凡，赵可伟

测试是评价运动能力、评估训练效果及获取训练反馈的重要手段（Haff et al.，2021）。对运动员进行阶段性测试，并对数据进行长期跟踪分析，有助于为训练过程建立导向，提高训练效率；科学的测试同样是竞技运动后备人才选拔和培养的重要抓手（杨建军 等，2017），是推动不同年龄运动员选材体系构建的有效工具（黄玺章 等，2021）。运动员选材作为全球竞技体育“军备竞赛”的九大支柱之一（De Bosscher et al.，2008），对测试数据进行纵向、横向比较有助于甄别精英运动员竞技能力的关键指标，推动冠军模型的建立（庄薇等，2018）、跨界跨项选材路径的实施（黎涌明 等，2018；田麦久 等，2018）。充分发挥测试的价值，不仅需要对测试内容的有效性和科学性进行探究，更需要对测试内容的评定标准进行科学探索，对测试数据进行可靠的解释（Drinkwater et al.，2008）。但目前我国各级各类运动能力测试的评价标准尚待完善（沈巧儿 等，2001）。因此，基于运动能力测试与评估的现实诉求，以及运动员选材、选拔科学化发展的长远考虑，有必要对运动能力标准化评价的可行性路径进行深入研究。

由于各种运动能力测试的原始成绩通常只能用于评估一种或部分运动能力的表现水平（Glassbrook et al.，2022），例如纵跳、冲刺跑等测试只能反应运动员的跳跃、速度能力，单个测试直接测量的原始成绩（分数）无法反馈与评估运动员在所有测试中的综合能力与整体水平，因此，选材、选拔测试及体能测试都需要设置多种不同测试类型，以全面评估运动员的运动能力（Burr et al.，2008；Drinkwater et al.，2008），各类测试还需要针对不同项目的竞技特征制定不同的评价标准。此外，由于不同测试成绩之间单位不同，导致成绩无法通过直接相加来对总体运动能力进行评估和解读。

基于标准化评价及全面评价的思考，有学者提出运动能力总分（total score of athleticism，TSA）的数学评价模型（Turner，2014；Turner et al.，2019）。该方法通过标准分数将原始成绩转化为统一标准的“位置分数”，弥补原始分数无法相加及加权比较的不足，经过转化后的分数并未改变原始数据的分布形态。TSA通过将所有测试的标准分数汇总（均值或相加），直接对运动员在所有测试中表现出的运动能力水平进行整体评价。其主要计算方法为Z分数和T分数（表1）：Z分数主要利用标准差，在原始分的基础上得出结果；T分数（TSA-Ta）则是对Z分数进行线性转换，更符合百分位记数的实践应用场景。已有相关研究将Z分数应用于儿童少年健康水平的评估中（Eisenmann et al.，2011）；也有研究应用TSA评估橄榄球不同位置球员运动能力差异对场上表现的影响（Philipp et al.，2022），并建立不同位置球员的运动能力特征模型。但TSA在实践应用中的有效性尚待检验。基于此，本研究旨在检验体能测试成绩标准化得分及TSA在实践应用中的有效性。

表1 TSA计算方法Table 1 Calculation Methods of TSA

1 研究对象与方法

1.1 数据来源

数据来源于NBA选秀开放数据库（http：//stats.nba.com/draft/combine）中的体能测试。美国职业篮球联赛选秀综合测试（National Basketbal Association Draft Combine，NBA DC）是评估NBA选秀球员的一项综合测试，包括人体形态测量（anthropometric measurements）、体能测试（strength and agility test）和技术测试（spot-up shooting）等，已被证明能有效预测运动员的运动表现（Teramoto et al.，2018）。本研究选取2000—2022年NBA DC中运动员各项测试的标准分数及TSA作为研究对象。按照TSA规定的计算方法，对NBA DC中的体能测试数据进行Z分数标准化处理，随后按照选秀年份分别计算相应的TSA分数（平均值算法）并进行排名。依据NBA选秀测试的要求，所有受试者都年满19岁，依据选秀时登记的第一位置对场上位置进行记录。剔除测试数据不全的样本，结果共有1 552个样本纳入分析。

1.2 研究方法

1.2.1 文献资料调研

相关文献资料显示，目前我国不同水平运动员运动能力测试中尚无广泛应用的标准化评价方法，TSA作为衡量运动员整体运动能力的一种数学方法尚未得到有效检验，鲜见相关研究。鉴于此，通过梳理国内外相关研究，汇总TSA不同算法，最终确定本研究的研究方向。此外，NBA DC开放数据库中的相关体能测试数据，为本研究提供可靠的数据来源。

1.2.2 数理统计

利用IBM SPSS 25软件进行统计分析。经K-S检验后，服从正态分布的数据以平均值±标准差（M±SD）表示，偏态数据以中位数（四分位距）［M（IQR）］表示。

将参加2000—2022年NBA DC的篮球运动员分为入选组与落选组，对TSA、排名和选秀结果进行统计分析（表2）。经K-S检验，将入选组与落选组体能测试的Z分数、TSA得分及排名中符合正态分布的数据采用独立样本t检验，非正态分布数据采用曼-惠特尼U检验（Man-WhitneyUtest），比较组之间是否具有差异。采用肯德尔相关系数（Kendall tau-b correlation coefficient）对各项测试的Z分数与选秀结果、TSA得分与选秀结果、TSA排名与选秀结果之间的相关性进行检验，肯德尔相关系数（τb）为其效应量。此外，对不同位置球员的Z分数、TSA得分及排名的差异性进行统计分析。经K-S检验，各组数据部分符合正态性，故采用适用于多独立样本总体分布的非参数克鲁斯卡尔-沃利斯H检验。P＜0.05表示差异具有统计学意义。

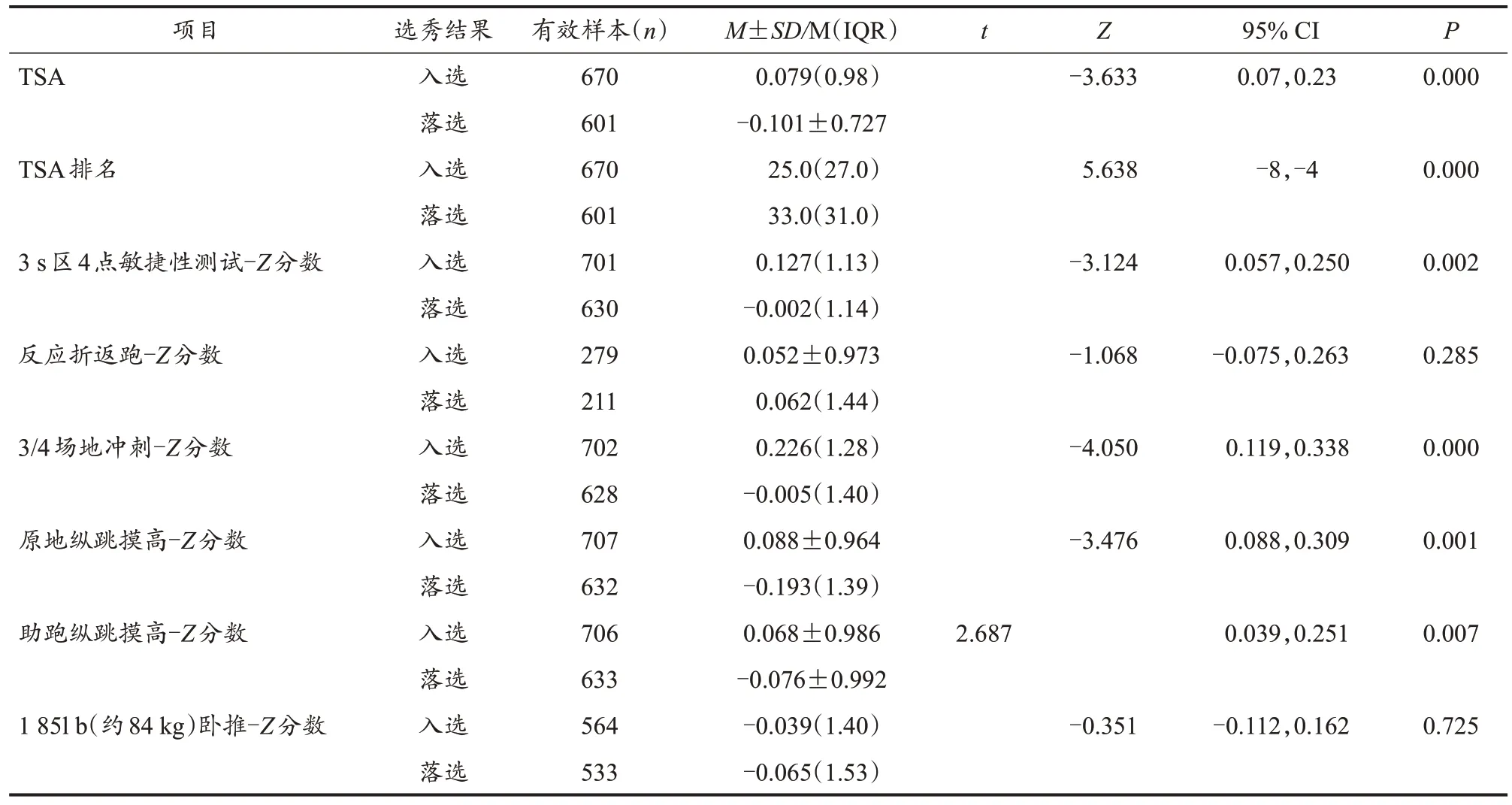
表2 NBA入选、落选球员体能测试Z分数及TSA的统计检验结果Table 2 Statistical Results of Z-score and TSA of Strength and Agility Test for Drafted and Undrafted Players from NBA DC

2 研究结果与分析

2.1 TSA、Z分数与NBA选秀结果

Z分数和TSA的统计分析显示（表2），入选组与落选组TSA得 分（Z=-3.633，P＜0.01）、排 名（Z=5.638，P＜0.01）的差异具有统计学意义，入选组的体能测试TSA得分高于落选组，TSA排名更靠前；入选组与落选组各项测试的Z分数均存在不同程度的差异。入选组与落选组在3 s区4点敏捷性测试（Z=-3.124，P=0.002）和3/4场地冲刺（Z=-4.050，P=0.000）的Z分数差异具有统计学意义。有研究发现（Cui et al.，2019），这2项测试入选球员的表现优于落选球员，表明对体能测试的成绩进行标准化处理能有效反馈运动员在测试中的相对水平。入选组的原地纵跳摸高（Z=-3.476，P=0.001）和助跑纵跳摸高（t=2.687，P=0.007）的差异也具有统计学意义，表明入选球员的纵跳能力更强。此外，对纳入的6项体能测试的Z分数、TSA得分、排名与选秀结果进行肯德尔相关系数检验发现，各变量之间的相关性存在不同程度的统计学意义（图1），TSA得分（τ=-0.083，P＜0.01）、排名（τ=0.130，P＜0.01）与选秀结果的相关性存在统计学意义。上述结果表明，TSA得分、排名可为NBA选秀提供一定参考，在保证测试内容有效的前提下，Z分数和TSA可在选拔相关测试中充分发挥甄别优秀运动员的作用。

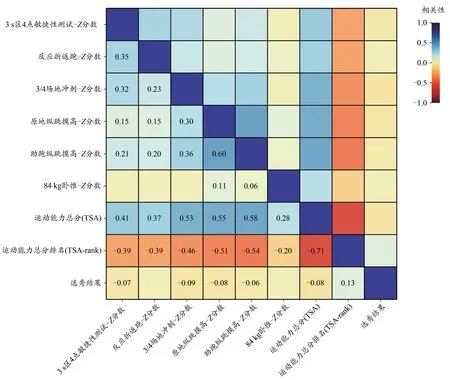
图1 肯德尔相关性系数热力图Figure 1. Kendall Tau-b Correlation Coefficient Heat-Map

2.2 不同位置选秀球员的Z分数与TSA差异分析

克鲁斯卡尔-沃利斯H检验发现，5个不同位置球员的TSA得分（H=153.11，P=0.000）及排名（H=162.26，P=0.000）存在不同程度的差异，控球后卫和中锋的TSA得分（P=0.000）、排名（P=0.000）差异较为显著，后卫TSA得分（P=0.956）、排名（P=0.973）之间的差异不存在统计学意义（表3）。比较“3 s区4点敏捷性”测试的Z分数发现，控球后卫与得分后卫之间的差异不存在统计学意义（P=0.179），而其他各位置的差异均存在统计学意义；反应折返跑方面，控球后卫与得分后卫（P=0.093）、大前锋与中锋（P=0.066）之间的差异不具有统计学意义，其他位置则存在一定差异，这可能是由于外线球员的变向能力（Stojanović et al.，2019）优于内线球员所致。“3/4场地冲刺”的Z分数同样呈现后卫之间的差异不存在统计学意义（P=0.068），其他各位置的比较均存在一定差异，可能是由于外线球员的直线加速能力（Scanlan et al.，2014）更强。“原地纵跳摸高”的Z分数比较发现，控球后卫与得分后卫（P=0.300）、控球后卫与小前锋（P=0.984）、得分后卫与小前锋（P=0.321）之间的差异不存在统计学意义，其他位置的比较存在一定差异。“助跑纵跳摸高”的Z分数同样发现后卫（P=0.494）、控球后卫与小前锋（P=0.485）、得分后卫与小前锋（P=0.165）之间的差异不存在统计学意义，其他位置之间存在差异，尤其是后场球员显著优于前场球员，可能是由于中锋球员的跳跃能力明显弱于其他位置球员（Boone et al.，2013），而腿部力量是后卫球员入选的关键指标（Cui et al.，2019）。卧推方面，控球后卫与得分后卫不存在差异（P=0.701），小前锋、大前锋以及中锋之间不存在差异，但后卫和其他位置球员均存在差异。TSA得分及排名在内外线球员之间同样表现出一定差异。上述结果表明，内线、外线球员之间的体能测试Z分数、TSA得分及排名具有一定差异；后卫之间、锋线之间的差异较小，后卫与小前锋在大部分测试中差异也较小，但后卫与中锋、大前锋之间有较大差异，后场球员在大部分测试中的Z分数及TSA均优于前场球员。

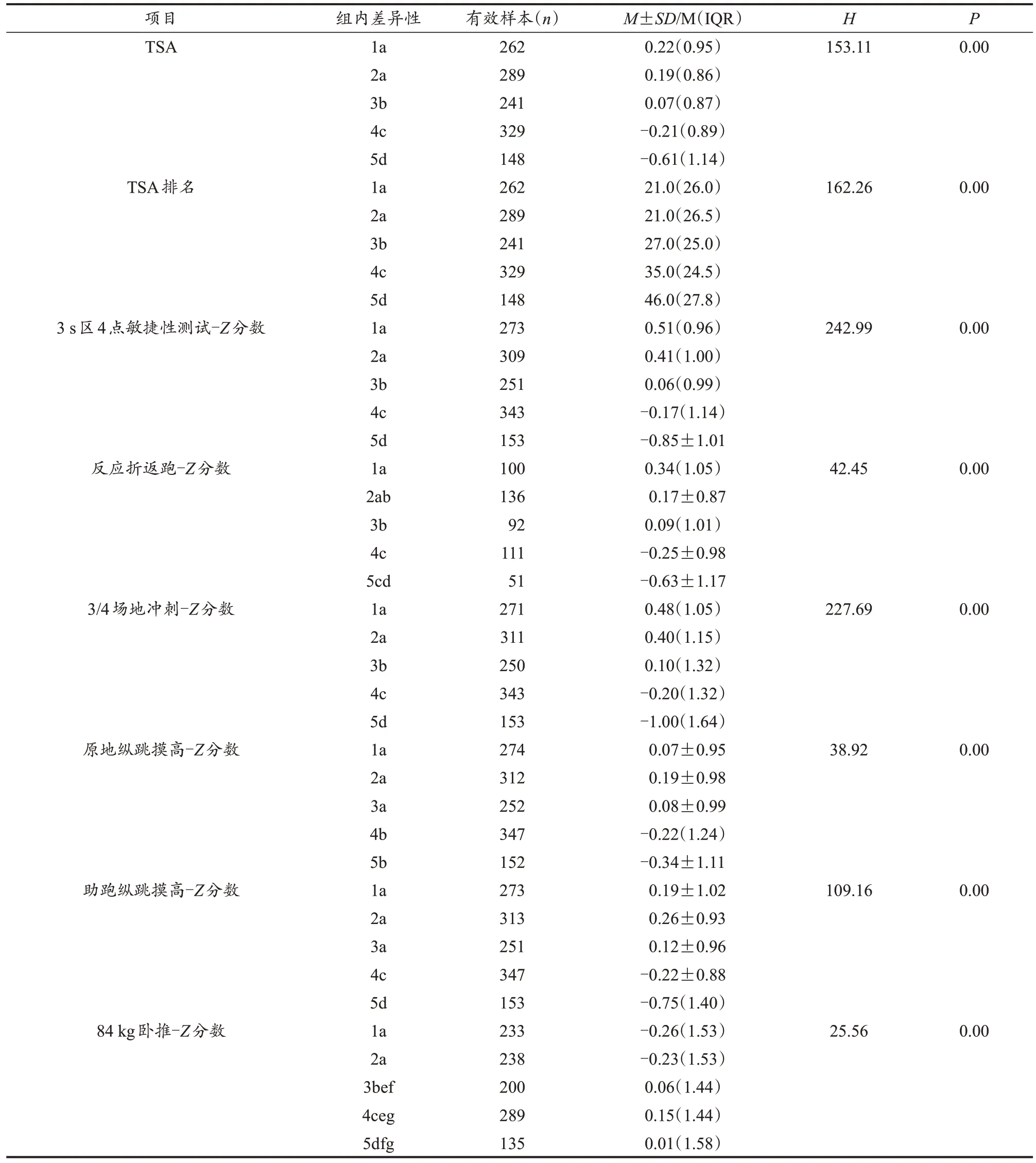
表3 不同位置球员TSA及Z分数的非参数检验结果Table 3 Non-parametric Test Results of Z-score and TSA of Players in Different Positions

不同位置的篮球运动员体能特征显著不同（Ben Abdelkrim et al.，2010）。Stojanović等（2018）发现，后卫在比赛中的冲刺跑及高强度折返跑比前锋和中锋更多，站立和行走更少，血乳酸浓度和心率更高。基于19岁精英球员的时间-运动分析同样发现，在篮球比赛中后卫的体能需求水平更高（Ben Abdelkrim et al.，2007）。Z分数及TSA分析的结果与篮球运动的专项表现特征（Morrison et al.，2022）相吻合，可以在NBA DC中有效区分不同位置球员的运动表现特征。

3 实践应用及局限性

3.1 标准分数及TSA的应用目的与意义

数字化带动训练科学化是现代高水平竞技运动取得突破的关键（彭国强 等，2020）。竞技运动领域内的运动能力测试主要用于选拔优秀运动员或对竞技能力、运动表现水平进行诊断（Bangsbo et al.，2006），最终都要对测试结果进行评价性决策。本研究对NBA DC数据的统计结果已经证实，TSA可直接筛选出水平较高的运动员，可有效应用于运动选材。此外，对NBA DC中不同位置球员测试成绩的标准分数及TSA的比较，能有效识别其体能特征，可据此提高未来训练的针对性和指向性。借助标准分数及TSA对不同项目的测试成绩进行研究，有助于对各项目的体能特征进行甄别（Ziv et al.，2009）、解决测试与评价中的难点，并发挥测试的导向作用（Fernandez-Fernandez et al.，2014）。值得注意的是，科学的评价需要建立在可靠、有效测试的基础上（Mayorga-Vega et al.，2016）。

3.2 标准分数及TSA的局限性

标准分数及TSA可有效划分运动员的相对水平，为评价和选拔优秀运动员提供借鉴与参考。但二者在实践应用中也存在一定局限性：1）个体的标准分数呈现的是位置分数，只能进行评估对象之间的横向比较，若要建立可靠的参考值范围则需要在大样本的基础上做进一步统计分析，建立对应人群的常模参考分数体系；2）TSA对标准分数直接平均或相加的算法没有区分不同运动能力的权重因子。有研究建议对Z分数进行加权计算（Jones et al.，2017），以此突出运动员竞技能力结构的差异性，未来还需针对加权因子展开相关研究。

目前，基于正态分布的离差法（陈佩杰 等，2013）已经广泛应用于体质健康评价标准中（李岩松 等，2019），基于成绩分布的TSA方法在运动能力测评中还未广泛应用，相关研究亟需推进。此外，实践应用中的选材、测试与评估面对的人数通常较少，Z分数并不能很好地解释均值的差异幅度。小样本计算方法（TSA-Tb）（Field，2013）的有效性和可靠性尚未得到检验，在选材、测试与评价方面的研究有待进一步推进。

4 研究结论与建议

依据现有文献及数理统计结果，本研究认为，标准分数及TSA是进行运动能力横向比较的有效工具，两者可直接用于竞技运动测试的评价，以提高选材效率；也可利用其识别运动员测试成绩的表现特征了解特定人群的常模参数，推动运动员选材体系及运动能力测试标准等研究的开展。

由于标准分数及TSA的应用处于起步阶段，在实践中还需更多研究进行丰富完善，建议未来的研究可着眼于：1）利用标准分数及TSA展开选材相关研究，深入探究不同项目、不同年龄运动员运动能力的表现特征，形成可靠的评价体系；2）利用标准分数及TSA对不同项目运动员体能测试数据进行分析，研制各项目的体能数据模型，科学制定不同项目体能测试评价标准；3）对小样本算法下TSA应用的有效性展开相关研究，为其实践应用提供理论依据。