钝体表面附着物对低速水流压电俘能器性能影响研究1)

孙维鹏 刘宸涵 郁小彬 胡 珅 钟可欣 赵道利,2)

* (西安理工大学省部共建西北旱区生态水利国家重点实验室,西安 710048)

† (华东天荒坪抽水蓄能有限责任公司,杭州 310012)

引言

近年来,能源危机愈演愈烈[1],为了应对新环境下全球能源格局发生的深刻调整[2],高效开发利用可再生能源迫在眉睫[3-6].水能作为占比最高的可再生能源,如何高效利用一直备受关注.天然河道中的高速水流能可通过水轮发电机组加以利用[7-8],这一技术目前已相对成熟;而湖泊与小型河流中的低速水流能虽可作为新能源的重要补充,但因其分布广、能量低而存在利用困难的问题.驰振[9]作为一种能够发生在低速水流中的现象,有流速响应范围宽和无锁定限制的特点.因此基于驰振设计且已在流场中展现出游优异性能的驰振式压电俘能器为低速水流能的利用提供了解决方案[10].利用驰振式压电俘能器将低速水流能量转化为电能,可以为微机电系统[11-12]和无线传感器[13-14]供电.

目前已经存在一些关于利用低速水流能的压电俘能器研究.曹东兴等[15]设计一种利用永磁铁增强流致振动的压电俘能器.实验结果表明: 水流速度为0.5 m/s 时,输出功率的均方根值为120 μW,与无附加磁体的压电俘能器相比提高了57.8%.单小彪等[16]提出一种在水中完全淹没的尾流激振式压电俘能器.结果表明,当钝体的直径为15 mm 时,在上游距其中心20 mm 处放置直径5 mm 扰流柱能够使压电俘能器输出23.35 V 的电压,与没有扰流柱相比输出电压提升了51%.Liu 等[17]基于驰振的触发方式,提出一种新的时间变流型方法.该方法解释了传统的时间平均流型方法难以解释的横向驰振机制.Lian 等[18]研究钝体截面为正方形、三角形和圆形的压电俘能器在水中的性能.实验表明: 截面为三角形的钝体,其振幅比大于1.8;圆柱型钝体的能量转化率最高为80%.燕翔等[19]实验研究T 型截面钝体的驰振特性,并进一步探究其在不同外力条件及不同截面宽高比和阻尼比条件下的振动响应差异.He 等[20]通过研究证实改变钝体的几何形状,可以实现耦合或独立的驰振和涡激振动.Zhao等[21]采用圆柱形扰流柱,对钝体截面形状为圆形、D 形和倒D 形的压电俘能器进行水槽实验测试.结果表明,3 种压电俘能器的采集功率分别达到570.3,596.4和1074 W/m3,是无尾流激励情况的43.2,25.3 和31 倍.张军等[22]对三棱柱的流致振动进行了实验研究,并评估其能量转化效率.Song 等[23]研究圆柱型钝体压电俘能器在不同直径、质量和阻尼比条件下的输出性能.研究证实在一定范围内,降低质量和增加钝体直径都可以提高压电俘能器的输出.以上研究主要通过改变钝体的形状来优化压电俘能器,而在钝体表面添加小型附着物的研究还很少.

存在于钝体表面的附着物能够影响压电俘能器系统的振动与输出[24-25],目前已存在一些将附着物与压电俘能器相结合的应用: Zhu 等[26]提出一种由圆柱体和五角星组成的新型压电俘能器,双向流固耦合仿真的结果表明其功率密度可达到885 W/m3.Hu 等[27]通过调整圆形、三角形和矩形杆件在圆柱形钝体上的位置来提升设备的风能量采集效率.实验证实当安装的三棱柱夹角为60°时,能量采集器的性能最佳.Zhu 等[28]设计了在圆柱体表面安装对称鳍状条带的新钝体,数值模拟的结果表明收集到的最大功率超过60 W/m.目前关于附着物在压电俘能器上的研究都只局限于其形状及安装形式,缺少在钝体上进行切除特定形状的尝试.附着物的凸起高度和凹陷深度值对压电俘能器性能的影响有待研究.

综上所述,本文主要研究不同凸起高度/凹陷深度和形状的附着物对驰振式压电俘能器输出特性的影响.引入水的附加质量力改进现有的分段参数模型.基于准稳态假设,建立驰振的水动力模型并计算出驰振力.水槽实验验证了数学模型的准确性,进一步通过模型分析压电俘能器的输出功率和悬臂梁振幅与凸起高度/凹陷深度之间的关系.最后基于数值模拟从流体动力学的角度阐述超表面对系统影响的根本原因.

1 数学模型

本节利用拓展的哈密顿原理推导出压电俘能器的机械控制方程,引入高斯定理建立电场-位移控制方程,并基于准稳态假设计算驰振的水动力及力矩,利用伽辽金法离散悬臂梁的位移,并在此基础上解耦控制方程,得出输出功率和悬臂梁位移的近似解.

1.1 俘能器机械控制方程

本文研究的压电俘能器由钝体、悬臂梁和MFC压电片组成,如图1 所示.悬臂梁的上端固定,中部黏贴有压电片,下端与钝体连接.x轴为悬臂梁的长度方向,y轴为水流方向,受到水流冲击的钝体在z方向上发生振动,考虑到振幅较大,选择脆性低、韧性高的宏观纤维复合材料(macro fiber composites,MFC)作为压电材料.

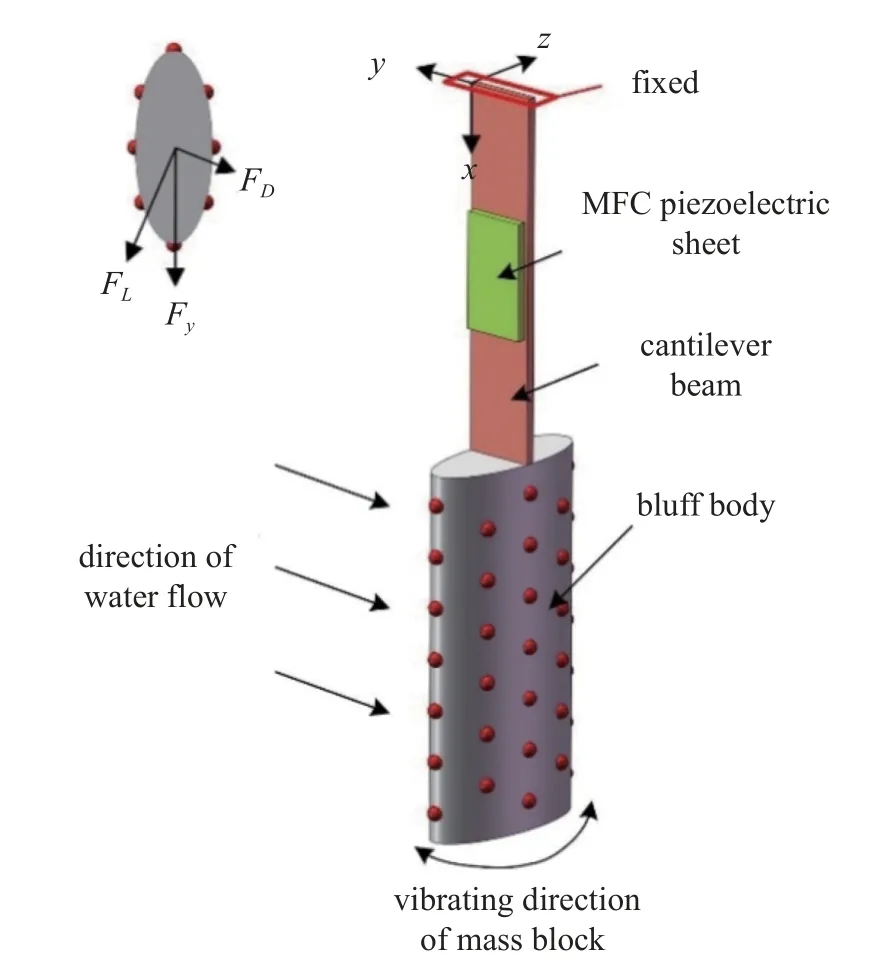
图1 压电俘能器Fig.1 Piezoelectric energy harvester

椭圆柱钝体的表面装配了人工设计的附着物,其形状采用椭球型和圆柱型两种,各自的最大高度被定义为特征值,分别为Eell和Ecy,如图2 所示.椭球型和圆柱型附着物的特征值均设置为6,4,2,-1 和-2 mm,其中正值为凸起,负值为凹陷.

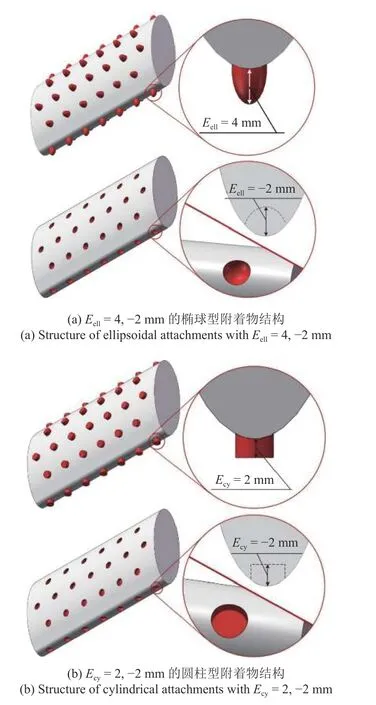
图2 附着物的结构图Fig.2 Structural diagram of the attachments

基于拓展的哈密顿原理[29-30],压电俘能器的控制方程可表示为

式中,ν(x,t) 表示t时刻悬臂梁x处的位置在z方向上的位移;ca和cs分别表示悬臂梁的气动阻尼系数和黏性应变系数;δ表示克罗内克符号,其值在x=l时取1,反之取0;ϑP为压电耦合系数,ϑP=-e31bp·(z1+z2)/2,e31为压电应力系数,e31=Epd31,d31为压电层的应变系数;V(t)压电材料的电压;Ftip和Mtip分别表示悬臂梁的驰振力和力矩.

1.2 电场-位移控制方程

引入高斯定理[31]

系统电场-位移控制方程可表示为

式中Cp是压电俘能器的电容,表示为

1.3 驰振的水动力计算

为了建立驰振的水动力模型,引入准稳态假设.而假设中的驰振力会受到攻角α的影响.攻角可表示为

而攻角与驰振系数Cy存在如下关系

式中a1和a3可通过实验获得.

考虑到附加质量力对驰振力的影响,钝体单位长度的驰振力可表示为[32]

式中CM表示附加质量系数.

悬臂梁所受到的驰振水动力和力矩可由下式计算

1.4 驰振模型的机电解耦

应用伽辽金法[33-34]离散悬臂梁的位移ν(x,t),将其划分为空间变量和时间变量

式中,Qi(t)和φi(t)分别为悬臂梁的第i阶模态坐标和模态.

驰振一阶模态的水动力可以根据f(t)=φ(l)Ftip+φ′(l)Mtip来计算.依据式 (7),得出一阶模态的水动力

式中,k1,k2和k3分别为

Abdelkefi 等[35]的研究证实,悬臂梁的振动主要受一阶模态支配,Bibo 等[36]也发现一阶模态满足被捕获的条件.因此本文采用一阶模态来简化悬臂梁的机电耦合模型

式中,ζ表示阻尼系数;ω表示压电俘能器的一阶固有频率;θp是压电耦合项,表示为 θP=ϑP[φ′(l2)-φ′(l1)];f(t)表示一阶振型的水动力.解耦的控制方程[37]由式 (9) 和式 (10) 得

式中,ϖ和Ce分别为压电俘能器的修正频率和阻尼,表示为

进一步可得位移模态坐标与电压之间的关系

模态坐标的振幅为

由式 (14) 确定模态振幅Q0后,压电俘能器的采集功率可表示为

2 实验设置

本研究的实验部分在图3 所示的U 型水槽中进行.水从地下水库通过泵与进水管被引入矩形薄壁堰中,薄壁堰上游的蜂窝网可以降低水的湍流,从而减少水流不稳定对上游水位探针读数的影响;水流离开水堰流经第一段长直段,在这里被充分稳定以满足实验段对稳定水流的需求;随后水流流入实验段,实验段的中部安装了压电俘能器;最后水流由尾水口流回地下水库.实验段的长度为6.2 m,其断面宽度为0.4 m.实验中的流速是通过泵阀门及尾水口上方的电动阀门控制的,转动泵阀门能够调节进入水槽内的流量;调整电动阀门的高度可控制水槽内的水位,然后利用流量计算公式得出流速.

图3 U 型水槽Fig.3 U-shape water channel

压电俘能器的钝体、悬臂梁及MFC 压电片的参数如表1 所示.本实验的流速范围为0.26～0.51 m/s,取0.05 m/s 为一流速步长.实验中利用示波器测试出与压电片串联的负载电阻的电压并将数据储存在计算机,然后计算出电压的均方根值(RMS voltage).实验的负载电阻值为3.5×105Ω.

表1 钝体、悬臂梁和压电片的物理参数Table 1 Physical parameters of bluff body,cantilever beam and piezoelectric sheet

3 模型验证

为了验证所建立数学模型的准确性,分别绘制0.41,0.46 和0.51 m/s 流速下椭球型和圆柱型附着物在2 mm 凹陷条件下电压与预测值的对照,如图4所示.图中的实线为实验测得的电压曲线,是从单次140 s 的实验电压中选取相对稳定的4 s 绘制的;虚线为电压的数学模型计算值.图中实线和虚线基本重合,二者之间的微小差异是由水流的轻微波动引起的.所建立数学模型的计算结果与实验结果十分吻合,由此验证了数学模型的准确性.

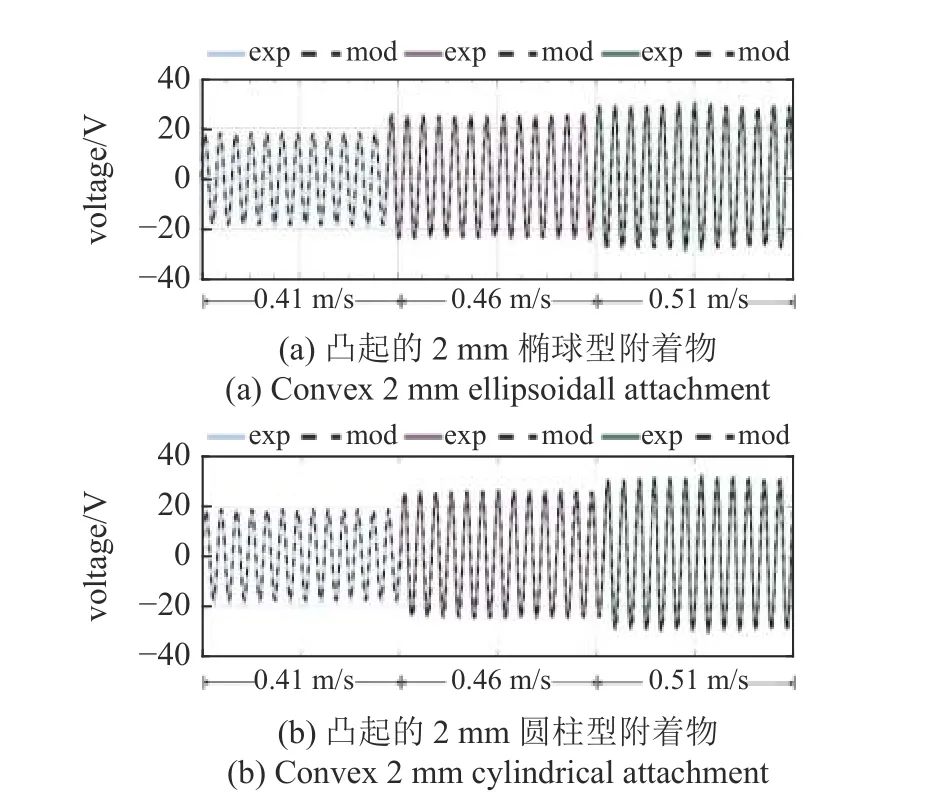
图4 模型计算和实验结果的时域曲线对比Fig.4 Comparison of time histories of the model calculations and experimental results

4 压电俘能器输出特性和悬臂梁振幅的分析

结合实验值和数学模型的近似解,分析椭球型和圆柱型附着物在不同的特征值和流速条件下对驰振式压电俘能器RMS 输出功率和钝体振幅的影响.

4.1 流速对压电俘能器输出特性影响的分析

椭球型附着物的压电俘能器RMS 输出功率随流速的变化如图5(a) 所示,可以看出在所有特征值下,压电俘能器的输出均随着流速的增加而增加.这是由于钝体的振幅随流速而增大,从而带动压电片发生更大程度的形变进而产生更高的电压,符合驰振的特性.此外附着物的特征值对压电俘能器输出功率的影响也不同.在U=0.51 m/s 的流速下,Eell=-2 mm 的压电俘能器RMS 输出功率为1.411 mW,相比于椭圆柱增幅为69.88%;而部分特征值的附着物则抑制压电俘能器的输出: 当Eell=6,4 mm 时,压电俘能器的RMS 输出功率在各个流速下始终低于未包裹附着物的椭圆柱,其中U=0.51 m/s 时,6 mm 特征值的椭球型附着物使输出功率降低了80.02%.

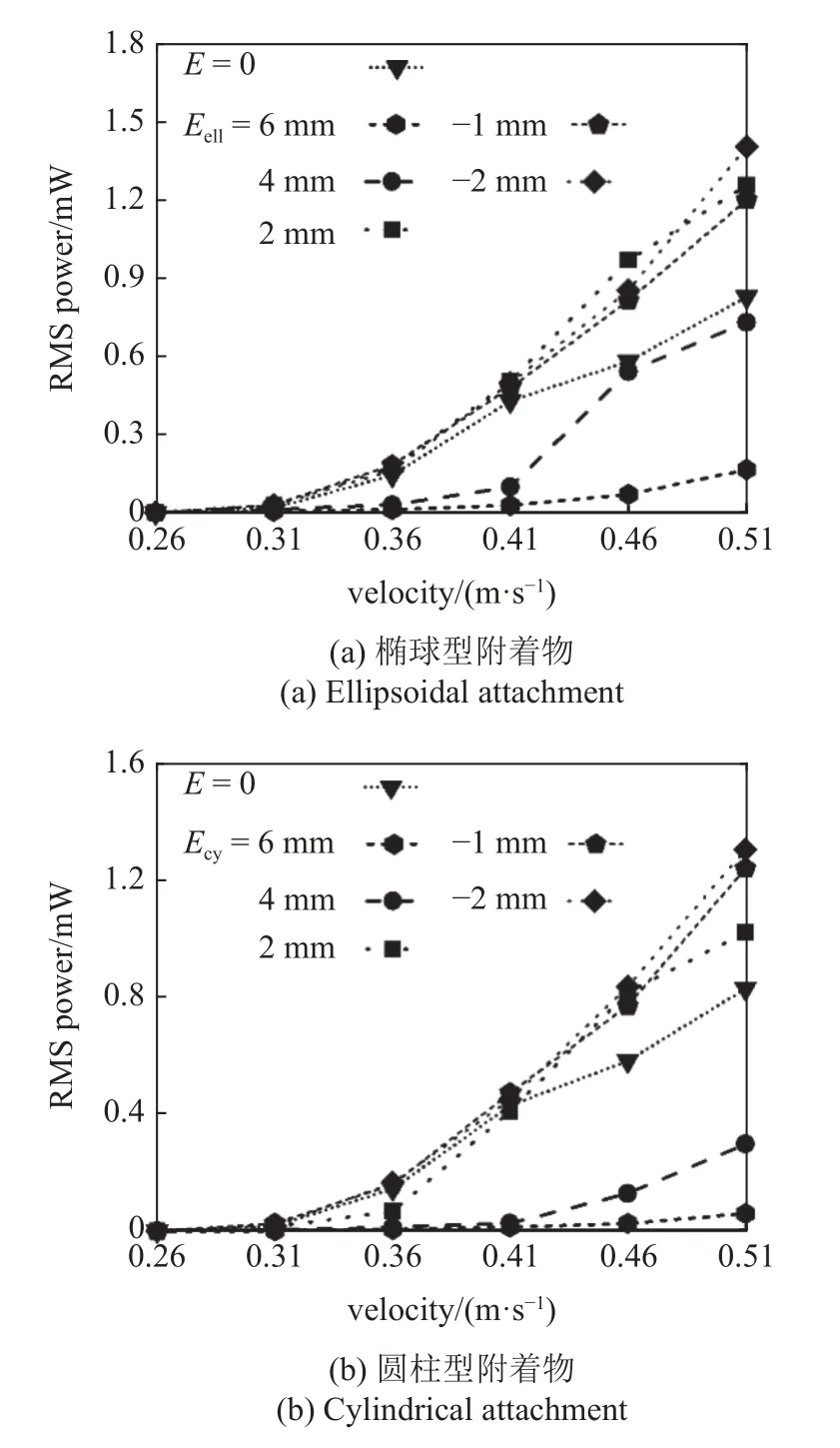
图5 流速对压电俘能器RMS 输出功率的影响Fig.5 Effect of flow velocity on the RMS output power of the piezoelectric energy harvester

图5(b) 展示了包裹圆柱型附着物对压电俘能器性能的影响.与椭球型附着物相比,圆柱型附着物的施加使得压电俘能器的出输出整体偏低.当Ecy=4,6 mm 时,压电俘能器在所有流速下的输出均被大幅度抑制,其中Ecy=6 mm 的压电俘能器在U=0.51 m/s 的输出为0.059 mW,降低了92.9%.此外随着流速的不断增加,Ecy=-1,-2 mm 在流速超过0.41 m/s 后能够提高输出功率,其中Ecy=-2 mm 在0.51 m/s 的流速下能够产生1.308 mW 的RMS 功率.

4.2 特征值对压电俘能器输出特性的影响

4.1 中比较了不同特征值下流速对于压电俘能器RMS 输出功率的影响,接下来结合数学模型的计算结果,进一步分析特征值的变化对于压电俘能器性能的影响.图6(a) 表明随着特征值从-2 mm 逐渐增大到6 mm,椭球型附着物压电俘能器的输出先减小再增大后减小的趋势,最大值分别在Eell=-2,2 mm 处.这说明当特征值绝对值在0 附近,即凸起或凹陷相对较小时,附着物的施加能够增强钝体的振动,提高压电俘能器的输出功率,并且最大值的出现证明实现这种增强效果的附着物存在“最优特征值”.在0.51 m/s 流速下,未包裹附着物的原始钝体对应的压电俘能器RMS 输出功率为0.83 mW,而分别应用和-2 mm 特征值的椭球型与圆柱型附着物均有最大输出,分别对应于1.41 和1.31 mW,相比于原始俘能器分别提高了69.88%和57.83%.此外当特征值大于2 mm 后,压电俘能器的输出产生不同程度的降低,这表明较大高度的附着物会抑制钝体的振动.

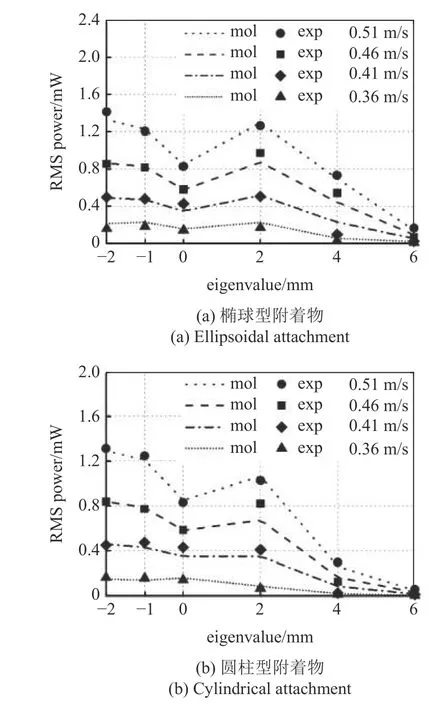
图6 不同形状附着物的压电俘能器RMS 输出功率随特征值的变化Fig.6 Variation of RMS output power for energy harvesters versus eigenvalues with different shaped attachment applied

对于圆柱型附着物如图6(b) 所示,随着附着物高度从最大凹陷增加到最大凸起,压电俘能器的RMS 输出功率在Ecy＜ 0 的范围内不断降低,并在E=0 处达到极小值;而在Ecy＞ 0 时又呈现先增大后减小的趋势.这与椭球型附着物的趋势基本一致,说明两种形状附着物的特征值变化对压电俘能器输出的影响规律是基本相同的.

此外,附着物的恰当应用能够增加压电俘能器的输出.在椭球型附着物特征值为-2 mm、流速为0.51 m/s 的条件下,俘能器的最大RMS 输出功率为1.411 mW,对应的输出功率密度ρp可被计算为11998.3 W/m3,与部分研究的俘能器输出功率密度对比如表2 所示.

表2 与同类研究对比Table 2 Comparison with similar studies

4.3 特征值对悬臂梁振幅影响的分析

为了进一步分析附着物特征值的变化对压电俘能器输出的影响,通过机电解耦得到悬臂梁的底端振幅,如图7 所示.通过与图6 中相应特征值条件下RMS 输出功率的对比可以发现,悬臂梁的振幅与压电俘能器输出功率的变化趋势基本相同,二者呈正相关.此外当U=0.51 m/s 时,没有施加附着物的悬臂梁振幅为20.25 mm,相同流速下钝体包裹了Ecy=6 mm 附着物的悬臂梁振幅则为3.07 mm,降低了84.83%,此时悬臂梁几乎静止,钝体的振动得到大幅度抑制.

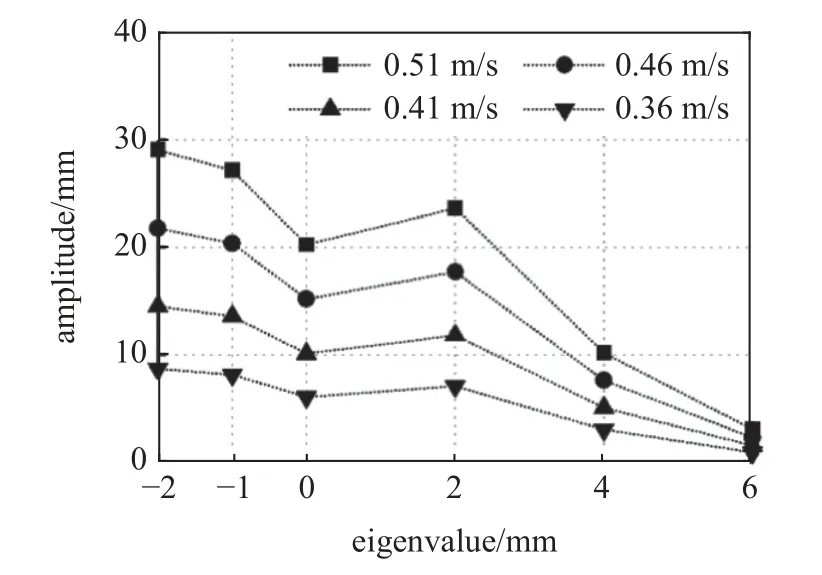
图7 圆柱型附着物悬臂梁的振幅随特征值的变化Fig.7 Variation of amplitude with eigenvalue of cantilever beam for cylindrical attachment

4.4 包裹附着物的钝体扰流数值模拟

适当特征值的附着物对压电俘能器功率输出具有增幅效应,并且无论是椭球型还是圆柱型附着物,凹陷或者凸起高度为2 mm 时,增幅效应均最大.因此选取Eell=-2 mm,Ecy=-2 mm,Eell=2 mm,Ecy=2 mm 和E=0 的5 个钝体进行三维数值模拟研究.D为钝体的迎水面宽度,计算域设置为20D×6D×2D,钝体距上游面6D.围绕钝体的周围设置加密的四面体网格,其他区域采用六面体网格.对网格进行无关性验证,均衡了效率和精度,最终网格数目控制在60 万左右,整体网格质量控制在0.5 以上.为了定性地研究附着物对钝体流致振动的影响,并考虑到计算效率及收敛性,将整个计算域的网格设为固定网格,湍流模型采用SSTk-ω,设置0.51 m/s 流速入口和环境出口,模拟时间步长为0.00125 s,计算步数为8000 步.

图8 绘制了5 个钝体的压力和涡量云图,从左侧流入的水流在受到钝体阻碍后流速降低并在其上游形成高压区;随后从侧边绕过加速流向下游并产生低压区,加速过程中水流受黏性的影响形成脱落涡.对比图8(a) 所示的压力云图发现: 包裹附着物的钝体周围产生的高、低压区之间的压力差明显大于未包裹附着物情况,这也对应更大的升力系数,如表3所示.图8(b) 所示的三维涡量云图也表明包裹附着物后,从钝体两侧脱落的尾涡明显更大.绝对值为2 mm 附着物的存在,使在钝体上形成的压差升高,加剧流致振动,最终提高了压电俘能器的输出,这与试验及模型得出的结果是一致的.

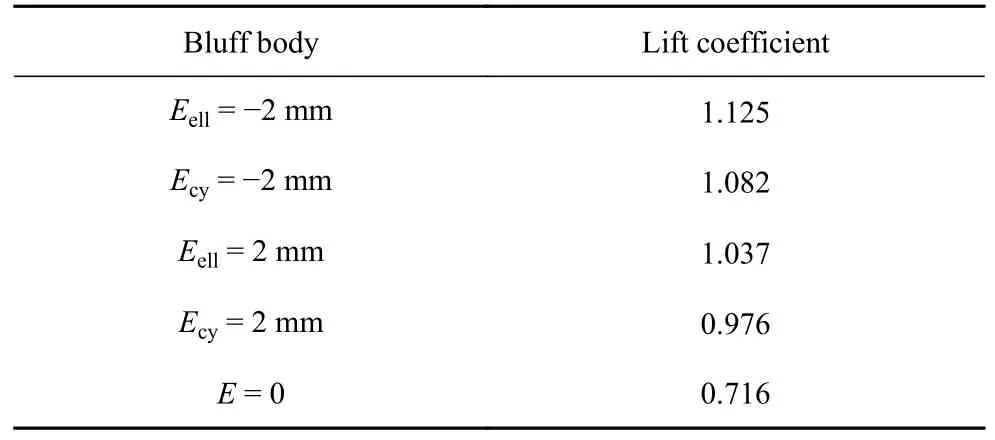
表3 升力系数Table 3 Lift coefficient

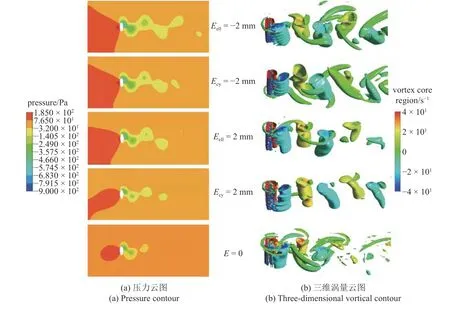
图8 U=0.51 m/s 时,Eell=2,-2 mm,Ecy=2,-2 mm 和E=0 的云图Fig.8 Contour of Eell=2,-2 mm,Ecy=2,-2 mm and E=0 with U=0.51 m/s

此外进一步对比包裹两种类型附着物钝体的脱落尾涡,发现在相同特征值下,包裹椭球型附着物的钝体尾流涡街要比包裹圆柱型附着物的情况略微紊乱,推测是因为附着物的结构干扰了流体分层,这种干扰作用在椭球型附着物上要大于圆柱型附着物.

5 总结

本文采用数学模型、实验及数值模拟相结合的方式研究了附着物的形状和附着物的特征值对驰振式压电俘能器输出的影响.基于拓展的哈密顿原理建立压电俘能器的机械控制方程,利用高斯定理建立电场-位移控制方程,通过准稳态假设计算出驰振力,在利用伽辽金法离散悬臂梁位移的基础上,实现对机电耦合控制模型的化简和解耦,最终得到系统输出及悬臂梁振动位移的近似解.模型计算的准确性得到了水槽实验的验证.利用数值模拟研究进一步分析了附着物在钝体的振动过程中发挥的作用.本文主要结论如下.

(1) 在U=0.51 m/s 和Eell=-2 mm 的条件下,压电俘能器最大RMS 输出功率为1.411 mW,相比于E=0 的情况增加了69.88%.

(2) 随着附着物的特征值从-2 mm 增加到6 mm,压电俘能器的输出功率均出现先减小再增大后减小的趋势,凸起和凹陷分别在-2 和 2 mm 取得最大值.对于增强压电俘能器的输出而言,附着物的凸起和凹陷分别存在“最优特征值”.

(3) 当U=0.51 m/s 时,Ecy=6 mm 条件下悬臂梁末端振幅为3.07 mm,与E=0 的情况相比降低了84.83%,附着物的减振效果为大跨度柔性结构的减振提供了参考.

(4) 数值模拟的结果表明: 特征值绝对值为2 mm 的附着物能够令在钝体上形成的压差升高、升力变大,引起钝体愈发剧烈的流致振动;并且附着物的应用会干扰钝体两侧的流体分层,进而对脱落尾涡的大小产生影响.