先导式电液比例阀的特性研究

邵明玺 张秀梅 黄宗经

摘要：液压阀是控制液流的压力、流量和方向的控制元件。目前在液压领域的流量控制阀主要原理是采用阀芯运动改变节流面积进而改变流量的。基于先导式溢流阀的原理，设计一款先导阀芯与主阀芯同轴配合的液压阀，提出基于CFD仿真的液压阀流量性能控制设计方法，比较主阀芯的结构形式。建立基于先导式电液比例阀结构的数学模型，并利用MATLAB进行建模仿真分析。为验证阀的动、静态流量性能，建立MATLAB模型，确定阀芯的面积—位移特性实现比例流量控制，并在试验台进行试验，验证其静态和动态流量性能。结果显示，采用矩形空心缓冲头阀芯具有良好的小流量比例特性，电液比例阀电压与流量的曲线线性度系数为0.983，流量的动态阶跃效应超调量为7%，调整时间为 0.02s。

关键词：液压机；先导阀；MATLAB仿真模型；电液比例阀；数学模型

中图分类号：S225.5

文献标识码：A

文章编号：20955553 （2023） 070131

09

Study on characteristics of pilot-operated electro-hydraulic proportional valve

Shao Mingxi， Zhang Xiumei， Huang Zongjing

（Weifang University of Science and Technology， Shouguang， 262700， China）

Abstract：  A hydraulic valve is a control element that controls the pressure， flow， and direction of the fluid flow. At present， the main principle of the flow control valve in the hydraulic field is to change the throttling area and then change the flow using the spool movement. Based on the principle of a pilot relief valve， a hydraulic valve with a coaxial pilot spool and main spool was designed. The design method of flow performance control for the hydraulic valve based on CFD simulation was proposed， and different structures of the main spool were compared. A mathematical model based on the structure of the pilot electro-hydraulic proportional valve was established and simulated with MATLAB. In order to verify the dynamic and static flow performance of the valve， a MATLAB model was established to determine the area-displacement characteristics of the valve core to achieve proportional flow control. Experiments were carried out on a test bench to verify the static and dynamic flow performance. The results show that the valve core with a rectangular hollow buffer head has good small flow ratio characteristics. The curve linearity coefficient between voltage and flow of the electro-hydraulic proportional valve was 0.983， the dynamic step effect overshoot of flow was 7%， and the adjustment time was 0.02s.

Keywords： hydraulic press; pilot valve; MATLAB simulation model; electro-hydraulic proportional valve; mathematical model

0 引言

隨着中国农业机械化水平的不断提高，高端农业机械逐渐向智能化、大型化方向发展［1］，液压系统以其调速范围广、低速稳定性好、布局方便等优点得到了广泛的应用［2］。电液比例阀作为液压系统的关键零部件，对拖拉机液压系统的稳定工作提供了重要保障。

拖拉机田间作业环境复杂多变，负载波动大，对液压系统中的元器件性能提出了较高的要求。在液压系统中，流量阀通过改变节流口开度来调节通过的流量，以此实现对系统负载流量的控制，将节流阀安装到油路上，调节执行元件的速度［3］。电液比例阀根据输入信号成比例的调节节流阀口面积进而调节流量，在液压系统中，比例阀决定系统的调速性能或动态响应速度［4］。电液比例螺纹插装阀因为其特殊性存在高可靠性、零泄漏、快速开启等性能，是流量阀研究领域中结构复杂、技术含量要求较高的种类［5］。目前，国际上两位两通液压阀种类繁多，但基本都是单阀芯结构，零位有泄漏，只能依靠电磁力驱动阀芯运动［6］。

本文以电液比例阀为研究对象，设计了一种先导阀芯与主阀芯同轴装配的先导式电液比例阀，该阀以后电磁力驱动先导阀芯，主阀芯依靠液压油压力驱动，从而实现对液压油路的节流调速功能。综合其结构特点和工作原理，建立了阀的非线性数学模型，并对其进行了仿真和试验研究。

1 节流面积特性

1.1 主阀芯结构形式

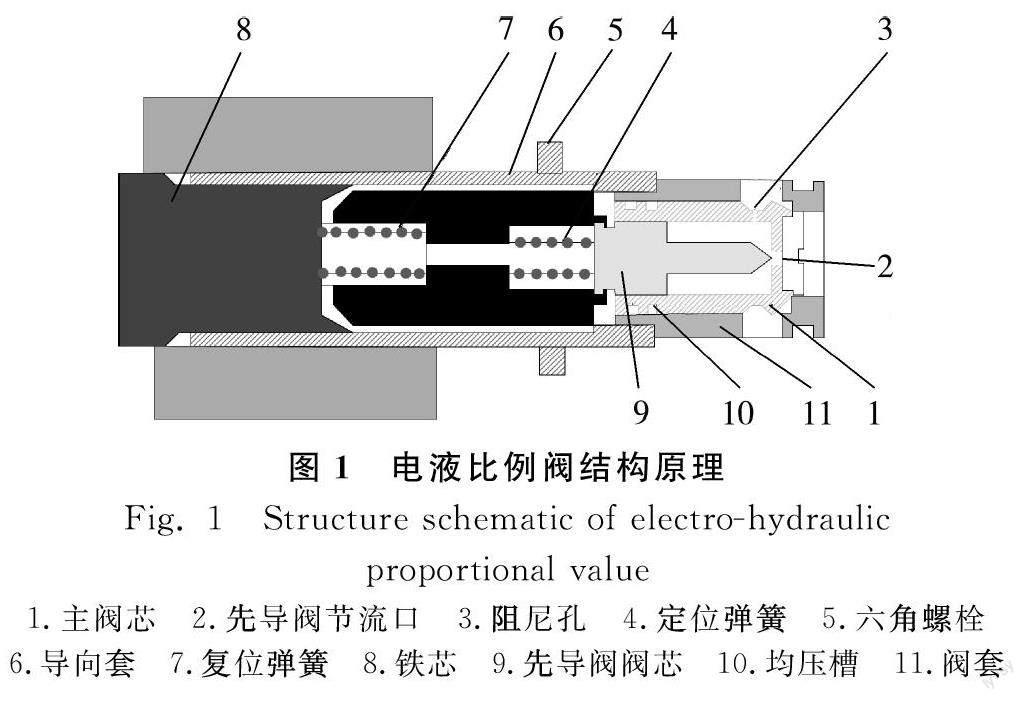
电液比例阀性能优越，广泛应用于航空航天、车辆、大型工程机械装备、农机装备等众多方向与领域。电液比例阀结构原理图如图1所示，主要由铁芯、导向套、复位弹簧、六角螺栓、定位弹簧、先导阀阀芯、均压槽、阀套、主阀芯等组成。负载压力油经主阀芯上的进油道阻尼孔流入先导阀腔，先导阀为锥阀起到自密封作用，当衔铁所受电磁力小于主弹簧的预紧力时，先导阀芯锥面与主阀上先导阀出油口贴合，此时，先导阀腔与主阀阀腔压力均与供油压力平衡，主阀阀芯没有移动，主阀节流口处于关闭状态。线圈通电，当衔铁所受的电磁力大于主弹簧预紧力与主阀芯、先导阀芯的粘性阻尼力之和时，电磁力驱动先导阀运动，主阀中心的节流口打开，油液流出，由于阻尼孔的节流作用，先导阀腔内得不到油液的及时补充，先导阀阀腔内部压力下降，小于主阀锥面承受的供油压力，主阀受到液动力驱动，主阀开启。

设计3种典型结构特征的主阀结构如图2所示，分别为无缓冲头锥阀芯、空心缓冲头、实心缓冲头结构。缓冲头节流口采用键槽铣刀加工空心缓冲头以及电火花加工矩形节流口。阀芯台肩采用数控车床加工外加磨床精加工。为了便于比较，图2（b）、图2（c）设计的圆柱缓冲头节流口沿轴向的特征长度（L均为0.8mm），负开口为0.2mm，为减少阀芯径向不平衡力对试验的影响，阀芯上沿轴向对称加工有4个均压槽，图2（a）采用无缓冲头的锥阀端面形式。

1.2 压力分布特性

液压阀对于流量的调节是通过阀芯运动改变开口度进而改变节流口面积梯度来实现，因此，研究节流口的节流面积与阀芯位移或者阀口开度的函数关系是节流阀稳态研究的重要内容［7］。一般的圆柱滑阀的面积梯度就是阀芯的周长，但本设计采用的是一种滑锥阀的形式，其面积梯度构成较为复杂。本研究针对多个开口的圆柱面缓冲头，其面积梯度较为复杂。当液压油流经节流面时，由伯努利方程可知，流速急剧上升，并且伴随压力下降，因此节流口前后压差变化很大，属于压力集中分布区域。节流面通常位于节流口后会形成一个收缩界面，对于圆孔收缩界面一般位于d/2处，然后扩散。对于本研究的矩形开口，其收缩界面只能从阀口压力分布特性入手，采用模拟分析阀口处的压降分布，进而推断收缩面的所在。应用Fluent的四面体网格对节流口抽取的流道进行网格划分，节流口进出边界做加密处理［8］。

选择K-ε湍流模型，边界条件设定为进口压力0.55MPa，出口压力因为连接油箱设定为0MPa，求解精度10-3，选取液压油密度800kg/m3，参考温度300K时的动力粘度μ为0.036kg /（m·s） 选取阀口开度过程中5个位置（Xz=0.2、0.4、0.6、0.7、1.0mm） 为分析对象，图3为对应位置处节流口对称面上的压力分布云图。

通过CFD分析可知，带空心缓冲头的阀芯，压力开始集中在入口一侧，随着阀口开启，压力开始缓冲头内部慢慢变大。实心缓冲头由于进口节流和端面小孔的节流作用，相当于半桥式液阻，两次节流，造成压差两次变化，压力从开口逐渐转移到端面不变节流口。无缓冲头压力分布从一开始节流口打开便充满流道，前后压差可调范围小，不能满足拖拉机调节量程需要。带空心缓冲头的主阀结构能够有效地降低压力的冲击，主阀芯承受对称压力，不容易发生偏移卡死现象［18］。

1.3 閥口开度与流量系数的关系分析

节流口系数与阀口开度的关系函数液压阀节流口的流动属于湍流，流量和压差的大小有关，节流口公式如式（1）所示。

Q=CdAz（Xz）2ΔPρ

（1）

经过转换可以得到开口位移与流量系数的函数关系如式（2）所示。

Cd（Xz）=QAz（Xz）ρ2ΔP

（2）

式中：

Q——主阀节流口流量，L/min；

Az——

电液比例阀主阀阀口通流面积，m2；

Xz——

电液比例阀主阀阀芯开口度，m；

Cd——阀口流量系数；

ΔP——节流口进出口压差，MP；

ρ——液压油的密度，kg/m3。

在1.2节的分析中，根据边界条件（进出口压差）计算出三种阀芯不同开口度下的流量，代入式（2）求解流量系数。三种主阀阀芯在不同开度下的流量系数如图4所示。

1） Cd1为空心缓冲头主阀阀芯结构，其流量系数随着阀口位移的增大，在Xz从0.2到0.6过程是逐渐减小（0.73～0.70），在全周开口打开之前（即1>Xz>0.8）此时有短暂上升，在Xz>1.0之后，主阀阀芯处于全周开口，此时从0.74下降到0.66。整体变化幅度不超过0.07，这个数量级在实际工程中可以认为不变，作为常数。

2） Cd2为实心缓冲头主阀阀芯结构，流量系数整体较低，可见液阻较大，Xz在刚开启一直到0.7mm处，流量系数一直减小，从0.73一直降低到0.53，这个变化范围时Cd1的接近三倍，证明此种阀芯结构流量系数不稳定。

3） Cd3为无缓冲头的主阀阀芯结构，从阀口开启到全周开口，此时流量系数一直降低，从0.92降低到0.66，波动范围较大，Cd3的平均值要高于Cd1，这种结构的通流特性优于上述两种结构。

通过图4分析，在三种不同结构的主阀芯构成的节流方案下，只有Cd1的变化范围最小，最稳定，因此选择带缓冲头的主阀阀芯结构最好。

1.4 节流口面积解析

节流口面积的计算就是首先计算面积梯度，然后将面积写成开口度的函数。对于二级节流的等效面积就是利用串联效应即半桥回路的简化，等效为一个面积，然后假设压差完全作用在这个等效面积上。实心缓冲头的节流面积即可按照这样处理［16］。

1） 空心缓冲头节流面积公式

Az=

0，0≤Xz≤Xz0

ωz（Xz-Xz0），0≤Xz-Xz0≤Xz1

ωzXz1+πd2（Xz-Xz0-Xz1）

（3）

式中：

Az——

电液比例阀控制阀主阀阀口通流面积，m2；

Xz0——

电液比例阀主阀阀芯缓冲头上负开口即不灵敏区（一般为工艺尺寸），m；

Xz1——

电液比例阀主阀缓冲头矩形开窗的最大开口度，m；

d2——电液比例阀主阀阀孔直径，m；

ρ——

液压油的密度，取ρ=900kg/m3;

ωz——

小矩形开口的面积梯度，m。

空心缓冲头节流面积如图5所示。

面积梯度

ωz=nS=nd2arcsin（L/d2）

（4）

式中：

n——

比例阀主阀芯缓冲头上矩形节流口数量；

L——矩形节流口的宽度，m；

S——矩形开口对应的圆柱面弧度，m。

2） 实心缓冲头节流口面积。

实心缓冲头由于二级节流，一级节流口节流面积与空心缓冲头计算一样，二级节流口是面积不随开度变化的，计算如下［9］

A=arcsin（L/R）β=arcsin（L/r）

（5）

h2=R2+r2-2Rrcos（β-α）

（6）

A2=hL+αR2-LRcosα2-βr2-Lrcosβ2

（7）

式中：

α——矩形开口对应内圆弧角度，rad；

β——矩形开口对应外圆弧角度，rad；

r——缓冲头内圆心半径，m；

h——为缓冲头厚度，m；

A2——为二级节流口面积，m2；

R——主阀缓冲头外圆半径，m;

ALMV——主阀阀芯全开时二级节流面积，m2。

求得A2=4×1.131mm2=4.524mm2

等效節流面积

A=11A22+1ALMV2

（8）

3） 无缓冲头的节流面积计算

A=πdMVxLMV

（9）

式中：

dMV——阀芯直径，m；

xLMV——阀芯位移，m。

无缓冲头的座阀其开口面积与普通滑阀节流面积计算方法一致即阀芯的端面面积梯度与开口量的乘积［17］。

4） MATLAB仿真。

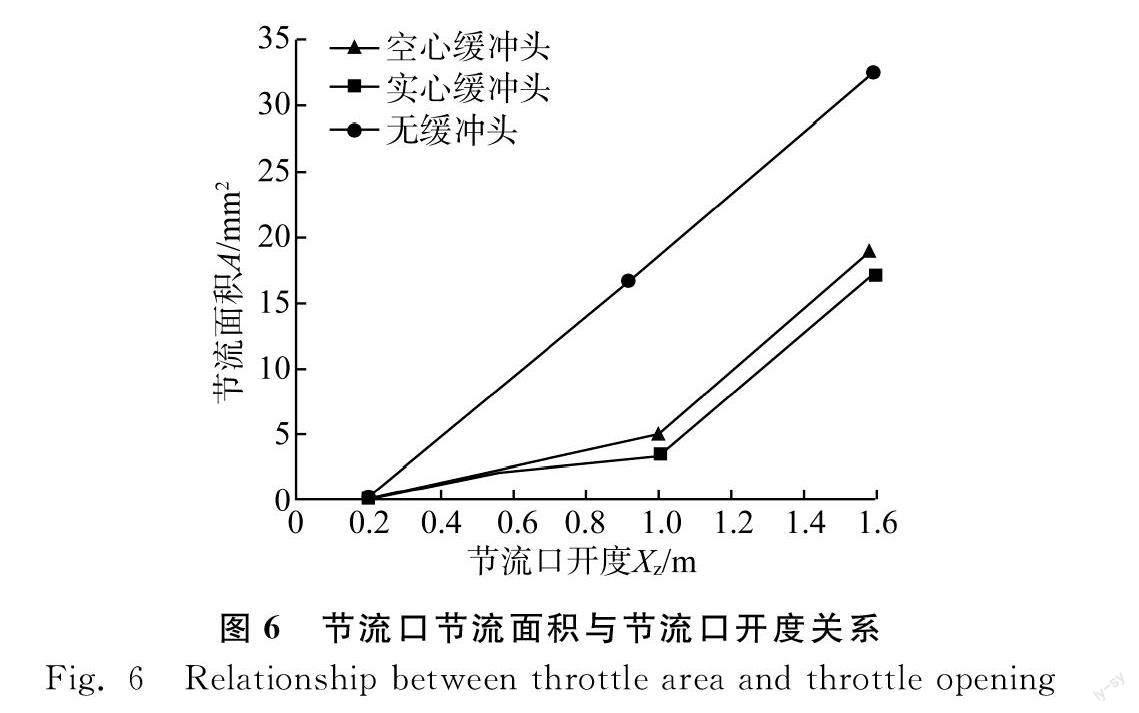
根据式（3）～式（9）采用MATLAB编制三种节流口面积计算程序，X轴为开度，Y轴为节流口面积，如图5所示：可以看出无缓冲头阀芯节流面积在经过负开口之后节流口开度和节流面积呈比例增长，一直到最大开口面积。带空心缓冲头的阀芯节流面积，在经过负开口之后缓慢增长到全开口此时最大节流面积为四个矩形节流口面积，在开口量位移到达1mm之后，处于全开口，节流面积是四个矩形开窗面积加上全周开口的面积，即图中所示的转折点之后，斜率开始变大。实心缓冲头由于缓冲头为实心，在阀芯上形成二级节流，即阀芯上四个矩形开窗有节流作用之外在阀芯端面上也有四个节流口，所以需要进行面积等效换算其面积开口度关系如图6所示。

电液比例阀的控制性能在拖拉机上的应用是后悬挂下降系统上，在下降过程中，拖拉机的负载压力作为输入压力，为了保证下降的平稳性，采用带缓冲头的设计结构，此种结构在开启时候的节流面积变化较小，因此缓慢下降，符合工况需求。同时，前后压差较大，增加缓冲头可以减小液压冲击［15］。

综上所述，通过考虑节流系数，节流面积因素，综合山地丘陵拖拉机的工况，确定选取带缓冲头的主阀阀芯结构。

2 电液比例阀数学模型的建立

确定主阀芯设计方案之后，依据先导式电液比例阀结构进行数学模型搭建，并完成仿真计算。

2.1 压差—流量特性方程

主阀节流口是薄壁小孔，符合小孔节流原理，采用小孔节流公式

Q5=Cd1Az（Xz）2（P1-P0）ρ

（10）

式中：

Q5——

经过主阀节流口进入油箱的流量，m3/s；

P1——连接液压缸的压力；

P0——油箱压力。

比例阀主阀阀芯上阻尼孔属于细长孔，因此，压力—流量方程为

Q6=πd64124μl（P1-P3）

（11）

式中：

Q6——

经过主阀阀芯阻尼孔进入先导阀阀腔的流量，m3/s；

d6——

阻尼孔直径，联通先导阀阀腔与外部液压缸；

P1——连接液压缸的压力；

P3——先导阀阀腔内部压力；

μ——液压油粘度系数，Pa·s。

l——阻尼孔长度，m。

先导阀阀口属于短孔，压力—流量方程

Q4=Cd4Ax（Xx）2P3ρ

（12）

Ax（Xx）≈πd4（Xx-Xz）sinθx

（13）

式中：

Q4——

比例阀先导阀节流口流量，m3/s；

Cd4——

先导阀阀口流量系数。

因为先导阀与主阀阀芯上的先导阀节流口属于锥阀形式。

因此，对于无倒角的锥阀阀口Cd4可表示为

Cd4≈0.18+543512≈0.76

（14）

式中：

Ax——

比例阀先导阀节流口节流面积m2；

d4——先导阀节流口直径，m；

θx——先导阀阀芯锥度角一半，rad；

Xx——

比例先导阀阀芯位移量，向上为正，m；

Xz——

比例阀主阀阀芯位移量，向上为正，m。

2.2 流量连续方程

1） 先导阀阀腔流量连续方程。先导阀启动，阻尼孔油液流入先导阀阀腔，先导阀节流口打开，油液经过先导阀节流口流出，阻尼孔流入阀腔的油液，一部分补偿被压缩量，一部分经过先导阀节流口流出，还有一部分补偿先导阀和主阀阀芯运动过程导致的先导阀阀腔容积的变化量［14］。连续性方程如式（15）所示。

Qxr-Qxc=

Vxv0-πd424Xx-π（d32-d42）4Xzβe

P·3-

πd424X·x-π（d32-d42）4X·z

（15）

式中：

βe——

液压油的体积弹性模量，βe=900×106 Pa；

d3——主阀阀芯直径，m；

d4——先导阀节流孔直径，m；

Qxr——

流经阻尼孔流入先导阀阀腔流量，m3/s;

Qxc——

先导阀阀腔流出流量，m3/s；

Vxv0——

先导阀关闭时候，先导阀阀腔的油液容积，m3。

2） 下降阀总体流量方程。

经过阀套六个圆孔流入阀内的流量，除了补偿主阀阀芯运动引起的主阀阀腔容积变化外，一部分经过主阀节流口流出，一部分经过阻尼孔进入先导阀阀腔［16］。

Q1=Q5+Q6+π（d32-d22）4X·z

（16）

式中：

Q1——比例阀进油口流入阀内部总流量，m3/s。

2.3 阀芯受力方程

1） 电液比例阀先导阀阀芯受力方程。

电液比例下降閥先导阀的受力分析：阀芯受到的外力液压油的压力、电磁铁产生的电磁力。上述两个力的合力，促使阀芯产生位移，这时候阀芯受到阻尼力（与速度有关）、弹簧力、稳态液动力、瞬态液动力、干摩擦力等［19］。但由于瞬态液动力非常小，可以忽略不计。同样，由于先导阀阀芯开了两条均压槽，因此，没有液压卡紧力，摩擦力也很小，可以忽略不计，如图7所示。

根据牛顿第二定律，在垂直方向上建立先导阀阀芯受力方程

Fxd-πd424P3=

mxdX··x+BxdX·x+Bxzd（X·x-X·z）+Kxd（Xx+Xx0）+Fxws

Xx-Xz>0&&Xx

（17）

式中：

Fxd——先导阀阀芯受到的电磁力，N。

Fxd=（u-kvX·x）kf

式中：

u——比例线圈驱动电压，V；

kf——线圈驱动系数，N/V；

kv——反电势系数，V/（m/s）；

mxd——

先导阀阀芯与铁芯加弹簧的质量，kg；

Bxd——

电磁阀衔铁运动阻尼系数，N·s/m。

Bxd=πμdtxltxδtx

式中：

μ——

液压油粘度系数，μ=4.14×10-2 Pa·s；

dtx——

电液比例阀衔铁（电磁铁芯）的直径，m；

ltx——衔铁的导向长度，m；

δtx——

衔铁与导向孔径向配合间隙，m；

Bxzd——

比例阀中先导阀阀芯与主阀相对运动的粘性阻尼系数，N·s/m。

Bxzd

=πμdxdlxdδxd1-Xx-Xzlxd

=Bxzd01-Xx-Xzlxd

（18）

其中，Bxzd0=πμdxdlxdδxd

式中：

δxd——

先导阀阀芯与主阀配合导向间隙，m；

Kxd——先导阀弹簧刚度，N/m；

Xx0——弹簧的预紧长度，m；

Xxm——先导阀阀芯的最大位移量，m；

Fxws——

电液比例阀先导阀阀芯移动后，阀芯所受的稳态液动力，N；

dxd——先导阀直径，m；

lxd——先导阀长度，m。

Fws=Cd4Cv4πd4（Xx-Xz）sin（2θx）P3

（19）

式中：

Fws——主阀阀芯所受稳态液动力，N；

Cv4——

比例阀先导阀节流口的流速系数，Cv4≈0.980。

2） 主阀阀芯受力方程。

比例阀主阀阀芯受力包括：油液压力、惯性力（假想力）、粘性阻尼力、弹簧力、稳态液动力、瞬态液动力（忽略不计）、摩擦力（忽略不计）等，如图8所示［12］。

根据牛顿第二定律，主阀阀芯的受力方程如式（20）所示。

π（d32-d22）4P1-π（d32-d42）4P3=mzfX··z+

BzfX·z+Bzfx（X·z-X·x）+Fzws

（0≤Xz≤Xzm）&&（Xx>Xz）

（20）

式中：

Xzm——比例阀主阀芯最大开口度，m；

Bzf——

比例阀主阀芯运动粘度系数，N·s/m；

Fzws——

比例阀主阀芯所受的稳态液动力，N；

mzf——主阀质量，kg;

Bzfx——先导阀运动粘度系数，N·s/m。

3 MATLAB/Simulink仿真建模

MATLAB/Simulink模型库下的用户自定义函数具有编程灵活、结构层次清晰、运行效率高等优点，适用于复杂液压系统仿真分析。根据式（8）～式（15）可得电液比例阀的状态方程［10］，应用 MATLAB 的 Function 自定义函数模块针对每一个状态量的微分方程进行了模块化处理，并根据各个状态量之间的相互作用关系建立了比例阀仿真模型，由比例下降控制阀的实际工况可知，其进出口压差由负载压力和回油压力共同决定，在悬挂农具平稳下降过程中，近似恒定［11］，因此流经比例下降控制阀的流量仅由主阀芯位移量决定。基于所建立的比例下降控制阀仿真模型，在给定负载压力0.55MPa不变的情况下，将比例电磁线圈驱动电压作为输入，将比例下降控制阀流量作为输出，得到比例下降控制阀在不同驱动电压下的稳态流量曲线如图9所示。

电压由2.5V上升至5V时，在0.55MPa的压差下，通过阀门的流量由0上升到22L/min左右。山地丘陵拖拉机设计最大流量为20L/min，误差百分之五左右，满足设计要求。

由图10可知，给定电压4V，在3s时，负载压力由0.3MPa节约到0.5MPa，流量由11.5L/min阶跃到14.2L/min。电压给定电压比例阀主阀节流口位移固定，进行压力阶跃动态仿真，比较阀腔内部压力变化以及流量变化。

由图11可知，负载压力由0.3MPa阶跃变化到0.5MPa时，系统压力响应时间约为0.02s，超调量约为34%；负载阶跃时，流量快速调整到14.2L/min左右，调整时间约为0.02s，超调量7.3%。

4 试验与分析

4.1 电液比例插装试验测试平台搭建

电液比例阀加工完成后，搭建测试平台测试其性能。试验平台主要有液压泵（定量泵）、液压管路、管接头、控制器、信号发生器、压力表、流量表、信号采集器、计算机组成。

4.2 试验方法

依据搭建的试验台，将螺纹插装阀安装到集成块，进行液压阀的稳态特性验证。稳态流量特性是指在负载压力保持不变情况下，改变控制电压得到的阀口出口流量与电压的线性关系。

图12是电液比例阀液压测试回路的试验方案原理图。在液压泵站中溢流节流阀用来调节定量泵出口处流量，溢流阀防止液压系统过载，开启压力为16MPa，比例溢流阀与现有液压回路串联（并联），用来模拟该液压回路工作时，液压缸产生的负载压力。其中，比例溢流阀开启压力、电液比例阀阀芯位移通过制器进行实时控制。

4.3 结果与分析

4.3.1 稳态试验结果分析

通过控制器调节溢流阀的开启压力，使阀的负载压力与回油压力之间的压差稳定在0.55MPa，改变阀的驱动电压，得到电液比例阀的稳态流量曲线，试验数据经线性拟合后得到电液比例阀的稳态流量特性曲线，如图13所示。

由图13可知，试验得到稳态流量特性曲线与仿真得到的静态流量特性曲线大致相同。死区电压大约为2.6V，受定量泵最大输出流量的限制，阀最大流量能达到25L/min左右，阀的稳态流量回程误差大约为9%，满足悬挂机构对阀的功能需求。

4.3.2 动态试验结果分析

1） 下降阀控制电压保持不变，负载阶跃变化时液压系统动态响应特性。

设定下降阀控制电压为3.2V，由控制器控制比例溢流阀的开启压力在2.5～4MPa之间以30s为周期进行阶跃变化，得到下降阀流量和压力动态响应特性曲线，如图14所示。

由图14可知，下降阀的负载压力在2.5～4MPa之间阶跃变化时，系统的建压和卸压时间均小于1s，负载超调量约小于1%，流经下降阀的流量几乎不受负载阶跃变化的影响。

2） 下降阀负载压力保持不变，控制电压阶跃变化时液压系统动态响应特性。

通过控制器设定比例溢流阀的开启压力为2MPa，下降阀控制电压由3.0～3.2V以30s为周期阶跃变化，得到下降阀流量和压力的动态响应特性曲线，如图15所示。

由圖15可知，在下降阀控制电压阶跃变化时，负载压力几乎保持不变，系统流量受控制电压阶跃变化的影响，在7～9.5L/min之间阶跃变化，与仿真结果基本一致。系统流量的响应时间大约为5s，超调量小于1%，符合拖拉机液压系统的设计要求。

5 结论

1） 基于液阻原理，从压降分布特性入手，采用CFD仿真方法定性的分析阀芯不同开口度的压力分布，根据流量系数的变化特性，设计了三种主阀芯结构。通过对比三种不同阀芯结构的节流面积特性，发现空心缓冲头型主阀阀芯结构下的流量系数的变化范围最小且最稳定，综合考虑节流系数和节流面积等因素，最终选取带缓冲头型的主阀阀芯设计结构方案。

2） 针对所设计的电液比例阀特性，进行了MATLAB仿真试验，仿真结果表明：在复合工况下，当负载压力由0.3MPa阶跃变化到0.5MPa时，系统压力响应时间约为0.02s，超调量约为34%；流量快速调整到14.2L/min左右，调整时间约为0.02s，超调量7.3%。系统响应时间和稳定性较好，阀芯结构设计合理。

3） 室内试验台试验研究，试验结果表明阀的负载压力与回油压力之间的压差稳定，驱动电压变化工况下，稳态流量回程误差大约为9%；下降阀控制电压保持不变，负载阶跃变化工况下，系统的建压和卸压时间均小于1s，负载超调量约小于1%；下降阀负载压力保持不变，控制电压阶跃变化工况下系统流量的响应时间大约为5s，超调量小于1%，符合丘陵山地拖拉机液压系统的设计要求。

参 考 文 献

［1］ 武建设， 陈学庚. 新疆兵团棉花生产机械化发展现状问题及对策［J］. 农业工程学报， 2015， 31（18）： 5-10.

Wu Jianshe， Chen Xuegeng. Present situation， problems and countermeasures of cotton production mechanization development in Xinjiang production and construction corps ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015， 31（18）： 5-10.

［2］ Nekatibeb B， Komanapalli V L N， Debebe M， et al. Modeling and control of Electro-Hydraulic actuator［C］.International Conference on Advances of Science and Technology. Springer， Cham， 2019： 332-342.

［3］ 黄雪峰. 直动式水压溢流阀压力特性研究［D］. 成都： 西南交通大学， 2009.

Huang Xuefeng. The analysis on the water direct-actuated relief valves pressure characteristic［D］. Chengdu： Southwest Jiaotong University， 2009.

［4］ 王东升. 节流槽滑阀阀口流量系数及稳态液动力计算的研究［D］. 兰州： 兰州理工大学， 2008.

Wang Dongsheng. Investigation into coefficient of orifice and calculation of steady flow force of spool valve with notches ［D］. Lanzhou： Lanzhou University of Technology， 2008.

［5］ Nahian S A， Truong D Q， Chowdhury P， et al. Modeling and fault tolerant control of an electro-hydraulic actuator ［J］. International Journal of Precision Engineering and Manufacturing， 2016， 17： 1285-1297.

［6］ 冀宏， 王东升， 刘小平， 等. 滑阀节流槽阀口的流量控制特性［J］. 农业机械学报， 2009， 40（1）： 198-202.

Ji Hong， Wang Dongsheng， Liu Xiaoping， et al. Flow control characteristic of the orifice in spool valve with notches［J］. Transactions of the Chinese Society of Agricultural Machinery， 2009， 40（1）： 198-202.

［7］ 謝斌. 拖拉机农具仿真作业机组悬挂系统电液控制技术的研究［D］. 北京： 中国农业大学， 2000.

Xie Bin. Study on electrohy-draulic control technology of hitch system for the tractor-implement combination ［D］. Beijing： China Agricultural University， 2000.

［8］ 李明生， 朱忠祥， 毛恩荣， 等. 大功率拖拉机电液提升器比例提升阀设计［J］. 农业机械学报， 2012， 43（10）： 31-35， 89.

Li Mingsheng， Zhu Zhongxiang， Mao Enrong， et al. Design of proportional raise valve in electro-hydraulic lifting mechanism of big-power tractor ［J］. Transactions of the Chinese Society of Agricultural Machinery， 2012， 43（10）： 31-35， 89.

［9］ 陈随英， 赵建军， 毛恩荣， 等. 负载敏感变量泵结构建模与性能分析［J］. 农业工程学报， 2017， 33（3）： 40-49.

Chen Suiying， Zhao Jianjun， Mao Enrong， et al. Structural modeling and performance analysis of load-sensing variable pump［J］. Transactions of the Chinese Society of Agricultural Engineering， 2017， 33（3）： 40-49.

［10］ 路甬祥， 胡大弘. 电液比例控制技术［M］. 北京： 機械工业出版社， 1988.

Lu Yongxiang， Hu Dahong. Electrohydraulic proportional control technology［M］. Beijing： China Machine Press， 1988.

［11］ 赵建军， 朱忠祥， 宋正河，等. 重型拖拉机电液悬挂比例控制器设计［J］. 农业机械学报， 2014， 45（S1）： 10-16.

Zhao Jianjun， Zhu Zhongxiang， Song Zhenghe， et al. Proportional controller for electro-hydraulic hitch system in heavy tractor ［J］. Transactions of the Chinese Society of Agricultural Machinery， 2014， 45（S1）： 10-16.

［12］ 程文祥. 拖拉机耕深微机控制系统的研究［J］. 农业机械学报， 1995（3）： 15-19.

Cheng Wenxiang. Research on the microcomputer automatic controlling ploughing depth of a tractor ［J］. Transactions of the Chinese Society of Agricultural Machinery， 1995（3）： 15-19.

［13］ 董秀林， 史维祥， 周福章， 等. 拖拉机阻力控制系统实验分析与动态性能评价指标体系探讨［J］. 农业工程学报， 1997（1）： 74-77.

Dong Xiulin， Shi Weixiang， Zhou Fuzhang， et al. Experiment research on the tractor draught control system and discussion on the judging target system ［J］. Transactions of the Chinese Society of Agricultural Engineering， 1997（1）： 74-77.

［14］ 吴国桢， 程文祥， 姚庆祥， 等. 拖拉机耕深自动监测与控制［J］. 农业机械学报， 1993（1）： 31-36.

Wu Guozhen， Cheng Wenxiang， Yao Qingxiang， et al. Research on automatic monitoring and controlling ploughing depth of a tractor ［J］. Transactions of the Chinese Society of Agricultural Machinery， 1993 （1）： 31-36.

［15］ 承鉴， 迟瑞娟， 赖青青， 等. 基于电液悬挂系统的拖拉机主动减振控制［J］. 农业工程学报， 2017， 33（5）： 82-90.

Cheng Jian， Chi Ruijuan， Lai Qingqing， et al. Active vibration control of tractor based on electro-hydraulic hitch system ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2017， 33（5）： 82-90.

［16］ 韩科立， 朱忠祥， 毛恩荣， 等. 基于最优控制的导航拖拉机速度与航向联合控制方法［J］. 农业机械学报， 2013， 44（2）： 165-170.

Han Keli， Zhu Zhongxiang， Mao Enrong， et al. Joint control method of speed and heading of navigation tractor based on optimal control ［J］. Transactions of the Chinese Society of Agricultural Machinery， 2013， 44（2）： 165-170.

［17］ 杜巧连， 熊熙程， 魏建华. 拖拉机液压悬挂耕深电液控制系统设计与试验［J］. 农业机械学报， 2008（8）： 62-65.

Du Qiaolian， Xiong Xicheng， Wei Jianhua. Design and experiment on the control system of electro-hydraulic plow depth of tractor hydraulic hitch mechanism ［J］. Transactions of the Chinese Society of Agricultural Machinery， 2008（8）： 62-65.

［18］ 吕安涛， 毛恩荣， 宋正河， 等. 一种拖拉机自动驾驶复合模糊控制方法［J］. 农业机械学报， 2006（4）： 17-20.

Lü Antao， Mao Enrong， Song Zhenghe， et al. A complex fuzzy control technique of tractor automatic steering ［J］. Transactions of the Chinese Society of Agricultural Machinery， 2006（4）： 17-20.